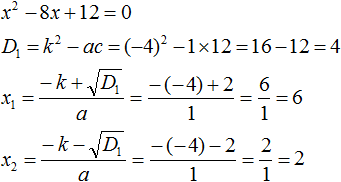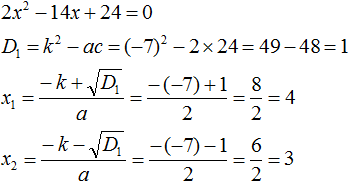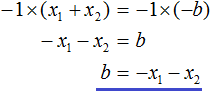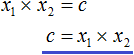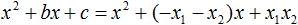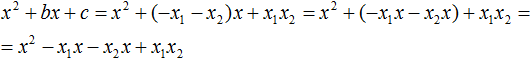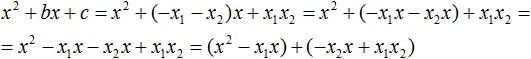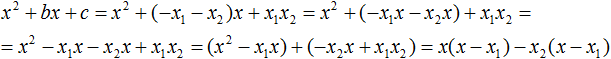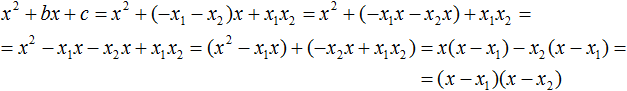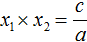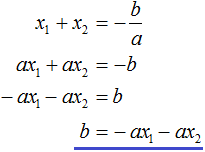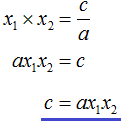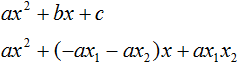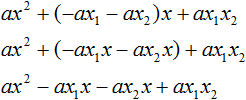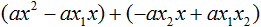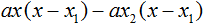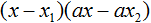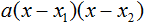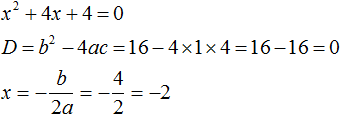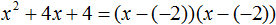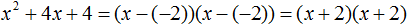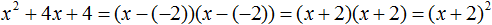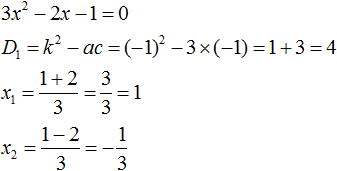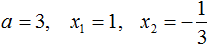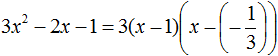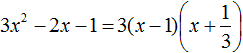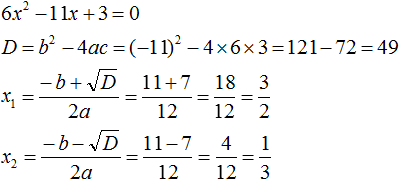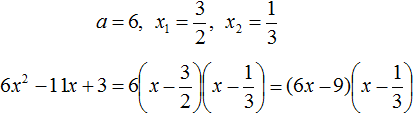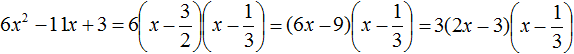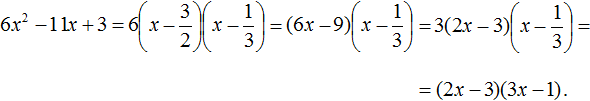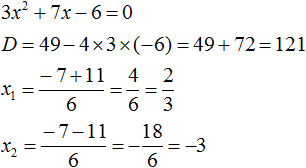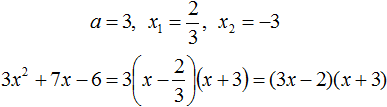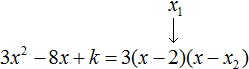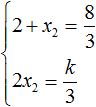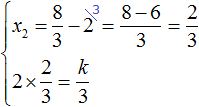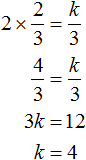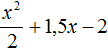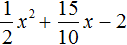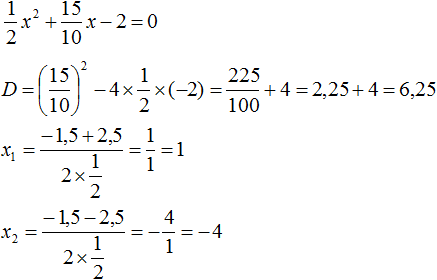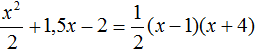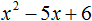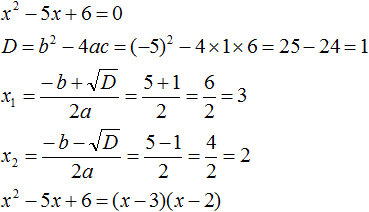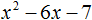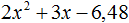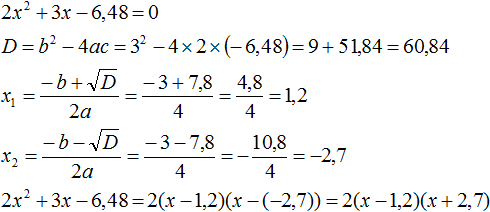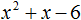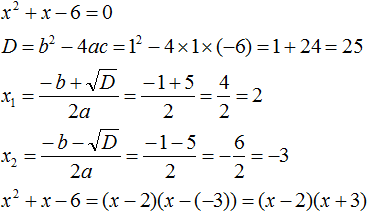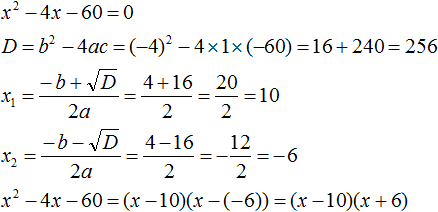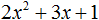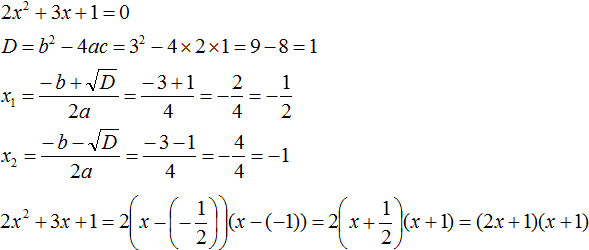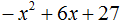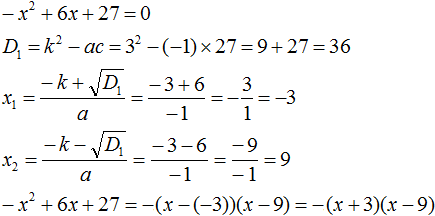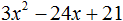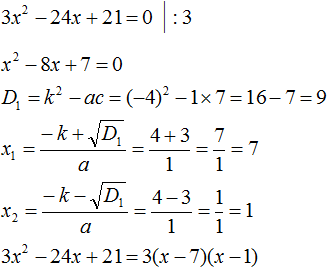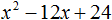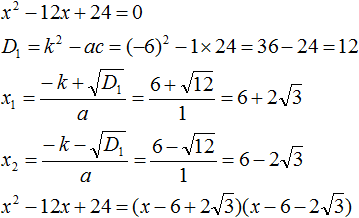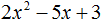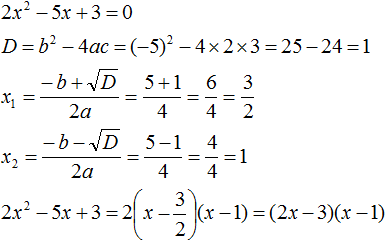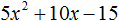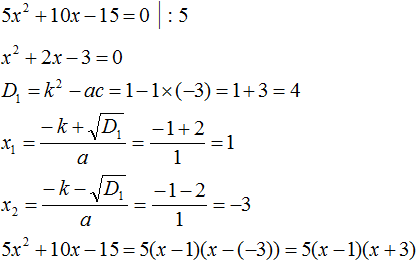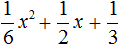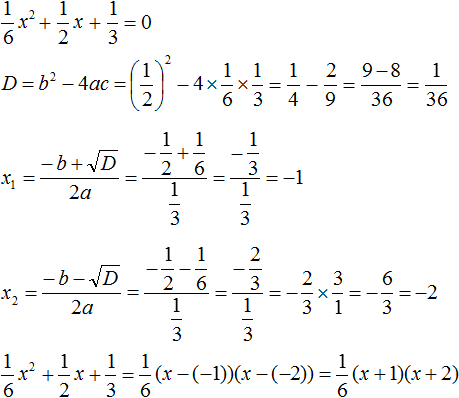Как раскладывать квадратное уравнение на две скобки

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Видео:Математика| Разложение квадратного трехчлена на множители.Скачать

Калькулятор онлайн.
Выделение квадрата двучлена и разложение на множители квадратного трехчлена.

Т.е. задачи сводятся к нахождению чисел ( p, q ) и ( n, m )

Программа не только даёт ответ задачи, но и отображает процесс решения.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Если вы не знакомы с правилами ввода квадратного трехчлена, рекомендуем с ними ознакомиться.

В качестве переменной может выступать любая латинсая буква.
Например: ( x, y, z, a, b, c, o, p, q ) и т.д.

Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.

Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5x — 3,5x^2

Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.

Знаменатель не может быть отрицательным.

При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Целая часть отделяется от дроби знаком амперсанд: &
Ввод: 3&1/3 — 5&6/5x +1/7x^2
Результат: ( 3frac — 5frac x + fracx^2 )

При вводе выражения можно использовать скобки. В этом случае при решении введённое выражение сначала упрощается.
Например: 1/2(x-1)(x+1)-(5x-10&1/2)

Видео:Квадратный Трехчлен / Разложение квадратного трехчлена на множители, Как решать Квадратные УравненияСкачать

Разложение квадратного трёхчлена на множители

Видео:Решение квадратных уравнений. Метод разложения на множители. 8 класс.Скачать

Как разложить на множители квадратный трёхчлен

Квадратный трёхчлен — это многочлен вида ax 2 + bx + c .

В прошлых уроках мы решали квадратные уравнения. Общий вид таких уравнений выглядел так:

Левая часть этого уравнения является квадратным трёхчленом.

Одним из полезных преобразований при решении задач является разложение квадратного трёхчлена на множители. Для этого исходный квадратный трёхчлен приравнивают к нулю и решают квадратное уравнение. В этом случае говорят, что выполняется поиск корней квадратного трёхчлена.

Полученные корни x₁ и x₂ следует подстáвить в следующее выражение, которое и станет разложением:

Таким образом, чтобы разложить квадратный трёхчлен на множители при помощи решения квадратного уравнения, нужно воспользоваться следующей готовой формулой:

Где левая часть — исходный квадратный трёхчлен.

Пример 1. Разложить на множители следующий квадратный трёхчлен:

Найдём корни квадратного трёхчлена. Для этого приравняем данный квадратный трёхчлен к нулю и решим квадратное уравнение:

В данном случае коэффициент b является чётным. Поэтому можно воспользоваться формулами для чётного второго коэффициента. Чтобы сэкономить время, некоторые подробные вычисления можно пропустить:

Итак, x₁ = 6 , x₂ = 2 . Теперь воспользуемся формулой ax 2 + bx + c = a(x − x₁)(x − x₂). В левой части вместо выражения ax 2 + bx + c напишем свой квадратный трёхчлен x 2 − 8x + 12. А в правой части подставим имеющиеся у нас значения. В данном случае a = 1, x₁ = 6, x₂ = 2

Если a равно единице (как в данном примере), то решение можно записать покороче:

Чтобы проверить правильно ли разложен квадратный трёхчлен на множители, нужно раскрыть скобки у правой части получившегося равенства.

Раскроем скобки у правой части равенства, то есть в выражении (x − 6)(x − 2) . Если мы всё сделали правильно, то должен получиться квадратный трёхчлен x 2 − 8x + 12

Пример 2. Разложить на множители следующий квадратный трёхчлен:

Приравняем данный квадратный трёхчлен к нулю и решим уравнение:

Как и в прошлом примере коэффициент b является чётным. Поэтому можно воспользоваться формулами для чётного второго коэффициента:

Итак, x₁ = 4 , x₂ = 3 . Приравняем квадратный трехчлен 2x 2 − 14x + 24 к выражению a(x − x₁)(x − x₂) , где вместо переменных a , x₁ и x₂ подстáвим соответствующие значения. В данном случае a = 2

Выполним проверку. Для этого раскроем скобки у правой части получившегося равенства. Если мы всё сделали правильно, то должен получиться квадратный трёхчлен 2x 2 − 14x + 24

Видео:Математика - Разложение трехчлена на множителиСкачать

Как это работает

Разложение квадратного трёхчлена на множители происходит, если вместо коэффициентов квадратного трёхчлена подстáвить теорему Виета и выполнить тождественные преобразования.

Для начала рассмотрим случай, когда коэффициент a квадратного трёхчлена равен единице:

Вспоминаем, что если квадратное уравнение является приведённым, то теорема Виета имеет вид:

Тогда приведённый квадратный трехчлен x 2 + bx + c можно разложить на множители следующим образом. Сначала выразим b из уравнения x₁ + x₂ = −b . Для этого можно умножить обе его части на −1

Переменную c из теоремы Виета выражать не нужно — она уже выражена. Достаточно поменять местами левую и правую часть:

Теперь подставим выраженные переменные b и c в квадратный трёхчлен x 2 + bx + c

Раскроем скобки там где это можно:

В получившемся выражении выполним разложение многочлена на множители способом группировки. В данном случае удобно сгруппировать первый член со вторым, а третий с четвёртым:

Из первых скобок вынесем общий множитель x , из вторых скобок — общий множитель −x₂

Далее замечаем, что выражение ( x − x₁ ) является общим множителем. Вынесем его за скобки:

Но это был случай, когда исходный квадратный трёхчлен является приведённым. В нём коэффициент a равен единице. И соответственно, в формуле разложения такого квадратного трехчлена коэффициент a можно опустить.

Теперь рассмотрим случай, когда коэффициент a квадратного трёхчлена не равен единице. Это как раз тот случай, когда в формуле разложения присутствует перед скобками коэффициент a

Вспоминаем, что если квадратное уравнение не является приведённым, то есть имеет вид ax 2 + bx + c = 0 , то теорема Виета принимает следующий вид:

Это потому что теорема Виета работает только для приведённых квадратных уравнений. А чтобы уравнение ax 2 + bx + c = 0 стало приведённым, нужно разделить обе его части на a

Далее чтобы квадратный трёхчлен вида ax 2 + bx + c разложить на множители, нужно вместо b и c подставить соответствующие выражения из теоремы Виета. Но в этот раз нам следует использовать равенства 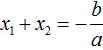и

Для начала выразим b и c . В первом равенстве умножим обе части на a . Затем обе части получившегося равенства умножим на −1

Теперь из второго равенства выразим c . Для этого умножим обе его части на a

Теперь подставим выраженные переменные b и с в квадратный трёхчлен ax 2 + bx + c . Для наглядности каждое преобразование будем выполнять на новой строчке:

Здесь вместо переменных b и c были подставлены выражения −ax₁ − ax₂ и ax₁x₂ , которые мы ранее выразили из теоремы Виета. Теперь раскроем скобки там где это можно:

В получившемся выражении выполним разложение многочлена на множители способом группировки. В данном случае удобно сгруппировать первый член со вторым, а третий с четвёртым:

Теперь из первых скобок вынесем общий множитель ax , а из вторых — общий множитель −ax₂

Далее замечаем, что выражение x − x₁ тоже является общим множителем. Вынесем его за скобки:

Вторые скобки содержат общий множитель a . Вынесем его за скобки. Его можно расположить в самом начале выражения:

Отметим, что если квадратный трехчлен не имеет корней, то его нельзя разложить на множители. Действительно, если не найдены корни квадратного трёхчлена, то нéчего будет подставлять в выражение a(x − x₁)(x − x₂) вместо переменных x₁ и x₂ .

Если квадратный трёхчлен имеет только один корень, то этот корень одновременно подставляется в x₁ и x₂ . Например, квадратный трёхчлен x 2 + 4x + 4 имеет только один корень −2

Тогда значение −2 в процессе разложения на множители будет подставлено вместо x₁ и x₂ . А значение a в данном случае равно единице. Её можно не записывать, поскольку это ничего не даст:

Скобки внутри скобок можно раскрыть. Тогда получим следующее:

При этом если нужно получить короткий ответ, последнее выражение можно записать в виде (x + 2) 2 поскольку выражение (x + 2)(x + 2) это перемножение двух сомножителей, каждый из которых равен (x + 2)

Видео:Разложение квадратного трехчлена на множители. 8 класс.Скачать

Примеры разложений

Пример 1. Разложить на множители следующий квадратный трёхчлен:

Найдём корни квадратного трёхчлена:

Воспользуемся формулой разложения. В левой части напишем квадратный трёхчлен 3x 2 − 2x − 1 , а в правой части — его разложение в виде a(x − x₁)(x − x₂) , где вместо a , x₁ и x₂ подстáвим соответствующие значения:

Во вторых скобках можно заменить вычитание сложением:

Пример 2. Разложить на множители следующий квадратный трёхчлен:

Упорядочим члены так, чтобы старший коэффициент располагался первым, средний — вторым, свободный член — третьим:

Найдём корни квадратного трёхчлена:

Воспользуемся формулой разложения:

Упростим получившееся разложение. Вынесем за первые скобки общий множитель 3

Теперь воспользуемся сочетательным законом умножения. Напомним, что он позволяет перемножать сомножители в любом порядке. Умножим 3 на вторые скобки. Это позвóлит избавиться от дроби в этих скобках:

Пример 3. Разложить на множители следующий квадратный трёхчлен:

Найдём корни квадратного трёхчлена:

Воспользуемся формулой разложения:

Пример 4. Найдите значение k , при котором разложение на множители трёхчлена 3x 2 − 8x + k содержит множитель (x − 2)

Если разложение содержит множитель (x − 2) , то один из корней квадратного трёхчлена равен 2 . Пусть корень 2 это значение переменной x₁

Чтобы найти значение k , нужно знать чему равен второй корень. Для его определения воспользуемся теоремой Виета.

В данном случае квадратный трёхчлен не является приведённым, поэтому сумма его корней будет равна дроби , а произведение корней — дроби

Выразим из первого равенства переменную x₂ и сразу подстáвим найденное значение во второе равенство вместо x₂

Теперь из второго равенства выразим k . Так мы найдём его значение.

Пример 5. Разложить на множители следующий квадратный трёхчлен:

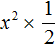
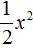
Перепишем данный трёхчлен в удобный для нас вид. Если в первом члене заменить деление умножением, то получим . Если поменять местами сомножители, то получится . То есть коэффициент a станет равным

Коэффициент b можно перевести в обыкновенную дробь. Так проще будет искать дискриминант:

Найдём корни квадратного трёхчлена:

Воспользуемся формулой разложения:

Видео:№2 Квадратное уравнение со скобками (х-1)(x-2)=-6х Как избавиться от скобок в уравнении Как решить уСкачать

Задания для самостоятельного решения

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Разложение квадратного трёхчлена на множители

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На данном уроке мы с вами научимся раскладывать квадратные трёхчлены на линейные множители. Для этого необходимо вспомнить теорему Виета и обратную ей. Данное умение поможет нам быстро и удобно раскладывать квадратные трёхчлены на линейные множители, а также упростит сокращение дробей, состоящих из выражений.

Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Упрощение выражений»

📺 Видео

Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

№5 Квадратное уравнение со скобками (5x-3)^2=(5х+13)^2 Как избавиться от скобок в уравнении Как решиСкачать

Быстрый способ решения квадратного уравненияСкачать

№4 Квадратное уравнение со скобками (2x-5)^2-4х^2=0 Как избавиться от скобок в уравнении Как решитьСкачать

Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать

№3 Квадратное уравнение со скобками x^2-9=(х+3)^2 Как избавиться от скобок в уравнении Как решить урСкачать

ОГЭ математика. Задача 9. Решаем квадратное уравнение методом разложения на множителиСкачать

Неполные квадратные уравнения. Алгебра, 8 классСкачать

№1 Квадратное уравнение со скобками (-5х+3)(-x+6)=0 Как избавиться от скобок в уравнении Как решитьСкачать

Как решать любое квадратное уравнение Полное Неполное квадр ур x^2+2x-3=0 5x^2-2x=0 2x^2-2=0 3x^2=0Скачать

№8 Неполное квадратное уравнение √26х-3x^2=0 Как разложить на множители Вынести х за скобку Как решиСкачать

Решение биквадратных уравнений. 8 класс.Скачать

№5 Неполное квадратное уравнение х^2-3x=0 Как разложить на множители Вынести х за скобку Как решитьСкачать