Как проверить перпендикулярность плоскостей по их уравнениям

Эта статья о перпендикулярных плоскостях. Сначала дано определение перпендикулярных плоскостей, показаны обозначения и приведены примеры. После этого сформулирован признак перпендикулярности плоскостей и условие перпендикулярности двух плоскостей. В заключении детально разобраны решения характерных задач.

Навигация по странице.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Перпендикулярные плоскости – основные сведения.

Определение перпендикулярных плоскостей дается через угол между пересекающимися плоскостями.

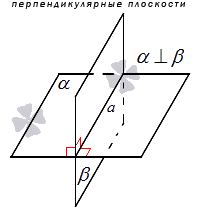
Две пересекающиеся плоскости называются перпендикулярными, если угол между ними равен девяноста градусам.

Для обозначения перпендикулярности используют символ вида «». То есть, если плоскости и перпендикулярны, то можно кратко записать .

Если плоскости и перпендикулярны, то можно также сказать, что плоскость перпендикулярна к плоскости или плоскость перпендикулярна к плоскости . Поэтому перпендикулярные плоскости и часто называют взаимно перпендикулярными.

В качестве примера перпендикулярных плоскостей можно привести плоскости стены и пола в комнате.

Видео:Перпендикулярность прямой и плоскости. 10 класс.Скачать

Перпендикулярность плоскостей – признак и условие перпендикулярности.

На практике часто приходится определять, перпендикулярны ли две заданные плоскости. Для этого можно найти угол между заданными плоскостями, и если он будет равен , то по определению плоскости будут перпендикулярными.

Также существует признак перпендикулярности двух плоскостей, который часто используется для доказательства перпендикулярности двух плоскостей. В его формулировке участвуют перпендикулярные прямая и плоскость. Сформулируем признак перпендикулярности двух плоскостей в виде теоремы.

Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то заданные плоскости перпендикулярны.

Доказательство признака перпендикулярности двух плоскостей Вы можете посмотреть в учебнике по геометрии за 10 — 11 классы.

Из этого признака напрямую следует, что если плоскость перпендикулярна к линии пересечения двух заданных плоскостей, то она перпендикулярна к каждой из этих плоскостей.

Теперь рассмотрим необходимое и достаточное условие перпендикулярности двух плоскостей, которое удобно применять для проверки перпендикулярности плоскостей, заданных в прямоугольной системе координат в трехмерном пространстве. Определение нормального вектора плоскости позволяет доказать следующее необходимое и достаточное условие перпендикулярности двух плоскостей.

Для перпендикулярности двух пересекающихся плоскостей необходимо и достаточно, чтобы нормальные векторы этих плоскостей были перпендикулярны.

Пусть в трехмерном пространстве зафиксирована прямоугольная система координат. Если и — нормальные векторы плоскостей и соответственно, то необходимое и достаточное условие перпендикулярности векторов и имеет вид . Таким образом, если и — нормальные векторы плоскостей и соответственно, то для перпендикулярности плоскостей и необходимо и достаточно, чтобы скалярное произведение векторов и равнялось нулю, то есть, чтобы выполнялось равенство .

Разберем решения нескольких примеров.

Перпендикулярны ли плоскости, заданные в прямоугольной системе координат Oxyz в трехмерном пространстве уравнениями и ?

Чтобы ответить на вопрос о перпендикулярности заданных плоскостей, найдем координаты нормальных векторов этих плоскостей и проверим выполнение условия перпендикулярности этих векторв.

Общее уравнение плоскости позволяет сразу записать координаты нормального вектора: .

Чтобы определить координаты нормального вектора плоскости , перейдем от уравнения плоскости в отрезках к общему уравнению плоскости: . Таким образом, — нормальный вектор плоскости .

Вычислим скалярное произведение векторов и : . Так как оно отлично от нуля, то векторы и не перпендикулярны, следовательно, заданные плоскости не перпендикулярны.

нет, плоскости не перпендикулярны.

В прямоугольной системе координат Oxyz в трехмерном пространстве заданы координаты четырех точек . Проверьте перпендикулярность плоскостей АВС и ABD .

Убедимся, что скалярное произведение нормальных векторов указанных плоскостей равно нулю – это будет доказательством перпендикулярности плоскостей. Для этого сначала нам нужно найти координаты нормальных векторов и плоскостей АВС и ABD соответственно.

По известным координатам точек А , В , С и D мы можем вычислить координаты векторов , и (при необходимости смотрите статью вычисление координат вектора по координатам точек его конца и начала): .

Нормальным вектором плоскости АВС является векторное произведение векторов и , а нормальным вектором плоскости ABD является векторное произведение векторов и , то есть,

Находим скалярное произведение векторов и : . Оно равно нулю, что указывает на перпендикулярность нормальных векторов плоскостей АВС и ABD . Значит, плоскости АВС и ABD также перпендикулярны.

Заметим, что можно было по координатам заданных точек получить общие уравнения плоскостей АВС и ABD (смотрите статью уравнение плоскости, проходящей через три заданные точки), из них найти координаты нормальных векторов этих плоскостей, после чего проверить выполнение условия перпендикулярности нормальных векторов плоскостей.

Видео:10. Параллельность и перпендикулярность плоскостей Решение задачСкачать

Перпендикулярные плоскости, условие перпендикулярности плоскостей

Данная статья посвящена перпендикулярным плоскостям. Будут даны определения, обозначения вместе с примерами. Будет сформулирован признак перпендикулярности плоскостей и условие, при котором он выполним. Будут рассмотрены решения подобных задач на примерах.

Видео:10 класс, 17 урок, Признак перпендикулярности прямой и плоскостиСкачать

Перпендикулярные плоскости – основные сведения

При наличии угла между пересекающимися прямыми можно говорить об определении перпендикулярных плоскостей.

При условии, что угол между перпендикулярными прямыми равен 90 градусов, их называют перпендикулярными.

Обозначение перпендикулярности принято писать знаком « ⊥ ». Если в условии дано, что плоскости α и β перпендикулярные, тогда запись принимает вид α ⊥ β . На рисунке ниже показано подробно.

Когда в улови дано, что плоскость α и β перпендикулярны, это значит, что α перпендикулярна β и наоборот. Такие плоскости называют взаимно перпендикулярными. Например, стена и потолок в комнате являются взаимно перпендикулярными, так как при пересечении дают прямой угол.

Видео:10 класс, 18 урок, Теорема о прямой, перпендикулярной к плоскостиСкачать

Перпендикулярность плоскостей – признак и условие перпендикулярности

На практике можно встретить задания, где необходимо определить перпендикулярность заданных плоскостей. Для начала нужно определить угол между ними. Если он равен 90 градусам, тогда они считаются перпендикулярными из определения.

Для доказательства перпендикулярности двух плоскостей применяют признак перпендикулярности двух плоскостей. Формулировка содержит понятия перпендикулярная прямая и плоскость. Напишем точное определение признака перпендикулярности в виде теоремы.

Если одна из двух заданных плоскостей пересекает прямую, перпендикулярную другой плоскости, то заданные плоскости перпендикулярны.

Доказательство имеется в учебнике по геометрии за 10 — 11 класс, где есть подробное описание. Из признака следует, что, если плоскость перпендикулярна линии пересечения двух заданных плоскостей, то она перпендикулярна к каждой из этих плоскостей.

Существует необходимое и достаточное условия для доказательства. Рассмотрим их для перпендикулярности двух заданных плоскостей, которое применяется в качестве проверки их перпендикулярности, находящихся в прямоугольной системе координат трехмерного пространства. Чтобы доказательство имело силу, необходимо применить определение нормального вектора плоскости, который способствует доказать необходимое и достаточное условие перпендикулярности плоскостей.

Для того, чтобы перпендикулярность пересекающихся плоскостей была явной, необходимо и достаточно, чтобы нормальные векторы заданных плоскостей пересекались под прямым углом.

Пусть в трехмерном пространстве задана прямоугольная система координат. Если имеем n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) , являющимися нормальными векторами заданных плоскостей α и β , то необходимым и достаточным условием перпендикулярности векторов n 1 → и n 2 → примет вид

n 1 → , n 2 → = 0 ⇔ A 1 · A 2 + B 1 · B 2 + C 1 · C 2 = 0

Отсюда получаем, что n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) — нормальные векторы заданных плоскостей, а для действительности перпендикулярности α и β необходимо и достаточно, чтобы скалярное произведение векторов n 1 → и n 2 → было равным нулю, а значит, принимало вид n 1 → , n 2 → = 0 ⇔ A 1 · A 2 + B 1 · B 2 + C 1 · C 2 = 0 .

Рассмотрим подробнее на примерах.

Определить перпендикулярность плоскостей, заданных в прямоугольной системе координат O x y z трехмерно пространства, заданного уравнениями x — 3 y — 4 = 0 и x 2 3 + y — 2 + z 4 5 = 1 ?

Для нахождения ответа на вопрос о перпендикулярности для начал необходимо найти координаты нормальных векторов заданных плоскостей, после чего можно будет выполнить проверку на перпендикулярность.

x — 3 y — 4 = 0 является общим уравнением плоскости, из которого можно сразу преобразовать координаты нормального вектора, равные n 1 → = ( 1 , — 3 , 0 ) .

Для определения координаты нормального вектора плоскости x 2 3 + y — 2 + z 4 5 = 1 перейдем от уравнения плоскости в отрезках к общему.

x 2 3 + y — 2 + z 4 5 ⇔ 3 2 x — 1 2 y + 5 4 z — 1 = 0

Тогда n 2 → = 3 2 , — 1 2 , 5 4 — это координаты нормального вектора плоскости x 2 3 + y — 2 + z 4 5 = 1 .

Перейдем к вычислению скалярного произведения векторов n 1 → = ( 1 , — 3 , 0 ) и n 2 → = 3 2 , — 1 2 , 5 4 .

Получим, что n 1 → , n 2 → = 1 · 3 2 + ( — 3 ) · — 1 2 + 0 · 5 4 = 3 .

Видим, что оно не равно нулю, значит, что заданные векторы не перпендикулярны. Отсюда следует, что плоскости также не перпендикулярны. Условие не выполнено.

Ответ: плоскости не перпендикулярны.

Прямоугольная система координат O x y z имеет четыре точки с координатами A — 15 4 , — 7 8 , 1 , B 17 8 , 5 16 , 0 , C 0 , 0 , 3 7 , D — 1 , 0 , 0 . Проверить, перпендикулярны ли плоскости А В С и A B D .

Для начала необходимо рассчитать скалярное произведение векторов данных плоскостей. Если оно равно нулю, только в этом случае можно считать, что они перпендикулярны. Находим координаты нормальных векторов n 1 → и n 2 → плоскостей А В С и A B D .

Из заданных координат точек вычислим координаты векторов A B → , A C → , A D → . Получаем, что:

A B → = 47 8 , 19 16 , — 1 , A C → = 15 4 , 7 8 , — 4 7 , A D → = 11 4 , 7 8 , — 1 .

Нормальный вектор плоскости А В С является векторным произведением векторов A B → и A C → , а для A B D векторное произведение A B → и A D → . Отсюда получим, что

n 1 → = A B → × A C → = i → j → k → 47 8 19 16 — 1 15 4 7 8 — 4 7 = 11 56 · i → — 11 28 · j → + 11 16 · k → ⇔ n 1 → = 11 56 , — 11 28 , 11 16 n 2 → = A B → × A D → = i → j → k → 47 8 19 16 — 1 11 4 7 8 — 1 = — 5 16 · i → + 25 8 · j → + 15 8 · k → ⇔ n 2 → = — 5 16 , 25 8 , 15 8

Приступим к нахождению скалярного произведения n 1 → = 11 56 , — 11 28 , 11 16 и n 2 → = — 5 16 , 25 8 , 15 8 .

Получим: n 1 → , n 2 → = 11 56 · — 5 16 + — 11 28 · 25 8 + 11 16 · 15 8 = 0 .

Если оно равно нулю, значит векторы плоскостей А В С и A B D перпендикулярны, тогда и сами плоскости перпендикулярны.

Ответ: плоскости перпендикулярны.

Можно было подойти к решению иначе и задействовать уравнения плоскостей А В С и A B D . После нахождения координат нормальных векторов данных плоскостей можно было бы проверить на выполнимость условие перпендикулярности нормальных векторов плоскостей.

Видео:1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Перпендикулярность плоскостей

Вы будете перенаправлены на Автор24

Видео:9. Угол между плоскостями Условия параллельности и перпендикулярности плоскостейСкачать

Понятие перпендикулярных плоскостей

При пересечении двух плоскостей у нас получается $4$ двугранных угла. Два угла равны $varphi $, а два другие равны $^0-varphi $.

Углом между плоскостями называется минимальный из двугранных углов, образованных этими плоскостями.

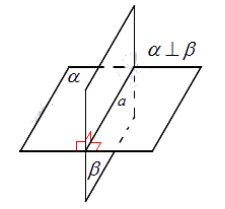
Две пересекающиеся плоскости называются перпендикулярными, если угол между этими плоскостями равен $90^circ$ (рис. 1).

Рисунок 1. Перпендикулярные плоскости

Видео:10 класс, 23 урок, Признак перпендикулярности двух плоскостейСкачать

Признак перпендикулярности двух плоскостей

Если прямая плоскости перпендикулярна другой плоскости, то эти плоскости перпендикулярны друг другу.

Доказательство.

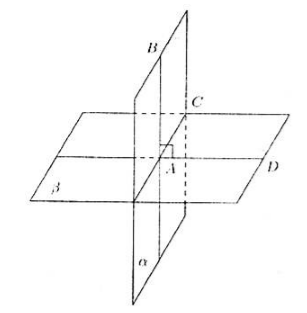
Пусть нам даны плоскости $alpha $ и $beta $, которые пересекаются по прямой $AC$. Пусть прямая $AB$, лежащая в плоскости $alpha $ перпендикулярна плоскости $beta $ (рис. 2).

Так как прямая $AB$ перпендикулярна плоскости $beta $, то она перпендикулярна и прямой $AC$. Проведем дополнительно прямую $AD$ в плоскости $beta $, перпендикулярно прямой $AC$.

Получаем, что угол $BAD$ — линейный угол двугранного угла, равный $90^circ$. То есть, по определению 1, угол между плоскостями равен $90^circ$, значит, данные плоскости перпендикулярны.

Теорема доказана.

Из этой теоремы следует следующая теорема.

Если плоскость перпендикулярна прямой, по которой пересекаются две другие плоскости, то она перпендикулярна и этим плоскостям.

Доказательство.

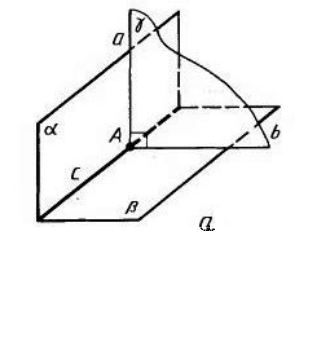
Пусть нам даны две плоскости $alpha $ и $beta $, пересекающиеся по прямой $c$. Плоскость $gamma $ перпендикулярна прямой $c$ (рис. 3)

Так как прямая $c$ принадлежит плоскости $alpha $ и плоскость $gamma $ перпендикулярна прямой $c$, то, по теореме 1, плоскости $alpha $ и $gamma $ перпендикулярны.

Так как прямая $c$ принадлежит плоскости $beta $ и плоскость $gamma $ перпендикулярна прямой $c$, то, по теореме 1, плоскости $beta $ и $gamma $ перпендикулярны.

Теорема доказана.

Для каждой из этих теорем справедливы и обратные утверждения.

Видео:Перпендикулярность плоскостей - определениеСкачать

Примеры задач

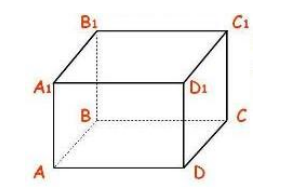
Пусть нам дан прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Найти все пары перпендикулярных плоскостей (рис. 5).

Решение.

По определению прямоугольного параллелепипеда и перпендикулярных плоскостей видим следующие восемь пар перпендикулярных между собой плоскостей: $(ABB_1)$ и $(ADD_1)$, $(ABB_1)$ и $(A_1B_1C_1)$, $(ABB_1)$ и $(BCC_1)$, $(ABB_1)$ и $(ABC)$, $(DCC_1)$ и $(ADD_1)$, $(DCC_1)$ и $(A_1B_1C_1)$, $(DCC_1)$ и $(BCC_1)$, $(DCC_1)$ и $(ABC)$.

Готовые работы на аналогичную тему

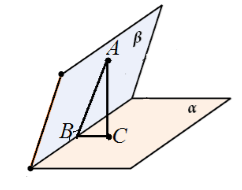
Пусть нам даны две взаимно перпендикулярные плоскости. Из точки одной плоскости проведен перпендикуляр к другой плоскости. Доказать, что эта прямая лежит в данной плоскости.

Доказательство.

Пусть нам даны перпендикулярные плоскости $alpha $ и $beta $, пересекающиеся по прямой $c$. Из точки $A$ плоскости $beta $ проведен перпендикуляр $AC$ к плоскости $alpha $. Предположим, что $AC$ не лежит в плоскости $beta $ (рис. 6).

Рассмотрим треугольник $ABC$. Он является прямоугольным с прямым углом $ACB$. Следовательно, $angle ABCne ^0$.

Но, с другой стороны, $angle ABC$ является линейным углом двугранного угла, образованного этими плоскостями. То есть двугранный угол, образованный этими плоскостями не равняется 90 градусам. Получаем, что угол между плоскостями не равен $90^circ$. Противоречие. Следовательно, $AC$ лежит в плоскости $beta $.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 27 04 2021

🔍 Видео

Теорема о трех перпендикулярах. Признак перпендикулярности плоскостей | Математика | TutorOnlineСкачать

Признак перпендикулярности плоскостейСкачать

Геометрия 10 класс (Урок№11 - Перпендикулярность плоскостей.)Скачать

Перпендикулярность прямой и плоскости. Практическая часть. 10 класс.Скачать

12. Уравнения прямой в пространстве Решение задачСкачать

3. Частные случаи общего уравнения плоскости Неполные уравнения плоскостиСкачать

Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

Двугранный угол. Признак перпендикулярности плоскостей. Видеоурок 10. Геометрия 10 классСкачать

Геометрия 10 класс (Урок№9 - Признак перпендикулярности прямой и плоскости.)Скачать

Геометрия 10 класс (Урок№8 - Перпендикулярность прямой и плоскости.)Скачать

#5str. Как проверять перпендикулярность?Скачать