Как прочитать уравнение математическим языком

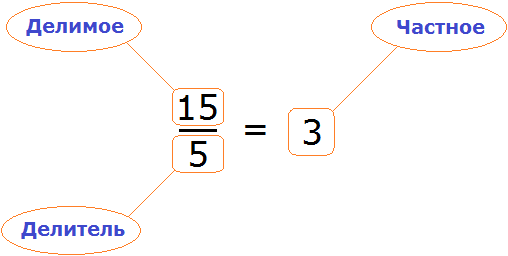
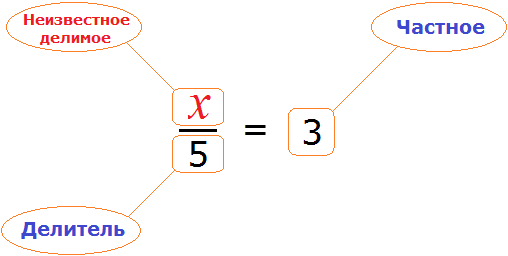
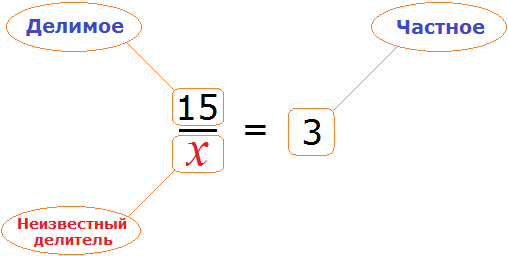
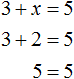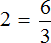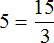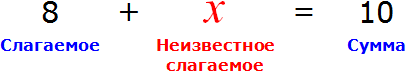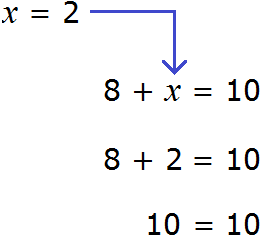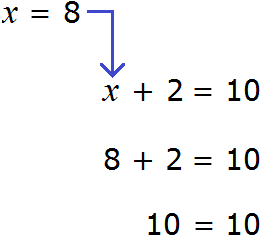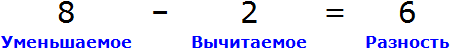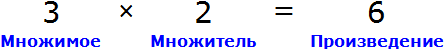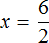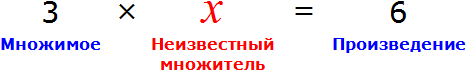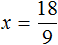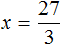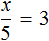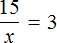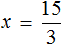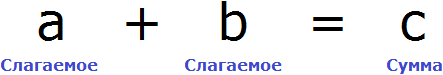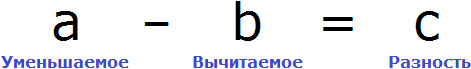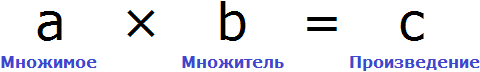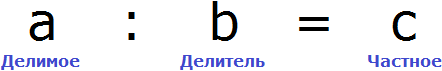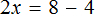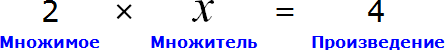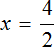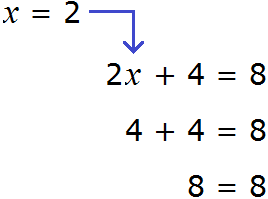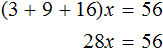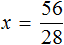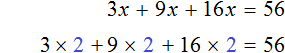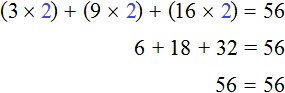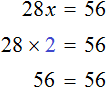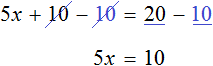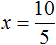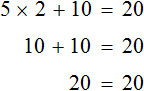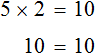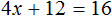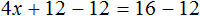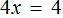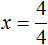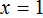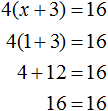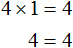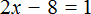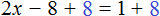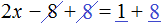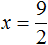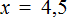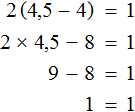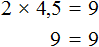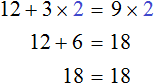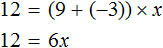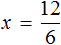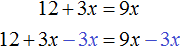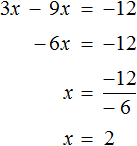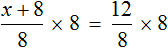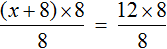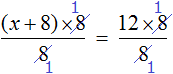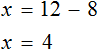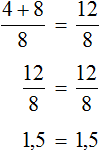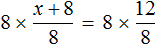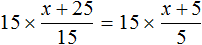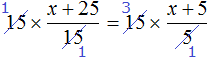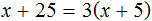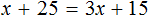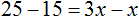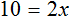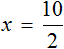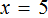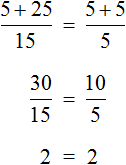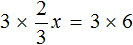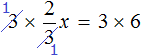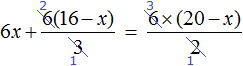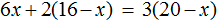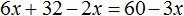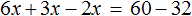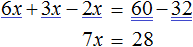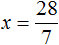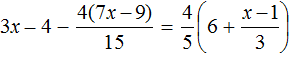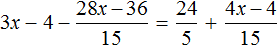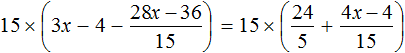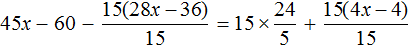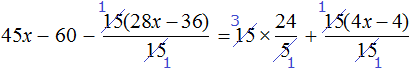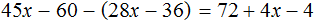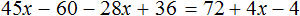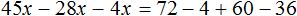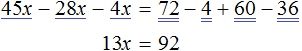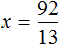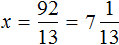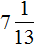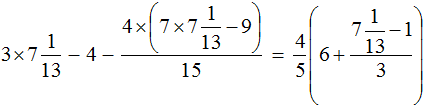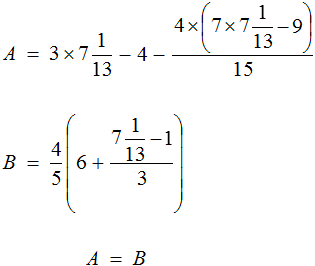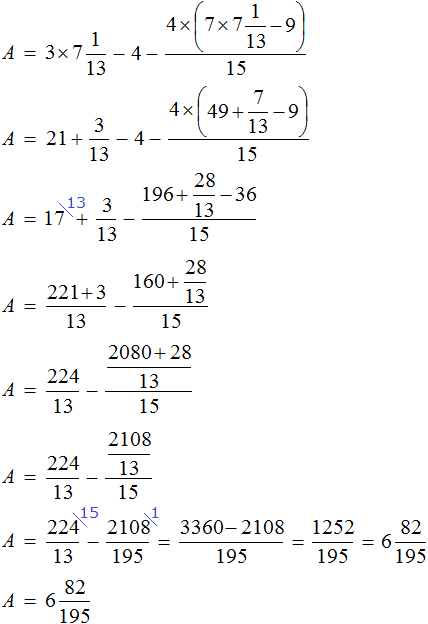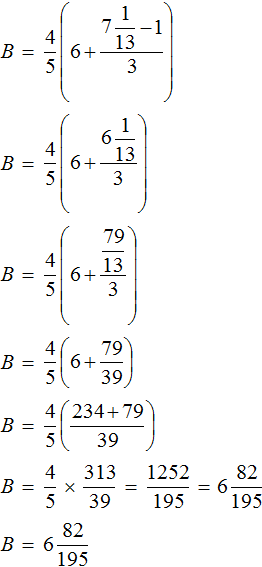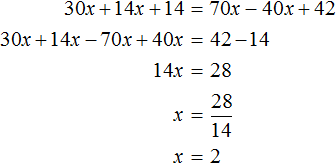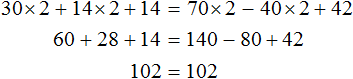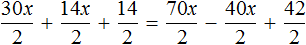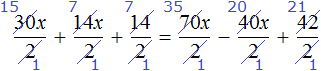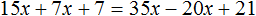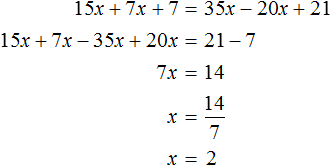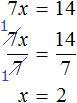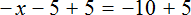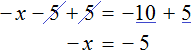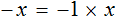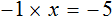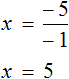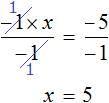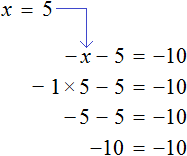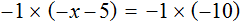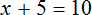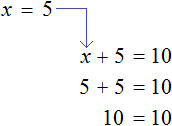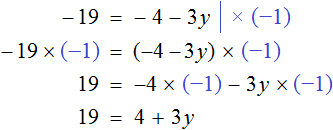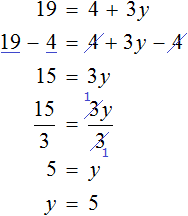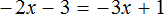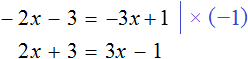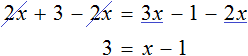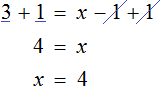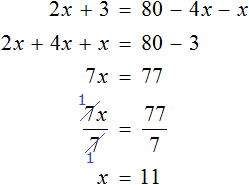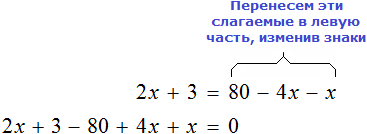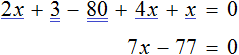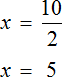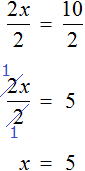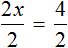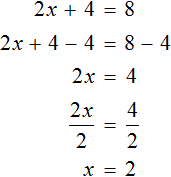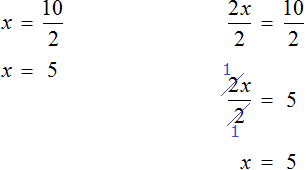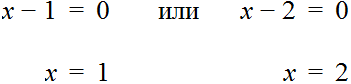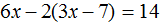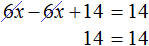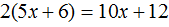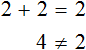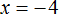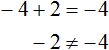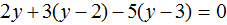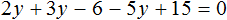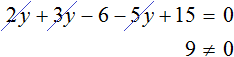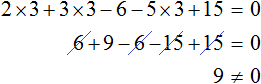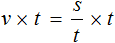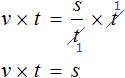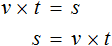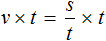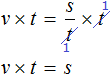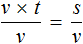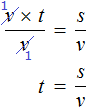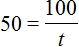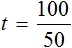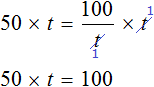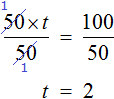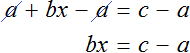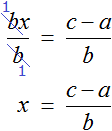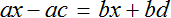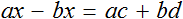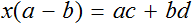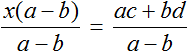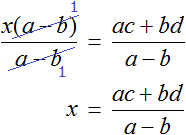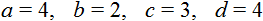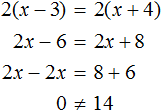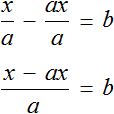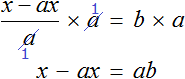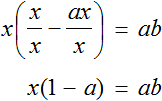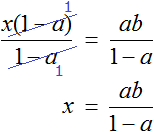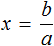Математика — это «язык, который ни читать, ни понять невозможно без инициации» (Эдвард Ротштейн, «Эмблемы ума»)

Протокол чтения — набор стратегий, которые должен использовать читатель для получения всех преимуществ от чтения текста. Набор стратегий для поэзии отличается от художественной литературы, а стратегии чтения художественной литературы отличаются от научных статей. Будет нелепо читать художественную книгу и задаваться вопросом, какие источники позволили автору утверждать, что главный герой — загорелый блондин; но будет неправильно читать научную литературу и не задать такой вопрос. Этот протокол чтения расширяется на протоколы просмотра и прослушивания в живописи и музыке. На самом деле большинство вводных курсов по литературе, музыке и искусству посвящено изучению этих протоколов.

Для математики существует особый протокол чтения. Как мы учимся читать литературу, так и математику мы должны научиться читать. Школьникам следует изучать протокол чтения для математики так же, как они учатся правилам чтения романа или стихотворения, учатся понимать музыку и живопись. Замечательная книга «Эмблемы ума» Эдварда Ротштейна выявляет взаимосвязь между математикой и музыкой, неявно затрагивая протоколы чтения для математики.

Когда мы читаем роман, нас поглощает сюжет и персонажи. Мы пытаемся следовать различным сюжетным линиям и тому, как каждая из них влияет на развитие героев. Сами персонажи должны стать для нас реальными людьми — и те, которые нас восхищают, и те, которых мы презираем. Мы не останавливаемся на каждом слове, а представляем слова как мазки на картине. Даже если конкретное слово неизвестно, общая картина всё равно ясна. Мы редко прерываемся поразмыслить над конкретной фразой или предложением. Вместо этого мы позволяем произведению увлечь нас в своём потоке и быстро донести до конца. Это полезное и расслабляющее занятие, оно даёт пищу для размышлений.

Писатели часто характеризуют персонажей, вовлекая их в тщательно подобранные эпизоды действий, а не описывая тщательно подобранными прилагательными. Они изображают один аспект, затем другой, потом снова первый в новом свете и так далее. По мере этого общая картина растёт, становится всё более ясной. Таков способ передать сложные мысли, которые не поддаются точному определению.

Математические идеи по своей сути точны и хорошо определены, так что можно дать чёткое и очень краткое описание. И математическая статья, и художественный роман рассказывают некую историю и развивают сложные идеи, но математическая статья делает это с гораздо меньшим количеством слов и символов, чем в книге. Красота книги — в эстетическом способе использования языка для пробуждения эмоций и представления вещей, которые не поддаются точному определению. Красота математической статьи — в элегантности и эффективности лаконичного выражения чётких идей огромной сложности.

Какие типичные ошибки делают люди, которые пытаются прочитать математику? Как эти ошибки можно исправить?

Видео:Проверь свои знания по математике за 11 классСкачать

Не теряй большой картины

«Чтение математики вообще не линейно… Для понимания текста нужны перекрёстные ссылки, быстрое сканирование, паузы и повторное чтение» (оттуда же)

Не думайте, что понимание каждой фразы в отдельности позволит вам понять идею целиком. Это как пытаться увидеть портрет, разглядывая в упор каждый квадратный сантиметр картины. Вы увидите детали, текстуру и цвет, но совершенно упустите портрет. Математическая статья рассказывает историю. Попробуйте понять, что это за история, прежде чем углубиться в детали. Взглянуть поближе можно позже, когда построите фреймворк понимания. Сделайте это так же, как вы могли бы перечитать художественную книгу.

Видео:Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

Не будь пассивным читателем

«Трёхстрочное доказательство скромной теоремы — это квинтэссенция лет работы. Чтение математики… предусматривает возвращение к мыслительному процессу, который происходил во время её записи» (оттуда же)

Исследуйте примеры на предмет шаблонов. Попробуйте особые случаи.

Математическая статья обычно рассказывает только малую часть большой и протяжённой истории. Как правило, автор месяцами блуждает в темноте, пытаясь открыть что-то новое. В конце концов он организует своё открытие в виде статьи, где скрывает все ошибки (и их причины) и представляет законченную идею в виде чистого аккуратного потока. Чтобы по-настоящему понять идею и воссоздать, что скрыл автор, читайте между строк.

Математики очень лаконичны, но многое скрывается за этим немногословием. Читатель должен участвовать. На каждом этапе он/она Должен решать, насколько ясна представленная идея. Задавайте себе следующие вопросы:

• Почему эта идея верна?
• Действительно ли я верю в неё?
• Могу я убедить кого-нибудь, что она верна?
• Почему автор не использовал иной аргумент?
• Есть ли у меня лучший аргумент или метод, объясняющий идею?
• Почему автор не объяснил её понятным мне способом?
• Мой способ неверен?
• Я в самом деле понял идею?
• Я упускаю какой-то нюанс?
• Автор упускает какой-то нюанс?
• Если я не могу понять смысл, может мне будет понятнее похожая, но более простая идея?
• Действительно ли так необходимо понимание этой идеи?
• Могу ли я принять эту идею без понимания деталей, почему она верна?
• Пострадает ли моё понимание большой картины от того, что я не понимаю доказательства этой конкретной идеи?

Если потратить слишком мало усилий на подобное участие, то это как читать книгу без концентрации внимания. Через полчаса вы внезапно понимаете, что просто переворачивали страницы, думая о своём, и не запомнили ничего из того, что читали.

Видео:РЕШЕНИЕ УРАВНЕНИЙ |ПОДРОБНОЕ ОБЪЯСНЕНИЕ КАК РЕШИТЬ УРАВНЕНИЯ / ПРОСТЫЕ УРАВНЕНИЯ 2 КЛАСС МАТЕМАТИКАСкачать

Не читай слишком быстро

Слишком быстрое чтение математики приводит к разочарованию. Полчаса концентрации внимания над художественной книгой позволит среднему читателю прочитать 20-60 страниц с полным пониманием текста, в зависимости от книги и опыта чтения. Те же полчаса над математической статьёй дадут 0-10 строчек, в зависимости от статьи и опыта чтения математики. Работу и время ничем нельзя заменить. Вы можете ускорить математическое чтение с помощью практики, но будьте осторожны. Как и в любом навыке, попытка сделать слишком многое слишком быстро может отбросить вас назад и уничтожить мотивацию. Представьте, что вы в течение часа энергично занимаетесь физическими упражнениями, если до этого не занимались два года. Может вы и пройдёте через первый этап, но вряд ли продолжите дальше. Разочарование от постоянного наблюдения, как опытные ребята без устали выполняют вдвое больше вашего, в то время как у вас на следующий день всё тело ноет от усталости — это слишком трудно принять.

Например, возьмём такую теорему из трактата «Дело вычислителя» Леви бен Гершома, написанного в 1321 году.

«Когда вы складываете последовательные числа, начиная с 1, и количество слагаемых нечётное, то результат равен произведению среднего числа на последнее». Для современной математики естественно будет записать теорему следующим образом:

Читателю понадобится примерно столько же времени, чтобы распутать эту небольшую формулу, сколько ему нужно на понимание двух строчек текстовой версии теоремы. Пример теоремы Леви:

Видео:Как решать уравнения с дробью? #shortsСкачать

Сделай идею свой собственной

Лучший способ понять прочитанное — сделать идею своей собственной. Это означает отследить идею к её корням и самостоятельно заново открыть её. Математики часто говорят, что для понимания чего-либо вы должны сначала прочитать это, затем записать собственными словами, а потом научить кого-то другого. У каждого разный инструментарий и разный уровень «усвоения» сложных идей. Нужно приспособить идею к собственному ви́дению и опыту.

Видео:Математика это не ИсламСкачать

«Когда я беру слово, оно означает то, что я хочу»

Видео:19 задание: Теория чисел | Математика с Кириллом Нэш | ЕГЭ 2024 | SMITUPСкачать

(Шалтай-Болтай из книги «Алиса в Зазеркалье» Льюиса Кэролла)

«Значение редко будет полностью понятным, потому что каждый символ или слово уже представляют собой экстраординарную конденсацию концепции и ссылки» (оттуда же)

Хорошо написанный математический текст будет аккуратно использовать слово только в одном смысле, делая различие, скажем, между комбинацией и перестановкой (или расстановкой). Чёткое математическое определение может подразумевать, что «жёлтая бешеная собака» и «бешеная жёлтая собака» — это разная расстановка слов, но одинаковая комбинация. Большинство англоязычных читателей не согласятся с этим. Исключительная точность совершенно чужда большей части художественной литературы и поэзии, где хорошим тоном считается использование разнообразных слов, синонимов и изменчивых описаний.

Со стороны читателя ожидается понимание, что абсолютное значение — это не какое-то произвольное значение, которое оказалось абсолютным, а функция не имеет отношения ни к чему функциональному.

Особенно печально известный пример — использование фразы «из этого легко следует, что…» и тому подобных конструкций. Они означают примерно следующее:

Теперь можно проверить справедливость следующего утверждения. Проверка потребует определённого количества по существу механической, хотя, возможно, и трудной работы. Я как автор мог бы её провести, но она займёт много места и, возможно, не приведёт к хорошим результатам, поскольку в ваших же интересах самостоятельно сделать вычисления и прояснить, что здесь происходит. Обещаю, что никакие новые идеи не участвуют. Хотя, конечно, вам может понадобиться немного подумать, чтобы найти правильную комбинацию хороших идей для применения.

Другими словами, эта фраза при правильном применении — сигнал автору, что здесь присутствует нечто утомительное и даже сложное, но не предполагающее ярких озарений. Тогда читатель волен решать, насколько сильно он хочет сам разобраться во всех подробностях или ему достаточно заверений автора — и тогда можно сказать: «Ладно, верю тебе на слово».

Теперь независимо от вашего мнения об уместности употребления подобной фразы в конкретной ситуации и от корректности использования её автором вы должны понимать, что она должна значить на самом деле. Фраза «Из этого легко следует, что…» не значит

Если ты сразу этого не видишь, ты дурак

И она не значит

Это не должно занять больше двух минут

Но человек, незнакомый с математическим словарём, может её неправильно понять и столкнётся с разочарованием. Это помимо вопроса о том, что «утомительная задача» для одного человека может оказаться сложнейшей проблемой для другого. Поэтому автор должен правильно оценивать свою аудиторию.

Видео:Считаем в уме за секунду. #математика #арифметика #счет #ментальнаяарифметика #simplemathСкачать

Знай себя

Тексты пишутся с расчётом на читателей определённого уровня. Убедитесь, что вы являетесь таким читателем или желаете сделать всё, чтобы присоединиться к их числу.

Из Томаса Элиота, «Песнь Симеона»:

Господи, зимнее солнце ползёт меж снежных вершин,
Римские гиацинты заполыхали в чашах;
Время застыло — упрямый немой властелин,
Жду дуновения смерти душой облегчённой,
Словно пушинка на старческой длани. Один.
Пыль под солнцем и память по закоулкам
Чаю прохлады, что веет для смертных долин.

Lord, the Roman hyacinths are blooming in bowls and
The winter sun creeps by the snow hills;
The stubborn season has made stand.
My life is light, waiting for the death wind,
Like a feather on the back of my hand.
Dust in sunlight and memory in corners
Wait for the wind that chills towards the dead land.

Например, стихотворение Элиота в значительной степени предполагает, что читатели или знают, кто такой Симеон, или желают выяснить это. Оно также предполагает, что читателем будет или опытный читатель поэзии, или тот, кто хочет приобрести такой опыт. Автор предполагает, что читатели либо знают, либо разберутся в аллюзиях здесь. Это выходит за рамки простых вещей вроде того, кем был Симеон. Например, почему гиацинты «римские»? Почему это важно?

Элиот предполагает, что читатель будет читать медленно и обратит внимание на картинки: автор сопоставляет пыль и память, сравнивает старость с зимой, сравнивает ожидание смерти с пушинкой на обратной стороне ладони и т.д. Он предполагает, что читатель воспримет это как поэзию; в некотором смысле, он предполагает, что читатель знаком со всей поэтической традицией. Он должен заметить, что нечётные строчки рифмуются, а остальные нет, и т.д.

Самое главное, он предполагает, что читатель будет подключать к чтению не только свой ум, но также свои эмоции и воображение, которое нарисует образ старика, уставшего от жизни но вынужденного цепляться за неё, ожидающего некоего важного события.

Большинство математических книг тоже написано с некоторыми предположениями об аудитории: что они знают определённые вещи, что они достигли определённого уровня «математической зрелости» и проч. Прежде чем начать читать, убедитесь в соответствии тому, что автор ожидает от вас.

Видео:УРАВНЕНИЕ 4 КЛАСС МАТЕМАТИКА УЧИМСЯ РЕШАТЬ УРАВНЕНИЯ МЕТОДИКА ОБУЧЕНИЯ РЕШАЕМ УРАВНЕНИЯ #уравнениеСкачать

Пример математической записи

Чтобы поэкспериментировать с представленными здесь принципами, я включил в него небольшой математический фрагмент, часто называемый парадоксом дней рождения. Первая часть — это точная математическая статья, описывающая проблему и её решение. Вторая часть — вымышленная попытка Читателя понять статью, используя соответствующий протокол чтения. Тема статьи — вероятность. Она доступна смышлёному и мотивированному читателю даже без математического образования.

Видео:Уравнение с модулемСкачать

Парадокс дней рождения

Профессор в классе из 30-ти случайных студентов часто предлагает поспорить, что как минимум у двоих человек в классе одинаковый день рождения (месяц и день, необязательно год). Вы примете спор? А если в классе меньше студентов? Примете тогда предложение поспорить?

Предположим, что дни рождения человек равномерно распределены по 365 дням года (для простоты не учитываем високосные годы). Докажем, что вероятность одинакового дня рождения (месяц и день) по крайней мере у двоих из них равна:

Какова вероятность, что среди 30-ти случайных людей в комнате попадутся хотя бы двое с одинаковым днём рождения? Для эта вероятность будет 71%, то есть профессор будет выигрывать спор в 71 случаях из 100 на длинной дистанции. Как выясняется, при 23-х учениках в классе вероятность составляет примерно 50%.

Вот доказательство: Пусть будет искомой вероятностью. Пусть будет вероятностью, что у всех разные дни рождения. Теперь найдём , вычислив количество наборов из дней рождения без дубликатов и разделив его на общее количество возможных наборов из дней рождения. Затем найдём .

Общее количество наборов из дней рождения без дубликатов:

Это потому что для первого ДР возможно 365 вариантов, для второго — 364и так далее для человек. Общее количество дней рождения без всяких ограничений равняется просто , потому что для каждого из дней рождения есть 365 вариантов. Таким образом, равняется

Решение для даёт и, следовательно, наш результат.

Видео:Математика 2 класс (Урок№26 - Уравнение. Решение уравнений подбором неизвестного числа.)Скачать

Попытки нашего читателя понять парадокс дней рождения

В этом разделе наивный Читатель пытается понять смысл последних нескольких абзацев. Реплики Читателя — метафорическое выражение его мыслей вслух, а комментарии Профессионала представляют собой исследовательскую работу, которую должен проделать Читатель. Соответствующие протоколы выделены жирным шрифтом и вставлены в соответствующие места повествования.

Выглядит, что Читатель как будто схватывает вещи очень быстро. Но будьте уверены, что в реальности между комментариями Читателя проходит немало времени и что я оставил за скобками многие его замечания, которые ведут в тупик. Понять, что он испытывает, можно только если читать между строк и представить образ его мыслей. Думать за него — часть ваших собственных усилий.

Знай себя

Читатель (Ч): Я ничего не знаю о вероятностях, я смогу в этом разобраться?

Профессионал (П): Давай попробуем. Возможно, придётся делать большие отступления на каждом шаге.

Ч: Что означает фраза «30 случайных (хаотичных) студентов»?

«Когда я беру слово, оно означает то, что я хочу, ни больше и ни
меньше»

П: Хороший вопрос. Фраза не означает, что у нас 30 ошалевших или больных на голову людей. Она означает, что мы должны предположить, что дни рождения этих 30-ти человек не зависят друг от друга и что каждый день рождения одинаково вероятен для каждого человека. Чуть далее автор более формально описывает это: «Предположим, что дни рождения человек равномерно распределены по 365 дням года».

Ч: Разве это не очевидно? Зачем специально это оговаривать?

П: Да, предположение кажется очевидным. Автор просто устанавливает основное условие. Это предложение гарантирует, что всё нормально, а решение не предполагает какой-либо воображаемой причудливой научной фантастики.

Ч: Что ты имеешь в виду?

П: Например, автор не ищет решения вроде такого: все живут в Стране Независимости и родились 4-го июля, так что шансы на совпадение дней рождения двух и более людей составляют 100%. Математикам не нравятся решения такого рода. Кстати, предположение также подразумевает, что мы не учитываем високосные годы. То есть никто в этой задаче не родился 29-го февраля. Читай дальше.

Ч: Не понимаю эту длинную формулу, Что такое ?

П: Автор решает проблему для произвольного количества человек, не просто для 30-ти. С этого момента автор называет количество человек .

Ч: Я по-прежнему не понимаю. Какой ответ?

Не будь пассивным читателем – попробуй примеры

П: Ну если нужен ответ только для 30-ти, просто установи .

Ч: Окей, но это сложно посчитать. Где мой калькулятор? Посмотрим: 365×364×363×. ×336. Это утомительно, и результат даже не помещается на экране. Здесь написано:

Если даже зная формулу я не могу вычислить результат, как я могу понять, откуда взялась формула?

П: Ты прав, что здесь получается не точный результат, но если продолжить дальше и поделить, то ответ будет не слишком далёк от точного.

Ч: Всё это как-то некомфортно. Я бы хотел вычислить точное значение. Есть другой способ произвести вычисления?

П: Сколько множителей у тебя в числителе? Сколько в знаменателе?

Ч: Ты имеешь в виду 365 как первый множитель, 364 как второй? Тогда получается 30 множителей вверху. Также 30 множителей внизу (30 копий 365).

П: Теперь можешь вычислить результат?

Ч: А, понятно. Я могу спарить каждый множитель из числителя с каждым множителем знаменателя, так что получится 365/365 для первого множителя, затем умножить на 364/365 и так далее для всех 30-ти множителей. Так что результат всегда поместится в моём калькуляторе. (Через несколько минут)… Так, я получил 0,29368, если округлить до пяти знаков.

П: Что значит это число?

Не теряй большой картины

Ч: Я забыл, что делал. Так, посмотрим. Я искал ответ для . Число 0,29368 — это все вычисления, кроме вычитания из единицы. Если продолжить, получится 0,70632. А теперь что это значит?

П: Тут полезно больше узнать о вероятностях, но по-простому это означает, что в группе из 30-ти человек у двух или более совпадут дни рождения в 70 632 из 100 000 случаев, то есть примерно в 71% случаев.

Ч: Интересно. Я бы сам не догадался. Хочешь сказать, что в моём классе из 30-ти студентов довольно высока вероятность, что по крайней мере у двух человек будет одинаковый день рождения?

П: Да, правильно. Можешь принимать ставки до того, как узнал их даты рождения. Многие думают, что такое совпадение маловероятно. Вот почему некоторые авторы называют это парадоксом дней рождения.

Ч: Так вот почему я должен читать математику, чтобы заработать пару долларов?

П: Понимаю, что для тебя это может быть неким стимулом, но надеюсь, что математика также вдохновляет тебя и без всяких денежных перспектив.

Ч: Интересно, какой результат будет для других значений . Попробую сделать ещё несколько вычислений.

П: Хорошая мысль. Мы даже можем составить графическое изображение из всех твоих вычислений. Можно составить график количества людей и вероятностей совпадения дней рождения, хотя это можно оставить на другой раз.

Ч: О, смотри, автор сделал некоторые вычисления за меня. Он говорит, что для ответ около 71%; я тоже получил такую цифру. А для получается около 50%. Это имеет смысл? Думаю, что имеет. Чем больше людей, тем выше вероятность совпадения дней рождения. Эй, я опережаю автора. Неплохо. Ладно, продолжим.

П: Хорошо, теперь сам скажешь, когда продолжить.

Не читай слишком быстро

Ч: Кажется, что мы добрались до доказательства. Оно должно объяснить, почему формула работает. Что это за ? Думаю, что означает “probability ” (вероятность), но что означает ?

П: Автор вводит новую величину. Он использует просто потому что это следующая буква в алфавите после , но — это тоже вероятность, причём имеющая близкое отношение к . Пришло время взять минутку на раздумье. Что такое и почему оно равняется ?

Ч: — это вероятность, что ни у кого в комнате не совпадают дни рождения. Почему автора волнует этот вопрос? Разве нам не нужна другая вероятность, что дни рождения совпадают?

П: Хорошее замечание. Автор не говорит этого явно, но между строк ты можешь понять, что он понятия не имеет, как напрямую вычислить . Вместо этого он вводит вероятность , которая предположительно равна . Вероятно, после этого автор должен показать, как вычисляется . Кстати, когда ты закончишь статью, ты можешь задаться вопросом, как вычислить напрямую. Это прекрасное продолжение для идей, представленных здесь.

Ч: Всему своё время.

П: Ладно. Итак, теперь мы знаем , что дальше?

Ч: Затем мы можем получить . Если , то . Хорошо, но почему ? Автор полагает, что это очевидно?

П: Да, он так полагает, и что ещё хуже, он даже не говорит нам, что это очевидно. Вот эмпирическое правило: когда автор явно говорит, что это истина или это очевидно, то следует потратить 15 минут и убедить себя, что так оно и есть. Если автор даже не беспокоиться о том, чтобы это сказать, но подразумевает это, то процесс займёт немного больше времени.

Ч: Как я пойму, что нужно остановиться и подумать?

П: Просто будь честен с собой. Если появились сомнения, остановись и подумай. Если слишком устал, иди посмотри телевизор.

Ч: Так почему ?

П: Давай вообразим особый случай. Если вероятность совпадения двух и более дней рождения 1/3, то какова вероятность не получить совпадение?

Ч: Это 2/3, потому что вероятность отсутствия события обратна вероятности наступления события.

Сделай идею свой собственной

П: Ну, следует быть осторожным при использовании слов вроде обратна, но ты прав. На самом деле ты открыл одно из первых правил, которое изучают в теории вероятностей. А именно, что вероятность отсутствия события равна единице минус вероятность наступления события. Теперь перейдём к следующему абзацу.

Ч: Там вроде объясняется, чему равняется — в длинной и сложной на вид формуле. Я никогда такую не пойму.

П: Формула для тяжела для понимания, и автор рассчитывает на твоё усердие, упорство и/или имеющиеся знания, чтобы разобраться в ней.

Ч: Он как будто вычисляет все вероятности чего-то и делит их на общее количество вероятностей, что бы это ни значило. Понятия не имею, почему он так делает.

П: Может быть, могу помочь тебе с некоторой информацией по этому предмету. Вероятность наступления определённого исхода в математике определяется так: общее количество возможных вариантов этого исхода делится на общее количество всех вариантов исхода. Например, вероятность выбросить четвёртку на кубике равна 1/6. Поскольку там одна четвёрка и шесть возможных исходов. Какова будет вероятность, что ты выбросишь четвёрку или тройку?

Ч: Ну, я думаю, 2/6 (или 1/3), потому что общее количество возможных исходов по-прежнему осталось шесть, но у меня есть два варианта удачного исхода.

П: Хорошо. Теперь более сложный пример. Что насчёт вероятности выбросить четыре в сумме при бросании двух кубиков? Есть три варианта получить такую сумму (1-3, 2-2, 3-1), в то время как общее количество комбинаций равно 36. Это 3/36 или 1/12. Посмотри на следующую таблицу 6×6 и сам убедись в этом.

Что насчёт вероятности выбросить семь в сумме?

Ч: Погоди, что значит 1-1? Разве это не равняется 0?

П: Извини, я виноват. Я использовал знак минуса как тире, просто имея в виду пару чисел, так что 1-1 означает выбросить единички на обоих кубиках.

Ч: Ты не мог бы придумать лучшую запись?

П: Ну может я могу или должен сделать это, но запятые выглядят хуже, а слэш будет похож на деление, и всё остальное тоже может вводить в заблуждение. В любом случае, мы не собираемся публиковать эту расшифровку.

Ч: Слава богу. Ну, теперь-то я знаю, что ты имеешь в виду. Я могу получить семь в сумме шестью способами: 1-6, 2-5, 3-4, 4-3, 5-2 или 6-1. Общее количество исходов по-прежнему 36, так что получается 6/36 или 1/6. Это странно, почему вероятность выпадения четырёх отличается от вероятности выпадения семи?

П: Потому что не каждая сумма одинаково вероятна. Здесь ситуация отличается от простого вращения колеса с цифрами от 2 до 12 в одинаковых интервалах. В этом случае у каждой из 11 цифр одинаковая вероятность выпадения 1/11.

Ч: Хорошо, теперь я эксперт. Вероятность вычисляется просто подсчётом?

П: Иногда да. Хотя рассчитать бывает непросто.

Ч: Ясно, давай продолжим. Кстати, автор реально ожидал, что я всё это знаю? Мой друг проходит курс вероятности и статистики, но я не уверен, что он знает все эти вещи.

П: Маленький раздел математики содержит в себе много информации. Да, автор ожидает от читателя знания всего этого или что тот найдёт эту информацию и усвоит её, как это сделали мы. Если бы меня здесь не было, тебе пришлось бы задавать эти вопросы самому себе и находить ответы путём размышлений, в учебниках и справочниках или консультируясь с другом.

Ч: Так что вероятность совпадения дней рождения у двух человек — это количество возможных наборов из дней рождения без дубликатов, поделенное на общее количество возможных наборов из дней рождения.

П: Отличное резюме.

Ч: Мне не нравится использование , так что давай использовать 30. Возможно, тогда будет проще усвоить обобщение .

П: Отличная мысль. Часто бывает полезным проанализировать особый случай, чтобы понять общий случай.

Ч: Так сколько наборов из 30-ти дней рождения есть вообще? Я не могу посчитать. Думаю, что мне придётся ещё больше ограничить условия. Давай притворимся, что у нас всего два человека.

П: Хорошо. Теперь ты размышляешь как математик. Рассмотрим . Сколько здесь возможных комбинаций дней рождения?

Ч: Я считаю дни рождения с 1 по 365, не учитывая високосные годы. Тогда вот все возможные комбинации:

П: Когда ты пишешь 1-1, ты имеешь в виду 1-1=0, как вычитание?

Ч: Хватит меня дразнить. Ты точно знаешь, что я имею в виду.

П: Да, я знаю, и могу отметить хороший выбор способа записи. Теперь сколько здесь пар дней рождения?

Ч: Для двух человек получается 365×365 вариантов.

П: А сколько вариантов, если не учитывать совпадающие дни рождения?

Ч: Нельзя использовать 1-1, 2-2, 3-3… 365-365, так что выходит

Общее количество вариантов выходит 365×364, потому что в каждой строке теперь 364 пары вместо 365.

П: Хорошо. Ты здесь немного спешишь, но всё равно на 100% прав. Теперь можешь обобщить для 30-ти человек? Каково общее количество возможных наборов из 30-ти дней рождения? Попробуй догадаться. У тебя это хорошо получается.

Ч: Ну если пробовать догадаться (хотя это в реальности не совсем догадка, в конце концов, я уже знаю формулу), то я бы сказал, что для 30-ти человек нужно 30 раз умножить 365×365×. ×365, для общего количества возможных наборов ДР.

П: Точно. Математики пишут 365 30 . А каково общее количество наборов из 30-ти дней рождения без повторений?

Ч: Я знаю, что ответ должен быть 365×364×363×362×. ×336 (то есть начать с 365 и каждый раз умножать на число с вычитанием единицы 30 раз), но я не уверен, что действительно понимаю, почему именно так. Возможно, сначала нужно рассмотреть случай с тремя людьми и найти способ увеличения до 30-ти?

П: Блестящая мысль. Давай закончим на сегодня. Общая картина для тебя понятна. Когда отдохнёшь и у тебя будет больше времени, можешь вернуться и заполнить последний пробел в понимании.

Ч: Большое спасибо; это был хороший опыт. Увидимся позже.

Видео:Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Числовые и буквенные выражения. Формулы

Так же, как и у нашего языка общения есть алфавит и знаки-помощники (точка, тире, запятая и т.д.), математический язык вычисления также имеет свой алфавит:

• цифры (0, 1, 2, 3, 4, 5, 6, 7, 8, 9);
• буквы латинского и греческого алфавитов ((a, b, c, d, α, β, γ, δ) и т.д.)
• знаки математических действий ( (+, -, times , div), и т.д.);
• скобки (), [], <>.

Буквы и цифры в математике служат для обозначения чисел.

Цифрами обозначается конкретное, какое-то определённое число.

Буквами – любое или неизвестное число, в зависимости от задачи.

• 258 – конкретное числодвести пятьдесят восемь;
• (a + b) – сумма любых двух чисел;
• (x + 24 = 78) – уравнение с неизвестным первым слагаемым икс.

МАТЕМАТИЧЕСКИЕ ВЫРАЖЕНИЯ – это «слова» и «фразы» математики, записи, в которых содержатся:

• числа, обозначенные цифрами или буквами,
• знаки математических действий, которые связывают эти числа математическими действиями;
• вспомогательные знаки – скобки.

При этом знаки математических действий и вспомогательные знаки ОБЯЗАТЕЛЬНО связывают числа и обозначают последовательность действий над ними.

Примеры математических выражений:

ВНИМАНИЕ!

НЕ ЯВЛЯЕТСЯ математическим выражением:

• запись только знака;
• запись, не обозначающая математического действия над числами (когда знаки не связывают собой числа и не указывают на последовательность действий);
• запись, в которой присутствуют знаки сравнения (в этом случае запись является уравнением или неравенством, сравнивающем два и более выражений).

Например, это НЕ математические выражения:

• (
• +
• ((div 8-59)
• (35cdot 12(+74)
• (a+5=12)
• (38+87

Видео:РЕШЕНИЕ УРАВНЕНИЙ ЛЕГКО ! 1 КЛАСС МАТЕМАТИКА УРАВНЕНИЯ - ПЕТЕРСОН / ОБЪЯСНЕНИЕ КАК РЕШАТЬ УРАВНЕНИЯСкачать

Случаи опускания знака умножения в выражениях

В буквенных выражениях обычно знак умножения пишут только между числами, которые выражены цифрами.

В остальных случаях знак умножения опускают, например:

• между числовым и буквенным множителем: (5cdot x = 5x)
• между буквенными множителями: (acdot b = ab)
• между числовым множителем и скобкой: (3cdot (d+c)=3(d+c))
• между буквенным множителем и скобкой: (acdot (b+c)=a(b+c))

Видео:Быстрый способ решения квадратного уравненияСкачать

Как читать математические выражения

Простейшие математические выражения, состоящие из одного математического действия, называются по названию результата этого действия:

• (2+3) – суммачисел 2 и 3
• (5cdot 4) – произведение чисел 5 и 4
• (24div 6) – частноечисел 24 и 6
• (35-5) – разность чисел 35 и 5

Более сложные выражения, называют по последнему выполняемому действию:

• ((a+b)-c) – разность суммы чисел a и b и числа c
• ((a+b)cdot (a-b)) – произведение суммы чисел a и b и разности чисел a и b
• (adiv (ccdot d)) – частное числа a и произведения чисел c и d

Важно не только уметь читать готовые математические выражения, но и «переводить» слова на математический язык – язык чисел, знаков действия и других символов:

• Сумма первых пяти натуральных чисел – (1+2+3+4+5)
• Произведение всех однозначных чисел – (1cdot 2cdot 3cdot 4cdot 5cdot 6cdot 7cdot 8cdot 9)
• Сумма всех двузначных чётных чисел – (10+12+14+…+94+96+98)

Алгоритм чтения математических выражений

Чтобы прочитать математическое выражение, нужно:

1. Определить порядок действий в выражении
2. Прочитать, начиная с последнего действия

При чтении сложного выражения повторяем действия алгоритма столько раз, сколько необходимо.

• (35cdot (28-12)) – Произведение числа 35 и разности чисел 28 и 12
• (35cdot (28-12)+64) – Сумма произведения числа 35 с разностью чисел 28 и 12, и числа 64.
• (35cdot (28-12)+64–32div 16) – Разность суммы произведения числа 35 и разности чисел 28 и 12 с числом 64, и частного чисел 32 и 16

Видео:САМЫЙ легкий способ УМНОЖЕНИЯ 😊Лайфхак, будет полезен, тем кто не может запомнить таблицу умноженияСкачать

Формулы

Используя математические выражения можно одну величину представить в виде другой, то есть, установить зависимость значения одной величины от значения другой величины.

Велосипедист едет со скоростью (v_) км/ч. Найти скорость:

а) автомобиля, если известно, что он едет в 3 раза быстрее: (v_=3cdot v_);

б) пешехода, если известно, что он двигается на 15 км/ч медленнее: (v_

= v_-15).

Иначе это называется выразить одну величину через другую.

Многие величины в математике имеют свои собственные обозначения. Например: S – площадь фигуры, P – периметр, t – время и т.д.

Запись такого равенства называется формулой.

ФОРМУЛА – это запись зависимости значения некоторой величины от значений одной или нескольких других величин. Или другими словами, это запись правила вычисления одной неизвестной величины при помощи известных других.

• формула расстояния (s = vcdot t) (или (s = vt) ) – это запись зависимости значения пройденного расстояния от значений скорости движения и времени движения (Расстояние – это скорость, умноженная на время).
• формула периметра прямоугольника (P=2(a+b)) – это запись зависимости величины периметра
  прямоугольника от его длины и ширины (Периметр прямоугольника равен удвоенной сумме
  двух его разных сторон).

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 3.3 / 5. Количество оценок: 8

Видео:4 класс: как легко составить уравнение по задаче?Скачать

Общие сведения об уравнениях

Уравнения — одна из сложных тем для усвоения, но при этом они являются достаточно мощным инструментом для решения большинства задач.

С помощью уравнений описываются различные процессы, протекающие в природе. Уравнения широко применяются в других науках: в экономике, физике, биологии и химии.

В данном уроке мы попробуем понять суть простейших уравнений, научимся выражать неизвестные и решим несколько уравнений. По мере усвоения новых материалов, уравнения будут усложняться, поэтому понять основы очень важно.

Видео:Удалили с экзамена ОГЭ Устное Собеседование shorts #shortsСкачать

Что такое уравнение?

Уравнение — это равенство, содержащее в себе переменную, значение которой требуется найти. Это значение должно быть таким, чтобы при его подстановке в исходное уравнение получалось верное числовое равенство.

Например выражение 3 + 2 = 5 является равенством. При вычислении левой части получается верное числовое равенство 5 = 5 .

А вот равенство 3 + x = 5 является уравнением, поскольку содержит в себе переменную x , значение которой можно найти. Значение должно быть таким, чтобы при подстановке этого значения в исходное уравнение, получилось верное числовое равенство.

Другими словами, мы должны найти такое значение, при котором знак равенства оправдал бы свое местоположение — левая часть должна быть равна правой части.

Уравнение 3 + x = 5 является элементарным. Значение переменной x равно числу 2. При любом другом значении равенство соблюдáться не будет

Говорят, что число 2 является корнем или решением уравнения 3 + x = 5

Корень или решение уравнения — это значение переменной, при котором уравнение обращается в верное числовое равенство.

Корней может быть несколько или не быть совсем. Решить уравнение означает найти его корни или доказать, что корней нет.

Переменную, входящую в уравнение, иначе называют неизвестным. Вы вправе называть как вам удобнее. Это синонимы.

Примечание. Словосочетание «решить уравнение» говорит самó за себя. Решить уравнение означает «уравнять» равенство — сделать его сбалансированным, чтобы левая часть равнялась правой части.

Видео:Как решать квадратные уравнения без дискриминантаСкачать

Выразить одно через другое

Изучение уравнений по традиции начинается с того, чтобы научиться выражать одно число, входящее в равенство, через ряд других. Давайте не будем нарушать эту традицию и поступим также.

Рассмотрим следующее выражение:

Данное выражение является суммой чисел 8 и 2. Значение данного выражения равно 10

Получили равенство. Теперь можно выразить любое число из этого равенства через другие числа, входящие в это же равенство. К примеру, выразим число 2.

Чтобы выразить число 2, нужно задать вопрос: «что нужно сделать с числами 10 и 8, чтобы получить число 2». Понятно, что для получения числа 2, нужно из числа 10 вычесть число 8.

Так и делаем. Записываем число 2 и через знак равенства говорим, что для получения этого числа 2 мы из числа 10 вычли число 8:

Мы выразили число 2 из равенства 8 + 2 = 10 . Как видно из примера, ничего сложного в этом нет.

При решении уравнений, в частности при выражении одного числа через другие, знак равенства удобно заменять на слово «есть». Делать это нужно мысленно, а не в самом выражении.

Так, выражая число 2 из равенства 8 + 2 = 10 мы получили равенство 2 = 10 − 8 . Данное равенство можно прочесть так:

2 есть 10 − 8

То есть знак = заменен на слово «есть». Более того, равенство 2 = 10 − 8 можно перевести с математического языка на полноценный человеческий язык. Тогда его можно будет прочитать следующим образом:

Число 2 есть разность числа 10 и числа 8

Число 2 есть разница между числом 10 и числом 8.

Но мы ограничимся лишь заменой знака равенства на слово «есть», и то будем делать это не всегда. Элементарные выражения можно понимать и без перевода математического языка на язык человеческий.

Вернём получившееся равенство 2 = 10 − 8 в первоначальное состояние:

Выразим в этот раз число 8. Что нужно сделать с остальными числами, чтобы получить число 8? Верно, нужно из числа 10 вычесть число 2

Вернем получившееся равенство 8 = 10 − 2 в первоначальное состояние:

В этот раз выразим число 10. Но оказывается, что десятку выражать не нужно, поскольку она уже выражена. Достаточно поменять местами левую и правую часть, тогда получится то, что нам нужно:

Пример 2. Рассмотрим равенство 8 − 2 = 6

Выразим из этого равенства число 8. Чтобы выразить число 8 остальные два числа нужно сложить:

Вернем получившееся равенство 8 = 6 + 2 в первоначальное состояние:

Выразим из этого равенства число 2. Чтобы выразить число 2, нужно из 8 вычесть 6

Пример 3. Рассмотрим равенство 3 × 2 = 6

Выразим число 3. Чтобы выразить число 3, нужно 6 разделить 2

Вернем получившееся равенство 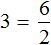в первоначальное состояние:

Выразим из этого равенства число 2. Чтобы выразить число 2, нужно 6 разделить 3

Пример 4. Рассмотрим равенство

Выразим из этого равенства число 15. Чтобы выразить число 15, нужно перемножить числа 3 и 5

Вернем получившееся равенство 15 = 3 × 5 в первоначальное состояние:

Выразим из этого равенства число 5. Чтобы выразить число 5, нужно 15 разделить 3

Видео:Математика 3 класс (Урок№2 - Решение уравнений способом подбора неизвестного. Буквенные выражения.)Скачать

Правила нахождения неизвестных

Рассмотрим несколько правил нахождения неизвестных. Возможно, они вам знакомы, но не мешает повторить их ещё раз. В дальнейшем их можно будет забыть, поскольку мы научимся решать уравнения, не применяя эти правила.

Вернемся к первому примеру, который мы рассматривали в предыдущей теме, где в равенстве 8 + 2 = 10 требовалось выразить число 2.

В равенстве 8 + 2 = 10 числа 8 и 2 являются слагаемыми, а число 10 — суммой.

Чтобы выразить число 2, мы поступили следующим образом:

То есть из суммы 10 вычли слагаемое 8.

Теперь представим, что в равенстве 8 + 2 = 10 вместо числа 2 располагается переменная x

В этом случае равенство 8 + 2 = 10 превращается в уравнение 8 + x = 10 , а переменная x берет на себя роль так называемого неизвестного слагаемого

Наша задача найти это неизвестное слагаемое, то есть решить уравнение 8 + x = 10 . Для нахождения неизвестного слагаемого предусмотрено следующее правило:

Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.

Что мы в принципе и сделали, когда выражали двойку в равенстве 8 + 2 = 10 . Чтобы выразить слагаемое 2, мы из суммы 10 вычли другое слагаемое 8

А сейчас, чтобы найти неизвестное слагаемое x , мы должны из суммы 10 вычесть известное слагаемое 8:

Если вычислить правую часть получившегося равенства, то можно узнать чему равна переменная x

Мы решили уравнение. Значение переменной x равно 2 . Для проверки значение переменной x отправляют в исходное уравнение 8 + x = 10 и подставляют вместо x. Так желательно поступать с любым решённым уравнением, поскольку нельзя быть точно уверенным, что уравнение решено правильно:

В результате получается верное числовое равенство. Значит уравнение решено правильно.

Это же правило действовало бы в случае, если неизвестным слагаемым было бы первое число 8.

В этом уравнении x — это неизвестное слагаемое, 2 — известное слагаемое, 10 — сумма. Чтобы найти неизвестное слагаемое x , нужно из суммы 10 вычесть известное слагаемое 2

Вернемся ко второму примеру из предыдущей темы, где в равенстве 8 − 2 = 6 требовалось выразить число 8.

В равенстве 8 − 2 = 6 число 8 это уменьшаемое, число 2 — вычитаемое, число 6 — разность

Чтобы выразить число 8, мы поступили следующим образом:

То есть сложили разность 6 и вычитаемое 2.

Теперь представим, что в равенстве 8 − 2 = 6 вместо числа 8 располагается переменная x

В этом случае переменная x берет на себя роль так называемого неизвестного уменьшаемого

Для нахождения неизвестного уменьшаемого предусмотрено следующее правило:

Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое.

Что мы и сделали, когда выражали число 8 в равенстве 8 − 2 = 6 . Чтобы выразить уменьшаемое 8, мы к разности 6 прибавили вычитаемое 2.

А сейчас, чтобы найти неизвестное уменьшаемое x , мы должны к разности 6 прибавить вычитаемое 2

Если вычислить правую часть, то можно узнать чему равна переменная x

Теперь представим, что в равенстве 8 − 2 = 6 вместо числа 2 располагается переменная x

В этом случае переменная x берет на себя роль неизвестного вычитаемого

Для нахождения неизвестного вычитаемого предусмотрено следующее правило:

Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.

Что мы и сделали, когда выражали число 2 в равенстве 8 − 2 = 6. Чтобы выразить число 2, мы из уменьшаемого 8 вычли разность 6.

А сейчас, чтобы найти неизвестное вычитаемое x, нужно опять же из уменьшаемого 8 вычесть разность 6

Вычисляем правую часть и находим значение x

Вернемся к третьему примеру из предыдущей темы, где в равенстве 3 × 2 = 6 мы пробовали выразить число 3.

В равенстве 3 × 2 = 6 число 3 — это множимое, число 2 — множитель, число 6 — произведение

Чтобы выразить число 3 мы поступили следующим образом:

То есть разделили произведение 6 на множитель 2.

Теперь представим, что в равенстве 3 × 2 = 6 вместо числа 3 располагается переменная x

В этом случае переменная x берет на себя роль неизвестного множимого.

Для нахождения неизвестного множимого предусмотрено следующее правило:

Чтобы найти неизвестное множимое, нужно произведение разделить на множитель.

Что мы и сделали, когда выражали число 3 из равенства 3 × 2 = 6 . Произведение 6 мы разделили на множитель 2.

А сейчас для нахождения неизвестного множимого x , нужно произведение 6 разделить на множитель 2.

Вычисление правой части позволяет нам найти значение переменной x

Это же правило применимо в случае, если переменная x располагается вместо множителя, а не множимого. Представим, что в равенстве 3 × 2 = 6 вместо числа 2 располагается переменная x .

В этом случае переменная x берет на себя роль неизвестного множителя. Для нахождения неизвестного множителя предусмотрено такое же, что и для нахождения неизвестного множимого, а именно деление произведения на известный множитель:

Чтобы найти неизвестный множитель, нужно произведение разделить на множимое.

Что мы и сделали, когда выражали число 2 из равенства 3 × 2 = 6 . Тогда для получения числа 2 мы разделили произведение 6 на множимое 3.

А сейчас для нахождения неизвестного множителя x мы разделили произведение 6 на множимое 3.

Вычисление правой части равенства 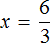позволяет узнать чему равно x

Множимое и множитель вместе называют сомножителями. Поскольку правила нахождения множимого и множителя совпадают, мы можем сформулировать общее правило нахождения неизвестного сомножителя:

Чтобы найти неизвестный сомножитель, нужно произведение разделить на известный сомножитель.

Например, решим уравнение 9 × x = 18 . Переменная x является неизвестным сомножителем. Чтобы найти этот неизвестный сомножитель, нужно произведение 18 разделить на известный сомножитель 9

Отсюда .

Решим уравнение x × 3 = 27 . Переменная x является неизвестным сомножителем. Чтобы найти этот неизвестный сомножитель, нужно произведение 27 разделить на известный сомножитель 3

Отсюда .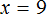

Вернемся к четвертому примеру из предыдущей темы, где в равенстве требовалось выразить число 15. В этом равенстве число 15 — это делимое, число 5 — делитель, число 3 — частное.

Чтобы выразить число 15 мы поступили следующим образом:

То есть умножили частное 3 на делитель 5.

Теперь представим, что в равенстве вместо числа 15 располагается переменная x

В этом случае переменная x берет на себя роль неизвестного делимого.

Для нахождения неизвестного делимого предусмотрено следующее правило:

Чтобы найти неизвестное делимое, нужно частное умножить на делитель.

Что мы и сделали, когда выражали число 15 из равенства . Чтобы выразить число 15, мы умножили частное 3 на делитель 5.

А сейчас, чтобы найти неизвестное делимое x , нужно частное 3 умножить на делитель 5

Вычислим правую часть получившегося равенства. Так мы узнаем чему равна переменная x .

Теперь представим, что в равенстве вместо числа 5 располагается переменная x .

В этом случае переменная x берет на себя роль неизвестного делителя.

Для нахождения неизвестного делителя предусмотрено следующее правило:

Чтобы найти неизвестный делитель, нужно делимое разделить на частное.

Что мы и сделали, когда выражали число 5 из равенства . Чтобы выразить число 5, мы разделили делимое 15 на частное 3.

А сейчас, чтобы найти неизвестный делитель x , нужно делимое 15 разделить на частное 3

Вычислим правую часть получившегося равенства. Так мы узнаем чему равна переменная x .

Итак, для нахождения неизвестных мы изучили следующие правила:

• Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое;
• Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое;
• Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность;
• Чтобы найти неизвестное множимое, нужно произведение разделить на множитель;
• Чтобы найти неизвестный множитель, нужно произведение разделить на множимое;
• Чтобы найти неизвестное делимое, нужно частное умножить на делитель;
• Чтобы найти неизвестный делитель, нужно делимое разделить на частное.

Видео:Дружишь с банками? #математика #алгебра #арифметика #счет #репетитор #уравнение #логикаСкачать

Компоненты

Компонентами мы будем называть числа и переменные, входящие в равенство

Так, компонентами сложения являются слагаемые и сумма

Компонентами вычитания являются уменьшаемое, вычитаемое и разность

Компонентами умножения являются множимое, множитель и произведение

Компонентами деления являются делимое, делитель и частное

В зависимости от того, с какими компонентами мы будем иметь дело, будут применяться соответствующие правила нахождения неизвестных. Эти правила мы изучили в предыдущей теме. При решении уравнений желательно знать эти правило наизусть.

Пример 1. Найти корень уравнения 45 + x = 60

45 — слагаемое, x — неизвестное слагаемое, 60 — сумма. Имеем дело с компонентами сложения. Вспоминаем, что для нахождения неизвестного слагаемого, нужно из суммы вычесть известное слагаемое:

Вычислим правую часть, получим значение x равное 15

Значит корень уравнения 45 + x = 60 равен 15.

Чаще всего неизвестное слагаемое необходимо привести к виду при котором его можно было бы выразить.

Пример 2. Решить уравнение

Здесь в отличие от предыдущего примера, неизвестное слагаемое нельзя выразить сразу, поскольку оно содержит коэффициент 2. Наша задача привести это уравнение к виду при котором можно было бы выразить x

В данном примере мы имеем дело с компонентами сложения — слагаемыми и суммой. 2x — это первое слагаемое, 4 — второе слагаемое, 8 — сумма.

При этом слагаемое 2x содержит переменную x . После нахождения значения переменной x слагаемое 2x примет другой вид. Поэтому слагаемое 2x можно полностью принять за неизвестное слагаемое:

Теперь применяем правило нахождения неизвестного слагаемого. Вычитаем из суммы известное слагаемое:

Вычислим правую часть получившегося уравнения:

Мы получили новое уравнение 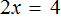. Теперь мы имеем дело с компонентами умножения: множимым, множителем и произведением. 2 — множимое, x — множитель, 4 — произведение

При этом переменная x является не просто множителем, а неизвестным множителем

Чтобы найти этот неизвестный множитель, нужно произведение разделить на множимое:

Вычислим правую часть, получим значение переменной x

Для проверки найденный корень отправим в исходное уравнение и подставим вместо x

Получили верное числовое равенство. Значит уравнение решено правильно.

Пример 3. Решить уравнение 3x + 9x + 16x = 56

Cразу выразить неизвестное x нельзя. Сначала нужно привести данное уравнение к виду при котором его можно было бы выразить.

Приведем подобные слагаемые в левой части данного уравнения:

Имеем дело с компонентами умножения. 28 — множимое, x — множитель, 56 — произведение. При этом x является неизвестным множителем. Чтобы найти неизвестный множитель, нужно произведение разделить на множимое:

Отсюда x равен 2

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Равносильные уравнения

В предыдущем примере при решении уравнения 3x + 9x + 16x = 56 , мы привели подобные слагаемые в левой части уравнения. В результате получили новое уравнение 28x = 56 . Старое уравнение 3x + 9x + 16x = 56 и получившееся новое уравнение 28x = 56 называют равносильными уравнениями, поскольку их корни совпадают.

Уравнения называют равносильными, если их корни совпадают.

Проверим это. Для уравнения 3x + 9x + 16x = 56 мы нашли корень равный 2 . Подставим этот корень сначала в уравнение 3x + 9x + 16x = 56 , а затем в уравнение 28x = 56 , которое получилось в результате приведения подобных слагаемых в левой части предыдущего уравнения. Мы должны получить верные числовые равенства

Согласно порядку действий, в первую очередь выполняется умножение:

Подставим корень 2 во второе уравнение 28x = 56

Видим, что у обоих уравнений корни совпадают. Значит уравнения 3x + 9x + 16x = 56 и 28x = 56 действительно являются равносильными.

Для решения уравнения 3x + 9x + 16x = 56 мы воспользовались одним из тождественных преобразований — приведением подобных слагаемых. Правильное тождественное преобразование уравнения позволило нам получить равносильное уравнение 28x = 56 , которое проще решать.

Из тождественных преобразований на данный момент мы умеем только сокращать дроби, приводить подобные слагаемые, выносить общий множитель за скобки, а также раскрывать скобки. Существуют и другие преобразования, которые следует знать. Но для общего представления о тождественных преобразованиях уравнений, изученных нами тем вполне хватает.

Рассмотрим некоторые преобразования, которые позволяют получить равносильное уравнение

Если к обеим частям уравнения прибавить одно и то же число, то получится уравнение равносильное данному.

Если из обеих частей уравнения вычесть одно и то же число, то получится уравнение равносильное данному.

Другими словами, корень уравнения не изменится, если к обеим частям данного уравнения прибавить (или вычесть из обеих частей) одно и то же число.

Пример 1. Решить уравнение

Вычтем из обеих частей уравнения число 10

Приведем подобные слагаемые в обеих частях:

Получили уравнение 5x = 10 . Имеем дело с компонентами умножения. Чтобы найти неизвестный сомножитель x , нужно произведение 10 разделить на известный сомножитель 5.

Отсюда .

Вернемся к исходному уравнению и подставим вместо x найденное значение 2

Получили верное числовое равенство. Значит уравнение решено правильно.

Решая уравнение мы вычли из обеих частей уравнения число 10 . В результате получили равносильное уравнение . Корень этого уравнения, как и уравнения так же равен 2

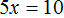
Пример 2. Решить уравнение 4(x + 3) = 16

Раскроем скобки в левой части равенства:

Вычтем из обеих частей уравнения число 12

Приведем подобные слагаемые в обеих частях уравнения:

В левой части останется 4x , а в правой части число 4

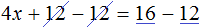
Получили уравнение 4x = 4 . Имеем дело с компонентами умножения. Чтобы найти неизвестный сомножитель x , нужно произведение 4 разделить на известный сомножитель 4

Отсюда

Вернемся к исходному уравнению 4(x + 3) = 16 и подставим вместо x найденное значение 1

Получили верное числовое равенство. Значит уравнение решено правильно.

Решая уравнение 4(x + 3) = 16 мы вычли из обеих частей уравнения число 12 . В результате получили равносильное уравнение 4x = 4 . Корень этого уравнения, как и уравнения 4(x + 3) = 16 так же равен 1

Пример 3. Решить уравнение

Раскроем скобки в левой части равенства:

Прибавим к обеим частям уравнения число 8

Приведем подобные слагаемые в обеих частях уравнения:

В левой части останется 2x , а в правой части число 9

В получившемся уравнении 2x = 9 выразим неизвестное слагаемое x

Отсюда

Вернемся к исходному уравнению и подставим вместо x найденное значение 4,5

Получили верное числовое равенство. Значит уравнение решено правильно.

Решая уравнение мы прибавили к обеим частям уравнения число 8. В результате получили равносильное уравнение . Корень этого уравнения, как и уравнения так же равен 4,5

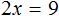
Следующее правило, которое позволяет получить равносильное уравнение, выглядит следующим образом

Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение равносильное данному.

То есть корень уравнения не изменится, если мы перенесем слагаемое из одной части уравнения в другую, изменив его знак. Это свойство является одним из важных и одним из часто используемых при решении уравнений.

Рассмотрим следующее уравнение:

Корень данного уравнения равен 2. Подставим вместо x этот корень и проверим получается ли верное числовое равенство

Получается верное равенство. Значит число 2 действительно является корнем уравнения .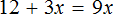

Теперь попробуем поэкспериментировать со слагаемыми этого уравнения, перенося их из одной части в другую, изменяя знаки.

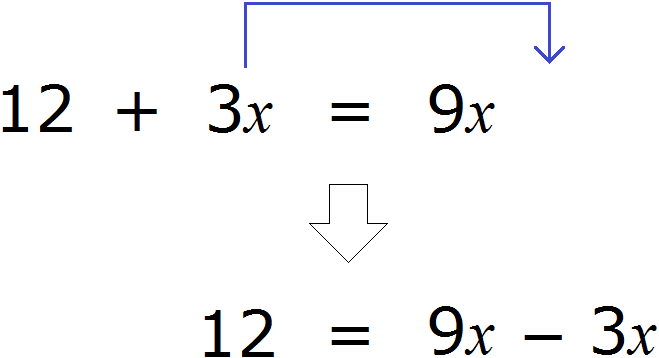
Например, слагаемое 3x располагается в левой части равенства. Перенесём его в правую часть, изменив знак на противоположный:

Получилось уравнение 12 = 9x − 3x . Приведем подобные слагаемые в правой части данного уравнения:

Имеем дело с компонентами умножения. Переменная x является неизвестным сомножителем. Найдём этот известный сомножитель:

Отсюда x = 2 . Как видим, корень уравнения не изменился. Значит уравнения 12 + 3x = 9x и 12 = 9x − 3x являются равносильными.

На самом деле данное преобразование является упрощенным методом предыдущего преобразования, где к обеим частям уравнения прибавлялось (или вычиталось) одно и то же число.

Мы сказали, что в уравнении 12 + 3x = 9x слагаемое 3x было перенесено в правую часть, изменив знак. В реальности же происходило следующее: из обеих частей уравнения вычли слагаемое 3x

Затем в левой части были приведены подобные слагаемые и получено уравнение 12 = 9x − 3x. Затем опять были приведены подобные слагаемые, но уже в правой части, и получено уравнение 12 = 6x.

Но так называемый «перенос» более удобен для подобных уравнений, поэтому он и получил такое широкое распространение. Решая уравнения, мы часто будем пользоваться именно этим преобразованием.

Равносильными также являются уравнения 12 + 3x = 9x и 3x − 9x = −12 . В этот раз в уравнении 12 + 3x = 9x слагаемое 12 было перенесено в правую часть, а слагаемое 9x в левую. Не следует забывать, что знаки этих слагаемых были изменены во время переноса

Следующее правило, которое позволяет получить равносильное уравнение, выглядит следующим образом:

Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю, то получится уравнение равносильное данному.

Другими словами, корни уравнения не изменятся, если обе его части умножить или разделить на одно и то же число. Это действие часто применяется тогда, когда нужно решить уравнение содержащее дробные выражения.

Сначала рассмотрим примеры, в которых обе части уравнения будут умножаться на одно и то же число.

Пример 1. Решить уравнение

При решении уравнений, содержащих дробные выражения, сначала принято упростить это уравнение.

В данном случае мы имеем дело именно с таким уравнением. В целях упрощения данного уравнения обе его части можно умножить на 8:

Мы помним, что для умножения дроби на число, нужно числитель данной дроби умножить на это число. У нас имеются две дроби и каждая из них умножается на число 8. Наша задача умножить числители дробей на это число 8

Теперь происходит самое интересное. В числителях и знаменателях обеих дробей содержится множитель 8, который можно сократить на 8. Это позволит нам избавиться от дробного выражения:

В результате останется простейшее уравнение

Ну и нетрудно догадаться, что корень этого уравнения равен 4

Вернемся к исходному уравнению и подставим вместо x найденное значение 4

Получается верное числовое равенство. Значит уравнение решено правильно.

При решении данного уравнения мы умножили обе его части на 8. В результате получили уравнение 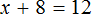. Корень этого уравнения, как и уравнения равен 4. Значит эти уравнения равносильны.

Множитель на который умножаются обе части уравнения принято записывать перед частью уравнения, а не после неё. Так, решая уравнение , мы умножили обе части на множитель 8 и получили следующую запись:

От этого корень уравнения не изменился, но если бы мы сделали это находясь в школе, то нам сделали бы замечание, поскольку в алгебре множитель принято записывать перед тем выражением, с которым он перемножается. Поэтому умножение обеих частей уравнения на множитель 8 желательно переписать следующим образом:

Пример 2. Решить уравнение

Умнóжим обе части уравнения на 15

В левой части множители 15 можно сократить на 15, а в правой части множители 15 и 5 можно сократить на 5

Перепишем то, что у нас осталось:

Раскроем скобки в правой части уравнения:

Перенесем слагаемое x из левой части уравнения в правую часть, изменив знак. А слагаемое 15 из правой части уравнения перенесем в левую часть, опять же изменив знак:

Приведем подобные слагаемые в обеих частях, получим

Имеем дело с компонентами умножения. Переменная x является неизвестным сомножителем. Найдём этот известный сомножитель:

Отсюда

Вернемся к исходному уравнению 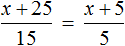и подставим вместо x найденное значение 5

Получается верное числовое равенство. Значит уравнение решено правильно. При решении данного уравнения мы умножили обе го части на 15 . Далее выполняя тождественные преобразования, мы получили уравнение 10 = 2x . Корень этого уравнения, как и уравнения 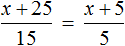равен 5 . Значит эти уравнения равносильны.

Пример 3. Решить уравнение

Умнóжим обе части уравнения на 3

В левой части можно сократить две тройки, а правая часть будет равна 18

Останется простейшее уравнение 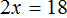. Имеем дело с компонентами умножения. Переменная x является неизвестным сомножителем. Найдём этот известный сомножитель:

Отсюда

Вернемся к исходному уравнению 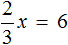и подставим вместо x найденное значение 9

Получается верное числовое равенство. Значит уравнение решено правильно.

Пример 4. Решить уравнение

Умнóжим обе части уравнения на 6

В левой части уравнения раскроем скобки. В правой части множитель 6 можно поднять в числитель:

Сократим в обеих частях уравнениях то, что можно сократить:

Перепишем то, что у нас осталось:

Раскроем скобки в обеих частях уравнения:

Воспользуемся переносом слагаемых. Слагаемые, содержащие неизвестное x , сгруппируем в левой части уравнения, а слагаемые свободные от неизвестных — в правой:

Приведем подобные слагаемые в обеих частях:

Теперь найдем значение переменной x . Для этого разделим произведение 28 на известный сомножитель 7

Вернемся к исходному уравнению 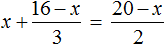и подставим вместо x найденное значение 4

Получилось верное числовое равенство. Значит уравнение решено правильно.

Пример 5. Решить уравнение

Раскроем скобки в обеих частях уравнения там, где это можно:

Умнóжим обе части уравнения на 15

Раскроем скобки в обеих частях уравнения:

Сократим в обеих частях уравнения, то что можно сократить:

Перепишем то, что у нас осталось:

Раскроем скобки там, где это можно:

Воспользуемся переносом слагаемых. Слагаемые, содержащие неизвестное, сгруппируем в левой части уравнения, а слагаемые, свободные от неизвестных — в правой. Не забываем, что во время переноса, слагаемые меняют свои знаки на противоположные:

Приведем подобные слагаемые в обеих частях уравнения:

Найдём значение x

В получившемся ответе можно выделить целую часть:

Вернемся к исходному уравнению и подставим вместо x найденное значение

Получается довольно громоздкое выражение. Воспользуемся переменными. Левую часть равенства занесем в переменную A , а правую часть равенства в переменную B

Наша задача состоит в том, чтобы убедиться равна ли левая часть правой. Другими словами, доказать равенство A = B

Найдем значение выражения, находящегося в переменной А.

Значение переменной А равно . Теперь найдем значение переменной B . То есть значение правой части нашего равенства. Если и оно равно , то уравнение будет решено верно

Видим, что значение переменной B , как и значение переменной A равно . Это значит, что левая часть равна правой части. Отсюда делаем вывод, что уравнение решено правильно.

Теперь попробуем не умножать обе части уравнения на одно и то же число, а делить.

Рассмотрим уравнение 30x + 14x + 14 = 70x − 40x + 42 . Решим его обычным методом: слагаемые, содержащие неизвестные, сгруппируем в левой части уравнения, а слагаемые, свободные от неизвестных — в правой. Далее выполняя известные тождественные преобразования, найдем значение x

Подставим найденное значение 2 вместо x в исходное уравнение:

Теперь попробуем разделить все слагаемые уравнения 30x + 14x + 14 = 70x − 40x + 42 на какое-нибудь число. Замечаем, что все слагаемые этого уравнения имеют общий множитель 2. На него и разделим каждое слагаемое:

Выполним сокращение в каждом слагаемом:

Перепишем то, что у нас осталось:

Решим это уравнение, пользуясь известными тождественными преобразованиями:

Получили корень 2 . Значит уравнения 15x + 7x + 7 = 35x − 20x + 21 и 30x + 14x + 14 = 70x − 40x + 42 равносильны.

Деление обеих частей уравнения на одно и то же число позволяет освобождать неизвестное от коэффициента. В предыдущем примере когда мы получили уравнение 7x = 14 , нам потребовалось разделить произведение 14 на известный сомножитель 7. Но если бы мы в левой части освободили неизвестное от коэффициента 7, корень нашелся бы сразу. Для этого достаточно было разделить обе части на 7

Этим методом мы тоже будем пользоваться часто.

Умножение на минус единицу

Если обе части уравнения умножить на минус единицу, то получится уравнение равносильное данному.

Это правило следует из того, что от умножения (или деления) обеих частей уравнения на одно и то же число, корень данного уравнения не меняется. А значит корень не поменяется если обе его части умножить на −1 .

Данное правило позволяет поменять знаки всех компонентов, входящих в уравнение. Для чего это нужно? Опять же, чтобы получить равносильное уравнение, которое проще решать.

Рассмотрим уравнение . Чему равен корень этого уравнения?

Прибавим к обеим частям уравнения число 5

Приведем подобные слагаемые:

А теперь вспомним про коэффициент буквенного выражения. Что же представляет собой левая часть уравнения 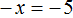. Это есть произведение минус единицы и переменной x

То есть минус, стоящий перед переменной x, относится не к самой переменной x , а к единице, которую мы не видим, поскольку коэффициент 1 принято не записывать. Это означает, что уравнение 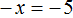на самом деле выглядит следующим образом:

Имеем дело с компонентами умножения. Чтобы найти х , нужно произведение −5 разделить на известный сомножитель −1 .

или разделить обе части уравнения на −1 , что еще проще

Итак, корень уравнения равен 5 . Для проверки подставим его в исходное уравнение. Не забываем, что в исходном уравнении минус стоящий перед переменной x относится к невидимой единице

Получилось верное числовое равенство. Значит уравнение решено верно.

Теперь попробуем умножить обе части уравнения на минус единицу:

После раскрытия скобок в левой части образуется выражение 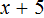, а правая часть будет равна 10

Корень этого уравнения, как и уравнения равен 5

Значит уравнения и равносильны.

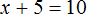
Пример 2. Решить уравнение

В данном уравнении все компоненты являются отрицательными. С положительными компонентами работать удобнее, чем с отрицательными, поэтому поменяем знаки всех компонентов, входящих в уравнение . Для этого умнóжим обе части данного уравнения на −1 .

Понятно, что от умножения на −1 любое число поменяет свой знак на противоположный. Поэтому саму процедуру умножения на −1 и раскрытие скобок подробно не расписывают, а сразу записывают компоненты уравнения с противоположными знаками.

Так, умножение уравнения на −1 можно записать подробно следующим образом:

либо можно просто поменять знаки всех компонентов:

Получится то же самое, но разница будет в том, что мы сэкономим себе время.

Итак, умножив обе части уравнения на −1 , мы получили уравнение . Решим данное уравнение. Из обеих частей вычтем число 4 и разделим обе части на 3

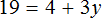
Когда корень найден, переменную обычно записывают в левой части, а её значение в правой, что мы и сделали.

Пример 3. Решить уравнение

Умнóжим обе части уравнения на −1 . Тогда все компоненты поменяют свои знаки на противоположные:

Из обеих частей получившегося уравнения вычтем 2x и приведем подобные слагаемые:

Прибавим к обеим частям уравнения единицу и приведем подобные слагаемые:

Приравнивание к нулю

Недавно мы узнали, что если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение равносильное данному.

А что будет если перенести из одной части в другую не одно слагаемое, а все слагаемые? Верно, в той части откуда забрали все слагаемые останется ноль. Иными словами, не останется ничего.

В качестве примера рассмотрим уравнение 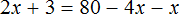. Решим данное уравнение, как обычно — слагаемые, содержащие неизвестные сгруппируем в одной части, а числовые слагаемые, свободные от неизвестных оставим в другой. Далее выполняя известные тождественные преобразования, найдем значение переменной x

Теперь попробуем решить это же уравнение, приравняв все его компоненты к нулю. Для этого перенесем все слагаемые из правой части в левую, изменив знаки:

Приведем подобные слагаемые в левой части:

Прибавим к обеим частям 77 , и разделим обе части на 7

Альтернатива правилам нахождения неизвестных

Очевидно, что зная о тождественных преобразованиях уравнений, можно не заучивать наизусть правила нахождения неизвестных.

К примеру, для нахождения неизвестного в уравнении мы произведение 10 делили на известный сомножитель 2

Но если в уравнении обе части разделить на 2 корень найдется сразу. В левой части уравнения в числителе множитель 2 и в знаменателе множитель 2 сократятся на 2. А правая часть будет равна 5

Уравнения вида мы решали выражая неизвестное слагаемое:

Но можно воспользоваться тождественными преобразованиями, которые мы сегодня изучили. В уравнении слагаемое 4 можно перенести в правую часть, изменив знак:

Далее разделить обе части на 2

В левой части уравнения сократятся две двойки. Правая часть будет равна 2. Отсюда .

Либо можно было из обеих частей уравнения вычесть 4. Тогда получилось бы следующее:

В случае с уравнениями вида удобнее делить произведение на известный сомножитель. Сравним оба решения:

Первое решение намного короче и аккуратнее. Второе решение можно значительно укоротить, если выполнить деление в уме.

Тем не менее, необходимо знать оба метода, и только затем использовать тот, который больше нравится.

Когда корней несколько

Уравнение может иметь несколько корней. Например уравнение x(x + 9) = 0 имеет два корня: 0 и −9 .

В уравнении x(x + 9) = 0 нужно было найти такое значение x при котором левая часть была бы равна нулю. В левой части этого уравнения содержатся выражения x и (x + 9) , которые являются сомножителями. Из законов умножения мы знаем, что произведение равно нулю, если хотя бы один из сомножителей равен нулю (или первый сомножитель или второй).

То есть в уравнении x(x + 9) = 0 равенство будет достигаться, если x будет равен нулю или (x + 9) будет равно нулю.

Приравняв к нулю оба этих выражения, мы сможем найти корни уравнения x(x + 9) = 0 . Первый корень, как видно из примера, нашелся сразу. Для нахождения второго корня нужно решить элементарное уравнение x + 9 = 0 . Несложно догадаться, что корень этого уравнения равен −9 . Проверка показывает, что корень верный:

Пример 2. Решить уравнение

Данное уравнение имеет два корня: 1 и 2. Левая часть уравнения является произведение выражений (x − 1) и (x − 2) . А произведение равно нулю, если хотя бы один из сомножителей равен нулю (или сомножитель (x − 1) или сомножитель (x − 2) ).

Найдем такое x при котором выражения (x − 1) или (x − 2) обращаются в нули:

Подставляем по-очереди найденные значения в исходное уравнение 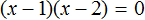и убеждаемся, что при этих значениях левая часть равняется нулю:

Когда корней бесконечно много

Уравнение может иметь бесконечно много корней. То есть подставив в такое уравнение любое число, мы получим верное числовое равенство.

Пример 1. Решить уравнение

Корнем данного уравнения является любое число. Если раскрыть скобки в левой части уравнения и привести подобные слагаемые, то получится равенство 14 = 14 . Это равенство будет получаться при любом x

Пример 2. Решить уравнение

Корнем данного уравнения является любое число. Если раскрыть скобки в левой части уравнения, то получится равенство 10x + 12 = 10x + 12. Это равенство будет получаться при любом x

Когда корней нет

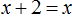
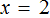
Случается и так, что уравнение вовсе не имеет решений, то есть не имеет корней. Например уравнение не имеет корней, поскольку при любом значении x , левая часть уравнения не будет равна правой части. Например, пусть . Тогда уравнение примет следующий вид

Пусть

Пример 2. Решить уравнение

Раскроем скобки в левой части равенства:

Приведем подобные слагаемые:

Видим, что левая часть не равна правой части. И так будет при любом значении y . Например, пусть y = 3 .

Буквенные уравнения

Уравнение может содержать не только числа с переменными, но и буквы.

Например, формула нахождения скорости является буквенным уравнением:

Данное уравнение описывает скорость движения тела при равноускоренном движении.

Полезным навыком является умение выразить любой компонент, входящий в буквенное уравнение. Например, чтобы из уравнения определить расстояние, нужно выразить переменную s .

Умнóжим обе части уравнения на t

В правой части переменные t сократим на t и перепишем то, что у нас осталось:

В получившемся уравнении левую и правую часть поменяем местами:

У нас получилась формула нахождения расстояния, которую мы изучали ранее.

Попробуем из уравнения определить время. Для этого нужно выразить переменную t .

Умнóжим обе части уравнения на t

В правой части переменные t сократим на t и перепишем то, что у нас осталось:

В получившемся уравнении v × t = s обе части разделим на v

В левой части переменные v сократим на v и перепишем то, что у нас осталось:

У нас получилась формула определения времени, которую мы изучали ранее.

Предположим, что скорость поезда равна 50 км/ч

А расстояние равно 100 км

Тогда буквенное уравнение примет следующий вид

Из этого уравнения можно найти время. Для этого нужно суметь выразить переменную t . Можно воспользоваться правилом нахождения неизвестного делителя, разделив делимое на частное и таким образом определить значение переменной t

либо можно воспользоваться тождественными преобразованиями. Сначала умножить обе части уравнения на t

Затем разделить обе части на 50

Пример 2. Дано буквенное уравнение 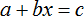. Выразите из данного уравнения x

Вычтем из обеих частей уравнения a

Разделим обе части уравнения на b

Теперь, если нам попадется уравнение вида a + bx = c , то у нас будет готовое решение. Достаточно будет подставить в него нужные значения. Те значения, которые будут подставляться вместо букв a, b, c принято называть параметрами. А уравнения вида a + bx = c называют уравнением с параметрами. В зависимости от параметров, корень будет меняться.

Решим уравнение 2 + 4x = 10 . Оно похоже на буквенное уравнение a + bx = c . Вместо того, чтобы выполнять тождественные преобразования, мы можем воспользоваться готовым решением. Сравним оба решения:

Видим, что второе решение намного проще и короче.

Для готового решения необходимо сделать небольшое замечание. Параметр b не должен быть равным нулю (b ≠ 0) , поскольку деление на ноль на допускается.

Пример 3. Дано буквенное уравнение 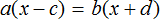. Выразите из данного уравнения x

Раскроем скобки в обеих частях уравнения

Воспользуемся переносом слагаемых. Параметры, содержащие переменную x , сгруппируем в левой части уравнения, а параметры свободные от этой переменной — в правой.

В левой части вынесем за скобки множитель x

Разделим обе части на выражение a − b

В левой части числитель и знаменатель можно сократить на a − b . Так окончательно выразится переменная x

Теперь, если нам попадется уравнение вида a(x − c) = b(x + d) , то у нас будет готовое решение. Достаточно будет подставить в него нужные значения.

Допустим нам дано уравнение 4(x − 3) = 2(x + 4) . Оно похоже на уравнение a(x − c) = b(x + d) . Решим его двумя способами: при помощи тождественных преобразований и при помощи готового решения:

Для удобства вытащим из уравнения 4(x − 3) = 2(x + 4) значения параметров a, b, c, d . Это позволит нам не ошибиться при подстановке:

Как и в прошлом примере знаменатель здесь не должен быть равным нулю (a − b ≠ 0) . Если нам встретится уравнение вида a(x − c) = b(x + d) в котором параметры a и b будут одинаковыми, мы сможем не решая его сказать, что у данного уравнения корней нет, поскольку разность одинаковых чисел равна нулю.

Например, уравнение 2(x − 3) = 2(x + 4) является уравнением вида a(x − c) = b(x + d) . В уравнении 2(x − 3) = 2(x + 4) параметры a и b одинаковые. Если мы начнём его решать, то придем к тому, что левая часть не будет равна правой части:

Пример 4. Дано буквенное уравнение 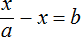. Выразите из данного уравнения x

Приведем левую часть уравнения к общему знаменателю:

Умнóжим обе части на a

В левой части x вынесем за скобки

Разделим обе части на выражение (1 − a)

Линейные уравнения с одним неизвестным

Рассмотренные в данном уроке уравнения называют линейными уравнениями первой степени с одним неизвестным.

Если уравнение дано в первой степени, не содержит деления на неизвестное, а также не содержит корней из неизвестного, то его можно назвать линейным. Мы еще не изучали степени и корни, поэтому чтобы не усложнять себе жизнь, слово «линейный» будем понимать как «простой».

Большинство уравнений, решенных в данном уроке, в конечном итоге сводились к простейшему уравнению, в котором нужно было произведение разделить на известный сомножитель. Таковым к примеру является уравнение 2 (x + 3) = 16 . Давайте решим его.

Раскроем скобки в левой части уравнения, получим 2 x + 6 = 16. Перенесем слагаемое 6 в правую часть, изменив знак. Тогда получим 2 x = 16 − 6. Вычислим правую часть, получим 2x = 10. Чтобы найти x , разделим произведение 10 на известный сомножитель 2. Отсюда x = 5.

Уравнение 2 (x + 3) = 16 является линейным. Оно свелось к уравнению 2x = 10 , для нахождения корня которого потребовалось разделить произведение на известный сомножитель. Такое простейшее уравнение называют линейным уравнением первой степени с одним неизвестным в каноническом виде. Слово «канонический» является синонимом слов «простейший» или «нормальный».

Линейное уравнение первой степени с одним неизвестным в каноническом виде называют уравнение вида ax = b.

Полученное нами уравнение 2x = 10 является линейным уравнением первой степени с одним неизвестным в каноническом виде. У этого уравнения первая степень, одно неизвестное, оно не содержит деления на неизвестное и не содержит корней из неизвестного, и представлено оно в каноническом виде, то есть в простейшем виде при котором легко можно определить значение x . Вместо параметров a и b в нашем уравнении содержатся числа 2 и 10. Но подобное уравнение может содержать и другие числа: положительные, отрицательные или равные нулю.

Если в линейном уравнении a = 0 и b = 0 , то уравнение имеет бесконечно много корней. Действительно, если a равно нулю и b равно нулю, то линейное уравнение ax = b примет вид 0x = 0 . При любом значении x левая часть будет равна правой части.

Если в линейном уравнении a = 0 и b ≠ 0 , то уравнение корней не имеет. Действительно, если a равно нулю и b равно какому-нибудь числу, не равному нулю, скажем числу 5, то уравнение ax = b примет вид 0x = 5 . Левая часть будет равна нулю, а правая часть пяти. А ноль не равен пяти.

Если в линейном уравнении a ≠ 0 , и b равно любому числу, то уравнение имеет один корень. Он определяется делением параметра b на параметр a

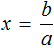
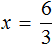
Действительно, если a равно какому-нибудь числу, не равному нулю, скажем числу 3 , и b равно какому-нибудь числу, скажем числу 6 , то уравнение примет вид .
Отсюда .

Существует и другая форма записи линейного уравнения первой степени с одним неизвестным. Выглядит она следующим образом: ax − b = 0 . Это то же самое уравнение, что и ax = b , но параметр b перенесен в левую часть с противоположным знаком. Такие уравнение мы тоже решали в данном уроке. Например, уравнение 7x − 77 = 0 . Уравнение вида ax − b = 0 называют линейным уравнением первой степени с одним неизвестным в общем виде.

В будущем после изучения рациональных выражений, мы рассмотрим такие понятия, как посторонние корни и потеря корней. А пока рассмотренного в данном уроке будет достаточным.