С помощью должным образом подобранного преобразования переменных
уравнение (4.3) можно преобразовать к наиболее простому <каноническому)виду, зависящему от типа этого уравнения.
Предположим, что функции ?(х, у) и Г|(х, у) дважды непрерывно дифференцируемы и якобиан преобразования (4.5) отличен от нуля в области D:
Тогда система (4.5) однозначно разрешима относительно х и у в некоторой области G точек (?, Г|), см. [3]. В предположении о двойной непрерывной дифференцируемости функции и(х, у), в области D вычислим ее производные по новым переменным ? и г по правилу дифференцирования сложной функции:
Подставляя найденные выражения для вторых производных в уравнение (4.2), получаем:
где
Легко убедиться в том, что
Из (4ЛЗ) следует, что преобразование независимых переменных (4.5) сохраняет тип уравнения (4.2) или (4.3).
Выберем преобразование (4.5), для которого часть уравнения
(4.2) , зависящая от старших производных, в новых переменных (?, г|) имеет наиболее простой вид. Тогда уравнение (4.2) принимает форму, которую называют канонической формой или каноническим видом данного уравнения.
Чтобы перейти к каноническому виду уравнения (4.2), найдем функции % = Ь> <х, у)и т| = t|(jc, у), для которых часть коэффициентов из (4.12) обращаются в нуль.
Из (4.12) видно, что для обращения в нуль коэффициентов аи и а22 в качестве функций % = ?,(х, у) и Г| = г(х, у) необходимо выбрать решения уравнения
Наряду с исходным уравнением в частных производных (4.2), введем в рассмотрение обыкновенное дифференциальное уравнение
которое называется характеристическим уравнением для уравнения
(4.2) , а его решения — характеристиками уравнения (4.2).
Теорема 4.1. Для того чтобы непрерывно дифференцируемая
функция z = Ф(*, у) была частным решением уравнения (4.14) в области ЛсК 2 , необходимо и достаточно, чтобы равенство ср(х, у) = С определяло в этой области общий интеграл обыкновенного дифференциального уравнения (4.15).
е D. Через эту точку проходит интегральная кривая у0 уравнения (4.15), для которой ф(х0, у0) = Q- Неявное уравнение кривой у0 имеет вид ф(х, у) = С0, а в явном виде она описывается функцией у = у(х, С0), причем у0 = у(х0, С0). С учетом правила дифференцирования неявной функции для всех точек интегральной кривой у0 имеем:
В частности, для х = х0 получим:
т.е. в точке (х0, у0) функция z = ф(х, у) удовлетворяет уравнению (4.14). В силу произвольности точки (х0, у0) е D приходим к выводу, что эта функция является решением уравнения (4.14) во всей области D. >
Таким образом, для преобразования уравнения (4.2) к каноническому виду необходимо найти общие интегралы характеристического уравнения (4.15). Рассмотрим случаи.
Случай 1. Пусть d = аг — аиап > 0 в области D, т.е. уравнение (4.2) относится к гиперболическому типу. Тогда характеристическое уравнение (4.15) эквивалентно совокупности обыкновенных дифференциальных уравнений:
Общие интегралы этих уравнений фДх, у) = Сх и ф2(х, у) = С2 определяют два семейства вещественных характеристик. Поскольку функции ф](х, у) и ф2(х, у) являются решениями уравнения (4.14), то, положив
в результате преобразования (4.5) с учетом (4.12) получим ап = а22 = = 0 в уравнении (4.11). В итоге это уравнение преобразуется к канонической форме уравнения гиперболического типа:
Замечание. Если вместо (4.18) использовать преобразование
то уравнение (4.2) примет вторую каноническую форму уравнения гиперболического типа:
Случай 2. Пусть d = af2 — апаи = 0 в области D, т.е. (4.2) — это уравнение параболического типа. Тогда характеристическое уравнение (4.15) принимает вид
и имеет только одно семейство характеристик ф, (х, у) = С. В преобразовании (4.18) полагаем ? = ?(х, у) = ф(х, у) и г| = ц(х, у) = ф2(х, у), где ф2(х, у) — произвольная дважды непрерывно дифференцируемая функция такая, что якобиан (4.6) преобразования (4.5) отличен от нуля в области D. Тогда в преобразованном уравнении (4.11) коэффициент аи =0, так как ? = ф(х, у) есть решение уравнения (4.14). Кроме того, ап = 0, поскольку d = а^2 — бпа12 = 0 (см. (4.13)) и аи = 0.
Таким образом, в результате преобразования (4.5) уравнение примет каноническую форму уравнения параболического типа:
Случай 3. Пусть d = а?2 — fin а и
Соотношение (4.24) представляет собой каноническую форму уравнения эллиптического типа.
Замечание. Приведение уравнения к каноническому виду связано с упрощением части уравнения (4.2), зависящей от старших (вторых) производных.
Для линейного уравнения (4.3) с постоянными коэффициентами возможно и дальнейшее упрощение, связанное с исключением из него первых производных.
Видео:§31.1 Приведение уравнения кривой к каноническому видуСкачать

Введем новую функцию v(?, г|), связанную с исходной неизвестной функцией м(^, т|) равенством
где а и р — неопределенные коэффициенты, за счет выбора которых достигается исключение первых производных и в преобразованном уравнении.
Найдем производные функции и
и с помощью соотношений (4.25), (4.26) перейдем к уравнению относительно функции v. После приведения подобных в этом уравнении приравниваем к нулю коэффициенты при и vn. Решив полученную систему двух уравнений, найдем значения аир.
Пример 4.3. Упростить уравнение
исключив из него первые производные.
2 + р 2 — 4а + 2(3 = -5. Окончательно получаем преобразованное уравнение:
Пример 4.4. Привести к каноническому виду уравнение
и провести его дальнейшее упрощение.
0 и уравнение относится к гиперболическому типу.
Характеристическое уравнение (4.15) имеет вид
Оно эквивалентно совокупности дифференциальных уравнений (4.17):
Отсюда находим характеристики 
Вычислим частные производные функций ^ и г:
Для упрощения дальнейших расчетов найдем по формулам (4.7)—
(4.10) и (4.29) выражения для всех производных, входящих в уравнение (4.27), и запишем слева от вертикальной черты коэффициенты при этих производных:
Теперь легко подсчитать коэффициенты, с которыми производные неизвестной функции входят в преобразованное уравнение:
Итак, мы нашли каноническую форму уравнения (4.27): 
Проведем дальнейшее упрощение уравнения с помощью преобразования (4.25). По формулам (4.26) находим:
После группировки коэффициентов при v^, v^, и v получаем:
откуда следует, что а = 2, (3 = -1. В итоге всех упрощений уравнение
(4.27) принимает вид
Замечание. Отметим, что результат примера 4.4 позволяет найти общее решение уравнения (4.27) в явном виде. Действительно, общий интеграл уравнения (4.30) имеет вид
где Ф и — произвольные один раз непрерывно дифференцируемые функции, см. (1.4).
Перейдем по формуле (4.25) при а = 2, (3 = -1 к исходной функции:
Возвращаясь к первоначальным переменным (х, у) по формулам
где Ф и Ч* — произвольные дважды непрерывно дифференцируемые функции.
Таким образом, приведение уравнений гиперболического типа к каноническому виду в некоторых случаях можно использовать как метод решения таких уравнений. 1>
Пример 4.5. Привести к каноническому виду уравнение
2 , за исключением точек осей координат, т.е. D = <(х, у) е R 2 | х * 0, у * о>.
В данном случае аи = х 2 , ап = ху, а22 = у 2 , поэтому d = 0 и уравнение относится к параболическому типу.
Характеристическое уравнение (4.15) имеет вид
Оно равносильно одному дифференциальному уравнению (4.17):
общий интеграл которого имеет вид ф = — = С. Делаем замену пере-
менных, полагая, например, г| = х:
Такая замена допустима, так как якобиан (4.6)
После применения формул (4.8)—(4.10) и приведения подобных членов получаем
Видео:Приведение ДУ 2 порядка в частных производных к каноническому видуСкачать

Выразим из (4.32) исходные переменные (х, у) через новые переменные (?, rj): х = г|, у = ^г). Подставив эти выражения в (4.33), окончательно найдем канонический вид уравнения (4.31):
Замечание. Отметим, что, используя полученный результат, можно найти общее решение уравнения (4.31) в явном виде. Для этого про-
интегрируем равенство Т)) = — по переменной Т| дважды. После первого интегрирования получим:
Интегрируя вторично, найдем:
где Ф и ? — произвольные непрерывные функции.
Возвратимся к старым переменным (х, у), используя равенства (4.32):
где Ф и — произвольные дважды непрерывно дифференцируемые функции.
Таким образом, приведение уравнений и параболического типа к каноническому виду в некоторых случаях можно применять как метод решения таких уравнений.
Пример 4.6. Привести к каноническому виду уравнение
2 ) 2 . Таким образом, d = 0 — (1 + у 2 ) 2 2 , поэтому уравнение относится к эллиптическому типу.
Характеристическое уравнение (4.15) имеет вид
Оно эквивалентно совокупности дифференциальных уравнений (4.23):
Отсюда находим характеристики 
Вычислим частные производные функций ?, и г:
Как и в примере 4.4, для упрощения дальнейших расчетов найдем по формулам (4.7)—(4.10) и (4.36) выражения для всех производных, входящих в уравнение (4.34), и запишем слева от вертикальной черты коэффициенты при этих производных:
Подсчитаем коэффициенты, с которыми производные неизвестной функции входят в преобразованное уравнение:
Итак, каноническая форма уравнения (4.34) имеет вид
Мы рассмотрели классификацию уравнений в частных производных второго порядка, зависящих от двух независимых переменных. Аналогично классифицируются уравнения, зависящие от большего числа переменных.
Обычно число независимых переменных в математических моделях физики и других наук не превосходит четырех (от одной до трех пространственных переменных и, возможно, время). В достаточно общем случае уравнения математической физики сводятся к одной из следующих канонических форм.
1. Математическое описание различных видов волн — упругих, звуковых, электромагнитных, а также других колебательных явлений обычно сводится к волновому уравнению (1.5):
относящемуся, как и уравнение колебаний струны (3.3), к гиперболическому типу, см. пример 4.1, а). Здесь с имеет физический смысл скорости волн в данной среде.
2. Процессы распространения тепла в однородном изотропном теле, а также явления диффузии описываются уравнением теплопроводности (1.6):
которое, как и уравнение (3.14), относится к параболическому типу (см. пример 4.1, б).
3. Математической моделью установившегося (стационарного) теплового процесса в однородной изотропной среде является уравнение Пуассона, см. (1.7) и (3.28):
Это уравнение описывает также потенциалы поля тяготения и электростатического поля в областях, где плотность распределения масс или зарядов пропорциональна f(x, у, z)•
При отсутствии источников тепла или масс и электрических зарядов уравнение Пуассона переходит в уравнение Лапласа (1.8):
Уравнения Пуассона и Лапласа относятся к эллиптическому типу, см. пример 4.1, в).
Как уже отмечалось в п. 1.3, перечисленные уравнения называют основными уравнениями математической физики. Они лежат в основе теории широкого круга физических явлений.
Приведение к каноническому виду линейных уравнений с частными производными второго порядка
Федеральное агентство по образованию
ИРКУТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Институт математики, экономики и информатики
Кафедра дифференциальных и интегральных уравнений
ПРИВЕДЕНИЕ К КАНОНИЧЕСКОМУ ВИДУ ЛИНЕЙНЫХ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ ВТОРОГО ПОРЯДКА
Приведение к каноническому виду линейных уравнений с частными производными 2-го порядка с двумя независимыми переменными …………………………………………………………………………
Видео:2. Приведение уравнений второго порядка к каноническому видуСкачать

1.1. Необходимый теоретический материал………………………..
1.2. Пример выполнения задачи1 (приведение к
каноническому виду уравнений гиперболического типа) .
1.3. Пример выполнения задачи 2 (приведение к
каноническому виду уравнений параболического типа)
1.4. Пример выполнения задачи 3 (приведение к
каноническому виду уравнений эллиптического типа) ..
1.5. Задачи для самостоятельного решения ………………….….
Упрощение группы младших производных
для уравнений второго порядка с постоянными коэффициентами
2.1. Необходимый теоретический материал …………………..
2.2. Пример выполнения задачи 4
2.3. Задачи для самостоятельного решения ……………………..
В настоящих методических указаниях изложен теоретический материал и на конкретных примерах разобрано приведение к каноническому виду линейных уравнений с частными производными второго порядка с двумя независимыми переменными для уравнений гиперболического, эллиптического и параболического типов.
Методические указания предназначены для студентов математических специальностей очной и заочной формы обучения.
§1. Приведение к каноническому виду линейных уравнений с частными производными 2-го порядка с двумя независимыми переменными.
Задача. Определить тип уравнения

и привести его к каноническому виду.
1.1. Необходимый теоретический материал.
I. Тип уравнения (1) определяется знаком выражения 
· если 
· если 
· если 
Уравнение (1) будет являться уравнением гиперболического, эллиптического, параболического типа в области D, если оно гиперболично, эллиптично, параболично в каждой точке этой области.
Уравнение (1) может менять свой тип при переходе из одной точки (области) в другую. Например, уравнение 



II. Чтобы привести уравнение к канонического виду, необходимо:
1. Определить коэффициенты 
2. Вычислить выражение 
3. Сделать вывод о типе уравнения (1) (в зависимости от знака выражения 
4. Записать уравнение характеристик:

5. Решить уравнение (2). Для этого:
а) разрешить уравнение (2) как квадратное уравнение относительно dy:

б) найти общие интегралы уравнений (3) (характеристики уравнения (1)):
· 
в случае уравнения гиперболического типа;
· 
в случае уравнения параболического типа;
· 
в случае уравнения эллиптического типа.
6. Ввести новые (характеристические) переменные 

· в случае уравнения гиперболического типа в качестве 

· в случае уравнения параболического типа в качестве 





· в случае уравнения эллиптического типа в качестве 

7. Пересчитать все производные, входящие в уравнение (1), используя правило дифференцирования сложной функции:





8. Подставить найденные производные в исходное уравнение (1) и привести подобные слагаемые. В результате уравнение (1) примет один из следующих видов:
· в случае уравнения гиперболического типа:

· в случае уравнения параболического типа:

· в случае уравнения эллиптического типа:

Видео:Приведение кривой второго порядка к каноническому виду. ПримерСкачать

1.2. Пример выполнения задачи 1.
Определить тип уравнения
и привести его к каноническому виду.
1. Определим коэффициенты 
2. Вычислим выражение 

3. 
4. Запишем уравнение характеристик:

5. Решим уравнение (9). Для этого:
а) разрешаем уравнение (9) как квадратное уравнение относительно dy: 



б) найдём общие интегралы уравнений (10) (характеристики уравнения (9)):
6. Введём характеристические переменные:
7. Пересчитаем производные, входящие в исходное уравнение.
Используя формулы (7), получим:
Здесь слева написаны коэффициенты уравнения (8) при соответствующих производных.
8. Собирая подобные слагаемые, получим:
Или после деления на -100 (коэффициент при 
Ответ. Уравнение (8) является уравнением гиперболического типа на всей плоскости XOY. Канонический вид
где
1.3. Пример выполнения задачи 2.
Определить тип уравнения
и привести его к каноническому виду.
1. Определим коэффициенты 
2. Вычислим выражение 

3. 
4. Запишем уравнение характеристик:

5. Решим уравнение (12). Для этого:
а) разрешаем уравнение (9) как квадратное уравнение относительно dy. Однако в этом случае левая часть уравнения является полным квадратом:


б) имеем только одно уравнение характеристик (13). Найдём его общий интеграл (уравнения параболического типа имеют только одно семейство вещественных характеристик):
6. Введём характеристические переменные: одну из переменных 
а в качестве 


7. Пересчитаем производные, входящие в исходное уравнение.
Используя формулы (7), получим:
Здесь слева написаны коэффициенты уравнения (11) при соответствующих производных.
8. Собирая подобные слагаемые, получим:
Функцию, стоящую в правой части уравнения (11) необходимо также выразить через характеристические переменные.
После деления на 25 (коэффициент при 
Ответ. Уравнение (11) является уравнением параболического типа на всей плоскости XOY. Канонический вид
где
1.4. Пример выполнения задачи 3.
Определить тип уравнения

и привести его к каноническому виду.
1. Определим коэффициенты 
2. Вычислим выражение 

3. 
4. Запишем уравнение характеристик:

5. Решим уравнение (15). Для этого:
а) разрешаем уравнение (15) как квадратное уравнение относительно dy: 
б) уравнения (16) – это пара комплексно-сопряженных уравнений. Они имеют пару комплексно-сопряженных общих интегралов. (Уравнения эллиптического типа не имеют вещественных характеристик)

6. Введём характеристические переменные как вещественную и мнимую части одного из общих интегралов (17):
7. Пересчитаем производные, входящие в исходное уравнение.
Видео:Семинар №9 "Приведение уравнения второго порядка к каноническому виду"Скачать

Используя формулы (7), получим:
Здесь слева написаны коэффициенты уравнения (14) при соответствующих производных.
8. Собирая подобные слагаемые, получим:
Или после деления на 4 (коэффициент при 

Ответ. Уравнение (14) является уравнением эллиптического типа на всей плоскости XOY. Канонический вид
где
1.5. Задачи для самостоятельного решения.
Определить тип уравнения и привести его к каноническому виду.










Определить тип уравнения и привести его к каноническому виду.
Определить тип уравнения и привести его к каноническому виду.
§2. Упрощение группы младших производных
для уравнений второго порядка с постоянными коэффициентами
2. 1. Необходимый теоретический материал
В самом общем виде линейное уравнение с частными производными второго порядка с двумя независимыми переменными имеет вид

Преобразованием независимых переменных группа старших производных уравнения может быть упрощена. Уравнение (1) приводится к одному из следующих видов
· в случае уравнения гиперболического типа:

· в случае уравнения параболического типа:

· в случае уравнения эллиптического типа:

Если коэффициенты исходного уравнения постоянны, то для дальнейшего упрощения уравнения любого типа нужно сделать замену неизвестной функции

где 





Чтобы реализовать замену (14) в уравнениях (11), (12), (13), необходимо пересчитать все производные, входящие в эти уравнения по формулам

Подробно рассмотрим этот процесс на примере уравнения гиперболического типа, т. е. уравнения (11). Пересчитаем производные, входящие в это уравнение, используя формулы (15).
Здесь слева расставлены соответствующие коэффициенты уравнения (11). Собирая подобные слагаемые, получим

В уравнении (16) приравняем к нулю коэффициенты при 
Откуда 


где 
2.2. Пример выполнения задачи 4
к каноническому виду и упростить группу младших производных.
9. Определим коэффициенты 
10. Вычислим выражение 

11. 
12. Запишем уравнение характеристик:

5. Решим уравнение (18). Для этого:
а) разрешаем уравнение (18) как квадратное уравнение относительно dy: 

б) найдём общие интегралы уравнений (19) (характеристики уравнения (17)):
6. Введём характеристические переменные:
13. Пересчитаем производные, входящие в исходное уравнение.
Используя формулы (7), получим:
Здесь слева написаны коэффициенты уравнения (17) при соответствующих производных.
14. Собирая подобные слагаемые, получим:

Теперь с помощью замены неизвестной функции (14)
упростим группу младших производных.
Пересчитаем производные, входящие в уравнение (20), используя формулы (15).
Видео:Видеоурок "Приведение к каноническому виду"Скачать

Здесь слева расставлены соответствующие коэффициенты уравнения (20). Собирая подобные слагаемые, получим

В уравнении (21) приравняем к нулю коэффициенты при 
Откуда 


Ответ. Уравнение (20) является уравнением эллиптического типа на всей плоскости XOY. Его канонический вид

где 
2.3. Задачи для самостоятельного решения
Задача 4. Привести уравнения к каноническому виду и упростить группу младших производных.










📽️ Видео
Приведение линейного уравнения в частных производных c постоянными коэфф--ми к каноническому виду.Скачать

Приводим уравнение кривой 2 порядка к каноническому видуСкачать

Кривые второго порядка. Парабола. Приведение к каноническому виду и чертежСкачать

13. Общие уравнения прямой в пространстве / приведение к каноническому видуСкачать

Привести квадратичную форму к каноническому видуСкачать
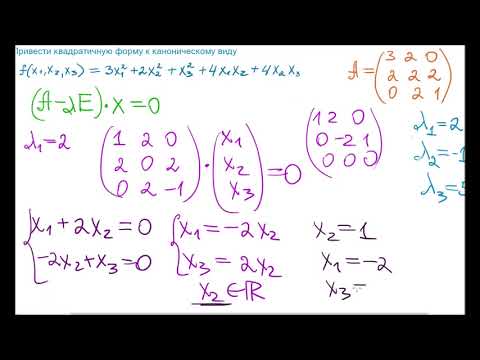
Кривые второго порядка. Эллипс. Приведение к каноническому виду и чертежСкачать

53. Приведение общего уравнения кривой к каноническому видуСкачать

Кривые второго порядка. Гипербола. Приведение к каноническому виду и чертежСкачать

Метод Лагранжа. Приведение квадратичной формы к каноническому и нормальному видамСкачать

1.2. Приведение к каноническому видуСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Семинар 6. Приведение уравнения кривой II порядка к каноническому видуСкачать


















































































































