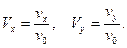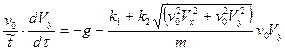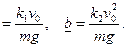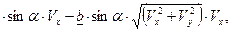На примере рассмотренной выше задачи покажем очень важный и полезный прием, популярный в физическом моделировании, называемый обезразмериванием. При решении задач мы пользуемся системой единиц (СИ), в которой далеко не все числовые значения находятся в удобном диапазоне. Кроме того, абсолютные значения величин дают мало информации для качественного понимания. Скорость 15 м/с – это много или мало? Все дело — по сравнению с чем.
Идея обезразмеривания заключается в переходе от абсолютных значений – расстояний, скоростей, времен (s, 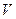
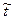
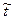
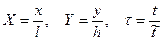
X, Y, 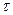
Введем безразмерные переменные для скоростей. Их естественно ввести, соотнося проекции скорости на оси х и у с начальной скоростью 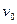
Теперь к безразмерным переменным нужно перейти в уравнениях систем (9)-(10).
Покажем, как перейти к безразмерным переменным в уравнениях системы (9) на примере второго уравнения этой системы.
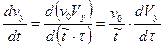
так как постоянный множитель можно вынести за знак производной.
Подставляя это в уравнение (9), получаем:
Подставляя 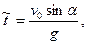
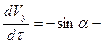
где a, b — безразмерные комбинации параметров, входящих в исходные уравнения,
a
Аналогично выполним обезразмеривание во всех уравнениях систем (9), (10) и получим:

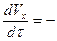
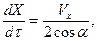
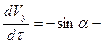
Начальные условия для безразмерных переменных имеют вид:
Важнейшая роль обезразмеривания – установление законов подобия. У изучаемого движения есть множество вариантов, определяемых наборами значений параметров, входящих в систему уравнений (9) — (10) и являющихся для них начальными условиями: 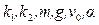
Закон подобия: Если мы изучаем два разных движения с разными размерными параметрами, но такие, что a, b, α – одинаковые, тогда движения будут качественно одинаковыми.
Число таких комбинаций обычно меньше числа размерных параметров (в данном случае вдвое), что также создает удобства при полном численном исследовании задачи. Наконец, как уже отмечалось, величины 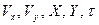
Прежде чем предпринимать численное моделирование, отметим, что при учете лишь линейной составляющей силы сопротивления модель допускает аналитическое решение.
Исследование задачи при произвольных значениях a, b, α будет выполняться на практике с помощью программы на языке Turbo Pascal.
- Приведение дифференциальных уравнений конвективного теплообмена и условий однозначности к безразмерному виду
- Приведение дифференциальных уравнений конвективного теплообмена и условий однозначности к безразмерному виду
- теория подобия. Теория, числа, уравнения подобия. Условия подобия процессов конвективного теплообмена
- 📺 Видео
Видео:Решение биквадратных уравнений. 8 класс.Скачать

Приведение дифференциальных уравнений конвективного теплообмена и условий однозначности к безразмерному виду


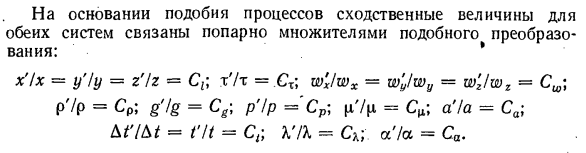






Видео:Приведение ДУ 2 порядка в частных производных к каноническому видуСкачать

Приведение дифференциальных уравнений конвективного теплообмена и условий однозначности к безразмерному виду
- Редукция дифференциальных уравнений конвекции Передача тепла к безразмерным формам и ясным условиям Чтобы применить на практике теорию подобия в случае конвективного теплообмена, описываемого системой дифференциальных уравнений и условиями единственности с большим числом переменных, необходимо сначала узнать число подобия, содержащееся в уравнении подобия. , Эти
системы дифференциальных уравнений, включая дифференциальные уравнения теплопередачи между твердыми телами в движущейся жидкости и внешней средой V, энергии или теплопроводности, движения вязких несжимаемых жидкостей (или уравнений Навье-Стокса) и непрерывности Числа, раскрывающие структуру. Хотя показанная система уравнений обеспечивает полное
математическое описание явления теплопередачи с условием единственности r, сталкивается с большими трудностями. Поскольку физические величины измерения могут быть связаны с безразмерными I-комплексами, число комплексов меньше, чем количество величин,
аналитическое решение этой системы Людмила Фирмаль
составляющих эти комплексы. Это значительно упрощает исследование физических процессов. Полученный безразмерный комплекс можно рассматривать как новую переменную c. Поэтому для получения числа сходств используется следующая формула: Уравнение движения вязкой жидкости Навье-Стокса (Dwx. „Dwx. Dwx. Dwx + w ‘- * r + 94rr f a * r v dx * n do * ^ dz * g ‘ (Для сокращения
вычислений уравнение Навье-Стокса дано только для осей ); Уравнение неразрывности жидкости _ | —_ Q •. (2b.13) И дг Уравнение энергии жидкости dt, а /. /. дт / дх, д4. дх / ог … Уравнение теплопередачи на границе между окружающей средой и твердым телом aAt- — X (dt / dx) CT. , (26-15) Напишите уравнения для двух похожих систем. «Процесс, который происходит в первой системе, описывается уравнениями (26-12) — (26-15). Процесс, который
происходит во второй системе, описывается тем же уравнением, что и процесс в первой системе. Но похожие значения имеют индекс (‘). / dsh’kh ;, dw’x, dwx дх дх’2 до’2 дз’1) dw ‘dw’ dw ‘ a / ‘,: / dt’, / dt ‘,, dt’ (a2 / ‘. dCh’.dCh’ от , / Dt, dt ‘, dt’ (a2 / ‘, dc’, dc ‘ /P|L.oh ‘At’ = -X ‘(dt’ / dx ‘) CT (26-19) Исходя из сходства процессов, одинаковые значения в обеих системах попарно связаны одинаковыми коэффициентами преобразования. x’lx = yChu = rChr = C < m7m = Cx w’x / wx = w’y / wy = w’z / wz = Сш р ‘/ р =
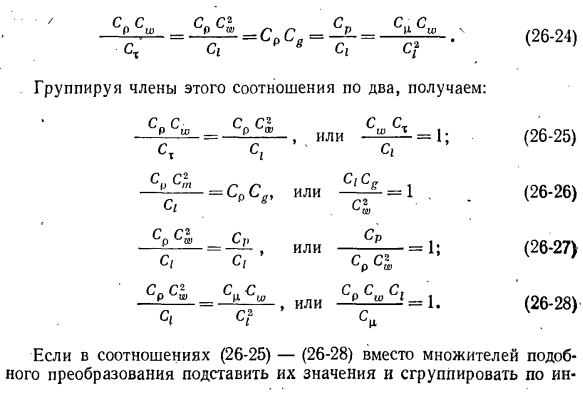
- Ср; g’lg = Cg-p’ / p = Сp] = C ^; a ‘/ a = Ca; M’lM = t’lt = Ct VA = Cx; ct’ / a = Ca. Выразите все переменные в уравнении (26-10) — (26-19) секунд • Система с коэффициентами пересчета, аналогичными первым системным переменным: CP Cu> l ^ x. CP C%> л /. , Dw St dt C / x dx y du 1 dg P * | C / ^ V ^ С? «Гr-Cr> -C’L ^ Группировка терминов в этих отношениях на две части: = Или кт с, с, = 1; = 1. C? P-g g или c, см cg Ci Ci C; или вода s, «C / ‘ср. C» CQ Cw или CP N Ci s? «» В соотношениях (26-25) — (26-28) вместо таких коэффициентов преобразования
сгруппируйте эти значения по индексу, чтобы получить следующий номер сходства. Но — то же самое; • (26-29) Fr = то же самое; (26-30) w2 ‘4 * и = — £ — = — ^ — = то же самое; (26-31). Low rou2 Re — ^ — = — ^ = То же самое, (26-32) V. v Где Ho — число гидродинамических синхроний и характеризует скорость изменения поля скоростей движущейся жидкости. Fr — число Фруда, которое определяет отношение инерции к гравитации. Она является числом Эйлера, которое характеризует
отношение силы давления к силе инерции. Re — число Рейнольдса. Это отношение силы инерции к силе вязкости и определяет характер потока жидкости. сходства двух или более систем. Для похожих точек они имеют одинаковое значение. Из уравнений энергии (26-14) и (26-22) мы имеем следующее соотношение: Или • (26-33) ct cf c? • CULCL = C ± CL) или С * СГ = к (2б.34) Cl Cl Ca Подстановка
Числа подобия Ho, Fr, Eu и Re используются для изучения гидродинамического Людмила Фирмаль
этих значений вместо аналогичных коэффициентов преобразования и деление переменной дает следующий номер подобия: То же, что и выше ;-( 26-35) rol- * , Pe = —- идем, • (26-36) Но где Fo — это число Фурье, мера тепловой одновременности, которая характеризует взаимосвязь между скоростью изменения температурного поля, физическими параметрами и размером тела. Re — число Пекле, число подобия
конвективного теплообмена. Подставляя значение, равное -A / sr, в число Fe вместо коэффициента термодиффузии a и умножая числитель и знаменатель на избыточную температуру ft, Pe = т.е. ■ (л / *) * Число подобия характеризует тепло, передаваемое конвекцией, а знаменатель характеризует тепло, передаваемое теплопроводностью. Из уравнений теплопередачи (26-15) и (26-23) получается следующее соотношение: _ _ C, C, C s, ct = или -4- ^ = 1. , (26-37) H ck После
преобразования и разделения переменных, Nu = — = то же самое, — (26-38) Nu — это число Нуссельта, которое характеризует конвективный теплообмен между жидкой и твердой поверхностями. Число Нуссельта определяется тем же значением, что и число Био, но число Nu содержит теплопроводность теплоносителя, а число Bi содержит теплопроводность твердого тела. Числа Fo, Pe и Nu используются для определения термического сходства двух или более систем. Для похожих точек они имеют одинаковое значение. Разделив число Pe
на число Re, получим новое число Pr. Pr = Pe / Re = v / a, (26-39) Где Pr — число Прандтля, определяющее физические свойства жидкости. Число Pe может быть выражено как произведение чисел Re и Pr: Pe = Re. Pr = (wl / ) (v / a) = wl / a. (26-40) При изучении теплообмена в свободном потоке жидкости учитывается число Фруда, но значение скорости w, которое очень трудно измерить, должно быть исключено. Для этого умножьте Fr на Re2. Ga = Fr • Re2 = идерри, (26-41) Где -Ga — число Галилея, которое характеризует отношение силы тяжести к
молекулярному трению. • Умножьте полученное число Ga на симплекс (p-p0) / po. Где p и p0 ‘- плотность жидкости в двух точках и получают новое число. A L AR • & 1 * DR. / ОС ЛОХ Ar является архимедовым числом, определяющим условия свободного движения среды. Симплекс (p-Po) / p заменяется на <W, если плотность жидкости изменяется из-за разницы в температуре в различных точках [p = p0 x X (1-PAO). Где (3 — коэффициент объемного
расширения) среды (когда газ р = 1/7). В этом случае номер Архимеда меняется на новый номер. Cr = L ^, (26-43) Здесь Gr — число Грасгофа, которое характеризует отношение подъемной силы, вызванной разницей между плотностью жидкости и силой молекулярного трения. Числа подобия Fr, Ga, Ar и Gr идентичны. Это те же четыре типа.




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:Приведение уравнений в частных производных к безразмерному виду.Скачать

теория подобия. Теория, числа, уравнения подобия. Условия подобия процессов конвективного теплообмена
| Название | Условия подобия процессов конвективного теплообмена |
| Анкор | теория подобия |
| Дата | 03.06.2021 |
| Размер | 220.5 Kb. |
| Формат файла |  |
| Имя файла | Теория, числа, уравнения подобия .ppt |
| Тип | Документы #213378 |
| Подборка по базе: Моделирование процессов упругого и неупругого ударов (1).pdf, АВТОМАТИЗАЦИЯ ХИМИКО-ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ.pdf, Глава 22. Вождение автомобиля в сложных условиях [1963 Вокрачко , Определение основных параметров производственного и технологичес, Теория информационных процессов и систем.docx, Приказ Минобр № 957 от 14.08.2013 г. — порядок и условия при лик, Моделирование экономических процессов.docx, моделирование экономических процессов.docx, 5. Технические условия на выполнения ручных работ.docx, Тушение пожаров в неблагоприятных климатических условиях (лек).d Условия подобия процессов конвективного теплообмена Если систему дифференциальных уравнений и граничные условия привести к безразмерному виду, то число влияющих факторов формально сократится, например число (критерий) Условия подобия физических явлений Если модель изготовлена в масштабе = 1/10, то для одной и той же жидкости на модели и натуре, для соблюдения условий подобия необходимо, чтобы отношение скоростей было = 10, что не всегда можно обеспечить. Безразмерное дифференциальное уравнение теплоотдачи Выразим размерные величины через безразмерные и масштабы отнесения, выбранные из условий однозначности, подставим их в дифференциальные уравнения и граничные условия. Тогда дифференциальное уравнение теплоотдачи примет вид: Дифференциальное уравнение энергии для стационарного режима имеет вид: Безразмерное дифференциальное уравнение энергии Умножим обе части уравнения (3) на Приведение к безразмерному виду уравнения движения Дифференциальное уравнение движения Навье-Стокса в проекции на ось х для стационарного режима: Числа подобия Рейнольдса, Грасгофа, Эйлера После сокращений имеем: (6) Безразмерное дифференциальное уравнение сплошности (неразрывности) Тогда безразмерное дифференциальное уравнение движения Безразмерные система уравнений и граничные условия Безразмерная система дифференциальных уравнений конвективного теплообмена: Преобразуем число Пекле следующим образом: Общий вид решений конвективной теплоотдачи в безразмерном виде Каждый определяемый критерий подобия является функцией определяющих: Подобными называются явления, которые имеют одинаковую физическую природу и описываются одинаковыми по форме и по содержанию уравнениями. II и III теоремы подобия физических явлений II теорема – решение дифференциального уравнения Для геометрического подобия необходимо равенство отношений сходственных сторон: — константа геометрического подобия. константа теплового константа кинема- подобия; тического подобия. 📺 Видео18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать  ДУ Уравнения, не разрешенные относительно производнойСкачать  6-1. Уравнение теплопроводностиСкачать  Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать  Приведение линейного уравнения в частных производных c постоянными коэфф--ми к каноническому виду.Скачать  Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать  Урок 133. Закон Бернулли. Уравнение БернуллиСкачать  6. Особые решения ДУ первого порядкаСкачать  Как решить симметрическое уравнение | Сведение к квадратному | Замена переменнойСкачать  Модели на основе дифференциальных уравнений с запаздыванием.Скачать  определение коэффициентов и свободных членов канонических уравнений. Решение канонического уравненияСкачать  Телеграфные уравнения. НормированиеСкачать  Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать  Уравнение дежавюСкачать  Уравнение из МФТИ Эпичный косякСкачать  Дифференциальные уравнения, 2 урок, Дифференциальные уравнения с разделяющимися переменнымиСкачать  Решение систем уравнений методом подстановкиСкачать  |