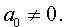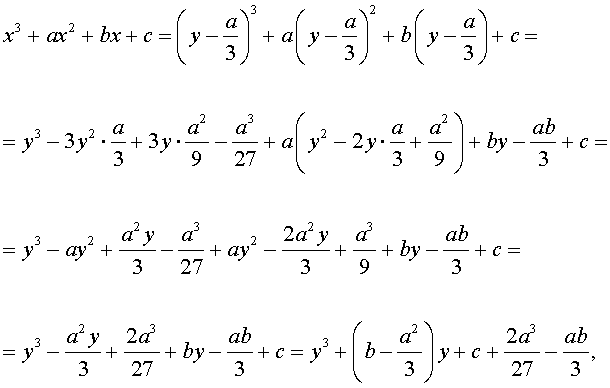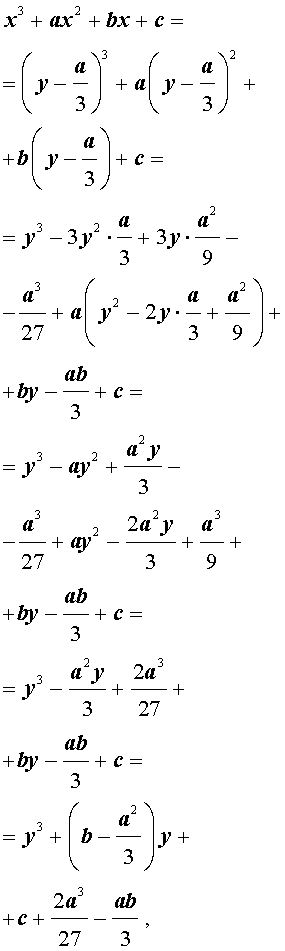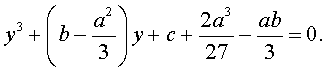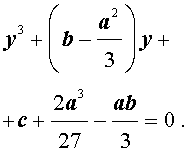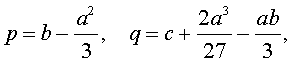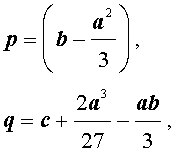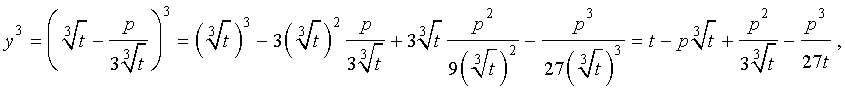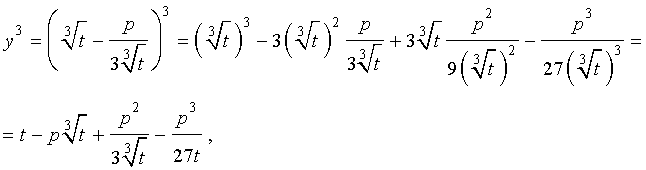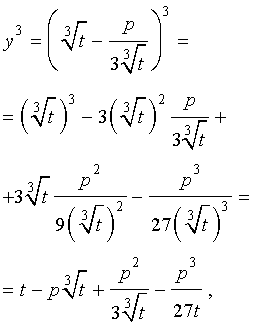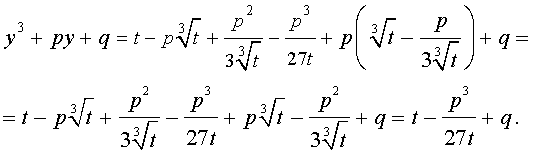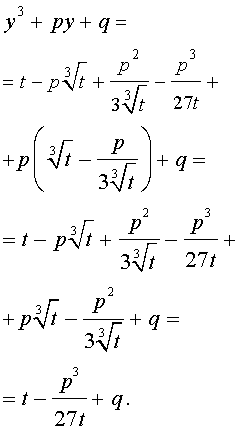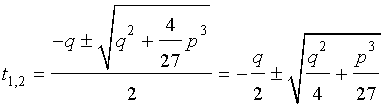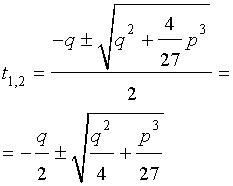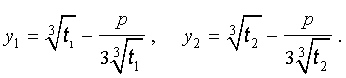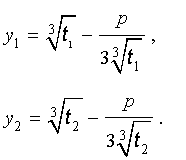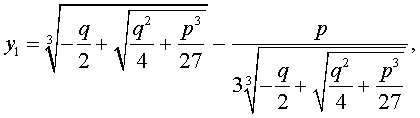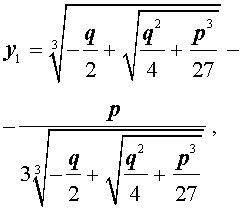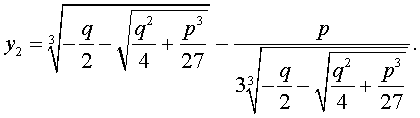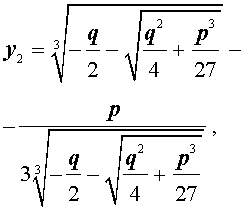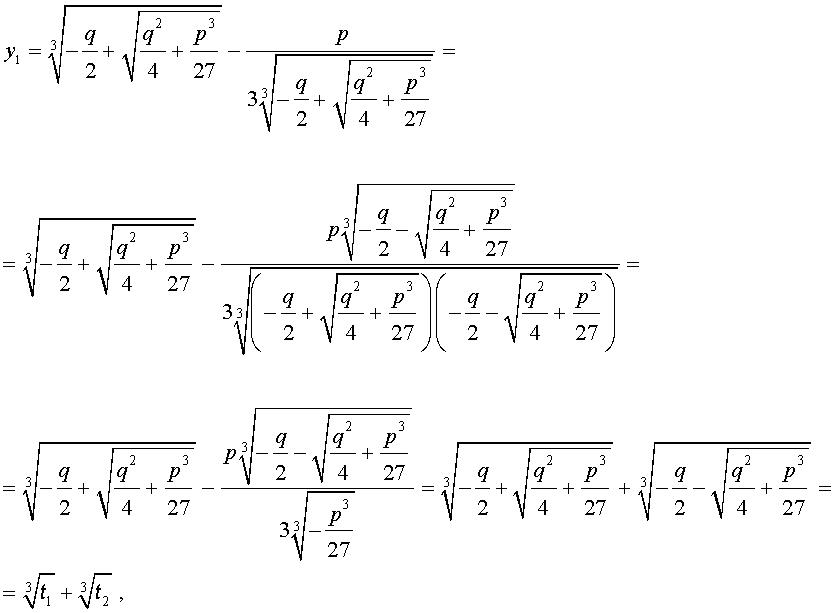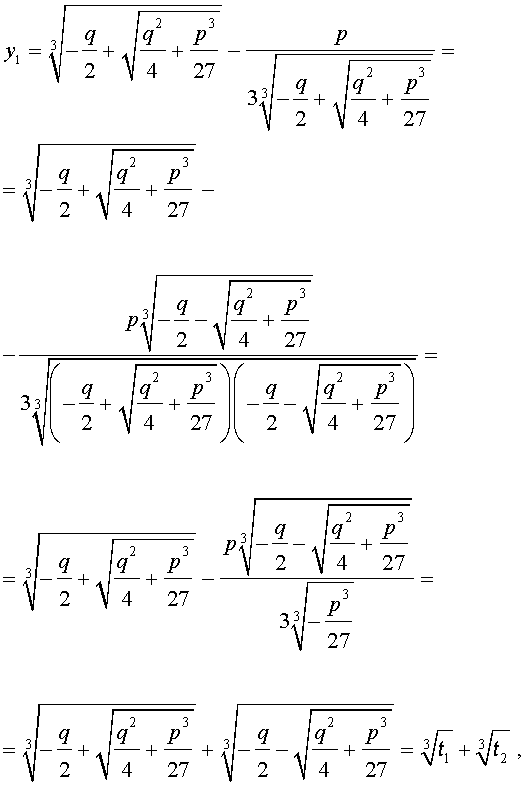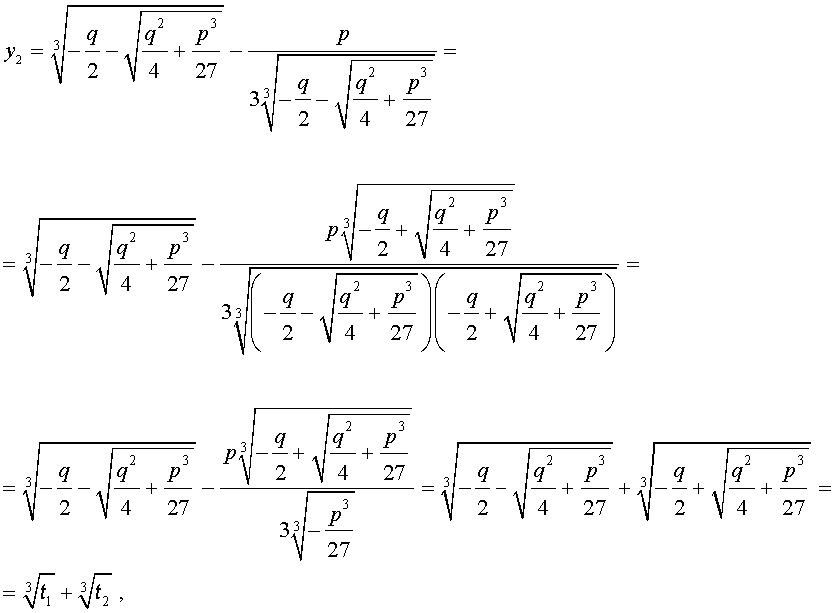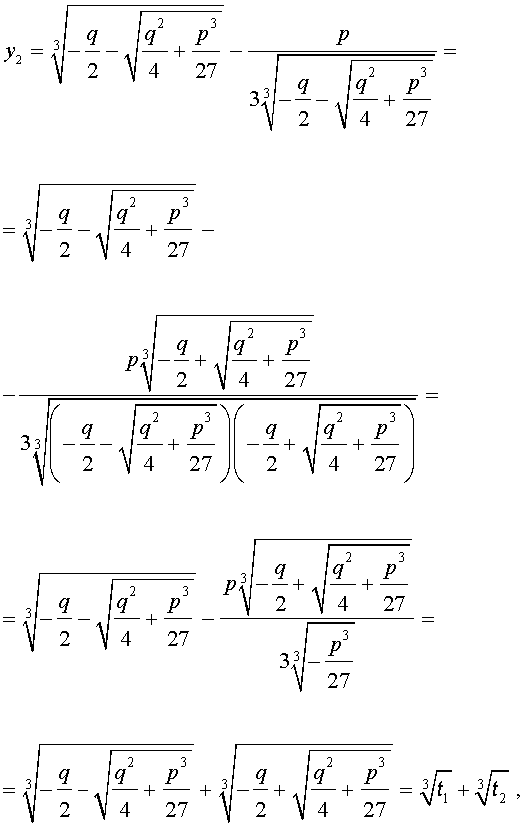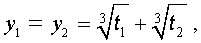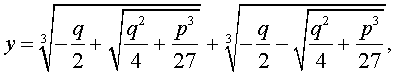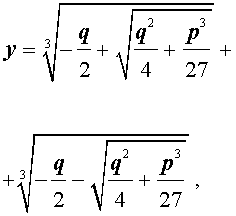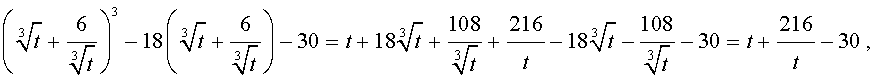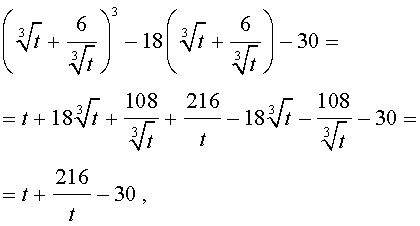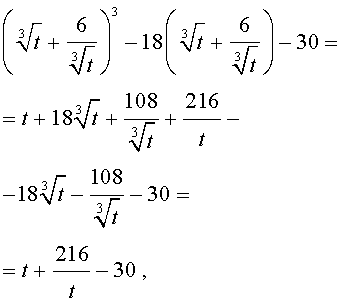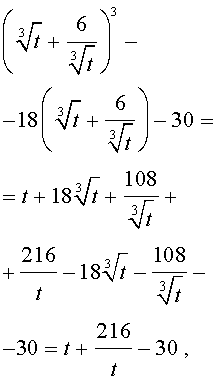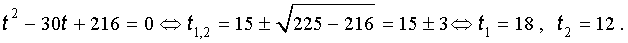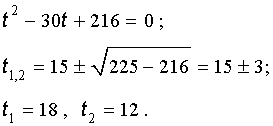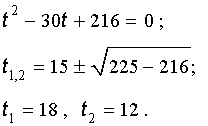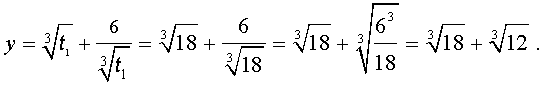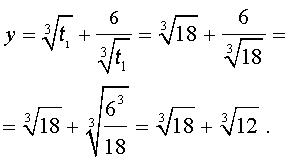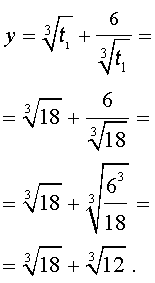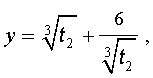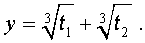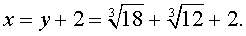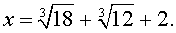 Схема метода Кардано |
| Приведение кубических уравнений к трехчленному виду |
| Сведение трёхчленных кубических уравнений к квадратным уравнениям при помощи метода Никколо Тартальи |
| Формула Кардано |
| Пример решения кубического уравнения |
- Схема метода Кардано
- Приведение кубических уравнений к трехчленному виду
- Сведение трёхчленных кубических уравнений к квадратным уравнениям при помощи метода Никколо Тартальи
- Формула Кардано
- Пример решения кубического уравнения
- Приведение кубического уравнения к каноническому виду
- Решения кубических уравнений с вещественными коэффициентами. Универсальные методы. Дискриминант кубического уравнения. Формула Виета для кубического уравнения.
- Решения кубических уравнений с вещественными коэффициентами. Универсальные методы. Дискриминант кубического уравнения. Формула Виета для кубического уравнения.
- Корни кубического уравнения. Нахождение корней (решение) кубического уравнения.
- 🎥 Видео
Видео:§31.1 Приведение уравнения кривой к каноническому видуСкачать
Схема метода Кардано
Целью данного раздела является вывод формулы Кардано для решения уравнений третьей степени ( кубических уравнений )
| a0x 3 + a1x 2 + + a2x + a3= 0, | (1) |
где a0, a1, a2, a3 – произвольные вещественные числа, 
Вывод формулы Кардано состоит из двух этапов.
На первом этапе кубические уравнения вида (1) приводятся к кубическим уравнениям, у которых отсутствует член со второй степенью неизвестного. Такие кубические уравнения называют трёхчленными кубическими уравнениями .
На втором этапе трёхчленные кубические уравнения решаются при помощи сведения их к квадратным уравнениям.
Видео:Кубическое уравнение (каконическая форма)Скачать
Приведение кубических уравнений к трехчленному виду
Разделим уравнение (1) на старший коэффициент a0 . Тогда оно примет вид
| x 3 + ax 2 + bx + c = 0, | (2) |
где a, b, c – произвольные вещественные числа.
Заменим в уравнении (2) переменную x на новую переменную y по формуле:
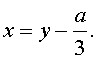 | (3) |
то уравнение (2) примет вид
В результате уравнение (2) примет вид
Если ввести обозначения
то уравнение (4) примет вид
| y 3 + py + q= 0, | (5) |
где p, q – вещественные числа.
Уравнения вида (5) и являются трёхчленными кубическими уравнениями , у которых отсутствует член со второй степенью неизвестного.
Первый этап вывода формулы Кардано завершён.
Видео:13. Общие уравнения прямой в пространстве / приведение к каноническому видуСкачать
Сведение трёхчленных кубических уравнений к квадратным уравнениям при помощи метода Никколо Тартальи
Следуя методу, примененому Никколо Тартальей (1499-1557) для решения трехчленных кубических уравнений, будем искать решение уравнения (5) в виде
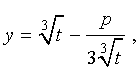 | (6) |
где t – новая переменная.
то выполнено равенство:
Следовательно, уравнение (5) переписывается в виде
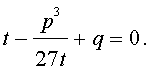 | (7) |
Если теперь уравнение (7) умножить на t , то мы получим квадратное уравнение относительно t :
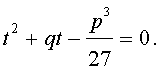 | (8) |
Видео:2. Приведение уравнений второго порядка к каноническому видуСкачать
Формула Кардано
Решение уравнения (8) имеет вид:
В соответствии с (6), отсюда вытекает, что уравнение (5) имеет два решения:
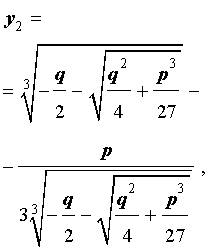
В развернутой форме эти решения записываются так:
Покажем, что, несмотря на кажущиеся различия, решения (10) и (11) совпадают.
С другой стороны,
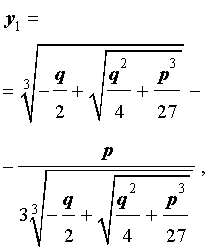
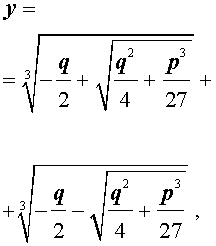
и для решения уравнения (5) мы получили формулу
которая и называется «Формула Кардано» .
Замечание . Поскольку у каждого комплексного числа, отличного от нуля, существуют три различных кубических корня, то, для того, чтобы избежать ошибок при решении кубических уравнений в области комплексных чисел, рекомендуется использовать формулу Кардано в виде (10) или (11).
Видео:Семинар №9 "Приведение уравнения второго порядка к каноническому виду"Скачать
Пример решения кубического уравнения
Пример . Решить уравнение
| x 3 – 6x 2 – 6x – 2 = 0. | (13) |
Решение . Сначала приведем уравнение (13) к трехчленному виду. Для этого в соответствии с формулой (3) сделаем в уравнении (13) замену
| x = y + 2. | (14) |
Следовательно, уравнение (13) принимает вид
| y 3 – 18y – 30 = 0. | (15) |
Теперь в соответствии с формулой (6) сделаем в уравнении (15) еще одну замену
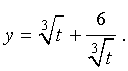 | (16) |
то уравнение (15) примет вид
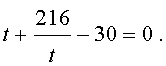 | (17) |
Далее из (17) получаем:
Отсюда по формуле (16) получаем:
Заметим, что такое же, как и в формуле (18), значение получилось бы, если бы мы использовали формулу
или использовали формулу
Далее из равенства (18) в соответствии с (14) получаем:
Таким образом, мы нашли у уравнения (13) вещественный корень
Замечание 1 . У уравнения (13) других вещественных корней нет.
Замечание 2 . Поскольку произвольное кубическое уравнение в комплексной области имеет 3 корня с учетом кратностей, то до полного решения уравнения (13) остается найти еще 2 корня. Эти корни можно найти разными способами, в частности, применив вариант формулы Кардано для области комплексных чисел. Однако применение такого варианта формулы Кардано значительно выходит за рамки курса математики даже специализированных математических школ.
Видео:53. Приведение общего уравнения кривой к каноническому видуСкачать
Приведение кубического уравнения к каноническому виду
| Коэффиценты кубического уравнения |
| Исходное кубическое уравнение |
| Приведенное кубическое уравнение |
Решаем задачу приведения произвольного кубического уравнения к каноническому виду.
к каноническому виду типа.
Есть широко известные формулы приведения, которые приведены ниже.
Чем они сложны? Тем, что при комплексных коэффицентах нам надо вычислять комплексное выражение, в котором легко ошибится.
Бот использует собственный метод расчета коэффицентов приведенного уравнения. Премущество видно на ниже приведенных примерах
Преобразуем в канонический вид уравнение
Введем в поле ввода коэффиценты
| Исходное кубическое уравнение |
| Приведенное кубическое уравнение |
Еще один пример
| Исходное кубическое уравнение |
| Приведенное кубическое уравнение |
Пример с комплексными коэффицентами
| Исходное кубическое уравнение |
| Приведенное кубическое уравнение |
Как видите быстро и легко рассчитываются коэфициенты проивзольного комплексного уравнения.
Проверка показывает, что преобразование происходит корректно.
Видео:Самый простой способ решить кубическое уравнениеСкачать
Решения кубических уравнений с вещественными коэффициентами. Универсальные методы. Дискриминант кубического уравнения. Формула Виета для кубического уравнения.
Видео:Приведение ДУ 2 порядка в частных производных к каноническому видуСкачать
Решения кубических уравнений с вещественными коэффициентами. Универсальные методы. Дискриминант кубического уравнения. Формула Виета для кубического уравнения.
Кубическим уравнением называется уравнение вида
- ax 3 + bx 2 + cx +d = 0 , (1)
- где a, b,c ,d — постоянные коэффициенты, а х — переменная.
Мы рассмотрим случай, когда коэффициенты являются веществеными числами.
Корни кубического уравнения. Нахождение корней (решение) кубического уравнения.
Число х называется корнем кубического уравнения (1), если при его подстановке уравнение (1) обращается в верное равенство.
Кубическое уравнение имеет не более трех корней (над комплексным полем всегда три корня, с учетом кратности) . И всегда имеет хотя бы 1 (вещественный) корень. Все возможные случаи состава корней легко определить с помощью знака дискриминанта кубического уравнения, т.е.:
Δ= -4b 3 d + b 2 c 2 — 4ac 3 + 18abcd — 27a 2 d 2 (Да, это дискриминант кубического уравнения)
Итак, возможны только 3 следующих случая:
- Δ > 0 — тогда уравнение имеет 3 различных корня. (Для продвинутых — три различных вещественных корня)
- Δ 3 + py + q = 0 (2)
К такому виду можно привести любое кубическое уравнение вида (1) с помощью следующей замены:
- x= y — b/3a (3)
- p= — b 2 /3a 2 + c/a
- q= 2b 3 /27a 3 — bc/3a 2 + d/a
Итак, приступим к вычислению корней. Найдем следующие величины:
Дискриминант уравнения (2) в этом случае равен
Дискриминант исходного уравнения (1) будет иметь тот же знак , что и вышеуказанный дискриминант. Корни уравнения (2) выражаются следующим образом:
Соответственно, если Q>0, то уравнения (2) и (1) будут иметь лишь 1 (вещественный) корень, y1. Подставим его в (3) и найдем х для уравнения (1). (если вас интересуют также мнимые корни, то просто вычислите еще и y2, y3 и подставьте их в (3).
Если Q 3 + ax 2 + bx +c = 0 (4)
Очевидно, любое уравнение вида (1) можно привести к виду (4), просто поделив его на коэффициент а.
Итак, алгоритм применения этой формулы:
3. a) Если S>0, то вычисляем
И наше уравнение имеет 3 корня (вещественных):
Тогда единственный корень (вещественный): x1= -2sgn(R)*|Q| 1/2 *ch(φ) — a/3
Для тех, кого интересуют также и мнимые корни:
- ch(x)=(e x +e -x )/2
- Arch(x) = ln(x + (x 2 -1) 1/2 )
- sh(x)=(e x -e -x )/2
- sgn(x) — знак х
в) Если S=0,то уравнение имеет меньше трех различных решений:
Консультации и техническая
поддержка сайта: Zavarka Team
🎥 Видео
✓ Как решать кубические уравнения. Формула Кардано | Ботай со мной #025 | Борис ТрушинСкачать
Видеоурок "Приведение к каноническому виду"Скачать
Приведение кривой второго порядка к каноническому виду. ПримерСкачать
Каноническое уравнение прямой в пространстве Преход от общего уравненияСкачать
КАК РЕШАТЬ КУБИЧЕСКИЕ УРАВНЕНИЯ | Разбираем на конкретном примереСкачать
Кубическое уравнение (парад подстановок)Скачать
Привести квадратичную форму к каноническому видуСкачать
Последовательность Падована и кубическое уравнениеСкачать
ОГЭ №21 Как решать кубическое уравнение x^3+4x^2-9x-36=0 Группировка Деление многочлена столбикомСкачать
Приводим уравнение кривой 2 порядка к каноническому видуСкачать
УМФ, 20.10.2021, приведение уравнений к каноническому видуСкачать
КУБИЧЕСКИЕ УРАВНЕНИЯ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать
