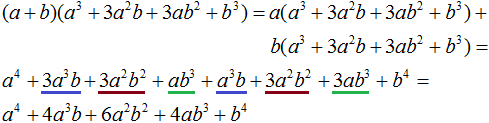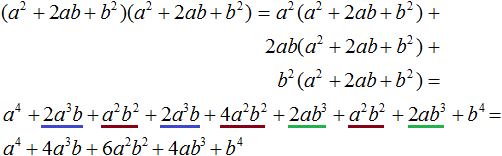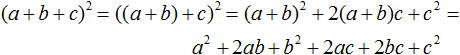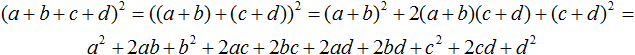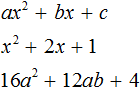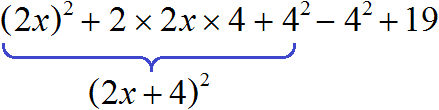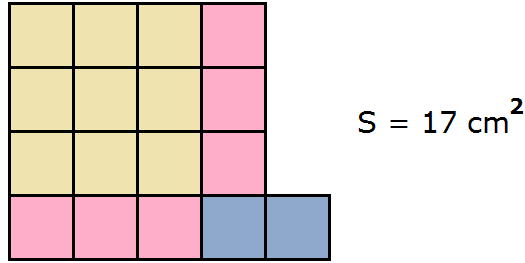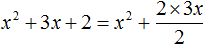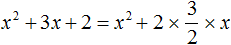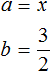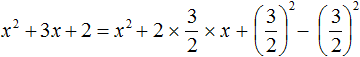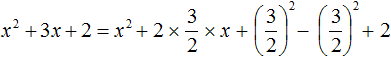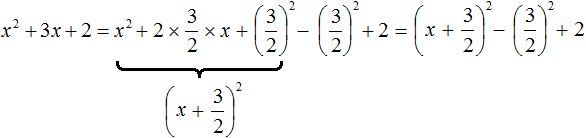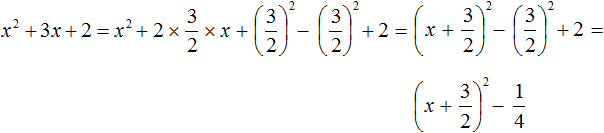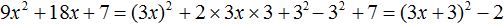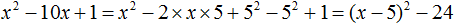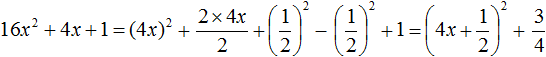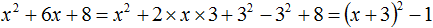//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
- Калькулятор онлайн. Упрощение многочлена. Умножение многочленов.
- Немного теории.
- Произведение одночлена и многочлена. Понятие многочлена
- Преобразование (упрощение) произведения одночлена и многочлена
- Произведение многочленов. Преобразование (упрощение) произведения двух многочленов
- Формулы сокращенного умножения. Квадраты суммы, разности и разность квадратов
- Тема №3. «Многочлены. Преобразование выражений»
- Главная > Документ
- Тождественные преобразования многочленов
- Возведение двучлена в степень
- Возведение трёхчлена в степень
- Выделение полного квадрата из квадратного трёхчлена
- 🎬 Видео
Видео:1 Преобразуйте в многочленСкачать

Калькулятор онлайн.
Упрощение многочлена.
Умножение многочленов.
С помощью данной математической программы вы можете упростить многочлен.
В процессе работы программа:
— умножает многочлены
— суммирует одночлены (приводит подобные)
— раскрывает скобки
— возводит многочлен в степень
Программа упрощения многочленов не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс решения для того чтобы вы могли проконтролировать свои знания по математике и/или алгебре.
Данная программа может быть полезна учащимся общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Видео:Произведение многочленов. 7 класс.Скачать

Немного теории.
Видео:Многочлены. 7 класс.Скачать

Произведение одночлена и многочлена. Понятие многочлена
Среди различных выражений, которые рассматриваются в алгебре, важное место занимают суммы одночленов. Приведем примеры таких выражений:
( 5a^4 — 2a^3 + 0,3a^2 — 4,6a + 8 )
( xy^3 — 5x^2y + 9x^3 — 7y^2 + 6x + 5y — 2 )
Сумму одночленов называют многочленом. Слагаемые в многочлене называют членами многочлена. Одночлены также относят к многочленам, считая одночлен многочленом, состоящим из одного члена.
Например, многочлен
( 8b^5 — 2b cdot 7b^4 + 3b^2 — 8b + 0,25b cdot (-12)b + 16 )
можно упростить.
Представим все слагаемые в виде одночленов стандартного вида:
( 8b^5 — 2b cdot 7b^4 + 3b^2 — 8b + 0,25b cdot (-12)b + 16 = )
( = 8b^5 — 14b^5 + 3b^2 -8b -3b^2 + 16 )
Приведем в полученном многочлене подобные члены:
( 8b^5 -14b^5 +3b^2 -8b -3b^2 + 16 = -6b^5 -8b + 16 )
Получился многочлен, все члены которого являются одночленами стандартного вида, причем среди них нет подобных. Такие многочлены называют многочленами стандартного вида.
За степень многочлена стандартного вида принимают наибольшую из степеней его членов. Так, двучлен ( 12a^2b — 7b ) имеет третью степень, а трехчлен ( 2b^2 -7b + 6 ) — вторую.
Обычно члены многочленов стандартного вида, содержащих одну переменную, располагают в порядке убывания показателей ее степени. Например:
( 5x — 18x^3 + 1 + x^5 = x^5 — 18x^3 + 5x + 1 )
Сумму нескольких многочленов можно преобразовать (упростить) в многочлен стандартного вида.
Иногда члены многочлена нужно разбить на группы, заключая каждую группу в скобки. Поскольку заключение в скобки — это преобразование, обратное раскрытию скобок, то легко сформулировать правила раскрытия скобок:
Если перед скобками ставится знак «+», то члены, заключаемые в скобки, записываются с теми же знаками.
Если перед скобками ставится знак «-», то члены, заключаемые в скобки, записываются с противоположными знаками.
Видео:Деление многочлена на многочлен. 10 класс.Скачать

Преобразование (упрощение) произведения одночлена и многочлена
С помощью распределительного свойства умножения можно преобразовать (упростить) в многочлен произведение одночлена и многочлена. Например:
( 9a^2b(7a^2 — 5ab — 4b^2) = )
( = 9a^2b cdot 7a^2 + 9a^2b cdot (-5ab) + 9a^2b cdot (-4b^2) = )
( = 63a^4b — 45a^3b^2 — 36a^2b^3 )
Произведение одночлена и многочлена тождественно равно сумме произведений этого одночлена и каждого из членов многочлена.
Этот результат обычно формулируют в виде правила.
Чтобы умножить одночлен на многочлен, надо умножить этот одночлен на каждый из членов многочлена.
Мы уже неоднократно использовали это правило для умножения на сумму.
Видео:Схема Горнера. 10 класс.Скачать

Произведение многочленов. Преобразование (упрощение) произведения двух многочленов
Вообще, произведение двух многочленов тождественно равно сумме произведении каждого члена одного многочлена и каждого члена другого.
Обычно пользуются следующим правилом.
Чтобы умножить многочлен на многочлен, надо каждый член одного многочлена умножить на каждый член другого и сложить полученные произведения.
Видео:Алгебра 7 класс (Урок№19 - Многочлены стандартного вида.)Скачать

Формулы сокращенного умножения. Квадраты суммы, разности и разность квадратов
С некоторыми выражениями в алгебраических преобразованиях приходится иметь дело чаще, чем с другими. Пожалуй, наиболее часто встречаются выражения ( (a + b)^2, ; (a — b)^2 ) и ( a^2 — b^2 ), т. е. квадрат суммы, квадрат разности и разность квадратов. Вы заметили, что названия указанных выражений как бы не закончены, так, например, ( (a + b)^2 ) — это, конечно, не просто квадрат суммы, а квадрат суммы а и b. Однако квадрат суммы а и b встречается не так уж часто, как правило, вместо букв а и b в нем оказываются различные, иногда довольно сложные выражения.
Выражения ( (a + b)^2, ; (a — b)^2 ) нетрудно преобразовать (упростить) в многочлены стандартного вида, собственно, вы уже встречались с таким заданием при умножении многочленов:
( (a + b)^2 = (a + b)(a + b) = a^2 + ab + ba + b^2 = )
( = a^2 + 2ab + b^2 )
Полученные тождества полезно запомнить и применять без промежуточных выкладок. Помогают этому краткие словесные формулировки.
( (a + b)^2 = a^2 + b^2 + 2ab ) — квадрат суммы равен сумме квадратов и удвоенного произведения.
( (a — b)^2 = a^2 + b^2 — 2ab ) — квадрат разности равен сумме квадратов без удвоенного произведения.
( a^2 — b^2 = (a — b)(a + b) ) — разность квадратов равна произведению разности на сумму.
Эти три тождества позволяют в преобразованиях заменять свои левые части правыми и обратно — правые части левыми. Самое трудное при этом — увидеть соответствующие выражения и понять, чем в них заменены переменные а и b. Рассмотрим несколько примеров использования формул сокращенного умножения.
Видео:7 класс, 23 урок, Умножение многочлена на многочленСкачать

Тема №3. «Многочлены. Преобразование выражений»
Главная > Документ
| Информация о документе | |
| Дата добавления: | |
| Размер: | |
| Доступные форматы для скачивания: |
Глава 2. Буквенные выражения.
Тема №3. «Многочлены. Преобразование выражений»
Одночленом называют выражение, которое содержит числа, натуральные степени переменных и их произведения. Одночлен называется представленным в стандартном виде , если он записан в виде произведения числового множителя, стоящего на первом месте, и степеней различных переменных.
Числовой множитель у одночлена стандартного вида называется коэффициентом одночлена , сумму показателей степеней переменных называют степенью одночлена.
Многочленом называется алгебраическая сумма одночленов. Если все одночлены в многочлене приведены к стандартному виду и нет подобных слагаемых, то говорят, что это многочлен стандартного вида.
Формулы преобразования многочленов.
Для любых а, b и с верны следующие равенства:
l. a 2 -b 2 = (a — b)(a + b);
2. (а + b) 2 = а 2 + 2аb + b 2 ;
3. (а — b) 2 = а 2 — 2аb + b 2 ;
4. (а + b) 3 = а 3 + 3a 2 b + 3аb 2 + b 3 ;
5. (а — b) 3 = а 3 — 3а 2 b + 3аb 2 — b 3 ;
6. a 3 + b 3 = (а + b)<а 2 -ab + b 2 );
7. a 3 — b 3 = (a — b)<a 2 + ab + b 2 );
8. ах 2 + bx + c = a(x — x 1 )(x — x 2 ), где х 1 и х 2 — корни квадратного уравнения ах 2 +bx + с = 0.
Предлагаю вашему вниманию демонстрационный вариант, изучите на его примере алгоритмы выполнения заданий и попробуйте свои силы.
1. Какое из приведённых ниже выражений тождественно равно произведению
1) -(4 — х)(у — 1) 2) -(х — 4)(1 — у)
3) -(x — 4)(у — 1) 4) (4 — у)(х — 1)
Решение. Рассмотрим каждое из предложенных выражений.
1) -(4 — х)(у — 1) = -(-(x — 4))(-(1 — у)) = -(х — 4)(1 — у) не равно тождественно (х — 4)(1 — у).
2) -(х — 4)(1 — у) не равно тождественно (х — 4)(1 — у).
3) -(х — 4)(у-1) = -(х — 4)(-(1- у)) = (х — 4)(1- у) тождественно равно (х — 4)(1 — у).
4) (4 — у)(х — 1) = 4х — ух + 4х — 4 не равно тождественно (х — 4)(1 — у) = х — ху + 4у — 4.
2. Упростите выражение (3 — 4а) 2 + 8а(3 — 2а).
1)9 2) — 48а — 32а 2 3) 9 — 32а 2 4) 9 — 48а
(3-4а) 2 +8а(3-2а) = 3 2 -2*3*4а+(4а) 2 +3*8а — 2а*8а = 9 — 24а + 16а 2 + 24а — 16а 2 = 9.
3. Найдите числовое значение многочлена 3х 2 — 7ху -1- 4у 2 при х = 2, y = -1.
1) -4 2) 2 3) 30 4) -2
Решение. 3х 2 — 7ху + 4у 2 = (3х 2 — 3ху) — (4ху — 4у 2 ) = = 3х(х — у) — 4у(х — у) = (х — у)(3х — 4у).
Подставляя в полученное выражение значения х = 2, у = —1, получим (2 — (-1))(3 • 2 — 4 •
(-1)) = 3 • (6 + 4) = 3 • 10 = 30.
1) 5у 2 + 3у — 9 2) 5у 2 — 21у — 9 3) -3у 2 + 3у — 9 4) у — 9
Решение. у(у — 9) — (3 — 2у) 2 = у 2 — 9у — (9 — 12у + 4у 2 ) = = у 2 — 9у — 9 + 12у — 4у 2 = -3у 2 + 3у — 9. Ответ: 3.
5. Упростите выражение А- В, если А = (х- 2у)(х + 2y);
В = х 2 — 4ху + 5у 2 .
1) 9у 2 + 4ху 2) 2х 2 — 9у 2 + 4ху 3) -5у 2 4) 4ху — 9у 2 Решение. По формуле сокращённого умножения А = (х — 2у)(х + 2у) = х 2 — 4у 2 .
Следовательно, А — В = х 2 — 4у 2 — (х 2 — 4ху + 5у 2 ) = = х 2 — 4у 2 — х 2 + 4ху — 5у 2 = 4ху — 9у 2 . Ответ: 4.
6. Выполните умножение многочленов: (а + 2)(а 2 — 2а + 4).
1)а 3 + 16 2) а 3 + 8 3) а 3 + 2а 2 + 8 4) а 3 — 8
Решение. По формуле сокращённого умножения а 3 + b 3 = (а + b) (а 2 — аb + b 2 ) заданное выражение (а + 2)(а 2 — 2а + 4) = а 3 + 2 3 = а 3 + 8.
7. Разложите многочлен 5х 2 — 5у 2 — ax + ay на линейные множители.
1) (5 — а)(х — у) 2)(x 2 — у 2 )(5 — а)
3) (х + у)(5x — 5у — а) 4) (x — у)(5х + 5y — а)
Решение. 5х 2 — 5у 2 — ах + ау = 5(х 2 — у 2 ) — а(х — у) = 5(х-у)(х+у)-а(х-у) = (х-у)(5(х+у)-а) = (x-у)(5х+5у-а).
8. Соотнесите каждое выражение
A> 


Решение. Преобразуем каждое из заданных выражений.
A) 
Б) 
B) 
Видео:АЛГЕБРА 7 класс. Преобразование целого выражения в многочлен | ВидеоурокСкачать

Тождественные преобразования многочленов
Видео:Преобразование целых выражений в многочлен. 7 клСкачать

Возведение двучлена в степень
Двучлен — это многочлен, состоящий из двух членов. В прошлых уроках мы возводили двучлен во вторую и третью степень, тем самым получили формулы сокращенного умножения:
Но двучлен можно возводить не только во вторую и третью степень, но и в четвёртую, пятую или более высокую степень.
К примеру, возведём двучлен a + b в четвертую степень:
Представим это выражение в виде произведения двучлена a + b и куба этого же двучлена
Сомножитель (a + b) 3 можно заменить на правую часть формулы куба суммы двух выражений. Тогда получим:
А это обычное перемножение многочленов. Выполним его:
То есть при возведении двучлена a + b в четвертую степень получается многочлен a 4 + 4a 3 b + 6a 2 b 2 + 4ab 3 + b 4
Возведение двучлена a + b в четвертую степень можно выполнить ещё и так: представить выражение (a + b) 4 в виде произведения степеней (a + b) 2 (a + b) 2
Но выражение (a + b) 2 равно a 2 + 2ab + b 2 . Заменим в выражении (a + b) 2 (a + b) 2 квадраты суммы на многочлен a 2 + 2ab + b 2
А это опять же обычное перемножение многочленов. Выполним его. У нас получится тот же результат, что и раньше:
Видео:Преобразование целого выражения в многочлен. Алгебра, 7 классСкачать

Возведение трёхчлена в степень
Трёхчлен — это многочлен, состоящий из трёх членов. Например, выражение a + b + c является трёхчленом.
Иногда может возникнуть задача возвести трёхчлен в степень. Например, возведём в квадрат трехчлен a + b + c
Два члена внутри скобок можно заключить в скобки. К примеру, заключим сумму a + b в скобки:
В этом случае сумма a + b будет рассматриваться как один член. Тогда получается, что в квадрат мы возводим не трёхчлен, а двучлен. Сумма a + b будет первым членом, а член c — вторым членом. А как возводить в квадрат двучлен мы уже знаем. Для этого можно воспользоваться формулой квадрата суммы двух выражений:
Применим эту формулу к нашему примеру:
Таким же способом можно возвести в квадрат многочлен, состоящий из четырёх и более членов. Например, возведем в квадрат многочлен a + b + c + d
Представим многочлен в виде суммы двух выражений: a + b и c + d . Для этого заключим их в скобки:
Теперь воспользуемся формулой квадрата суммы двух выражений:
Видео:Преобразование целых выражений. 7 класс.Скачать

Выделение полного квадрата из квадратного трёхчлена
Ещё одно тождественное преобразование, которое может пригодиться при решении задач это выделение полного квадрата из квадратного трёхчлена.
Квадратным трехчленом называют трёхчлен второй степени. Например, следующие трехчлены являются квадратными:
Идея выделения полного квадрата из таких трехчленов заключается в том, чтобы представить исходный квадратный трехчлен в виде выражения (a + b) 2 + c , где (a + b) 2 полный квадрат, а c — некоторое числовое или буквенное выражение.
Например, выделим полный квадрат из трёхчлена 4x 2 + 16x + 19 .
Для начала нужно построить выражение вида a 2 + 2ab + b 2 . Строить мы его будем из трехчлена 4x 2 + 16x + 19 . Для начала определимся какие члены будут играть роли переменных a и b
Роль переменной a будет играть член 2x , поскольку первый член трехчлена 4x 2 + 16x + 19 , а именно 4x 2 получается если 2x возвести в квадрат:
Итак, переменная a равна 2x
Теперь возвращаемся к исходному трёхчлену и сразу обращаем внимание на выражение 16x . Это выражение является удвоенным произведением первого выражения a (в нашем случае это 2x ) и второго пока неизвестного нам выражения b . Временно поставим на его место вопросительный знак:
Если внимательно посмотреть на выражение 2 × 2x × ? = 16x , то интуитивно станет понятно, что членом b в данной ситуации является число 4, поскольку выражение 2 × 2x равно 4x , и чтобы получить 16x нужно домножить 4x на 4 .
Отсюда делаем вывод, что переменная b равна 4
Значит, нашим полным квадратом будет выражение (2x) 2 + 2 × 2x × 4 + 4 2
Теперь у нас всё готово для выделения полного квадрата из трёхчлена 4x 2 + 16x + 19 .
Итак, возвратимся к исходному трехчлену 4x 2 + 16x + 19 и попробуем аккуратно внедрить в него полученный нами полный квадрат (2x) 2 + 2 × 2x × 4 + 4 2
Вместо 4x 2 записываем (2x) 2
Далее вместо 16x записываем удвоенное произведение, а именно 2 × 2x × 4
Далее прибавляем квадрат второго выражения:
А член 19 пока переписываем как есть:
4x 2 + 16x + 19 = (2x) 2 + 2 × 2x × 4 + 4 2 + 19
Теперь обратим внимание на то, что полученный нами многочлен (2x) 2 + 2 × 2x × 4 + 4 2 + 19 не тождественен изначальному трёхчлену 4x 2 + 16x + 19 . Убедиться в этом можно приведя многочлен (2x) 2 + 2 × 2x × 4 + 4 2 + 19 к стандартному виду:
(2x) 2 + 2 × 2x × 4 + 4 2 + 19 = 4x 2 + 16x + 4 2 + 19
Видим, что получается многочлен 4x 2 + 16x + 4 2 + 19 , а должен был получиться 4x 2 + 16x + 19 . Это по причине того, что член 4 2 был искусственно внедрён в изначальный трёхчлен с целью организовать полный квадрата из трёхчлена 4x 2 + 16x + 19 .
Чтобы сохранить значение исходного многочлена, нужно после прибавления члена 4 2 сразу же вычесть его
4x 2 + 16x + 19 = (2x) 2 + 2 × 2x × 4 + 4 2 − 4 2 + 19
Теперь выражение (2x) 2 + 2 × 2x × 4 + 4 2 можно свернуть, то есть записать в виде (a + b) 2 . В нашем случае получится выражение (2x + 4) 2
4x 2 + 16x + 19 = (2x) 2 + 2 × 2x × 4 + 4 2 − 4 2 + 19 = (2x + 4) 2 − 4 2 + 19
Оставшиеся члены −4 2 и 19 можно сложить. −4 2 это −16 , отсюда −16 + 19 = 3
4x 2 + 16x + 19 = (2x) 2 + 2 × 2x × 4 + 4 2 − 4 2 + 19 = (2x + 4) 2 − 4 2 + 19 = (2x + 4) 2 + 3
Значит, 4x 2 + 16x + 19 = (2x + 4) 2 + 3
Пример 2. Выделить полный квадрат из квадратного трёхчлена x 2 + 2x + 2
Сначала построим выражение вида a 2 + 2 ab + b 2 . Роль переменной a в данном случае играет x, поскольку x 2 = x 2 .
Следующий член исходного трёхчлена 2x перепишем в виде удвоенного произведение первого выражения (это у нас x ) и второго выражения b (это будет 1).
Если b = 1 , то полным квадратом будет выражение x 2 + 2x + 1 2 .
Теперь вернёмся к исходному квадратному трёхчлену и внедрим в него полный квадрата x 2 + 2x + 1 2
x 2 + 2x + 2 = x 2 + 2x + 1 2 − 1 2 + 2 = (x + 1) 2 + 1
Как и в прошлом примере член b (в данном примере это 1) после прибавления сразу был вычтен с целью сохранения значения исходного трёхчлена.
Рассмотрим следующее числовое выражение:
Значение этого выражения равно 17
Попробуем выделить в этом числовом выражении полный квадрат. Для этого сначала построим выражение вида a 2 + 2ab + b 2 . Роль переменной a в данном случае играет число 3 , поскольку первый член выражения 9 + 6 + 2 , а именно 9 можно представить как 3 2 .
Второй член 6 представим в виде удвоенного произведения первого члена 3 и второго 1
То есть переменная b будет равна единице. Тогда полным квадратом будет выражение 3 2 + 2 × 3 × 1 + 1 2 . Внедрим его в исходное выражение:
3 2 + 6 + 2 = 3 2 + 2 × 3 × 1 + 1 2 − 1 2 + 2
Свернем полный квадрат, а члены −1 2 и 2 слóжим:
3 2 + 6 + 2 = 3 2 + 2 × 3 × 1 + 1 2 − 1 2 + 2 = (3 + 1) 2 + 1
Получилось выражение (3 + 1) 2 + 1 , которое по прежнему равно 17
(3 + 1) 2 +1 = 4 2 + 1 = 17
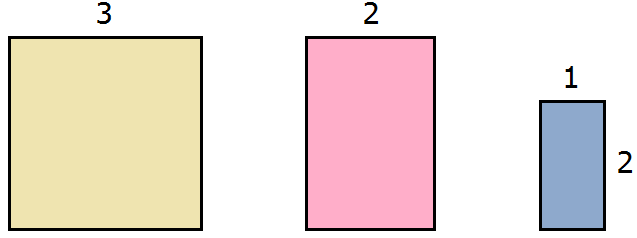
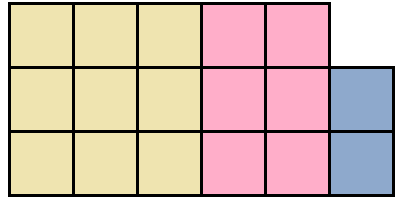
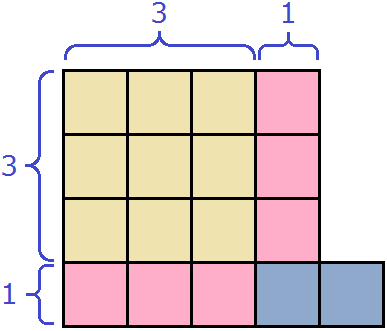
Допустим, у нас имеются квадрат и два прямоугольника. Квадрат со стороной 3 см, прямоугольник со сторонами 2 см и 3 см, а также прямоугольник со сторонами 1 см и 2 см
Вычислим площадь каждой фигуры. Площадь квадрата будет составлять 3 2 = 9 см 2 , площадь розового прямоугольника — 2 × 3 = 6 см 2 , площадь сиреневого — 1 × 2 = 2 см 2
Запишем сумму площадей этих прямоугольников:
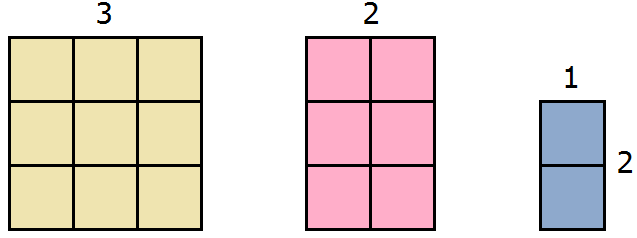
Это выражение можно понимать как объединение квадрата и двух прямоугольников в единую фигуру:
Тогда получается фигура, площадь которой 17 см 2 . Действительно, в представленной фигуре содержится 17 квадратов со стороной 1 см.
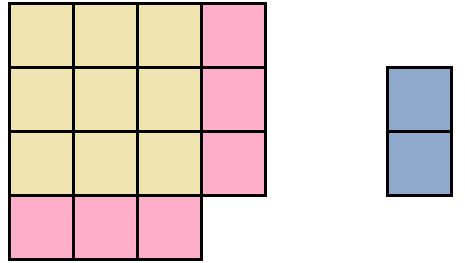
Попробуем из имеющейся фигуры образовать квадрат. Причем максимально большой квадрат. Для этого будем использовать части от розового и сиреневого прямоугольника.
Чтобы образовать максимально большой квадрат из имеющейся фигуры, можно желтый квадрат оставить без изменений, а половину от розового прямоугольника прикрепить к нижней части желтого квадрата:
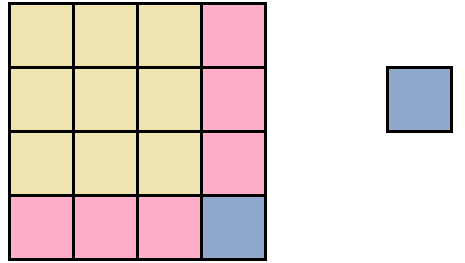
Видим, что до образования полного квадрата не хватает еще одного квадратного сантиметра. Его мы можем взять от сиреневого прямоугольника. Итак, возьмем один квадрат от сиреневого прямоугольника и прикрепим его к образуемому большому квадрату:
Теперь внимательно посмотрим к чему мы пришли. А именно на желтую часть фигуры и розовую часть, которая по сути увеличила прежний жёлтый квадрат. Не означает ли это то, что была сторона квадрата равная 3 см, и эта сторона была увеличена на 1 см, что привело в итоге к увеличению площади?
(3 + 1) 2
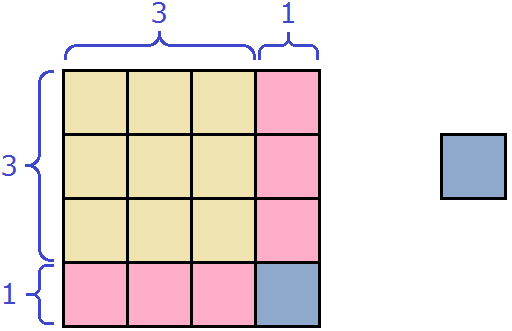
Выражение (3 + 1) 2 равно 16 , поскольку 3 + 1 = 4 , а 4 2 = 16 . Этот же результат можно получить, если воспользоваться формулой квадрата суммы двух выражений:
(3 + 1) 2 = 3 2 + 6 + 1 = 9 + 6 + 1 = 16
Действительно, в образовавшемся квадрате содержится 16 квадратов.
Оставшийся один квадратик от сиреневого прямоугольника можно прикрепить к образовавшемуся большому квадрату. Ведь речь изначально шла о единой фигуре:
(3 + 1) 2 + 1
Прикрепление маленького квадратика к имеющемуся большому квадрату описывается выражением (3 + 1) 2 + 1 . А это есть выделение полного квадрата из выражения 9 + 6 + 2
9 + 6 + 2 = 3 2 + 6 + 2 = 3 2 + 2 × 3 × 1 + 1 2 − 1 2 + 2 = (3 + 1) 2 + 1
Выражение (3 + 1) 2 + 1 , как и выражение 9 + 6 + 2 равно 17 . Действительно, площадь образовавшейся фигуры равна 17 см 2 .
Пример 4. Выполним выделение полного квадрата из квадратного трёхчлена x 2 + 6x + 8
x 2 + 6x + 8 = x 2 + 2 × x × 3 + 3 2 − 3 2 + 8 = (x + 3) 2 − 1
В некоторых примерах при построении выражения a 2 + 2ab + b 2 не бывает возможным сразу определить значения переменных a и b .
Например, выполним выделение полного квадрата из квадратного трёхчлена x 2 + 3x + 2
Переменной a соответствует x . Второй член 3x нельзя представить в виде удвоенного произведения первого выражения и второго. В этом случае второй член следует умножить на 2, и чтобы значение исходного многочлена не изменилось, сразу же выполнить деление на 2. Выглядеть это будет так:
Получившаяся дробь 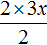

Теперь второй член представлен в виде удвоенного произведения первого выражения и второго. Переменная a , как было сказано ранее, равна x . А переменная b равна дроби
Возвращаемся к нашему примеру и прибавляем квадрат второго выражения, и чтобы значение выражения не изменилось, сразу же вычитаем его:
Прибавляем оставшийся член 2
Свернём полный квадрат:
Оставшийся квадрат второго выражения и число 2 можно сложить. В итоге получим:
Пример 6. Выполним выделение полного квадрата из квадратного трёхчлена 9x 2 + 18x + 7
Пример 7. Выполним выделение полного квадрата из квадратного трёхчлена x 2 − 10x + 1
В данном трёхчлене первые два члена связаны знаком «минус». В этом случае как и раньше нужно выделить полный квадрат, но это будет квадрат разности. Проще говоря, нужно построить выражение вида a 2 − 2ab + b 2 .
Пример 8. Выполним выделение полного квадрата из квадратного трёхчлена 16x 2 + 4x + 1
Пример 9. Разложить многочлен x 2 + 6x + 8 на множители при помощи выделения полного квадрата.
Сначала выделим полный квадрат:
Получившийся многочлена (x + 3) 2 − 1 является разностью квадратов, поскольку единица может быть представлена в виде 1 2 . Воспользуемся формулой разности квадратов и разложим многочлен (x + 3) 2 − 1 на множители:
🎬 Видео
Многочлен и его стандартный вид. Алгебра, 7 классСкачать

Произведение одночлена и многочлена. Умножение одночлена и многочлена. 7 класс.Скачать
Деление многочленов | Математика | TutorOnlineСкачать

РЕШЕНИЕ УРАВНЕНИЯ С МНОГОЧЛЕНАМИ. Примеры | АЛГЕБРА 7 классСкачать

7 класс - Алгебра - Преобразование целого выражения в многочленСкачать

Произведение многочленов. Разложение многочлена на множители способом группировки. 7 класс.Скачать

Сложение и вычитание многочленов. Алгебра, 7 классСкачать

Математика| Разложение квадратного трехчлена на множители.Скачать

ЧТО НАДО ГОВОРИТЬ ЕСЛИ НЕ СДЕЛАЛ ДОМАШКУ!Скачать