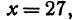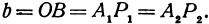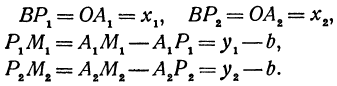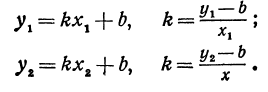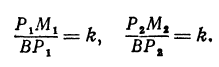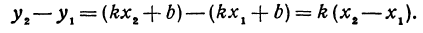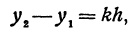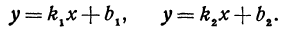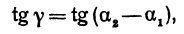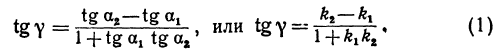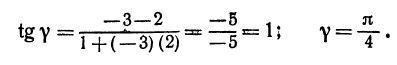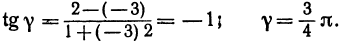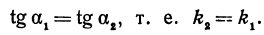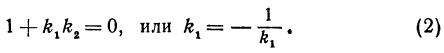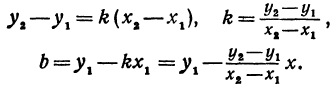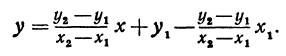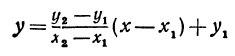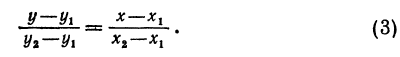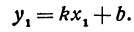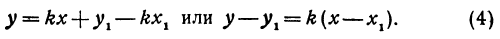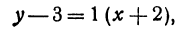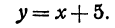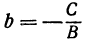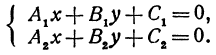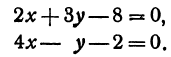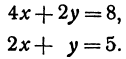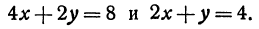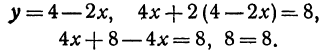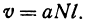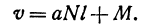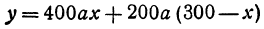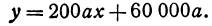Преобразуйте линейное уравнение с двумя переменными x и y к виду линейной функции y = kx + m и выпишите коэффициенты k и m:
а) 12 x − y = − 17 ;
б ) y − 19 x = 5 ;
в ) y − 36 x = − 40 ;
г) 15 x + y = 53 .
- ГДЗ учебник по алгебре 7 класс Мордкович. §8. Линейная функция и ее график. Номер №8.8.
- Решение а
- Решение б
- Решение в
- Решение г
- Как преобразовать уравнение с двумя переменными в линейную функцию
- Линейная функция — определение и вычисление с примерами решения
- Основное свойство линейной функции
- Задачи на прямую
- Общее уравнение прямой. Неявная линейная функция
- Система двух уравнений первой степени
- Примеры применения линейной функции
- 🔍 Видео
Видео:Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать

ГДЗ учебник по алгебре 7 класс Мордкович. §8. Линейная функция и ее график. Номер №8.8.
Решение а
12 x − y = − 17
y = 12 x + 17
k = 12
m = − 17
Решение б
y − 19 x = 5
y = 19 x + 5
k = 19
m = 5
Решение в
y − 36 x = − 40
y = 36 x − 40
k = 36
m = − 40
Решение г
15 x + y = 53
y = − 15 x + 53
k = − 15
m = 53
Видео:ГРАФИК ЛИНЕЙНОГО УРАВНЕНИЯ С ДВУМЯ ПЕРЕМЕННЫМИ 7 КЛАСС видеоурокСкачать

Как преобразовать уравнение с двумя переменными в линейную функцию
В первом задании мы рассмотрели линейные уравнения с одной переменной. Например, уравнения `2x+5=0`, `3x+(8x-1)+9=0` являются линейными уравнениями с переменной `x`. Уравнение, содержащее переменные `x` и `y`, называется уравнением с двумя переменными. Например, уравнения `2x-3=5`, `x^2+xy-y^2=7` являются уравнениями с двумя переменными.
Уравнение вида `ax+by=c` называется линейным уравнением с двумя переменными, где `x` и `y` переменные, `a`, `b`, `c` — некоторые числа.
Например, уравнения `2x+y=3`, `x-y=0` являются линейными уравнениями с двумя переменными.
Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное равенство.
Например, `x=3`, `y=4` является решением уравнения `2x+3y=18`, будем эту пару чисел записывать так `(3;4)`. Очевидно, что пара чисел `(4;3)` не является решением уравнения, т. к. `2*4+3*3=17!=18`. При нахождении решений с двумя переменными на первом месте в паре чисел пишем значение для переменной `x`, а на втором месте – значение переменной `y`.
Если каждое решение одного уравнения является решением второго уравнения и обратно, то данные уравнения называются равносильными. Например, решения уравнений `2x+y=3` и `4x+2y=6` совпадают, следовательно, эти уравнения равносильные.
1) если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному;
2) если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получим уравнение, равносильное данному.
Укажите три различных решения для уравнения `3x+y-2=0`.
Если `x=0`, то `y=2`; если `y=0`, то `x=2/3`; если `x=1`, то `y=-1`.
Таким образом, пары чисел `(0;2)`, `(2/3;0)`, `(1;-1)` являются решениями данного уравнения. Заметим, что данное уравнение имеет бесконечно много решений. Для заданного значения `x` значение `y=2-3x`, т. е. любая пара чисел `(x;2-3x)`, где `x` — любое число, является решением уравнения.
Рассмотрим координатную плоскость `Oxy` и отметим на ней все точки `(x,y)`, для которых пара чисел `x` и `y` является решениями уравнения. Например, рассмотрим уравнение `y=2`. Этому уравнению удовлетворяют все пары чисел `(x;2)`.Точки, для которых `x` — любое число, а `y=2`, лежат на прямой `y=2`. Эта прямая параллельна оси `x` и проходит через точку `(0;2)` (см. рис. 1).
Рассмотрим уравнение `x=3`. Каждая пара чисел, являющаяся решением данного уравнения, изображается точкой с координатами `x` и `y` на координатной плоскости `Oxy`. Решениями данного уравнения являются пары чисел `(3;y)`. Точки с координатами `x=3` и `y` лежат на прямой `x=3`, эта прямая параллельна оси `Oy` и проходит через точку `(3;0)` (см. рис. 2).
Графиком уравнения с двумя переменными называется множество всех точек координатной плоскости, координаты которых являются решениями данного уравнения.
На рис. 1 графиком уравнения является прямая `y=2`, на рис. 2 графиком уравнения является прямая `x=3`.
Рассмотрим теперь уравнение `2x+3y-1=0`. Выразим переменную `y` через `x`, получаем `y=1/3-2/3x`, это уравнение задаёт линейную функцию, и нам известно, что её графиком является прямая. Чтобы построить эту прямую, достаточно рассмотреть две точки, координаты которых удовлетворяют уравнению, а затем через эти две точки провести прямую. При `x=0` `y=1/3` и при `x=1/2` `y=0`. График данного уравнения приведён на рис. 3.
Рассмотрим уравнение `(x-4)(x+y-4)=0`. Произведение двух скобок равно нулю, каждая скобка может равняться нулю. Наше уравнение распадётся на два уравнения: `x=4` и `x+y-4=0`. Графиком первого уравнения является прямая, параллельная оси `Oy` и проходящая через точку `(4;0)`. Графиком второго уравнения является график линейной функции `y=4-x`, эта прямая проходит через точки `(4;0)` и `(0;4)`. График данного уравнения приведён на рис. 4.
Постройте график уравнения `|x|+|y|=1`.
Этот пример можно решать двумя способами. Пусть `x>=0` и `y>=0`, точки с такими координатами лежат в первой четверти. Получаем уравнение `x+y=1`, так как `|x|=x` и `|y|=y`. Графиком данного уравнения является прямая, проходящая через точки `A(1;0)` и `B(0;1)`. Графику исходного уравнения принадлежат точки полученной прямой, лежащие в первой четверти, т. е. графику принадлежат точки отрезка `AB`, где `A(1;0)` и `B(0;1)`.
Пусть теперь `x =0` тогда получаем уравнение `-x+y=1`, рассматриваем точки полученной прямой, лежащие во второй четверти. Это будет отрезок `BC`, где `C(-1;0)`. При `x =0`, `y =0`, тогда наше уравнение эквивалентно уравнению `y=1-|x|`. В первом задании мы строили график функции `y=|x|` (см. рис. 6). График функции `y=-|x|` получается зеркальным отражением относительно оси `Ox` графика функции `y=|x|` (см. рис. 7). График функции `y=1-|x|` получается из графика функции `y=-|x|` сдвигом вдоль оси `Oy` на единицу вверх (см. рис. 8). У полученного графика рассматриваем только точки, для которых `y>=0`. Получим ломаную `ABC` с рис. 5.
Видео:Линейное уравнение с двумя переменными. 7 класс.Скачать

Линейная функция — определение и вычисление с примерами решения
Содержание:
Рассмотрим уравнение с двумя неизвестными
где 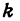
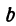
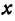
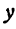
удовлетворяют следующие пары:
Для того чтобы найти пару чисел, удовлетворяющих уравнению 

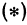

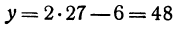
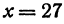
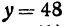
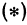


Так как в данном уравнении 

Для 


Функцию 
Пример:
Вычислить значения линейной функции, определяемой уравнением 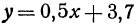
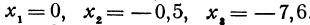
Решение:
Если 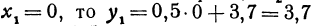
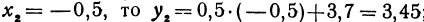
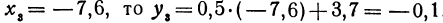
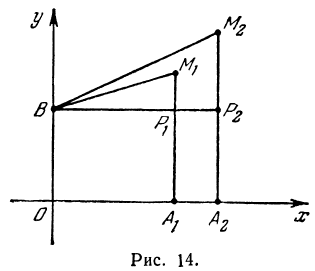
Покажем, что если принять пару чисел 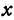
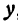
В самом деле, рассмотрим точку 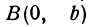
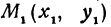
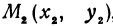
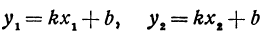
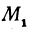
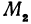
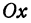
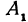
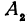
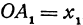

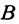
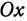
Предположим, что точки 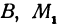
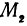
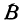
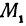
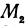
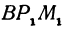
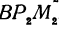
Но так как 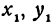
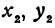
Выражения 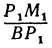
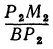
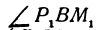
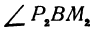
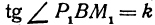
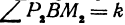

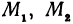
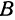
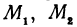
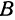
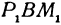
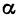
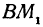
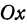
Так как 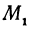
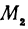
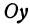
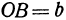
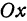
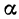
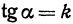
Число 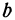
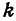
Предыдущие рассуждения позволяют сделать вывод: линейная функция 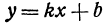
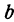
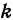
Например, линейная функция 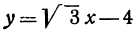
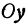
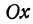
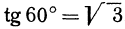
Если имеем определенную прямую, отсекающую на оси 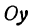
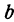
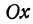
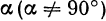
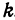
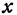
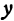
Очевидно, имеет место и такое предложение: Всякой прямой, отсекающей на оси 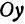
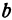
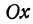
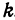
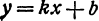
Координаты любой, точки, лежащей на указанной прямой, удовлетворяют уравнению (1), поэтому уравнение 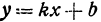
Таким образом, всякая линейная функция является уравнением некоторой прямой.
Отметим частные случаи.
1. Пусть 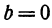
Прямая, определяемая этим уравнением, проходит через начало координат. Здесь 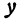
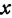
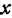
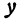
2. Пусть 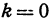
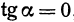
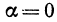
Этому уравнению соответствует прямая, параллельная оси 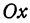
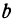
На основании всего сказанного в этом параграфе легко решаются следующие задачи.
Пример:
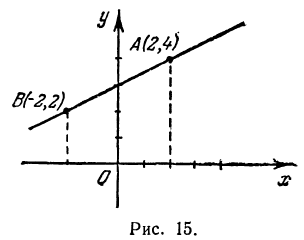
Даны точки 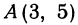
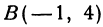
Решение:
Если точка лежит на прямой, то ее координаты должны удовлетворять уравнению прямой. Поэтому для решения задачи подставим координаты точки 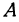
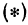
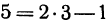
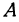
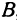
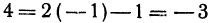
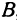
Пример:
Построить прямую, уравнение которой
Решение:
Чтобы построить прямую, надо знать, например, две ее точки. Поэтому дадим 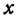
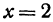
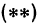
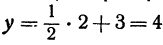
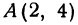
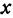
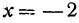
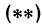
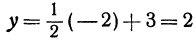
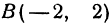
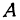
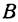
Видео:Алгебра 7 Линейное уравнение с двумя переменными и его графикСкачать

Основное свойство линейной функции
Рассмотрим линейную функцию 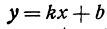
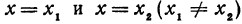
Здесь первое и второе значения 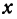
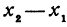

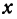
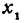
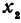
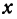
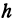
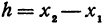
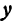
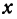
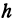
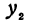
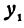
т. е. приращение линейной функции пропорционально приращению независимого переменного.
Это и есть основное свойство линейной функции.
Заметим, что 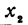
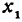
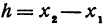
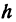
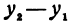
Пример:
Найдем приращение функции 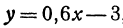
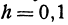
Решение:
По основному свойству 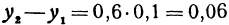
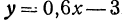
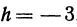
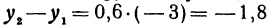
Пример:
Найдем приращение функции 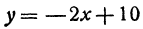
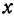

Задачи на прямую
Пример:
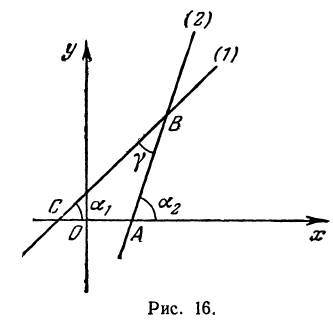
Найти угол 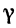
Решение:
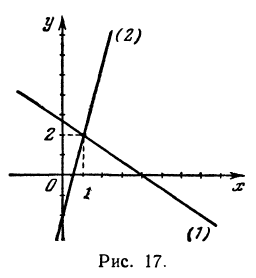
При пересечении прямых образуются четыре попарно равных угла. Найдя один из них, легко найти и другие. На рис. 16 прямые обозначены соответственно (1) и (2).
Угол 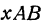
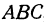
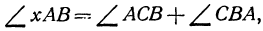
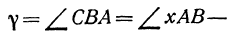
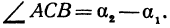
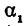
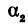
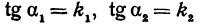
Пример:
Найти угол между прямыми, заданными уравнениями 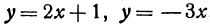
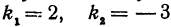
Решение:
Применяя формулу (1), получим:
Если же будем считать, что 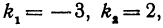
Получены два ответа: сначала найден острый угол между заданными прямыми, а затем — тупой.
Если заданы две параллельные прямые, то углы 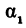
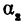
Таким образом, мы приходим к выводу: если прямые параллельны, то их угловые коэффициенты равны.
Если прямые перпендикулярны, то угол между ними равен 90°, т. е. 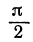
Это и есть условие перпендикулярности двух прямых. Это условие удобно запомнить в следующей формулировке: если две прямые перпендикулярны, то их угловые коэффициенты обратны по величине и противоположны по знаку.
Пример:
Найдем угол между прямыми, заданными уравнениями 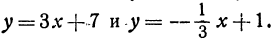
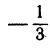
Решение:
Следовательно, рассматриваемые прямые перпендикулярны.
Пример:
Даны две точки: 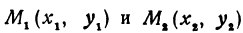
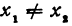
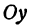
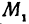
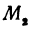
Решение:
Искомая прямая не параллельна оси 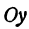
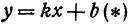
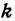
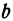
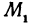
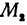
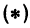
В уравнениях 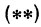
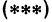
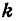
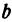
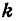
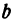
Решая систему, находим:
Подставляя найденные выражения в уравнение 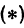
Это и есть уравнение прямой, проходящей через две точки, не расположенные на прямой, параллельной оси 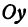
Пример:
Написать уравнение прямой, проходящей через данную точку 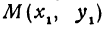
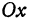
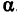
Решение:
Прежде всего найдем угловой коэффициент искомой прямой: он равен тангенсу угла 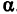
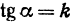
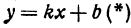
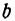
Так как прямая должна проходить через точку 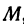
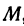
Находим отсюда неизвестное 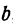
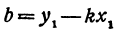
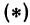
Это и есть уравнение прямой, проходящей через точку 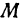
Если в уравнении (4) менять направление, не меняя точку 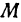
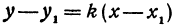
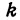
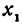
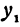
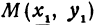
Пример:
Напишем уравнение прямой, проходящей через точку 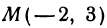
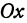
Решение:
Так как 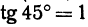
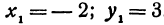
Общее уравнение прямой. Неявная линейная функция
Рассмотрим уравнение первой степени с двумя неизвестными
Решим его относительно 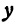
т. е. мы получили линейную функцию, где 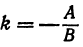
Уравнения (1) и (2) равносильны, поэтому пара чисел 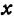
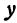
Координаты любой точки, лежащей на этой прямой, удовлетворяют уравнению (1), поэтому будем называть его также уравнением прямой. Рассмотрим особо случай, когда 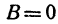
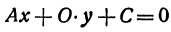
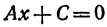
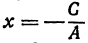
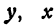
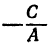
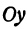
Из уравнения (1) (если 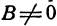
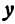
Система двух уравнений первой степени
Напомним, что две прямые, расположенные на плоскости, могут или пересекаться, или быть параллельными (т. е. не пересекаться), или сливаться (в этом случае можно сказать, что они пересекаются в каждой своей точке). Рассмотрим систему двух уравнений
Каждое из этих уравнений является уравнением прямой. Решить систему — это значит найти значения 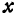
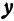
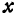
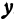
Пример:
Найдем точку пересечения двух прямых:
Решение:
Решая эту систему, получим: 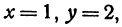
Пример:
Найдем точку пересечения двух прямых:
Решение:
Решая эту систему, получим: 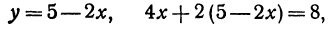
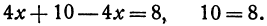
Пример:
Найдем точку пересечения данных прямых
Решение:
Решая эту систему, получим:
Полученное равенство всегда справедливо, т. е. справедливо при любом значении 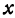
Заметим, что два уравнения, рассматриваемые в этом примере, являются равносильными, поэтому они и представляют одну и ту же прямую.
Примеры применения линейной функции
Линейная функция встречается в формулировках многих физических законов и технических задач. Приведем примеры.
Пример:
Если точка движется равномерно по прямой, то ее расстояние от выбранной точки (от начала координат) выражается при помощи уравнения 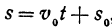
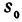
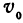
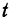
Пример:
Закон Ома записывается в виде 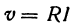
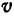
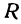
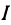
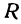
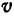
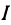
Пример:
Если стоимость провоза единицы товара по железной дороге равна 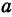
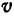
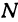
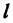
Если же стоимость товара на месте равна 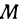
Здесь 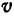
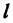
Линейная функция встречается в различных областях, но, где бы она ни встречалась, ее всегда можно рассматривать как уравнение прямой. Этим обстоятельством часто пользуются при решении задач.
Пример:
Два города А и В, расстояние между которыми равно 300 км, находятся на одной железнодорожной магистрали. На этой же магистрали между городами А к В надо выбрать пункт С, в котором предполагается устроить склад нефти для снабжения указанных городов. Надо выбрать пункт С так, чтобы общая стоимость перевозок нефти для снабжения города А и города В была наименьшей. Известно, что город А потребляет 400 т нефти, а город В —200 т. Перевозка одной тонны нефти на один километр обходится в 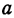
Решение:
Обозначим расстояние от А до предполагаемого пункта С через 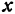
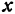
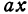
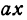
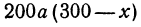
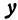
Это линейная функция. Если примем 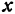
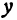
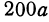
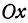
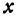
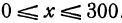
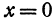
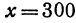
Так как пункт С надо выбрать так, чтобы стоимость была наименьшей, то его следует расположить в городе А; если же этого сделать нельзя по каким-либо соображениям, то, чем ближе расположить его к А, тем выгодней.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Квадратичная функция
- Тригонометрические функции
- Производные тригонометрических функции
- Производная сложной функции
- Функции нескольких переменных
- Комплексные числ
- Координаты на прямой
- Координаты на плоскости
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
🔍 Видео
Решение системы линейных уравнений графическим методом. 7 класс.Скачать

7 класс, 8 урок, Линейное уравнение с двумя переменными и его графикСкачать

ЛИНЕЙНОЕ УРАНЕНИЕ С ДВУМЯ ПЕРЕМЕННЫМИ — Как решать линейное уравнение // Алгебра 7 классСкачать

Уравнение с двумя переменными и его график. Алгебра, 9 классСкачать

График линейного уравнения с двумя переменными. 6 класс.Скачать

Линейная функция и ее график. 7 класс.Скачать

Линейная Функция — как БЫСТРО построить график и получить 5-куСкачать

Линейное уравнение с двумя переменными и его график. График линейной функции - 7 класс алгебраСкачать

Линейное уравнение с двумя переменными и его график | Алгебра 7 класс #43 | ИнфоурокСкачать

График линейного уравнения с двумя переменными, 7 классСкачать

Линейные уравнения с двумя переменными. Построение графиковСкачать

Видеоурок ЛИНЕЙНОЕ УРАВНЕНИЕ С ДВУМЯ ПЕРЕМЕННЫМИ 7 КЛАСССкачать

Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Нелинейные уравнения с двумя переменными и их геометрический смысл. 9 класс.Скачать

МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать