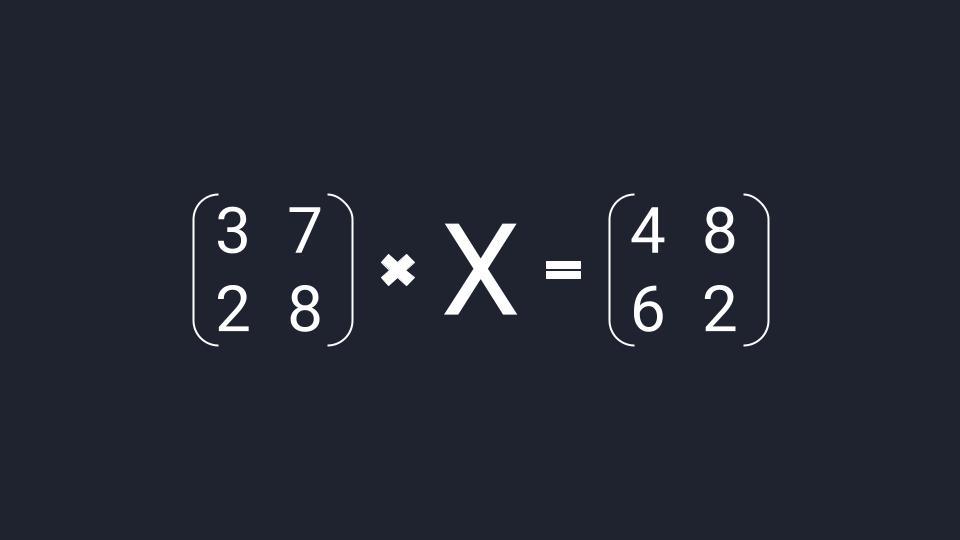Финальная глава саги.
Линейная алгебра и, в частности, матрицы — это основа математики нейросетей. Когда говорят «машинное обучение», на самом деле говорят «перемножение матриц», «решение матричных уравнений» и «поиск коэффициентов в матричных уравнениях».
Понятно, что между простой матрицей в линейной алгебре и нейросетью, которая генерирует котов, много слоёв усложнений, дополнительной логики, обучения и т. д. Но здесь мы говорим именно о фундаменте. Цель — чтобы стало понятно, из чего оно сделано.
Краткое содержание прошлых частей:
- Линейная алгебра изучает векторы, матрицы и другие понятия, которые относятся к упорядоченным наборам данных. Линейной алгебре интересно, как можно трансформировать эти упорядоченные данные, складывать и умножать, всячески обсчитывать и находить в них закономерности.
- Вектор — это набор упорядоченных данных в одном измерении. Можно упрощённо сказать, что это последовательность чисел.
- Матрица — это тоже набор упорядоченных данных, только уже не в одном измерении, а в двух (или даже больше).
- Матрицу можно представить как упорядоченную сумку с данными. И с этой сумкой как с единым целым можно совершать какие-то действия. Например, делить, умножать, менять знаки.
- Матрицы можно складывать и умножать на другие матрицы. Это как взять две сумки с данными и получить третью сумку, тоже с данными, только теперь какими-то новыми.
- Матрицы перемножаются по довольно замороченному алгоритму. Арифметика простая, а порядок перемножения довольно запутанный.
И вот наконец мы здесь: если мы можем перемножать матрицы, то мы можем и решить матричное уравнение.
❌ Никакого практического применения следующего материала в народном хозяйстве вы не увидите. Это чистая алгебра в несколько упрощённом виде. Отсюда до практики далёкий путь, поэтому, если нужно что-то практическое, — посмотрите, как мы генерим Чехова на цепях Маркова.
- Что такое матричное уравнение
- Шаг 1. Упрощаем уравнение
- Шаг 2. Вводим единичную матрицу
- Шаг 3. Находим обратную матрицу
- Шаг 4. Вычисляем неизвестную матрицу
- Шаг 5. Проверяем уравнение
- Ну и что
- Сведение системы линейных уравнений к матрице.
- Пример записи системы линейных уравнений с помощью матричного уравнения
- Метод элементарных преобразований (методы Гаусса и Гаусса-Жордана для нахождения обратных матриц).
- Метод Гаусса
- Прямой ход метода Гаусса
- Обратный ход метода Гаусса
- Метод Гаусса-Жордана
- Метод Гаусса
- Прямой ход метода Гаусса
- Обратный ход метода Гаусса
- Метод Гаусса-Жордана
- Метод Гаусса
- Метод Гаусса-Жордана
Видео:Математика без Ху!ни. Метод Гаусса.Скачать

Что такое матричное уравнение
Матричное уравнение — это когда мы умножаем известную матрицу на матрицу Х и получаем новую матрицу. Наша задача — найти неизвестную матрицу Х.
Видео:Матричный метод решения систем уравненийСкачать

Шаг 1. Упрощаем уравнение
Вместо известных числовых матриц вводим в уравнение буквы: первую матрицу обозначаем буквой A, вторую — буквой B. Неизвестную матрицу X оставляем. Это упрощение поможет составить формулу и выразить X через известную матрицу.
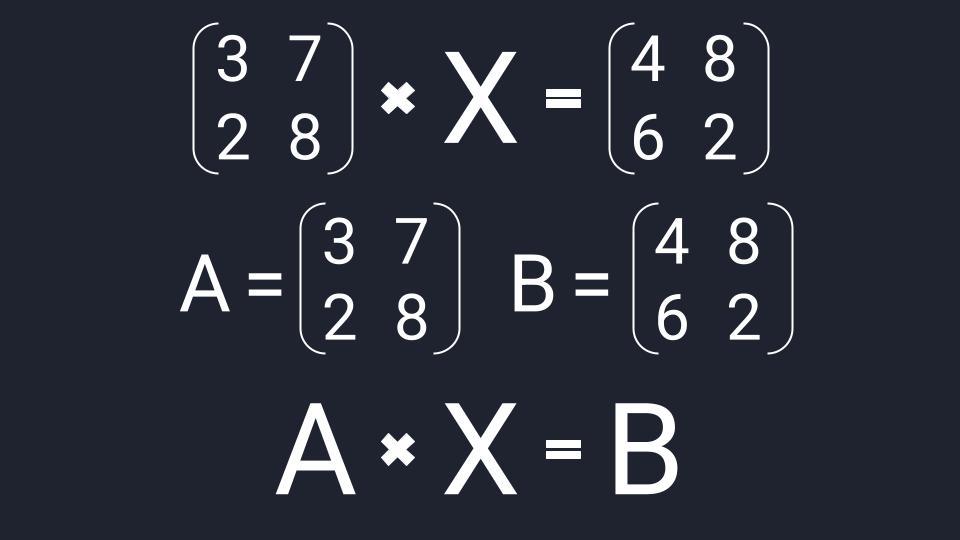
Видео:Решение матричных уравненийСкачать

Шаг 2. Вводим единичную матрицу
В линейной алгебре есть два вспомогательных понятия: обратная матрица и единичная матрица. Единичная матрица состоит из нулей, а по диагонали у неё единицы. Обратная матрица — это такая, которая при умножении на исходную даёт единичную матрицу.
Можно представить, что есть число 100 — это «сто в первой степени», 100 1
И есть число 0,01 — это «сто в минус первой степени», 100 -1
При перемножении этих двух чисел получится единица:
100 1 × 100 -1 = 100 × 0,01 = 1.
Вот такое, только в мире матриц.
Зная свойства единичных и обратных матриц, делаем алгебраическое колдунство. Умножаем обе известные матрицы на обратную матрицу А -1 . Неизвестную матрицу Х оставляем без изменений и переписываем уравнение:
А -1 × А × Х = А -1 × В
Добавляем единичную матрицу и упрощаем запись:
А -1 × А = E — единичная матрица
E × Х = А -1 × В — единичная матрица, умноженная на исходную матрицу, даёт исходную матрицу. Единичную матрицу убираем
Х = А -1 × В — новая запись уравнения
После введения единичной матрицы мы нашли способ выражения неизвестной матрицы X через известные матрицы A и B.
💡 Смотрите, что произошло: раньше нам нужно было найти неизвестную матрицу. А теперь мы точно знаем, как её найти: нужно рассчитать обратную матрицу A -1 и умножить её на известную матрицу B. И то и другое — замороченные процедуры, но с точки зрения арифметики — просто.
Видео:Как привести матрицу к ступенчатому виду - bezbotvyСкачать

Шаг 3. Находим обратную матрицу
Вспоминаем формулу и порядок расчёта обратной матрицы:
- Делим единицу на определитель матрицы A.
- Считаем транспонированную матрицу алгебраических дополнений.
- Перемножаем значения и получаем нужную матрицу.
Собираем формулу и получаем обратную матрицу. Для удобства умышленно оставляем перед матрицей дробное число, чтобы было проще считать.

Видео:Урок 1. Матрицы, определитель матрицы и ранг матрицы | Высшая математика | TutorOnlineСкачать

Шаг 4. Вычисляем неизвестную матрицу
Нам остаётся посчитать матрицу X: умножаем обратную матрицу А -1 на матрицу B. Дробь держим за скобками и вносим в матрицу только при условии, что элементы новой матрицы будут кратны десяти — их можно умножить на дробь и получить целое число. Если кратных элементов не будет — дробь оставим за скобками.

Видео:Обратная матрицаСкачать

Шаг 5. Проверяем уравнение
Мы решили матричное уравнение и получили красивый ответ с целыми числами. Выглядит правильно, но в случае с матрицами этого недостаточно. Чтобы проверить ответ, нам нужно вернуться к условию и умножить исходную матрицу A на матрицу X. В результате должна появиться матрица B. Если расчёты совпадут — мы всё сделали правильно. Если будут отличия — придётся решать заново.
👉 Часто начинающие математики пренебрегают финальной проверкой и считают её лишней тратой времени. Сегодня мы разобрали простое уравнение с двумя квадратными матрицами с четырьмя элементами в каждой. Когда элементов будет больше, в них легко запутаться и допустить ошибку.

Видео:Система линейных уравнений. Метод обратной матрицы. Матричный метод.Скачать

Ну и что
Алгоритм решения матричных уравнений несложный, если знать отдельные его компоненты. Дальше на основе этих компонентов математики переходят в более сложные пространства: работают с многомерными матрицами, решают более сложные уравнения, постепенно выходят на всё более и более абстрактные уровни. И дальше, в конце пути, появляется датасет из миллионов котиков. Этот датасет раскладывается на пиксели, каждый пиксель оцифровывается, цифры подставляются в матрицы, и уже огромный алгоритм в автоматическом режиме генерирует изображение нейрокотика:
Видео:Решение системы уравнений методом ГауссаСкачать

Сведение системы линейных уравнений к матрице.
Так система линейных уравнений
 | a 11 x 1 + a 12 x 2 + . + a 1 n x n = b 1 |
| a 21 x 1 + a 22 x 2 + . + a 2 n x n = b 2 | |
| ································ | |
| a m 1 x 1 + a m 2 x 2 + . + a mn x n = b m |
состоящая из m линейных уравнений, содержащая n неизвестных величин, может быть записана в виде матричного уравнения:
Матрица A — это матрица коэффициентов системы линейных уравнений, вектор-столбец x — вектор неизвестных, а вектор-столбец b — вектор значений системы линейных уравнений.
Видео:Как находить обратную матрицу - bezbotvyСкачать

Пример записи системы линейных уравнений с помощью матричного уравнения
Записать в виде матричном виде систему линейных уравнений:
 | 4 x 1 + x 2 — x 3 — x 4 = 3 |
| — x 1 + 3 x 3 — 2 x 4 = 5 | |
| 6 x 1 + 2 x 2 + 4 x 3 = 2 | |
| 2 x 2 — x 3 + x 4 = 0 |
Решение: Система линейных уравнений запишется с помощью матриц следующим образом:
Видео:Решение системы уравнений методом обратной матрицы - bezbotvyСкачать

Метод элементарных преобразований (методы Гаусса и Гаусса-Жордана для нахождения обратных матриц).
В первой части был рассмотрен способ нахождения обратной матрицы с помощью алгебраических дополнений. Здесь же мы опишем иной метод нахождения обратных матриц: с использованием элементарных преобразований.
Пусть нам задана квадратная матрица $A_<ntimes>$. Допишем справа к матрице $A$ единичную матрицу $E$ n-го порядка. После такого дописывания мы получим матрицу $left(A|Eright)$. Со строками этой матрицы можно выполнять такие преобразования:
- Смена мест двух строк.
- Умножение всех элементов строки на некоторое число, не равное нулю.
- Прибавление к элементам одной строки соответствующих элементов другой строки, умноженных на любой множитель.
Конечная цель указанных выше преобразований: привести матрицу $left(A|Eright)$ к такому виду: $left(E|A^right)$. Т.е. нужно сделать так, чтобы матрица до черты стала единичной, тогда после черты будет записана обратная матрица $A^$.
Добиться этой цели можно, выполняя над исходной матрицей $left(A|Eright)$ преобразования метода Гаусса или Гаусса-Жордана. Перед тем, как перейти к описанию этих методов, оговорим, что изначально матрица $A_<ntimes>$ не должна иметь нулевых строк или столбцов. Если в матрице $A$ есть хоть один нулевой столбец или нулевая строка, то обратная матрица $A^$ не существует.
Строки матрицы станем обозначать буквами $r$ (от слова «row»): $r_1$ – первая строка, $r_2$ – вторая строка и так далее.
Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Метод Гаусса
Этот метод делят на два этапа, которые называют прямым ходом и обратным.
Видео:Обратная матрица (2 способа нахождения)Скачать

Прямой ход метода Гаусса
В процессе выполнения прямого хода мы последовательно используем строки матрицы. На первом шаге работаем с первой строкой, на втором шаге – со второй и так далее. Если в ходе решения в матрице до черты возникла нулевая строка, то прекращаем преобразования, так как обратная матрица $A^$ не существует.
На первом шаге прямого хода обратимся к первой строке $r_1$. Если первый элемент $a_1$ первой строки не равен нулю, то выполняем обнуление всех ненулевых элементов первого столбца, лежащих под первой строкой. Если же $a_1=0$, то меняем местами первую строку с одной из тех нижележащих строк, у которых первый элемент отличен от нуля, а затем уже производим обнуление.
На втором шаге прямого хода обратимся к второй строке $r_2$. Если второй элемент $a_2$ второй строки не равен нулю, то выполняем обнуление всех ненулевых элементов второго столбца, лежащих под второй строкой. Если же $a_2=0$, то меняем местами вторую строку с одной из тех нижележащих строк, у которых второй элемент отличен от нуля, а затем уже производим обнуление. В случае, когда второй элемент равен нулю как у второй строки, так и у всех нижележащих строк, прекращаем решение, так как обратная матрица $A^$ не существует.
Полагаю, логика прямого хода ясна. На некоем k-м шаге мы работаем с строкой $r_k$. Если k-й элемент $a_k$ этой строки не равен нулю, то выполняем обнуление всех ненулевых элементов k-го столбца, лежащих под строкой $r_k$. Если же $a_k=0$, то меняем местами строку $r_k$ с одной из тех нижележащих строк, у которых k-й элемент отличен от нуля, а затем уже производим обнуление. В случае, когда k-й элемент равен нулю как у строки $r_k$, так и у всех нижележащих строк, прекращаем решение, так как обратная матрица $A^$ не существует.
Когда мы придём к последней строке, матрица до черты станет верхней треугольной, т.е. все элементы под главной диагональю будут равны нулю. Это будет означать конец прямого хода метода Гаусса.
Видео:Элементарные преобразования матриц. Высшая математика.Скачать

Обратный ход метода Гаусса
На этом этапе мы поднимаемся по матрице «снизу вверх». Сначала используем последнюю строку $r_n$, затем предпоследнюю $r_$ и так далее, пока не дойдём до первой строки. С каждой строкой выполняем однотипные операции.
Пусть, например, речь идёт о некоей k-й строке. Матрица, расположенная до черты, содержит в строке $r_k$ диагональный элемент $a_$. Если $a_=1$, то это нас вполне устраивает, а если $a_neq$, то просто умножаем строку $r_k$ на коэффициент $frac<a_>$, чтобы диагональный элемент стал равен 1. Затем с помощью строки $r_k$ обнуляем элементы k-го столбца, расположенные над строкой $r_k$.
Как только мы дойдём до первой строки, матрица до черты станет единичной, и алгоритм завершится.
Видео:11. Ранг матрицыСкачать

Метод Гаусса-Жордана
Последовательно используем строки матрицы. На первом шаге работаем с первой строкой, на втором шаге – со второй и так далее. Если в ходе решения в матрице до черты возникла нулевая строка, то прекращаем преобразования, так как обратная матрица $A^$ не существует.
На первом шаге прямого хода обратимся к первой строке $r_1$. Первый элемент этой строки обозначим как $a_1$. Если $a_1=0$, то меняем местами первую строку с одной из тех нижележащих строк, у которых первый элемент отличен от нуля. Затем, если $a_1neq$, умножаем строку $r_1$ на $frac$ (если $a_1=1$, то никакого домножения делать не надо). Далее с помощью строки $r_1$ производим обнуление всех остальных ненулевых элементов первого столбца, после чего переходим к следующему шагу.
На втором шаге прямого хода работаем с второй строкой $r_2$. Второй элемент этой строки обозначим как $a_2$. Если $a_2=0$, то меняем местами вторую строку с одной из тех нижележащих строк, у которых второй элемент отличен от нуля. Если таких строк нет, т.е. у всех нижележащих строк второй элемент равен нулю, то прекращаем решение, так как обратная матрица $A^$ не существует. Затем, если $a_2neq$, умножаем строку $r_2$ на $frac$ (если $a_2=1$, то никакого домножения делать не надо). Далее с помощью строки $r_2$ производим обнуление всех остальных ненулевых элементов второго столбца, после чего переходим к следующему шагу.
Полагаю, логика данного метода ясна. На k-м шаге работаем с k-й строкой $r_k$, k-й элемент которой обозначим как $a_k$. Если $a_k=0$, то меняем местами строку $r_k$ с одной из тех нижележащих строк, у которых k-й элемент отличен от нуля. Если таких строк нет, т.е. у всех нижележащих строк k-й элемент равен нулю, то прекращаем решение, так как обратная матрица $A^$ не существует. Затем, если $a_kneq$, умножаем строку $r_k$ на $frac$ (если $a_k=1$, то никакого домножения делать не надо). Далее с помощью строки $r_k$ производим обнуление всех остальных ненулевых элементов k-го столбца, после чего переходим к следующему шагу.
Когда мы обработаем последнюю строку, матрица до черты станет единичной, и алгоритм завершится.
Перед тем, как переходить к примерам, я введу один дополнительный термин: ведущий элемент. Ведущим элементом ненулевой строки называется её первый (считая слева направо) отличный от нуля элемент. Например, в строке $(0;0;5;-9;0)$ ведущим будет третий элемент (он равен 5).
Найти матрицу $A^$, если $A=left(begin -5 & 23 & -24\ -1 & 4 & -5\ 9 & -40 & 43 end right)$.
Заданная нам матрица не имеет нулевых строк или столбцов, поэтому можем приступать к нахождению $A^$. Поставленную задачу решим двумя способами: как преобразованиями метода Гаусса, так и метода Гаусса-Жордана. Для начала запишем матрицу $(A|E)$, которая в нашем случае будет иметь такой вид:
$$ left(begin -5 & 23 & -24 & 1 & 0 & 0\ -1 & 4 & -5 & 0 & 1 & 0\ 9 & -40 & 43 & 0 & 0 & 1 endright) $$
Наша цель: привести матрицу $(A|E)$ к виду $left(E|A^right)$.
Видео:Нахождение обратной матрицы с помощью элементарных преобразованийСкачать

Метод Гаусса
Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Прямой ход метода Гаусса
На первом шаге прямого хода мы работаем с первой строкой. Первый элемент этой строки (число -5) не равен нулю, поэтому можем приступать к обнулению ненулевых элементов первого столбца, расположенных под первой строкой. Однако для тех преобразований, которые мы станем делать для обнуления элементов, удобно, когда ведущий элемент используемой строки равен 1 или -1. Почему это так, станет ясно из дальнейших действий. Чтобы ведущий элемент текущей строки стал равен -1, поменяем местами первую строку с одной из нижележащих строк – с второй строкой:
$$ left(begin -5 & 23 & -24 & 1 & 0 & 0\ -1 & 4 & -5 & 0 & 1 & 0\ 9 & -40 & 43 & 0 & 0 & 1 endright) overset<r_1leftrightarrow> left(begin boldred & 4 & -5 & 0 & 1 & 0\ normblue & 23 & -24 & 1 & 0 & 0\ normblue & -40 & 43 & 0 & 0 & 1 endright) $$
Теперь ведущий элемент первой строки стал равен -1 (я выделил этот элемент красным цветом). Приступим к обнулению ненулевых элементов первого столбца, лежащих под первой строкой (они выделены синим цветом). Для этого над строками матрицы нужно выполнить такие действия:
Запись $r_2-5r_1$ означает, что от элементов второй строки вычли соответствующие элементы первой строки, умноженные на пять. Результат записывают на место второй строки в новую матрицу. Если с устным выполнением такой операции возникают сложности, то это действие можно выполнить отдельно:
Действие $r_3+9r_1$ выполняется аналогично. Первую строку мы не трогали, поэтому в новую матрицу она перейдёт без изменений:
$$ left(begin -1 & 4 & -5 & 0 & 1 & 0\ -5 & 23 & -24 & 1 & 0 & 0\ 9 & -40 & 43 & 0 & 0 & 1 endright) begin phantom\ r_2-5r_1 \ r_3+9r_1 end rightarrow left(begin -1 & 4 & -5 & 0 & 1 & 0\ 0 & 3 & 1 & 1 & -5 & 0\ 0 & -4 & -2 & 0 & 9 & 1 endright) $$
На этом первый шаг закончен. Нулевых строк в матрице до черты не возникло, поэтому продолжаем решение. Кстати, теперь, я полагаю, ясно, зачем надо было менять местами строки. Если бы не смена мест строк, нам пришлось бы выполнять действия $r_2-fraccdot$ и $r_3+fraccdot$, что привело бы к появлению дробей. А легче, разумеется, работать с целыми числами, чем с дробями.
На втором шаге прямого хода мы работаем с второй строкой. Второй элемент этой строки (число 3) не равен нулю, поэтому можем приступать к обнулению ненулевых элементов второго столбца, расположенных под второй строкой:
$$ left(begin -1 & 4 & -5 & 0 & 1 & 0\ 0 & 3 & 1 & 1 & -5 & 0\ 0 & -4 & -2 & 0 & 9 & 1 endright) begin phantom\ phantom \ r_3+4/3cdot end rightarrow left(begin -1 & 4 & -5 & 0 & 1 & 0\ 0 & 3 & 1 & 1 & -5 & 0\ 0 & 0 & -2/3 & 4/3 & 7/3 & 1 endright) $$
Матрица до черты стала верхней треугольной, поэтому прямой ход метода Гаусса окончен.
Пару слов насчёт действий со строками, которые мы выполняли на втором шаге. На первом шаге мы меняли местами строки, чтобы ведущий элемент первой строки стал равен -1. Здесь такая смена строк ничего не даст, так как доступна к обмену лишь третья строка, а у неё ведущий элемент тоже не равен ни 1, ни -1. В этом случае можно выполнить дополнительное преобразование со второй строкой: $r_2+r_3$:
$$ left(begin -1 & 4 & -5 & 0 & 1 & 0\ 0 & 3 & 1 & 1 & -5 & 0\ 0 & -4 & -2 & 0 & 9 & 1 endright) begin phantom\ r_2+r_3 \ phantom end rightarrow left(begin -1 & 4 & -5 & 0 & 1 & 0\ 0 & -1 & -1 & 1 & 4 & 1\ 0 & -4 & -2 & 0 & 9 & 1 endright) $$
После этого текущий шаг прямого хода будет продолжен без дробей. Можно было сделать и такое действие: $3r_3+4r_2$, тогда и необходимый элемент третьего столбца был бы обнулён, и дробей бы не появилось. Выполнять такие действия или нет – надо смотреть по ситуации. Если работы с дробями предвидится немного, то особого смысла в попытках их избежать нет. Если же нас ожидают ещё несколько шагов прямого хода, то, возможно, лучше упростить себе расчёты и выполнить вспомогательное действие, чтобы потом не работать с дробями. К слову, если есть необходимость избавиться от дробей в некоей строке, то можно просто домножить данную строку на соответствующий коэффициент. Например, строку $left(frac;;-frac;;2;0right)$ можно домножить на число 15, тогда дроби исчезнут, и строка станет такой: $left(5;;-12;;30;0right)$.
Видео:Линейная алгебра, Матрицы: Метод Гаусса. Высшая математикаСкачать

Обратный ход метода Гаусса
На первом шаге обратного хода мы работаем с последней, т.е. третьей строкой матрицы. Посмотрим на диагональный элемент в третьей строке: он равен $-frac$. Сделаем этот элемент единицей, домножив третью строку на $-frac$, а затем с помощью третьей строки обнулим ненулевые элементы третьего столбца, расположенные над третьей строкой:
$$ left(begin -1 & 4 & -5 & 0 & 1 & 0\ 0 & 3 & 1 & 1 & -5 & 0\ 0 & 0 & -2/3 & 4/3 & 7/3 & 1 endright) begin phantom\ phantom\ -3/2cdot end rightarrow\ left(begin -1 & 4 & -5 & 0 & 1 & 0\ 0 & 3 & 1 & 1 & -5 & 0\ 0 & 0 & 1 & -2 & -7/2 & -3/2 endright) begin r_1+5r_3 phantom\ r_2-r_3\ phantom end rightarrow left(begin -1 & 4 & 0 & -10 & -33/2 & -15/2\ 0 & 3 & 0 & 3 & -3/2 & 3/2\ 0 & 0 & 1 & -2 & -7/2 & -3/2 endright) $$
На втором шаге обратного хода мы работаем с предпоследней, т.е. второй строкой матрицы. Посмотрим на диагональный элемент во второй строке: он равен 3. Сделаем этот элемент единицей, домножив вторую строку на $frac$, а затем с помощью второй строки обнулим ненулевой элемент второго столбца, расположенный над второй строкой:
$$ left(begin -1 & 4 & 0 & -10 & -33/2 & -15/2\ 0 & 3 & 0 & 3 & -3/2 & 3/2\ 0 & 0 & 1 & -2 & -7/2 & -3/2 endright) begin phantom\ 1/3cdot \ phantom end rightarrow\ left(begin -1 & 4 & 0 & -10 & -33/2 & -15/2\ 0 & 1 & 0 & 1 & -1/2 & 1/2\ 0 & 0 & 1 & -2 & -7/2 & -3/2 endright) begin r_1-4r_2\ phantom \ phantom end rightarrow left(begin -1 & 0 & 0 & -14 & -29/2 & -19/2\ 0 & 1 & 0 & 1 & -1/2 & 1/2\ 0 & 0 & 1 & -2 & -7/2 & -3/2 endright) $$
Работаем с первой строкой. Сделаем диагональный элемент в первой строке (число -1) равным единице, домножив первую строку на -1:
$$ left(begin -1 & 0 & 0 & -14 & -29/2 & -19/2\ 0 & 1 & 0 & 1 & -1/2 & 1/2\ 0 & 0 & 1 & -2 & -7/2 & -3/2 endright) begin -1cdot\ phantom \ phantom end rightarrow left(begin 1 & 0 & 0 & 14 & 29/2 & 19/2\ 0 & 1 & 0 & 1 & -1/2 & 1/2\ 0 & 0 & 1 & -2 & -7/2 & -3/2 endright) $$
Матрица до черты стала единичной, преобразования завершены. Обратная матрица будет такой:
$$ A^ =left(begin 14 & 29/2 & 19/2\ 1 & -1/2 & 1/2\ -2 & -7/2 & -3/2 endright) $$
Если пропустить все пояснения, то решение будет таким:
$$ left(begin -5 & 23 & -24 & 1 & 0 & 0\ -1 & 4 & -5 & 0 & 1 & 0\ 9 & -40 & 43 & 0 & 0 & 1 endright) overset<r_1leftrightarrow> $$ $$ rightarrowleft(begin -1 & 4 & -5 & 0 & 1 & 0\ -5 & 23 & -24 & 1 & 0 & 0\ 9 & -40 & 43 & 0 & 0 & 1 endright) begin phantom\ r_2-5r_1 \ r_3+9r_1 end rightarrow left(begin -1 & 4 & -5 & 0 & 1 & 0\ 0 & 3 & 1 & 1 & -5 & 0\ 0 & -4 & -2 & 0 & 9 & 1 endright) begin phantom\ phantom \ r_3+4/3cdot end rightarrow $$ $$ rightarrowleft(begin -1 & 4 & -5 & 0 & 1 & 0\ 0 & 3 & 1 & 1 & -5 & 0\ 0 & 0 & -2/3 & 4/3 & 7/3 & 1 endright) begin phantom\ phantom\ -3/2cdot end rightarrow left(begin -1 & 4 & -5 & 0 & 1 & 0\ 0 & 3 & 1 & 1 & -5 & 0\ 0 & 0 & 1 & -2 & -7/2 & -3/2 endright) begin r_1+5r_3 phantom\ r_2-r_3\ phantom end rightarrow $$ $$ rightarrowleft(begin -1 & 4 & 0 & -10 & -33/2 & -15/2\ 0 & 3 & 0 & 3 & -3/2 & 3/2\ 0 & 0 & 1 & -2 & -7/2 & -3/2 endright) begin phantom\ 1/3cdot \ phantom end rightarrow left(begin -1 & 4 & 0 & -10 & -33/2 & -15/2\ 0 & 1 & 0 & 1 & -1/2 & 1/2\ 0 & 0 & 1 & -2 & -7/2 & -3/2 endright) begin r_1-4r_2\ phantom \ phantom end rightarrow $$ $$ rightarrowleft(begin -1 & 0 & 0 & -14 & -29/2 & -19/2\ 0 & 1 & 0 & 1 & -1/2 & 1/2\ 0 & 0 & 1 & -2 & -7/2 & -3/2 endright) begin -1cdot\ phantom \ phantom end rightarrow left(begin 1 & 0 & 0 & 14 & 29/2 & 19/2\ 0 & 1 & 0 & 1 & -1/2 & 1/2\ 0 & 0 & 1 & -2 & -7/2 & -3/2 endright) $$
Теперь решим этот же пример методом Гаусса-Жордана.
Видео:Решение системы уравнений методом обратной матрицы.Скачать

Метод Гаусса-Жордана
На первом шаге мы работаем с первой строкой. Первый элемент этой строки (число -5) не равен нулю, поэтому можем следовать стандартному алгоритму: домножить первую строку на $-frac$, чтобы первый элемент стал равен единице, а затем обнулить все иные ненулевые элементы первого столбца. Однако, как и при решении методом Гаусса, удобно, когда ведущий элемент используемой строки равен 1 или -1. Поэтому как и на первом шаге метода Гаусса, поменяем местами первую строку с второй строкой:
$$ left(begin -5 & 23 & -24 & 1 & 0 & 0\ -1 & 4 & -5 & 0 & 1 & 0\ 9 & -40 & 43 & 0 & 0 & 1 endright) overset<r_1leftrightarrow> left(begin -1 & 4 & -5 & 0 & 1 & 0\ normblue & 23 & -24 & 1 & 0 & 0\ normblue & -40 & 43 & 0 & 0 & 1 endright) $$
Теперь первый элемент первой строки стал равен -1. Чтобы этот элемент стал равен 1, домножим первую строку на -1, а потом обнулим все остальные ненулевые элементы первого столбца (они выделены в матрице выше синим цветом):
$$ left(begin -1 & 4 & -5 & 0 & 1 & 0\ -5 & 23 & -24 & 1 & 0 & 0\ 9 & -40 & 43 & 0 & 0 & 1 endright) begin -1cdot\ phantom \ phantom end rightarrow\ rightarrowleft(begin 1 & -4 & 5 & 0 & -1 & 0\ -5 & 23 & -24 & 1 & 0 & 0\ 9 & -40 & 43 & 0 & 0 & 1 endright) begin phantom\ r_2+5r_1 \ r_3-9r_1 end rightarrow left(begin 1 & -4 & 5 & 0 & -1 & 0\ 0 & 3 & 1 & 1 & -5 & 0\ 0 & -4 & -2 & 0 & 9 & 1 endright) $$
На этом первый шаг закончен. Нулевых строк в матрице до черты не возникло, поэтому продолжаем решение.
На втором шаге мы работаем с второй строкой. Второй элемент этой строки (число 3) не равен нулю, поэтому домножаем вторую строку на $frac$, чтобы второй элемент стал равен единице, а затем обнуляем все иные ненулевые элементы второго столбца.
$$ left(begin 1 & -4 & 5 & 0 & -1 & 0\ 0 & 3 & 1 & 1 & -5 & 0\ 0 & -4 & -2 & 0 & 9 & 1 endright) begin phantom\1/3cdot \phantomend rightarrow\ rightarrowleft(begin 1 & -4 & 5 & 0 & -1 & 0\ 0 & 1 & 1/3 & 1/3 & -5/3 & 0\ 0 & -4 & -2 & 0 & 9 & 1 endright) begin r_1+4r_2\ phantom \ r_3+4r_2 end rightarrow left(begin 1 & 0 & 19/3 & 4/3 & -23/3 & 0\ 0 & 1 & 1/3 & 1/3 & -5/3 & 0\ 0 & 0 & -2/3 & 4/3 & 7/3 & 1 endright) $$
Замечание относительно облегчения работы с дробями, сделанное после второго шага прямого хода метода Гаусса, остаётся в силе и здесь.
На третьем шаге мы работаем с третьей строкой. Третий элемент этой строки (число -2/3) не равен нулю, поэтому домножаем третью строку на $-frac$, чтобы третий элемент стал равен единице, а затем обнуляем все иные ненулевые элементы третьего столбца.
$$ left(begin 1 & 0 & 19/3 & 4/3 & -23/3 & 0\ 0 & 1 & 1/3 & 1/3 & -5/3 & 0\ 0 & 0 & -2/3 & 4/3 & 7/3 & 1 endright) begin phantom\phantom \ -3/2cdotend rightarrow\ rightarrowleft(begin 1 & 0 & 19/3 & 4/3 & -23/3 & 0\ 0 & 1 & 1/3 & 1/3 & -5/3 & 0\ 0 & 0 & 1 & -2 & -7/2 & -3/2 endright) begin r_1-19/3r_3\ r_2-1/3cdot \ phantom end rightarrow left(begin 1 & 0 & 0 & 14 & 29/2 & 19/2\ 0 & 1 & 0 & 1 & -1/2 & 1/2\ 0 & 0 & 1 & -2 & -7/2 & -3/2 endright) $$
Матрица до черты стала единичной, преобразования завершены. Обратная матрица будет такой:
$$ A^ =left(begin 14 & 29/2 & 19/2\ 1 & -1/2 & 1/2\ -2 & -7/2 & -3/2 endright) $$
Если пропустить все пояснения, то решение будет таким:
$$ left(begin -5 & 23 & -24 & 1 & 0 & 0\ -1 & 4 & -5 & 0 & 1 & 0\ 9 & -40 & 43 & 0 & 0 & 1 endright) overset<r_1leftrightarrow> left(begin -1 & 4 & -5 & 0 & 1 & 0\ -5 & 23 & -24 & 1 & 0 & 0\ 9 & -40 & 43 & 0 & 0 & 1 endright) begin -1cdot\ phantom \ phantom end rightarrow $$ $$ rightarrowleft(begin 1 & -4 & 5 & 0 & -1 & 0\ -5 & 23 & -24 & 1 & 0 & 0\ 9 & -40 & 43 & 0 & 0 & 1 endright) begin phantom\ r_2+5r_1 \ r_3-9r_1 end rightarrow left(begin 1 & -4 & 5 & 0 & -1 & 0\ 0 & 3 & 1 & 1 & -5 & 0\ 0 & -4 & -2 & 0 & 9 & 1 endright) begin phantom\1/3cdot \phantomend rightarrow $$ $$ rightarrowleft(begin 1 & -4 & 5 & 0 & -1 & 0\ 0 & 1 & 1/3 & 1/3 & -5/3 & 0\ 0 & -4 & -2 & 0 & 9 & 1 endright) begin r_1+4r_2\ phantom \ r_3+4r_2 end rightarrow left(begin 1 & 0 & 19/3 & 4/3 & -23/3 & 0\ 0 & 1 & 1/3 & 1/3 & -5/3 & 0\ 0 & 0 & -2/3 & 4/3 & 7/3 & 1 endright) begin phantom\phantom \ -3/2cdotend rightarrow $$ $$ rightarrowleft(begin 1 & 0 & 19/3 & 4/3 & -23/3 & 0\ 0 & 1 & 1/3 & 1/3 & -5/3 & 0\ 0 & 0 & 1 & -2 & -7/2 & -3/2 endright) begin r_1-19/3r_3\ r_2-1/3cdot \ phantom end rightarrow left(begin 1 & 0 & 0 & 14 & 29/2 & 19/2\ 0 & 1 & 0 & 1 & -1/2 & 1/2\ 0 & 0 & 1 & -2 & -7/2 & -3/2 endright) $$
Ответ: $A^ =left(begin 14 & 29/2 & 19/2\ 1 & -1/2 & 1/2\ -2 & -7/2 & -3/2 endright)$.
Найти матрицу $A^$, если $A=left(begin -2 & 3 & 0 & 1\ -6 & 9 & -2 & 7\ 0 & -2 & -18 & 27\ -4 & 5 & -8 & 14end right)$.
В предыдущем примере были даны подробные пояснения каждого шага как метода Гаусса, так и метода Гаусса-Жордана. В этом примере я стану комментировать лишь некие нюансы, которые возникнут в ходе решения.
Видео:§22 Элементарные преобразования матрицСкачать

Метод Гаусса
Пора переходить ко второму шагу прямого хода метода Гаусса. На этом шаге должна использоваться вторая строка, однако второй элемент данной строки равен нулю. Согласно алгоритму, нужно поменять местами вторую строку с одной из нижележащих строк, у которых второй элемент отличен от нуля. Поменяем местами вторую и четвёртую строки, а потом продолжим преобразования:
$$ left(begin -2 & 3 & 0 & 1 & 1 & 0 & 0 & 0\ 0 & 0 & -2 & 4 & -3 & 1 & 0 & 0 \ 0 & -2 & -18 & 27 & 0 & 0 & 1 & 0\ 0 & -1 & -8 & 12 & -2 & 0 & 0 & 1 end right) overset<r_2leftrightarrow> left(begin -2 & 3 & 0 & 1 & 1 & 0 & 0 & 0\ 0 & -1 & -8 & 12 & -2 & 0 & 0 & 1\ 0 & -2 & -18 & 27 & 0 & 0 & 1 & 0\ 0 & 0 & -2 & 4 & -3 & 1 & 0 & 0 end right) begin phantom \ phantom \ r_3-2r_2 \ phantom end rightarrow $$ $$ rightarrowleft(begin -2 & 3 & 0 & 1 & 1 & 0 & 0 & 0\ 0 & -1 & -8 & 12 & -2 & 0 & 0 & 1\ 0 & 0 & -2 & 3 & 4 & 0 & 1 & -2\ 0 & 0 & -2 & 4 & -3 & 1 & 0 & 0 end right) begin phantom \ phantom \ phantom \ r_4-r_3 end rightarrow $$ $$ rightarrowleft(begin -2 & 3 & 0 & 1 & 1 & 0 & 0 & 0\ 0 & -1 & -8 & 12 & -2 & 0 & 0 & 1\ 0 & 0 & -2 & 3 & 4 & 0 & 1 & -2\ 0 & 0 & 0 & 1 & -7 & 1 & -1 & 2 end right) begin r_1-r_4 \ r_2-12r_4 \ r_3-3r_1 \ phantom end rightarrow $$ $$ rightarrowleft(begin -2 & 3 & 0 & 0 & 8 & -1 & 1 & -2\ 0 & -1 & -8 & 0 & 82 & -12 & 12 & -23\ 0 & 0 & -2 & 0 & 25 & -3 & 4 & -8\ 0 & 0 & 0 & 1 & -7 & 1 & -1 & 2 end right) begin phantom \ phantom \ -1/2cdot \ phantom end rightarrow $$ $$ rightarrowleft(begin -2 & 3 & 0 & 0 & 8 & -1 & 1 & -2\ 0 & -1 & -8 & 0 & 82 & -12 & 12 & -23\ 0 & 0 & 1 & 0 & -25/2 & 3/2 & -2 & 4\ 0 & 0 & 0 & 1 & -7 & 1 & -1 & 2 end right) begin phantom \ r_2+8r_3 \ phantom \ phantom end rightarrow $$ $$ rightarrowleft(begin -2 & 3 & 0 & 0 & 8 & -1 & 1 & -2\ 0 & -1 & 0 & 0 & -18 & 0 & -4 & 9\ 0 & 0 & 1 & 0 & -25/2 & 3/2 & -2 & 4\ 0 & 0 & 0 & 1 & -7 & 1 & -1 & 2 end right) begin phantom \ -1cdot \ phantom \ phantom end rightarrow $$ $$ rightarrowleft(begin -2 & 3 & 0 & 0 & 8 & -1 & 1 & -2\ 0 & 1 & 0 & 0 & 18 & 0 & 4 & -9\ 0 & 0 & 1 & 0 & -25/2 & 3/2 & -2 & 4\ 0 & 0 & 0 & 1 & -7 & 1 & -1 & 2 end right) begin r_1-3r_2 \ phantom \ phantom \ phantom end rightarrow $$ $$ rightarrowleft(begin -2 & 0 & 0 & 0 & -46 & -1 & -11 & 25\ 0 & 1 & 0 & 0 & 18 & 0 & 4 & -9\ 0 & 0 & 1 & 0 & -25/2 & 3/2 & -2 & 4\ 0 & 0 & 0 & 1 & -7 & 1 & -1 & 2 end right) begin -1/2cdot \ phantom \ phantom \ phantom end rightarrow $$ $$ rightarrowleft(begin 1 & 0 & 0 & 0 & 23 & 1/2 & 11/2 & -25/2\ 0 & 1 & 0 & 0 & 18 & 0 & 4 & -9\ 0 & 0 & 1 & 0 & -25/2 & 3/2 & -2 & 4\ 0 & 0 & 0 & 1 & -7 & 1 & -1 & 2 endright) $$
Из последней матрицы получаем ответ:
$$ A^ =left(begin 23 & 1/2 & 11/2 & -25/2\ 18 & 0 & 4 & -9\ -25/2 & 3/2 & -2 & 4\ -7 & 1 & -1 & 2 endright) $$
Метод Гаусса-Жордана
Пора переходить ко второму шагу метода Гаусса-Жордана. На этом шаге должна использоваться вторая строка, однако второй элемент данной строки равен нулю. Согласно алгоритму, нужно поменять местами вторую строку с одной из нижележащих строк, у которых второй элемент отличен от нуля. Поменяем местами вторую и четвёртую строки, а потом продолжим преобразования:
$$ left(begin 1 & -3/2 & 0 & -1/2 & -1/2 & 0 & 0 & 0\ 0 & 0 & -2 & 4 & -3 & 1 & 0 & 0 \ 0 & -2 & -18 & 27 & 0 & 0 & 1 & 0\ 0 & -1 & -8 & 12 & -2 & 0 & 0 & 1 end right) overset<r_2leftrightarrow> $$ $$ rightarrowleft(begin 1 & -3/2 & 0 & -1/2 & -1/2 & 0 & 0 & 0\ 0 & -1 & -8 & 12 & -2 & 0 & 0 & 1 \ 0 & -2 & -18 & 27 & 0 & 0 & 1 & 0\ 0 & 0 & -2 & 4 & -3 & 1 & 0 & 0 end right) begin phantom \ -1cdot \ phantom \ phantom end rightarrow $$ $$ rightarrowleft(begin 1 & -3/2 & 0 & -1/2 & -1/2 & 0 & 0 & 0\ 0 & 1 & 8 & -12 & 2 & 0 & 0 & -1 \ 0 & -2 & -18 & 27 & 0 & 0 & 1 & 0\ 0 & 0 & -2 & 4 & -3 & 1 & 0 & 0 end right) begin r_1+3/2cdot \ phantom \ r_3+2r_2 \ phantom end rightarrow $$ $$ rightarrowleft(begin 1 & 0 & 12 & -37/2 & 5/2 & 0 & 0 & -3/2\ 0 & 1 & 8 & -12 & 2 & 0 & 0 & -1 \ 0 & 0 & -2 & 3 & 4 & 0 & 1 & -2\ 0 & 0 & -2 & 4 & -3 & 1 & 0 & 0 end right) begin phantom \ phantom \ -1/2cdot \ phantom end rightarrow $$ $$ rightarrowleft(begin 1 & 0 & 12 & -37/2 & 5/2 & 0 & 0 & -3/2\ 0 & 1 & 8 & -12 & 2 & 0 & 0 & -1 \ 0 & 0 & 1 & -3/2 & -2 & 0 & -1/2 & 1\ 0 & 0 & -2 & 4 & -3 & 1 & 0 & 0 end right) begin r_1-12r_3 \ r_2-8r_3 \ phantom \ r_4+2r_3 end rightarrow $$ $$ rightarrowleft(begin 1 & 0 & 0 & -1/2 & 53/2 & 0 & 6 & -27/2\ 0 & 1 & 0 & 0 & 18 & 0 & 4 & -9 \ 0 & 0 & 1 & -3/2 & -2 & 0 & -1/2 & 1\ 0 & 0 & 0 & 1 & -7 & 1 & -1 & 2 end right) begin r_1+1/2cdot \ phantom \ r_3+3/2cdot \ phantom end rightarrow $$ $$ rightarrowleft(begin 1 & 0 & 0 & 0 & 23 & 1/2 & 11/2 & -25/2\ 0 & 1 & 0 & 0 & 18 & 0 & 4 & -9\ 0 & 0 & 1 & 0 & -25/2 & 3/2 & -2 & 4\ 0 & 0 & 0 & 1 & -7 & 1 & -1 & 2 endright) $$
Из последней матрицы получаем ответ:
$$ A^ =left(begin 23 & 1/2 & 11/2 & -25/2\ 18 & 0 & 4 & -9\ -25/2 & 3/2 & -2 & 4\ -7 & 1 & -1 & 2 endright) $$
Ответ: $ A^ =left(begin 23 & 1/2 & 11/2 & -25/2\ 18 & 0 & 4 & -9\ -25/2 & 3/2 & -2 & 4\ -7 & 1 & -1 & 2 endright) $.
Найти матрицу $A^$, если $A=left(begin 1 & -2 & 5\ -2 & 5 & -13\ -3 & 4 & -9end right)$.
В данном примере применим метод Гаусса.
$$ left(begin 1 & -2 & 5 & 1 & 0 & 0\ -2 & 5 & -13 & 0 & 1 & 0\ -3 & 4 & -9 & 0 & 0 & 1end right) begin phantom \ r_2+2r_1 \ r_3+3r_1 end rightarrow\ $$ $$ rightarrowleft(begin 1 & -2 & 5 & 1 & 0 & 0\ 0 & 1 & -3 & 2 & 1 & 0\ 0 & -2 & 6 & 3 & 0 & 1end right) begin phantom \ phantom \ r_3+2r_2 end rightarrow left(begin 1 & -2 & 5 & 1 & 0 & 0\ 0 & 1 & -3 & 2 & 1 & 0\ 0 & 0 & 0 & 7 & 2 & 1endright) $$
В матрице до черты появилась нулевая строка. Это означает, что обратная матрица $A^$ не существует.
Ответ: обратной матрицы не существует.