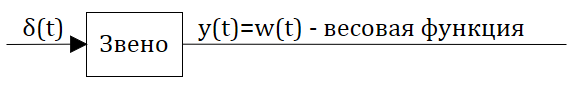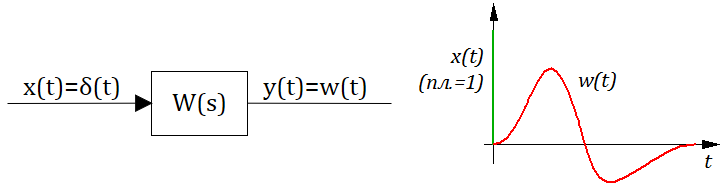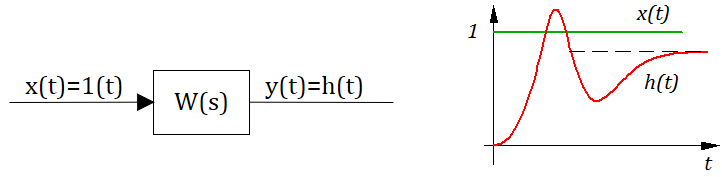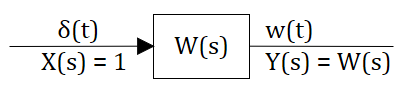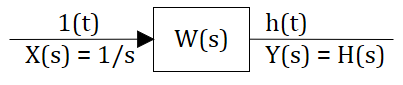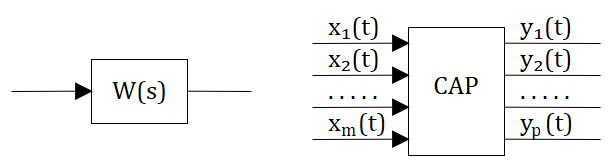Как преобразовать дифференциальное уравнение в передаточную функцию

ИССЛЕДОВАНИЕ ВРЕМЕННЫХ ХАРАКТЕРИСТИК

ДИНАМИЧЕСКИХ ЗВЕНЬЕВ И ИХ СОЕДИНЕНИЙ

Цель работы: для звеньев, заданных передаточными функциями, выбираемыми из табл. 1 прил. 2, и их соединений выполнить следующее:

1) вывести аналитические выражения кривой разгона и импульсной переходной характеристик;

2) построить графические зависимости полученных характеристик при различных значениях постоянных времени и коэффициентов усиления.

Параметры звеньев выбираются из табл. 2 прил. 2 в зависимости от варианта, задаваемого преподавателем.

2.1 Теоретические сведения

Системы автоматического регулирования (САР) принято изображать в виде структурных схем. Структурная схема – это условное изображение, в котором отдельные элементы системы представляются прямоугольниками, а связи между элементами изображаются стрелками, показывающими направление передачи сигнала, н ад которыми ставится условное обозначение сигнала.

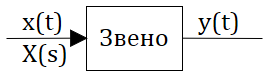
Для создания общей методики расчета различных САР было введено понятие динамического звена. Типовым звеном системы автоматического регулирования является составной элемент, имеющий один вход и один выход, и описываемый дифференциальным уравнением не выше второго порядка. На структурной схеме объектов управления звенья изображаются в виде прямоугольников, внутри которых записывается передаточная функция звена (рис. 1).

Рисунок 1. Пример изображения звена на структурных схемах

Одной из основных динамических характеристик объекта, широко используемых в теории автоматического регулирования, является передаточная функция.

Передаточной функцией объекта называется отношение преобразованного по Лапласу выхода объекта у ( р ) к преобразованному по Лапласу входу х ( р ) при нулевых начальных условиях. Передаточная функция является функцией комплексного переменного p , обозначается W ( p ): . Передаточная функция характеризует динамику объекта по определенному каналу, связывающему вход объекта с выходом. Если в объекте имеется несколько входов, то каждому каналу связи входа с выходом будет соответствовать своя передаточная функция.

Так же, как и дифференциальное уравнение, передаточная функция полностью характеризует динамику объекта. Если задано дифференциальное уравнение объекта, то для получения передаточной функции необходимо преобразовать дифференциальное уравнение по Лапласу и из полученного алгебраического уравнения найти соотношение .

Если известна передаточная функция объекта, то изображение выхода объекта у ( р ) равно произведению передаточной функции на изображение входа х ( р ): .

Любая самая сложная структурная схема может быть изображена с помощью трех основных типов соединения: — параллельного (рис. 2); — последовательного и соединения с обратной связью.

Рисунок 2. Структурная схема параллельного соединения звеньев

При параллельном соединении входные сигналы всех звеньев одинаковы и равны входу системы х ( р ), а выход системы у( р ) равен сумме выходов звеньев.

Запишем уравнения выходных координат каждого звена:

;

;

.

Выход всей системы будет равен

Передаточная функция системы: .

Передаточная функция системы параллельно соединенных звеньев равна сумме передаточных функций отдельных звеньев.

Последовательное соединение звеньев. Особенностью является то, что выход предыдущего звена является входом последующего (рис. 3).

Рисунок 3. Структурная схема последовательного соединения звеньев

Уравнения выходных сигналов каждого звеньев имеют вид:

;

;

.

Выходной сигнал последнего звена является выходом всей системы , передаточная функция системы:

.

Таким образом, передаточная функция системы последовательно соединенных звеньев равна произведению передаточных функций отдельных звеньев. Это соотношение справедливо лишь в том случае, если выход каждого звена зависит только от его входа и не зависит от выходной координаты последующего звена.

Рисунок 4. Структурная схема соединения звеньев с обратной связью

W _n ( p )

W _ос ( p )

Соединение звеньев с обратной связью. Обратной связью называют передачу сигнала с выхода звена на его вход (рис. 4), где сигнал обратной связи х _ос алгебраически суммируется с внешним сигналом х ( p ) . Причем, если суммарный сигнал x ₁ ( p ) определяется соотношением x ₁ ( p ) = x ( p ) + x _oc ( p ), то обратная связь называется положительной, если x ₁ ( p ) = = x ( p ) – x _oc ( p ), т.е. сигнал обратной связи вычитают из внешнего сигнала, то обратная связь называется отрицательной.

В линии обратной связи в общем случае может быть включено звено, в котором выходной сигнал y ( p ) преобразуется в соответствии с передаточной функцией W _oc ( p ) в сигнал x _oc ( p ). Иногда это звено может отсутствовать, т.е. W _oc ( p ) = l и х_ос ( p ) = у ( p ) .

Найдем соотношение между передаточной функцией замкнутой системы W _зс ( p ) и передаточными функциями отдельных звеньев W _n ( p ) и W _oc ( p ). Уравнения выходных сигналов каждого звена

;

;

.

Исключив из полученной системы уравнений x ₁ ( p ) и x _ос ( p ), получим , или

,

откуда передаточная функция замкнутой системы с положительной обратной связью : ,

передаточная функция замкнутой системы с отрицательной обратной связью: .

В реальных условиях на объект управления оказывают влияние внешние воздействия, которые называют возмущающими. Возмущающие воздействия (возмущения) вызывают отклонение регулируемого параметра от заданного значения.

Возмущения, действующие на САР, представляют собой непрерывные функции времени с различными законами изменения. В этом случае возникают трудности принципиального характера, так как заранее неизвестны законы измерения внешних воздействий, что затрудняет анализ динамики и статики САР. Для ликвидации возникших затруднений часто используют так называемые типовые, управляющие и возмущающие воздействия, которые представляют собой либо наиболее вероятные, либо наиболее неблагоприятные законы изменения управляющих и возмущающих воздействий. Например, довольно широко в качестве типовых используют воздействия полиномиального вида:

,

где n = 0, 1, 2, … – натуральные числа; – постоянные величины; 1 ( t ) – единичная ступенчатая функция,

При n = 0 имеем единичное ступенчатое воздействие: .

При n = 1 получим линейное воздействие: .

На рис. 5 представлены графики единичного ступенчатого и линейного входных воздействий.

Рисунок 5. Типовые полиномиальные воздействия

В некоторых случаях в качестве типового используется единичное импульсное воздействие следующего вида: , где d ( t ) – единичная дельта-функция

Единичная дельта-функция (единичный импульс) представляет собой математическую идеализацию импульса бесконечно малой длительности, бесконечно большой амплитуды, имеющего конечную площадь, равную единицы, т.е. .

Момент приложения внешних воздействий к САР обычно принимается за ноль отсчёта времени. При таком подходе внешние воздействия для отрицательного момента времени равны нулю. В аналитические выражения для внешних воздействий в качестве множителя вводят единичную ступенчатую функцию.

Важнейшей характеристикой САР и её составных элементов являются переходные и импульсные переходные (импульсные) функции. Графическое представление переходных и импульсных функций называют временными характеристиками. Переходной функцией h ( t ) называют функцию, описывающую сигнал на выходе при условии, что на вход подано единичное ступенчатое воздействие, при нулевых начальных условиях. График переходной функции, представляющий собой зависимость функции h ( t ) от времени t , называют переходной характеристикой. В том случае, если амплитуда единичного ступенчатого воздействия отлична от единицы получают разновидность переходной характеристики, которая называется кривой разгона.

Импульсной или весовой функцией w ( t ) называют функцию, описывающую реакцию на единичное импульсное воздействие при нулевых начальных условиях. График зависимости функции w ( t ) от времени называют импульсной переходной (импульсной) характеристикой.

Любое внешнее воздействие сложной формы может быть приближенно представлено в виде совокупности типовых воздействий, связанных между собой определенными математическими операциями.

Аналитическое определение переходных функций и характеристик основано на следующих положениях. Если задана передаточная функция системы или составной части W ( p ) и известен входной сигнал x ( t ), то выходной сигнал y ( t ) определяется следующим соотношением: .

Таким образом, изображение выходного сигнала представляет собой произведение передаточной функции на изображение входного сигнала . Сигнал y ( t ) в явном виде получим после перехода от изображения к оригиналу y ( t ).

Так как изображение единичного ступенчатого воздействия равно , то изображение переходной функции определяется соотношением: . Следовательно, для нахождения переходной функции необходимо передаточную функцию разделить на p и выполнить переход от изображения к оригиналу.

Изображение единичного импульса равно 1. Тогда изображение импульсной функции — . Таким образом, передаточная функция является изображением импульсной функции.

Так как , то между импульсной и переходной функциями существует следующая зависимость: .

Импульсная и переходная функции, как и передаточная функция, являются исчерпывающими характеристиками системы при нулевых начальных условиях. По ним можно определить выходной сигнал при произвольных входных воздействиях.

В работе рассматриваются следующие звенья:

1) идеальное интегрирующее : ;

2) реальное интегрирующее : ;

3) апериодическое 1-го порядка: ;

4) апериодическое 2-го порядка: ;

5) реальное дифференцирующее : ;

6) колебательное ( 0 x ): ;

7) консервативное : ;

8) звено запаздывания: ,

где k – коэффициент пропорциональности (коэффициент усиления); T – постоянная времени интегрирования, с; t – время запаздывания, с; 0 x – коэффициент затухания колебаний (коэффициент демпфирования).

2.2 Алгоритм выполнения работы

1. Записать передаточную функцию звена с нулевыми начальными условиями.

2. Определить вид переходных процессов с учетом единичного ступенчатого и импульсного воздействий.

3. Построить графики переходных процессов при различных значениях постоянных времени и коэффициента усиления. Рассмотреть следующие случаи: — при табличных значениях параметров ( k и T ); — изменив значения коэффициентов усиления с исходными значениями постоянных времени; — изменив значения постоянных времени и исходных значениях коэффициентов усиления.

2.3 Примеры расчета

Для звеньев и соединения звеньев, заданных передаточными функциями: , ,

построить переходные процессы при различных значениях постоянных времени и коэффициента усиления.

1. Передаточная функция реального дифференцирующего звена: , откуда , где – единичное ступенчатое воздействие, или – единичная импульсная функция, следовательно: , .

2. Выполним обратное преобразование Лапласа (табл. 3 прил. 1) и получим переходной процесс для единичного ступенчатого воздействия: . Между импульсной и переходной функциями существует следующая зависимость , то .

3. Строим временные характеристики звена, рис. 6.

Рисунок 6. Временные характеристики реального дифференцирующего звена

4. Передаточная функция апериодического звена второго порядка: , откуда .

Учитывая единичное ступенчатое воздействие или единичную импульсную функцию, получим соответственно:

и

5. Выполним обратное преобразование Лапласа (см. табл. 3 прил. 1) и получим переходной процесс для единичного ступенчатого воздействия .

Импульсная функция .

6. Строим временные характеристики звена (рис. 7).

Рисунок 7. Временные характеристики апериодического звена II -го порядка

7. Передаточная функция для последовательного соединения звеньев . Для последовательно соединенных реального дифференцирующего звена и апериодического звена второго порядка передаточная функция запишется следующим образом:

,

,

где k ₁ – коэффициент усиления; k ₂ – коэффициент усиления апериодического звена второго порядка; T ₁ – постоянная времени реального дифференцирующего звена; T ₂ , T ₃ – постоянные времени апериодического звена второго порядка.

Учитывая единичное ступенчатое воздействие или единичную импульсную функцию, получим соответственно:

,

.

8. Н айдем корни характеристического уравнения методом неопределенных коэффициентов. Получим уравнение вида:

Выполним обратное преобразование Лапласа и получим переходной процесс для единичного ступенчатого воздействия:

9. Строим временные характеристики системы (рис. 8).

Рисунок 8. Временные характеристики системы

2.4 Контрольные вопросы и задания

1. Что такое «типовое звено» САР? Назовите типовые звенья.

2. Что такое передаточная функция САР? Что она характеризует?

3. Основные типы соединения звеньев в структурных схемах.

4. Параллельное соединение звеньев. Структурная схема. Передаточная функция.

5. Последовательное соединение звеньев. Структурная схема. Передаточная функция.

6. Соединение звеньев с обратной связью. Структурная схема. Передаточная функция системы с положительной и отрицательной обратной связью.

7. Что такое «временные характеристики САР»?

8. Что представляет собой переходная функция?

9. Что представляет собой импульсная (весовая) функция?

1. Назовите основные типы возмущающих воздействий САР.

2. Что представляет собой единичная ступенчатая функция?

3. Что представляет собой единичная импульсная функция?

4. Связь между импульсной и переходной функциями.

Видео:Видеометодичка. Практикум по нахождению передаточных функций по дифференциальным уравнениямСкачать

Апериодическое (инерционное, статическое) звено. Передаточная функция и уравнения

Дифференциальное уравнение, описывающее взаимосвязь входного и выходного сигналов апериодического типового динамического звена (ТДЗ), можно представить в следующем виде:

Где: k – коэффициент передачи, Т₀ – постоянная времени.

Дифференциальное уравнение является не самой удобной формой представления математической модели объекта или звена. Это связано с тем, что решения любого дифференциального уравнения довольно сложная вычислительная процедура. Более удобна и, соответственно чаще используемая, математическая модель объекта, записанная в виде передаточной функции.

Передаточная функция – это преобразованное по Лапласу исходное дифференциальное уравнение, то есть уравнение, записанное в виде преобразованных по Лапласу выходного и входного сигналов объекта (звена).

Исходное дифференциальное уравнение в преобразовании Лапласа называют оригиналом, а записанное в операторной форме преобразованное уравнение – его изображением. Суть преобразования Лапласа заключается в замене на функции комплексных переменных Х_вых(р) и Х_вх(р) функций вещественных переменных Х_вых(τ) и Х_вх(τ), где р – оператор Лапласа (комплексное число р = ±m±in). Данные функции связываются между собой интегралом Лапласа:

Для большинства используемых в ТДЗ дифференциальных уравнений, чисто формальным условием перехода от оригинала к изображению будут представленные ниже замены:

Использовав приведенное выше условие довольно легко получить изображение, то есть перейти к операторной форме записи дифференциального уравнения апериодического звена.

Оригинал дифференциального уравнения апериодического звена имеет следующий вид:

Операторная форма записи (изображения) уравнения апериодического звена:

Огромным преимуществом данного преобразования является то, что записанное в операторной форме исходное дифференциальное уравнения становится алгебраическим. Но стоит отметить, что если бы все дифференциальные уравнения можно было бы преобразовать по Лапласу, то в математике произошла бы революция, так как решение алгебраических уравнение значительно проще дифференциальных. К сожалению, такое преобразование возможно лишь для ограниченного количества уравнений, в том числе для уравнений типовых динамических звеньев (ТДЗ).

Поскольку уравнение апериодического звена приняло вид алгебраического, то его можно записать следующим образом:

Из полученного выражения достаточно легко выделить отношение Х_вых(р) / Х_вх(р), которое называется передаточной функцией и для апериодического звена имеет вид:

У каждого типового динамического звена присутствует ряд типовых частотных характеристик: амплитудно-частотную (АЧХ), фазочастотную (ФЧХ), амплитудно-фазовую частотную (АФЧХ или АФХ), логарифмическую амплитудно-частотную (ЛАЧХ), логарифмическую фазочастотную (ЛФЧХ).

На практике чаще всего используется АФЧХ или АФХ.

Амплитудно-фазовая характеристика это вектор, а график АФХ – годограф этого вектора, то есть кривая на комплексной плоскости, которую описывает конец вектора при изменении частоты ω от 0 до ∞. Вектор характеризуется двумя величинами – длина (скаляр или вектор по модулю) и направление (градиент).

Вектор аналитически можно записать в виде двух проекций на действительную и мнимую оси, и выразить эти проекции через угол α:

После использования формулы Эйлера:

Где |W| — длина вектора или вектор по модулю, i – мнимое число:

Аналитическое выражение для любого вектора АФХ любого типичного динамического звена легко получить из передаточной функции, заменив в ней оператор Лапласа р на выражение iω. Где ω – частота колебаний (ω = 2π/Т), Т – период колебаний.

Для апериодического звена амплитудно-фазовая частотная характеристика (АФХ) имеет вид:

Для записи вектора АФХ в виде проекций на действительную и мнимую ось необходимо произвести следующие преобразования:

Изменяя частоту ω от 0 до ∞ можно построить на комплексной плоскости годораф (график вектора АФХ), представляющий из себя полуокружность (рисунок а)), которая располагается в четвертом квадранте комплексной плоскости. Диаметр полуокружности равен коэффициенту k.

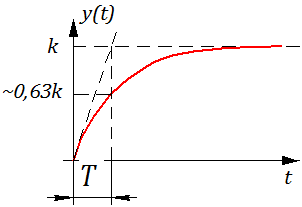
На рисунке б) показана типовая переходная функция апериодического звена. Как видно из графика, она изменяется по экспоненциальному закону. У любой экспоненты есть одно прекрасное свойство – если к любой ее точке провести касательную, а затем точку пересечения касательной с асимптотой и точку касания спроецировать на ось времени, то получится один и тот же отрезок времени на оси времени. Эта проекция, которую называют постоянной времени, соответствует значению коэффициента Т₀ в АФХ и передаточной функции апериодического звена, а ордината асимптоты, к которой стремится экспонента, соответствует коэффициенту k в передаточной функции. Таким образом, по переходной характеристике апериодического звена довольно легко найти коэффициенты Т₀ и k в передаточной функции звена.

Физическим примером апериодического звена может быть конденсатор, при подаче напряжения на который заряд происходит не мгновенно, а с определенной задержкой, или же электродвигатель, который при подаче питания разгоняется не мгновенно, а через какое-то время t. На рисунке в) показан пример установки, которую также можно считать апериодическим звеном (вода – заполняющая бак).

В бак поступает определенное количество воды с расходом Q₁. В то же время из бака вытекает вода с расходом Q₂. Регулируемый параметр в этой системе Х_вых – уровень воды в баке H.

При подаче единичного скачка Q₁ (открыли входной вентиль) уровень воды H в баке повышается. При этом растет гиростатическое давление и возрастает Q₂. Через некоторое время уровень воды H в баке стабилизируется (экспонента приближается к асимптоте). Способность самостоятельно восстанавливать равновесие, которое присуща объектам, аппроксимируемым апериодическим звеном, за счет стока или притока вещества или энергии называют самовыравниванием. Количество самовыравнивания определяет коэффициент р, равный обратному значению коэффициента k в передаточной функции звена, то есть р = 1/k.

В литературе объекты с передаточной функцией апериодического звена называют статическими.

Видео:[ТАУ]Записать передаточную функцию устройства [Составить диф. ур-е для условия передачи напряжения]Скачать

2. Математическое описание систем автоматического управления ч. 2.9 — 2.13

Лекции по курсу «Управление Техническими Системами», читает Козлов Олег Степанович на кафедре «Ядерные реакторы и энергетические установки», факультета «Энергомашиностроения» МГТУ им. Н.Э. Баумана. За что ему огромная благодарность.

Данные лекции только готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется.

В предыдущих сериях:

В это части будут рассмотрены:

2.9. Использование обратных преобразований Лапласа для решения уравнений динамики САР (звена).
2.10. Весовая и переходная функции звена (системы).
2.11. Определение переходного процесса в системе (САР) (звене) через весовую и переходную функции.
2.12. Mетод переменных состояния.
2.13. Переход от описания переменных «вход-выход» к переменным состояния.

Попробуем применить, полученные знания на практике, создавая и сравнивая расчетные модели в разных видах. Будет интересно познавательно и жестко.

2.9. Использование обратных преобразований Лапласа для решения уравнений динамики САР (звена)

Рассмотрим динамическое звено САР изображенное на рисунке 2.9.1

Предположим, что уравнение динамики имеет вид:

где: — постоянные времени;
— коэффициент усиления.

Пусть известны отображения:

Найдем изображения для производных:

Подставим полученные выражения в уравнение динамики и получим уравнение динамики в изображениях:

B(s) — слагаемое, которое определяется начальными условиями, при нулевых начальных условиях B(s)=0.
W(s) — передаточная функция.

Передаточной функцией САР (звена) называется отношение изображений выходного сигнала к входному воздействию при нулевых н.у.

После того, как в явном виде найдено изображение для неизвестной выходной величины, нахождение оригинала не представляет сложностей. Либо по формуле Хэвисайда, либо разложением на элементарные дроби, либо по таблице из справочника.

Пример

Построить выходной сигнал звена САР при единичном входном воздействии и нулевых начальных условиях, если уравнение динамики звена имеет следующий вид:

входное воздействие: — единичное ступенчатое воздействие.

Выполним преобразование Лапласа:

Подставим в уравнение динамики и получим уравнение динамики в изображениях:

Для получения выходного сигнала из уравнения в изображениях выполним обратное преобразования Лапласа:

2.10. Весовая и переходная функции звена (системы).

Определение: Весовой функцией звена (системы) называется реакция системы при нулевых н.у. на единичное импульсное воздействие.

Определение: Переходной функцией звена (системы) при н.у. называется реакция на единичное ступенчатое воздействие.

На этом месте можно вспомнить, что преобразование Лапласа это интеграл от 0 до бесконечности по времени (см. предыдущий текст), а импульсное воздействие при таком интегрировании превращается в 1 тогда в изображениях получаем что:

Передаточная функция играет роль изображения реакции звена или системы на единичное импульсное воздействие.

Для единичного ступенчатого воздействия преобразование Лапласа тоже известно (см. предыдущий текст):

тогда в изображениях получаем, что реакция системы на ступенчатое воздействие, рассчитывается так:

Реакция системы на единичное ступенчатое воздействие рассчитывается обратным преобразованием Лапласа:

2.11. Определение переходного процесса в системе (САР) (звене) через весовую и переходную функции. Формула Дюамеля-Карсона

Предположим, что на вход системы поступает произвольное воздействие x(t), заранее известное. Найти реакцию системы y(t), если известны входное воздействие x(t) и весовая функция w(t).

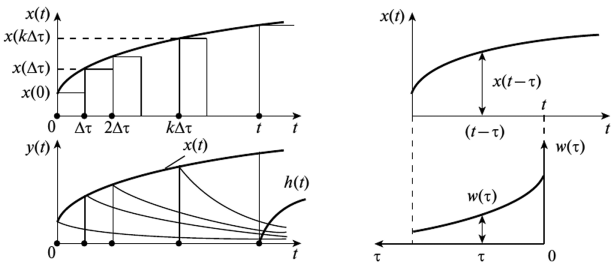
Представим, что входное воздействие представляет собой последовательность прямоугольных импульсов до времени t и ступеньки высотой x(t) в момент времени t. см.рис. 2.11 Для каждого импульса мы можем записать реакцию системы через весовую функциию:

где:
— значение отклика по завершению предыущего импульса;
— время завершения текущего импульса;
— значение весовой функции в начале текущего импульса.

Тогда для определения занчения отклика в произвольный момент времени необходимо сложить все импульсы и ступенчатое воздействие в момент времени t:

Переходя к пределам

если перейти от t к бесконечности мы получим формулу интеграла Дюамеля-Карсона, или по другому «интеграла свертки» который обеспечивает вычисление оригинала функции по произвдению изображения двух функций:

где — вспомогательное время

Для вывода аналогичной зависмости от переходной функции вспомним что изображение весовой и переходной функции связаны соотношением: запишем выражение изображения для отклика в операторной форме:

Используя интеграл свертки получаем, что при известной переходной функции (h(t)) и известному входному воздействию х(t) выходное воздействие рассчитывается как:

2.12. Mетод переменных состояния.

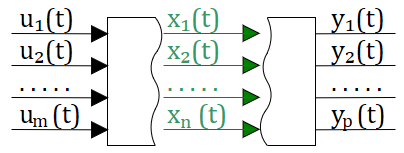
До этого мы рассматривали системы с одной передаточной функцией, но жизнь всегда сложнее и как правило в системах есть несколько передаточных функций несколько входных воздейстий и несколько реакций системы. (см. рис. 2.12.1)

В этом случае наиболее удобной формой пердставления систем для их анализа и расчета оказался метод переменных состояния. Для этого метода, вместо передаточных функций связывающих вход с выходом используются дополнительные переменные состояния, которые описывают систему. В этом случае можно говорить, что состояние системы — это та минимальная информация о прошлом, которая необходима для полного описания будущего поведения (т.е. выходов) системы, если поведение ее входов известно. см. рис. 2.12.2

В методе состояний, производные всех переменных состояния, в общем случае зависит от всех переменных и всех входных воздействия, и могут быть записаны в представленной ниже системы обыкновенных дифференциальных уравнений (ОДУ) первой степени. Эта система уравнений называю системой ОДУ в форме Коши:

Выход из системы зависит от переменных состояния и, в общем случае от входных воздействий и описывается следующей системой уравнений:

где:
n — количество перемнных состояния,
m — количество входных воздействий,
p — количество выходных переменных;

Данная система уравнений может быть записана в матричной форме:

где:
— вектор входа (или вектор управления);
— вектор столбец производных переменных состояния;
— вектор столбец переменных состояния;
— вектор выхода;
— собственная матрица системы [n x n],
— постоянные коэффициенты;
— матрица входа [n x m],
— постоянные коэффициенты;
— матрица выхода а [p x n],
— постоянные коэффициенты;
— матрица обхода [p x m],
— постоянные коэффициенты;

В нашем случае почти всегда все элементы матрицы D будут нулевыми: D = 0.

Такое описание системы позволяет с одной стороны стандартным образом описывать различные технические системы. Явная формула для расчета производных позволяет достаточно просто осуществлять численное интегрирование по времени. И это используется в различных программах моделирования

Другое использование данного представления для простых систем, описанных в переменных «вход-выход», зачастую позволяет устранить технические трудности, связанные с решением ОДУ высокой степени.

Еще одним преимуществом данного описания, является то, что уравнения в форме Коши можно получить из законов физики

Пример решения задачи в форме коши.

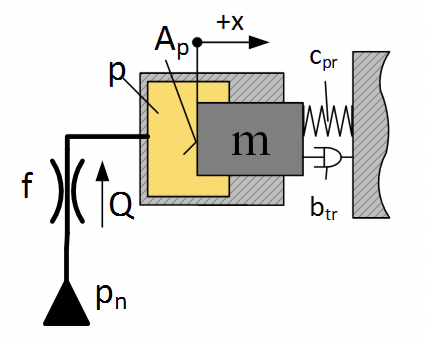
Рассмотрим задачу моделирования гидравлического привода, при следующих условиях:

Дано:
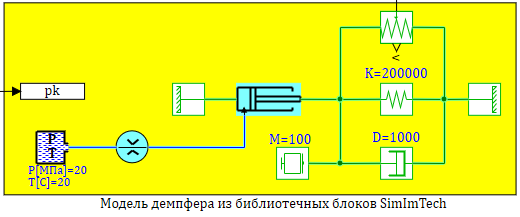
Цилиндрический плунжер диаметром 10 мм, с приведенной массой 100 кг, работает на пружину жесткостью 200 Н/мм и демпфер с коэффициентом вязкого трения — 1000 Н/(м/с). Полость начальным объемом 20 см 3 соединяется с источником давлния дросселем диаметром диаметр которого 0,2 мм. Коэффициент расхода дросселя 0.62. Плотность рабочей жидкости ρ = 850 кг/м 3 .
Определить:
Перемещение дросселя, если в источнике давление происходит скачек 200 бар. см. рис. 2.12.13

Уравенение движение плунжера:

Где: – площадь плунжера, – жесткость пружины, – коэффициент вязкого трения, p – давление в камере.

Поскольку дифференциальное движения это уравнение второго порядка, превратим его в систему из двух уравнений первого порядка, добавив новую переменную — скорость , тогда

Уравнение давления в камере, для упрощения принимаем что изменениям объема камеры из-за перемещения плунжера можно пренебречь:

Где: Q – расход в камеру, V — объем камеры.

Расход через дроссель:

Где: f– площадь дросселя, – давление в источнике, p – давление в камере.
Уравнение дросселя не линейное, по условию задачи, давление входное изменяется скачком, от 0 до 200 бар, проведем линеаризацию в окрестности точки давления 100 бар тогда:

Подставляем линеаризованную формул расхода в формулу давления:

Таким образом общая система уравнений в форме Коши, для рис 2.12.3 привода принимает вид:

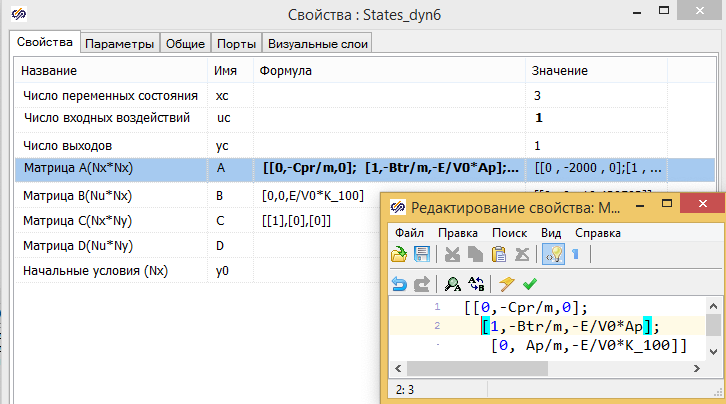
Матрицы A, B, С, В для матричной формы системы уравнений принимают вид:

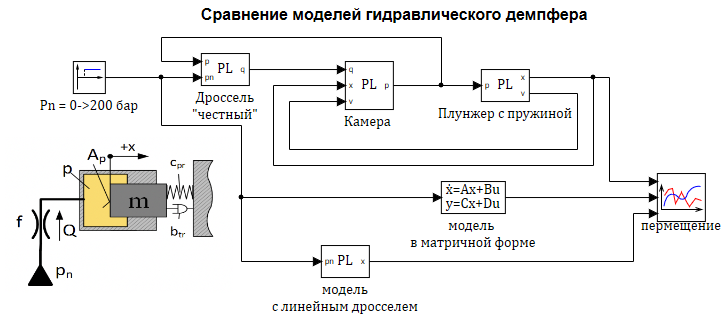
Проверим моделированием в SimInTech составленную модель. На рисунке 2.12.13 представлена расчетная схема содержащая три модели:
1 — «Честная» модель со всеми уравнениями без упрощений.
2 — Модель в блоке «Переменные состояние» (в матричной форме).
3 — Модель в динамическом блоке с линеаризованным дросселем.

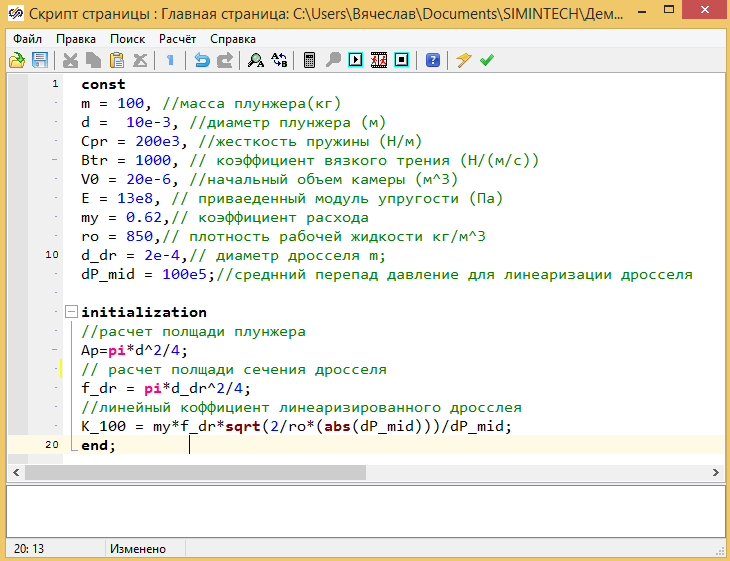
Все условия задачи задаются как глобальные константы проекта, в главном скрипте проекта, там же расчитываются на этапе инициализации расчета, площади плунжера и проходного сечения дросселя см. рис. 2.12.5:

Рисунок 2.12.5 Глобальный скрипт проекта.

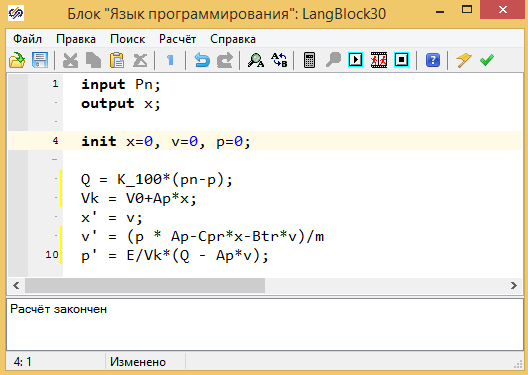
Модель на внутреннем языке программирования представлена на рис. 2.12.6. В данной модели используется описание модели в форме Коши. Так же выполняется учет изменения объема дросселя на каждом шаге расчета, за счет перемещения плунжера (Vk = V0+Ap*x.)

Рисунок 2.12.6 Скрипт расчета модели в форме Коши.

Модель в матричном форме задается с использованием глобальных констант в виде формул. (Матрица в SimInTech задается в виде последовательности из ее столбцов) см. рис. 2.12.7

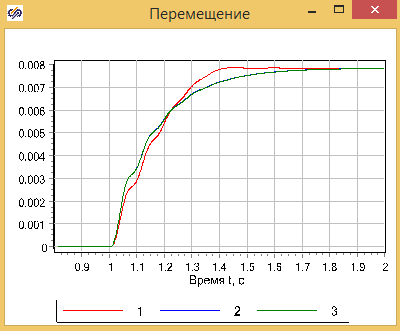
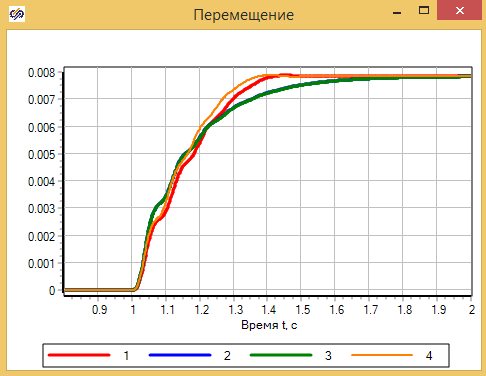
Результаты расчета показывают, что модель в матричной форме и модель на скриптовом языке в форме Коши, практически полностью совпадают, это означает, что учет изменения объема полости практически не влияют на результаты. Кривые 2 и З совпадают.
Процедура линеаризация расхода через дроссель вызывает заметное отличие в результатах. 1-й график c «честной» моделью дросселя, отличается от графиков 2 и 3. (см. рис. 2.12.8)

Сравним полученные модели, с моделью созданной из библиотечных блоков SimInTech, в которых учитываются так же изменение свойств реальной рабочей жидкости — масла АМГ-10. Сама модель представлена на рис. 2.12.9, набор графиков на рисунке 2.12.10

На графиках видно, что уточненная модель отличается от предыдущих, однако погрешность модели составлят наших упрощенных моделей составляют примерно 10%, в лишь в некоторые моменты времени.

2.13. Переход от описания переменных «вход-выход» к переменным состояния и обратно

Рассмотрим несколько вариантов перехода от описания «вход-выход», к переменным состояния:

Вариант прехода зависит от правой части уравнения с переменными «вход-выход»:

2.13.1. Правая часть содержит только b₀*u(t)

В этом варианте, в уравнениях в правой части отсутствуют члены с производными входной величины u(t). Пример с плунжером выше так же относится к этому варианту.

Что бы продемонстрировать технологию перехода рассмотрим следующее уровнение:

Для перехода к форме Коши ведем новые переменные:

И перепишем уравнение относительно y»'(t):

Используя эти переменные можно перейти от дифференциального уравнения 3-го прядка, к системе из 3-х уравнений первого порядка в форме Коши:

Соотвественно матрицы для матричного вида уравнений в переменных сосотяния:

2.13.2. Правая часть общего вида

Более сложный случай, когда в уравнениях есть производные от входных воздействий и уравнение в общем случае выглядит так:

Сделаем преобразования: перейдем к уравнениям динамики в изображениях:

Тогда можно представить уравнение в изображениях в виде:

Разделим уравнение в изображениях на произведение полиномов , получим:

Где: — некоторая комплексная величина (отношение двух комплексных величин). Можно считать, что отображение величины . Тогда входная величина может быть в изображениях представлена как:

Вренемся к оригиналу от изображений получим: ,
где: — дифференциальный оператор.

А это дифференциальное уравнение n-го порядка мы можем преобразовать к системе из n дифференциальных уравнений первого порядка, как это мы делали выше:

Таким образом, мы получили систему уравнение в форе Коши, относительно переменных состояния :

А регулируемую величину (выход системы) мы так же можем выразить через эти переменные, в изображениях:

Перейдем от изображения к оригиналам:

Если обозначить вектор , то мы получим уравнения переменных состояниях в матричной форме, где D = 0:

Пример:

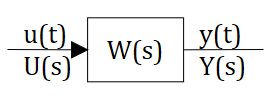
Рисунок 2.13.1 Передаточная функция.

Имеется передаточная функция (рис. 2.13.1) в изображениях :

Необходимо преобразовать передаточную функцию к системе уравнений в форме Коши

В изображения реакция системы связана с входным воздействие соотношением:

Разделим в последнем правую и левую часть на произведения , и введем новую перменную :

Полиномы N(s) и L(s) равны:

Перейдем в последнем выражении от изображения к оригиналам и ведем новые переменные (состояния):

Переходим от уравнения третьего порядка к системе трех уравнений первого порядка:

Или в матричной форме:

Для получения второго матричного уравнения воспользуемся соотношением для новых переменных в отображениях:

Перейдем от изображений к оригиналу:

Таким образом второе уравнение матричной системы выглядит так:

Проверим в SimInTech сравнив передаточную функцию и блок переменных состояния, и убедимся, что графики совпадают см. рис. 2.13.2

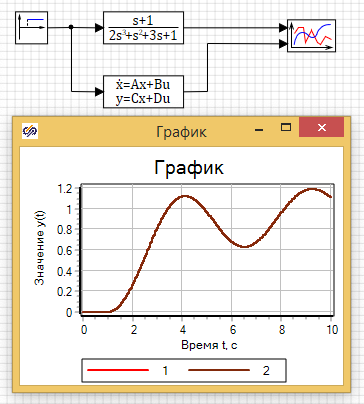
Рисунок 2.13.2 Сравнение переходного процеса у блока передаточной функции и блока переменных состояния.

💥 Видео

7) ТАУ для чайников.Части 3.4 и 3.5 : Передаточная функция. Преобразование Лапласа...Скачать

Метод Лапласа решения ДУСкачать

Передаточные функцииСкачать

proТАУ: 1. Передаточная функцияСкачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Откуда появляются дифференциальные уравнения и как их решатьСкачать

Построить структурную схему САР (САУ) по передаточной функцииСкачать

ТАУ│Передаточная функция устройстваСкачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

c03 7, Динамические звенья 1: передаточная функцияСкачать

Дифференциальные уравнения. 11 класс.Скачать

AGalilov: Преобразование Фурье "на пальцах"Скачать

ТАУ. Matlab/Simulink - моделирование передаточной функции, снятие характеристикСкачать

Преобразование Лапласа - bezbotvyСкачать

Лекция 124. Преобразование Лапласа. ВведениеСкачать

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Дифференциальные уравнения, 1 урок, Дифференциальные уравнения. Основные понятияСкачать