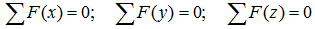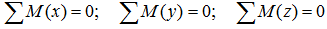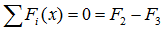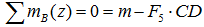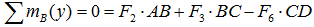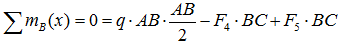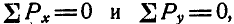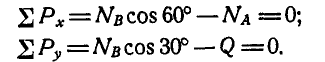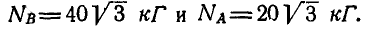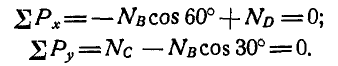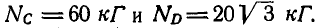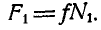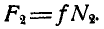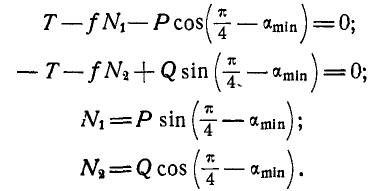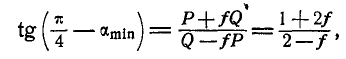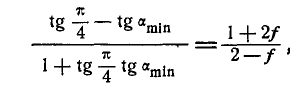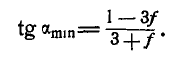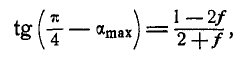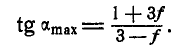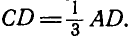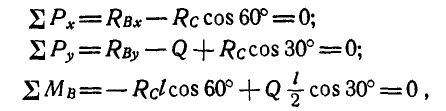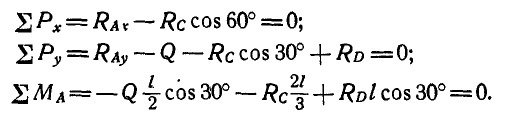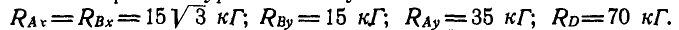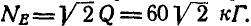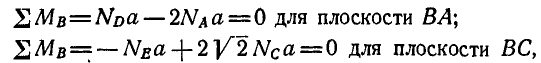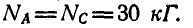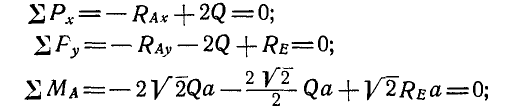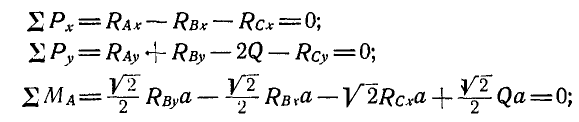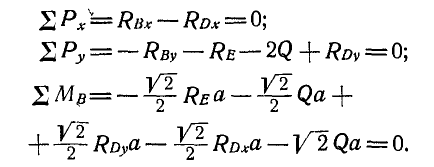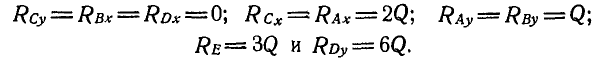Как правильно составлять уравнение равновесия (5 видео)

Условия и уравнения равновесия твердого тела: плоской и пространственной системы сил

Содержание

Условия равновесия произвольной системы сил
Условия равновесия плоской системы сил
Уравнения равновесия для плоской системы сил
Условие равновесия пространственной системы сил
Уравнения равновесия для пространственной системы сил
iSopromat.ru
Пример составления уравнений равновесия
Суммы проекций сил
Суммы моментов
Равновесие системы, состоящей из нескольких тел в теоретической механике
🎦 Видео

Видео:Определение опорных реакций балки. Сопромат для чайников ;)Скачать

Условия равновесия произвольной системы сил

Еще Ньютон говорил, что если геометрическая сумма сил, действующая на тело, равна нулю, то тело:

либо находится в состоянии покоя;
либо движется равномерно прямолинейно.

Из теоретической механики известно, что действие нескольких сил, просуммировав, можно заменить равнодействующей силой:

Тогда обязательное условие равновесия можно записать так:

Однако для полного равновесия, часто, этого условия недостаточно, если тело имеет возможность вращаться относительно какой-то точки или оси, то для равновесия такой системы, необходимо, чтобы выполнялось условие:

где M — главные момент системы, который эквивалентен сумме моментов системы относительно некоторого центра.

Видео:Как выучить Химию с нуля за 10 минут? Принцип Ле-ШательеСкачать

Условия равновесия плоской системы сил

Выше описанные условия означают, что система будет находится в равновесии, когда все силы, действующие на систему, будут взаимно уравновешиваться и момент относительно любой произвольной точки будет равен нулю, отсюда вытекает первая и основная форма условий равновесия для плоской системы сил:

Вторая форма условий равновесия записывается следующим образом:

Важно! Ось не должна быть перпендикулярна прямой AB.

И, наконец, третья форма условий равновесия выглядит так:

Из данной системы уравнений следует, что для равновесия системы достаточно равенства нулю суммы моментов относительно трех точек.

Важно! Точки, относительно которых записываются уравнения не должны лежать на одной прямой.

Видео:Статика. Условия равновесия плоской системы сил (23)Скачать

Уравнения равновесия для плоской системы сил

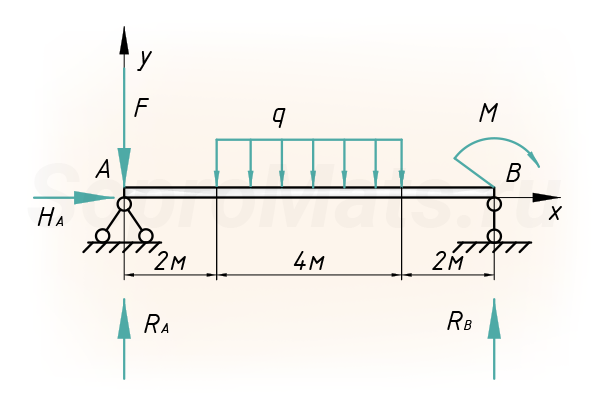
Рассмотрим на примере плоской балки, как записываются уравнения равновесия. Использовать будет классическую (первую) форму условия равновесия:

Сумма моментов относительно точки A:

Сумма проекций всех сил на вертикальную ось (y):

Сумма проекций всех сил на горизонтальную ось(x):

Видео:4.4 Аналитические уравнения равновесияСкачать

Условие равновесия пространственной системы сил

Для пространственной системы сил условие равновесие выглядит вот так:

Таким образом, пространственная система будет находиться в равновесии, если суммы проекций сил на координатные оси, а также суммы моментов относительно осей будут равны нулю.

Видео:Как научиться составлять уравненияСкачать

Уравнения равновесия для пространственной системы сил

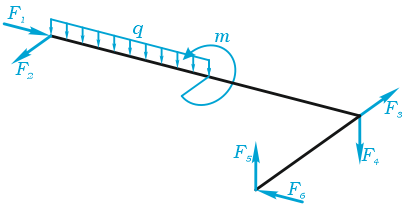
В качестве примера рассмотрим пространственную раму, закруженную сосредоточенными силами. Составим для нее шесть уравнений равновесия:

Видео:Составление уравнений химических реакций. 1 часть. 8 класс.Скачать

iSopromat.ru

Уравнения равновесия (статики) характеризуют неподвижность заданной системы нагруженной комплексом внешних усилий.

При решении задач теоретической механики и сопротивления материалов (например, при определении опорных реакций или внутренних силовых факторов) исходя из условия неподвижности системы или ее частей, записываются уравнения равенства нулю сумм проекций всех сил на оси выбранной системы координат

что следует из условия отсутствия перемещения системы вдоль этих осей, и сумм моментов относительно произвольных точек системы

из условия отсутствия ее вращения относительно указанных осей.

Надо отметить что в случае действия плоской системы сил можно получить только три уравнения статики, а линейная схема нагружения позволяет записать лишь одно уравнение.

Видео:Химические уравнения // Как Составлять Уравнения Реакций // Химия 9 классСкачать

Пример составления уравнений равновесия

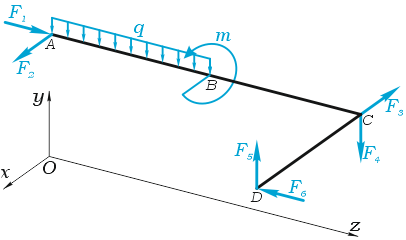
В качестве примера, рассмотрим общий случай пространственного нагружения, где комплекс усилий, включающий сосредоточенные силы F₁-F₆, равномерно распределенную нагрузку q, и момент m расположенный в плоскости перпендикулярной длинному стержню, удерживает L-образную систему в равновесии.

Обозначим характерные точки системы буквами A, B, C и D, зададим положение трехмерной системы координат xyz и запишем уравнения равновесия.

Суммы проекций сил

Сумма проекций всех сил на ось x (с учетом правила знаков для сил):

здесь при записи силы от распределенной нагрузки ее интенсивность q умножается на ее длину AB.

Суммы моментов

Суммы моментов всех нагрузок, например, относительно точки B (с учетом правила знаков для моментов):

в плоскости xOy:
в плоскости xOz:
в плоскости yOz:

Из полученных шести уравнений можно определить не более шести неизвестных усилий.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Видео:Определение реакций опор простой рамыСкачать

Равновесие системы, состоящей из нескольких тел в теоретической механике

Равновесие системы, состоящей из нескольких тел:

До сих пор мы рассматривали равновесие одной материальной точки или одного твердого тела, находящихся под действием сил. При этом мы видели, что для одной точки можно составить два уравнения равновесия

На практике же часто приходится иметь дело с системами, состоящими из нескольких материальных точек или твердых тел, соединенных между собой связями. Примерами таких систем могут служить машины, составленные из отдельных деталей, соединенных определенным образом между собой, сооружения, состоящие из отдельных блоков и пр.

На каждое из таких находящихся в равновесии тел действуют силы, часть которых представляет собой действие остальных тел системы на рассматриваемое и подлежит определению.

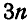
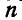
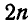
Так как при этом силы, действующие на каждое тело, вообще говоря, не пересекаются в одной точке, то для определения реакций связей в местах соприкасания тел с другими телами системы и связями можно для каждого из тел, входящих в систему, составить 3 уравнения равновесия, а для системы уравнений. Если система, — находящаяся в равновесии, состоит из материальных точек, то число таких уравнений равновесия будет .

Может оказаться при этом, что число неизвестных, подлежащих определению, превысит общее число уравнений равновесия статики, тогда такая задача не может быть решена приемами статики и называется задачей статически неопределимой.

Определение неизвестных реакций связей выясним на отдельных примерах.

Задача №1

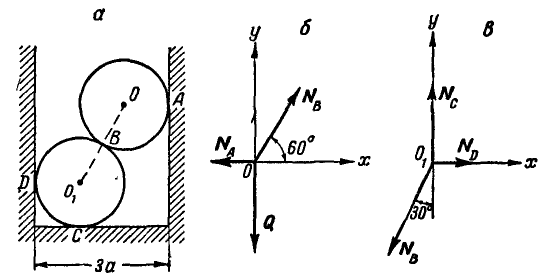
Два одинаковых однородных цилиндра весом Q = 60 кГ каждый (рис. 57, а) соприкасаются между собой в точке В и удерживаются в равновесии двумя вертикальными и горизонтальной плоскостями. Радиус каждого из цилиндров равен а. Пренебрегая трением между цилиндрами и плоскостями, найти реакции 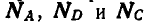в точках A, D и С соприкасания цилиндров и плоскостей.

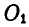
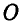
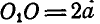
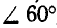
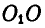
Решение. Соединяя центры цилиндров и прямой, заключаем, что прямая составляет с горизонтальной прямой , так как проекция на горизонталь равна а.

Рассмотрим сначала равновесие верхнего цилиндра (рис. 57, б):.

Отсюда получаем:

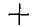
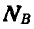
Обе реакции получились, со знаком , следовательно направлением их стрелок мы задались правильно. При рассмотрении равновесия нижнего цилиндра известная уже нам сила по закону «действие равно противодействию» должна быть направлена в противоположную сторону (рис. 57, в):

Отсюда получаем:

Эту задачу можно было бы решить геометрическим способом, построив треугольники равновесия для каждого из цилиндров.

Задача №2

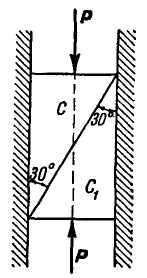
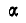
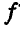
При каком наибольшем и наименьшем угле возможно равновесие грузов Q и Р, расположенных на призме (рис. 59, а), если Q = 2P и коэффициент трения грузов о призму равен ?

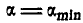
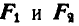
Решение. Рассмотрим сначала предельный случай равновесия грузов Р и Q, когда ; при этом силы трения грузов о плоскость будут направлены в сторону, обратную направлению их возможного движения. Схема сил, действующих на грузы, представлена на рисунке 59, б.

Уравнения равновесия груза Р будут:

, где

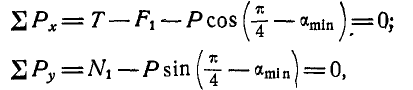
Точно так же уравнения равновесия для груза Q будут:

где

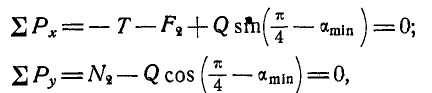
Подставляя вместо 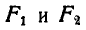и их значения, имеем:

Складывая первые два уравнения и подставляя вместо 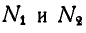их значения, получим:

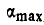
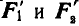
Для нахождения , при котором возможно равновесие грузов, придется силы трения , направить в противоположную сторону (рис. 59, в). Составляя в этом случае, как и в предыдущем, уравнения равновесия для каждого из грузов, получим окончательно:

Задача №3

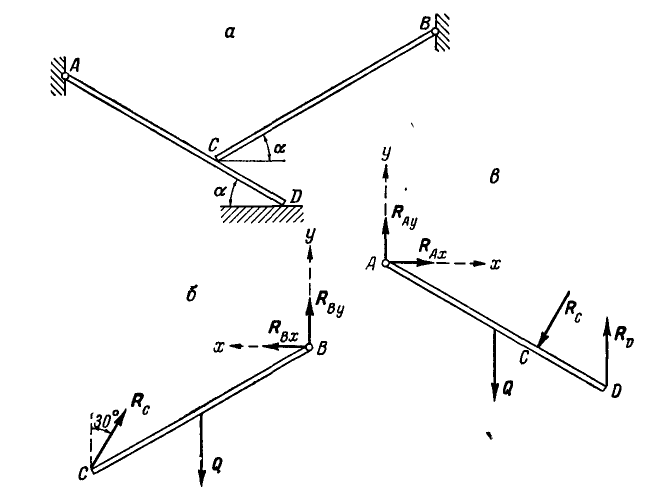
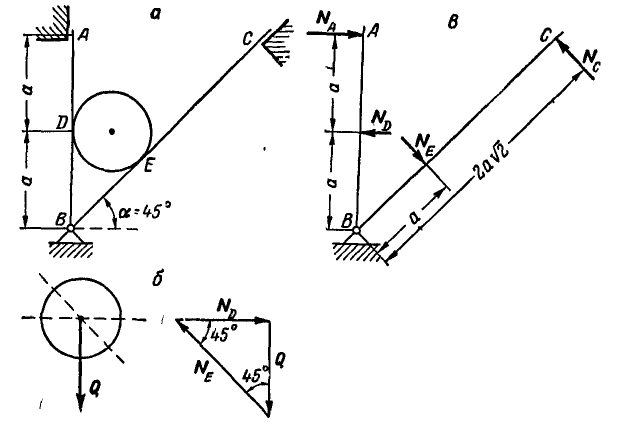
Два однородных бруска AD и СВ одинаковой длины и одинакового веса Q=60 кГ каждый наклонены к горизонтальной прямой под 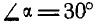(рис. 60, а). В точке С брусок СВ опирается на стержень AD, который, в свою очередь, опирается в точке D на горизонтальную плоскость. Пренебрегая трением, найти реакции в неподвижных шарнирах А и В и в точке D, если

Решение. Рассмотрим равновесие каждого из брусков в отдельности. Составляя сначала уравнения равновесия сил для бруска СВ (рис. 60, б), имеем:

а затем для бруска AD (рис. 60, в):

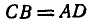
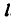
Длина бруска обозначена через .

После решения уравнений получаем:

Задача №4

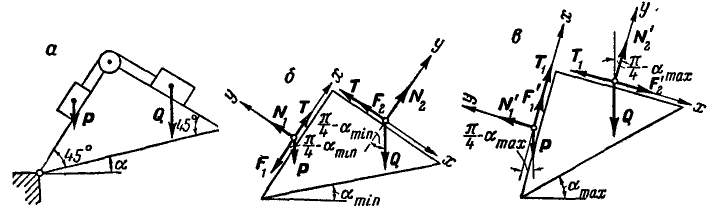
Однородный цилиндр весом Q = 60 кГ опирается свободно на вертикальную и наклонную плоскости АВ и ВС (рис. 61, а). В точках А и С плоскости опираются на гладкие опоры, расположенные на одной горизонтали. Найти давления 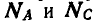в точках А и С, пренебрегая трением цилиндра о плоскости.

Решение. Рассмотрим сначала равновесие цилиндра (рис. 61, б) и, построив для него треугольник равновесия, находим: 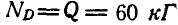и

Теперь уже можно перейти к рассмотрению равновесия плоскостей ВА и ВС (рис. 61, в). Для определения давлений в точках А и С освободимся от связей и взамен них введем реакции 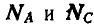. Равновесие каждой из плоскостей, имеющих ось вращения в точке В, будет возможно, если силы, действующие на плоскости, не смогут их вращать, а это будет при условии, если сумма моментов всех сил, приложенных к каждой из плоскостей относительно оси вращения В, равна нулю, т. е.:

откуда

Мы нашли реакции связей в точках А и С; давления же в этих точках, численно равные реакциям связей, будут направлены в противоположные реакциям 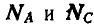стороны.

Задача №5

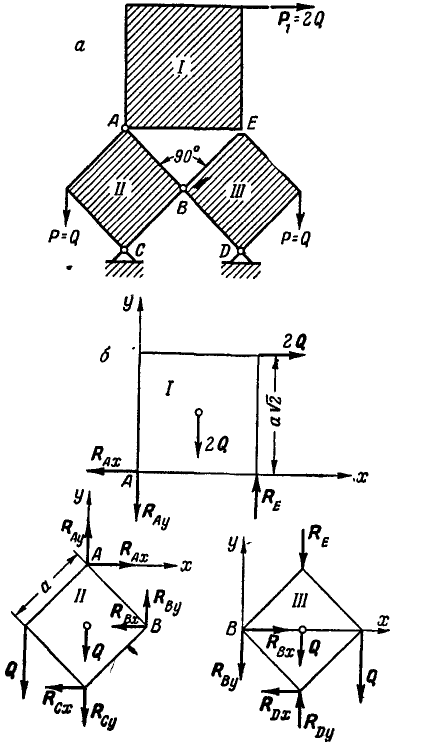
Система состоит из трек однородных квадратных пластинок I, II и III, соединенных в точках А, В, С и D шарнирно (рис. 62, а). Вес каждой из пластинок II и III равен Q кГ. Зная, что веса пластинок пропорциональны их площадям, найти реакции связей в шарнирах С и D, пренебрегая трением.

Решение. Общее число неизвестных сил равно девяти, так как каждый из неподвижных шарниров А, В, С и D дает по две неизвестные составляющие реактивные силы, а девятая реактивная сила, известная по направлению, возникает в точке Е, Для определения девяти неизвестных необходимо иметь девять уравнений, которые мы получим, если рассмотрим в отдельности равновесие каждой из пластинок I, II и III (рис. 62, б).

На чертеже указано направление действующих на каждую из пластинок сил.

Составляя для каждой из пластинок по три уравнения равновесия, имеем:

для пластинки

Решая полученные девять уравнений с девятью неизвестными, находим:

Все модули реакций получились со знаком плюс. Если бы некоторые из найденных модулей получились со знаком минус, то направление стрелок соответствующих реакций пришлось бы изменить на обратное тому, которое было принято при решении задачи.

Рекомендую подробно изучить предмет:

Теоретическая механика

Ещё лекции с примерами решения и объяснением:

Графостатика в теоретической механике
Расчет ферм
Пространственная система сходящихся сил
Момент силы относительно точки и относительно оси
Векторное исчисление
Виды связей
Параллельные силы
Произвольная плоская система сил

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.