Как построить уравнение регрессии в r studio

Статистика в последнее время получила мощную PR поддержку со стороны более новых и шумных дисциплин — Машинного Обучения и Больших Данных. Тем, кто стремится оседлать эту волну необходимо подружится с уравнениями регрессии. Желательно при этом не только усвоить 2-3 приемчика и сдать экзамен, а уметь решать проблемы из повседневной жизни: найти зависимость между переменными, а в идеале — уметь отличить сигнал от шума.

Для этой цели мы будем использовать язык программирования и среду разработки R, который как нельзя лучше приспособлен к таким задачам. Заодно, проверим от чего зависят рейтинг Хабрапоста на статистике собственных статей.

Видео:Построение регрессионных моделей в R. Оценка точности и адекватности моделейСкачать

Введение в регрессионный анализ

Если имеется корреляционная зависимость между переменными y и x , возникает необходимость определить функциональную связь между двумя величинами. Зависимость среднего значения называется регрессией y по x .

Основу регрессионного анализа составляет метод наименьших квадратов (МНК), в соответствии с которым в качестве уравнения регресии берется функция такая, что сумма квадратов разностей минимальна.

Карл Гаусс открыл, или точнее воссоздал, МНК в возрасте 18 лет, однако впервые результаты были опубликованы Лежандром в 1805 г. По непроверенным данным метод был известен еще в древнем Китае, откуда он перекочевал в Японию и только затем попал в Европу. Европейцы не стали делать из этого секрета и успешно запустили в производство, обнаружив с его помощью траекторию карликовой планеты Церес в 1801 г.

Вид функции , как правило, определен заранее, а с помощью МНК подбираются оптимальные значения неизвестных параметров. Метрикой рассеяния значений вокруг регрессии является дисперсия.

• k — число коэффициентов в системе уравнений регрессии.

Чаще всего используется модель линейной регрессии, а все нелинейные зависимости приводят к линейному виду с помощью алгебраических ухищрений, различных преобразования переменных y и x .

Линейная регрессия

Уравнения линейной регрессии можно записать в виде

В матричном виде это выгладит

• y — зависимая переменная;
• x — независимая переменная;
• β — коэффициенты, которые необходимо найти с помощью МНК;
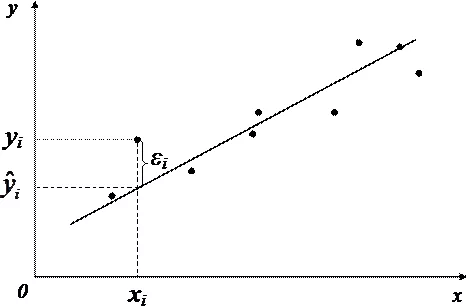
• ε — погрешность, необъяснимая ошибка и отклонение от линейной зависимости;

Случайная величина может быть интерпретирована как сумма из двух слагаемых:

• — полная дисперсия (TSS).
• — объясненная часть дисперсии (ESS).
• — остаточная часть дисперсии (RSS).

Еще одно ключевое понятие — коэффициент корреляции R 2 .

Видео:Линейная регрессия на RСкачать

Ограничения линейной регрессии

Для того, чтобы использовать модель линейной регрессии необходимы некоторые допущения относительно распределения и свойств переменных.

1. Линейность, собственно. Увеличение, или уменьшение вектора независимых переменных в k раз, приводит к изменению зависимой переменной также в k раз.
2. Матрица коэффициентов обладает полным рангом, то есть векторы независимых переменных линейно независимы.
3. Экзогенность независимых переменных — . Это требование означает, что математическое ожидание погрешности никоим образом нельзя объяснить с помощью независимых переменных.
4. Однородность дисперсии и отсутствие автокорреляции. Каждая ε_i обладает одинаковой и конечной дисперсией σ 2 и не коррелирует с другой ε_i. Это ощутимо ограничивает применимость модели линейной регрессии, необходимо удостовериться в том, что условия соблюдены, иначе обнаруженная взаимосвязь переменных будет неверно интерпретирована.

Как обнаружить, что перечисленные выше условия не соблюдены? Ну, во первых довольно часто это видно невооруженным глазом на графике.

Неоднородность дисперсии

При возрастании дисперсии с ростом независимой переменной имеем график в форме воронки.

Нелинейную регрессии в некоторых случая также модно увидеть на графике довольно наглядно.

Тем не менее есть и вполне строгие формальные способы определить соблюдены ли условия линейной регрессии, или нарушены.

• Автокорреляция проверяется статистикой Дарбина-Уотсона (0 ≤ d ≤ 4). Если автокорреляции нет, то значения критерия d≈2, при позитивной автокорреляции d≈0, при отрицательной — d≈4.
• Неоднородность дисперсии — Тест Уайта, , при chi_$» data-tex=»inline»/> нулевая гипотеза отвергается и констатируется наличие неоднородной дисперсии. Используя ту же можно еще применить тест Бройша-Пагана.
• Мультиколлинеарность — нарушения условия об отсутствии взаимной линейной зависимости между независимыми переменными. Для проверки часто используют VIF-ы (Variance Inflation Factor).

В этой формуле — коэффициент взаимной детерминации между и остальными факторами. Если хотя бы один из VIF-ов > 10, вполне резонно предположить наличие мультиколлинеарности.

Почему нам так важно соблюдение всех выше перечисленных условий? Все дело в Теореме Гаусса-Маркова, согласно которой оценка МНК является точной и эффективной лишь при соблюдении этих ограничений.

Видео:Как посчитать регрессию в R. Интерпретация коэффициентов регрессииСкачать

Как преодолеть эти ограничения

Нарушения одной или нескольких ограничений еще не приговор.

1. Нелинейность регрессии может быть преодолена преобразованием переменных, например через функцию натурального логарифма ln .
2. Таким же способом возможно решить проблему неоднородной дисперсии, с помощью ln , или sqrt преобразований зависимой переменной, либо же используя взвешенный МНК.
3. Для устранения проблемы мультиколлинеарности применяется метод исключения переменных. Суть его в том, что высоко коррелированные объясняющие переменные устраняются из регрессии, и она заново оценивается. Критерием отбора переменных, подлежащих исключению, является коэффициент корреляции. Есть еще один способ решения данной проблемы, который заключается в замене переменных, которым присуща мультиколлинеарность, их линейной комбинацией. Этим весь список не исчерпывается, есть еще пошаговая регрессия и другие методы.

К сожалению, не все нарушения условий и дефекты линейной регрессии можно устранить с помощью натурального логарифма. Если имеет место автокорреляция возмущений к примеру, то лучше отступить на шаг назад и построить новую и лучшую модель.

Видео:Эконометрика. Линейная парная регрессияСкачать

Линейная регрессия плюсов на Хабре

Итак, довольно теоретического багажа и можно строить саму модель.
Мне давно было любопытно от чего зависит та самая зелененькая цифра, что указывает на рейтинг поста на Хабре. Собрав всю доступную статистику собственных постов, я решил прогнать ее через модель линейно регрессии.

Загружает данные из tsv файла.

• points — Рейтинг статьи
• reads — Число просмотров.
• comm — Число комментариев.
• faves — Добавлено в закладки.
• fb — Поделились в социальных сетях (fb + vk).
• bytes — Длина в байтах.

Вопреки моим ожиданиям наибольшая отдача не от количества просмотров статьи, а от комментариев и публикаций в социальных сетях. Я также полагал, что число просмотров и комментариев будет иметь более сильную корреляцию, однако зависимость вполне умеренная — нет надобности исключать ни одну из независимых переменных.

Теперь собственно сама модель, используем функцию lm .

В первой строке мы задаем параметры линейной регрессии. Строка points

. определяет зависимую переменную points и все остальные переменные в качестве регрессоров. Можно определить одну единственную независимую переменную через points

reads , набор переменных — points

Перейдем теперь к расшифровке полученных результатов.

• Intercept — Если у нас модель представлена в виде , то тогда — точка пересечения прямой с осью координат, или intercept .
• R-squared — Коэффициент детерминации указывает насколько тесной является связь между факторами регрессии и зависимой переменной, это соотношение объясненных сумм квадратов возмущений, к необъясненным. Чем ближе к 1, тем ярче выражена зависимость.
• Adjusted R-squared — Проблема с в том, что он по любому растет с числом факторов, поэтому высокое значение данного коэффициента может быть обманчивым, когда в модели присутствует множество факторов. Для того, чтобы изъять из коэффициента корреляции данное свойство был придуман скорректированный коэффициент детерминации .
• F-statistic — Используется для оценки значимости модели регрессии в целом, является соотношением объяснимой дисперсии, к необъяснимой. Если модель линейной регрессии построена удачно, то она объясняет значительную часть дисперсии, оставляя в знаменателе малую часть. Чем больше значение параметра — тем лучше.
• t value — Критерий, основанный на t распределении Стьюдента . Значение параметра в линейной регрессии указывает на значимость фактора, принято считать, что при t > 2 фактор является значимым для модели.
• p value — Это вероятность истинности нуль гипотезы, которая гласит, что независимые переменные не объясняют динамику зависимой переменной. Если значение p value ниже порогового уровня (.05 или .01 для самых взыскательных), то нуль гипотеза ложная. Чем ниже — тем лучше.

Можно попытаться несколько улучшить модель, сглаживая нелинейные факторы: комментарии и посты в социальных сетях. Заменим значения переменных fb и comm их степенями.

Проверим значения параметров линейной регрессии.

Как видим в целом отзывчивость модели возросла, параметры подтянулись и стали более шелковистыми , F-статистика выросла, так же как и скорректированный коэффициент детерминации .

Проверим, соблюдены ли условия применимости модели линейной регрессии? Тест Дарбина-Уотсона проверяет наличие автокорреляции возмущений.

И напоследок проверка неоднородности дисперсии с помощью теста Бройша-Пагана.

Видео:Множественный регрессионный анализ в R (multiple regression in R)Скачать

В заключение

Конечно наша модель линейной регрессии рейтинга Хабра-топиков получилось не самой удачной. Нам удалось объяснить не более, чем половину вариативности данных. Факторы надо чинить, чтобы избавляться от неоднородной дисперсии, с автокорреляцией тоже непонятно. Вообще данных маловато для сколь-нибудь серьезной оценки.

Но с другой стороны, это и хорошо. Иначе любой наспех написанный тролль-пост на Хабре автоматически набирал бы высокий рейтинг, а это к счастью не так.

Видео:Нелинейная регрессия в MS Excel. Как подобрать уравнение регрессии? Некорректное значение R^2Скачать

17 Линейная регрессия

Вы уже умеете считать коэффициент корреляции Пирсона:

Простая линейная регрессия — это примерно то же самое. В синтаксисе линейной регрессии уже не обойтись без формул, это такой специальный тип данных в R:

Если видите эту волнистую линию — тильду (

), это значит, что перед вами формула. Мы уже сталкивались с формулами ранее, они иногда используются для задания отношений между переменными, например, для определения фасеток на графике (@ref(gg_base)).

Давайте исследуем зависимость размера рюкзака от массы тела. В простой линейной регрессии, в отличие от корреляции, есть направленность: одна переменная является как бы независимой переменной или предиктором, другая — как бы объясняемой переменной (outcome). В формуле предикторы находятся справа от тильды, а объясняемая переменная — слева.

Я специально написал “как бы”: если одна переменная предиктор, а другая объясняется этим предиктором, то кажется, что они должны быть обязательно связаны причинно-следственной связью. Это не так: обозначения условны, более того, вы можете поменять переменные местами и ничего не изменится! Короче говоря, линейная регрессия не дает никакой магической каузальной силы исследуемым переменным.

Видео:Проверка гипотез о коэффициентах в RСкачать

17.1 Функция lm()

Давайте посчитаем линейную регрессию функцией lm() .

print(model) или просто model выводит коэфициенты линейной регрессии — это коэффициенты прямой, которая лучше всего подогнанна к данным. Как измеряется качество этой подгонки? В расстоянии точек исходных точек до прямой. По идее, расстояние до прямой нужно было бы считать просто по модулю. И так делают, хоть и очень редко. Обычно в линейной регрессии используются квадратичные расстояния точек до прямой для оценки расстояния (метод наименьших квадратов — ordinary least squares). Это дает кучу клевых математических свойств, например, возможность легко аналитически найти коэффициенты прямой линейной регрессии.

Давайте теперь нарисуем регрессионную прямую поверх диаграммы рассеяния:

Функция predict() позволяет скормить модели новые данные и получить предсказания для новых значений предикторов. Попробуем поиграть с этим немного. Допустим, предскажем вес рюкзака для студента весом в 100 кг:

Мы можем даже попробовать какие-нибудь экстремальные значения для предикторов. Например, сколько будет весить рюкзак студента весом 1000 кг?

Очевидно, что в этом не очень много смысла: студент весом 1000 кг не сможет ходить на занятия, поэтому и про вес рюкзака как-то не имеет смысл спрашивать. Это проблема экстрополяции: линейная регрессия позволяет более-менее достоверно предсказывать значения внутри диапазона значений, на которых была построена модель. Еще один “странный” пример — студент весом 0 кг.

Здесь бессмысленность происходящего еще очевиднее. Конечно, вес студента не может быть равен нулю, иначе это не студент вовсе. Однако это позволяет понять, что такое intercept модели — это значение зависимой переменой в случае, если предиктор равен нулю. А коэффициент предиктора означает, насколько килограммов увеличивается вес рюкзака при увеличении веса студента на 1 кг: на 0.0371297. Не очень много!

Видео:Логистическая регрессия в R (logistic regression in R)Скачать

17.2 Интерпретация вывода линейной регрессии

Гораздо более подробные результаты мы получим, если применим уже известную нам generic функцию summary() на нашу модель.

Теперь мы понимаем, что это за коэффициенты. Однако это всего лишь их оценка. Это значит, что мы допускаем, что в реальности есть некие настоящие коэффициенты линейной регрессии, а каждый раз собирая новые данные, они будут посчитаны как немного разные. Короче говоря, эти коэффициенты — те же статистики, со своим выборочным распределением и стандартными ошибками. На основе чего и высчитывается p-value для каждого коэффициента — вероятность получить такой и более отклоняющийся от нуля коэффициент при верности нулевой гипотезы — независимости зависимой переменной от предиктора.

Кроме p-value, у линейной регрессии есть (R^2) — доля объясненной дисперсии. Как ее посчитать? Для начала давайте сохраним как отдельные колонки ошибки (необъясненную часть модели) и предсказанные значения (они означают объясненную часть модели). Можно убедиться, что сумма предсказанных значений и ошибок будет равна зависимой переменной.

Соответственно, вся сумма объясненной дисперсии разделяется на объясненую и необъясненную. Полная дисперсия (total sum of squares = TSS) может быть посчитана как сумма квадратов разниц со средним. Необъясненная дисперсия — это сумма квадратов ошибок — residual sum of squares (RSS).

Это очень мало, мы объяснили всего 3.5846285% дисперсии. Собственно, и p-value больше, чем 0.05.

При этом p-value тот же, что и при коэффициенте корреляции Пирсона. Это не случайно: (R^2) — это квадрат коэффициента корреляции Пирсона, если речь идет только об одном предикторе. Давайте это проверим:

Видео:Как вычислить линейный коэффициент корреляции в MS Excel и построить уравнение регрессии?Скачать

17.3 Допущения линейной регрессии

Как и в случае с другими параметрическими методами, линейная регрессия имеет определенные допущения относительно используемых данных. Если они не соблюдаются, то все наши расчеты уровня значимости могут некорректными.

Очень важно ставить вопрос о том, насколько результаты будут некорректными. Как сильно нарушения допущений будет влиять на модель? Ответ на этот вопрос может быть контринтуитивен. Например, достаточно большие отклонения от нормальности нам обычно не страшны при условии того, что выборка достаточно большая.

Допущения линейной регрессии связаны с ошибками: они должны быть нормально распределены, а разброс ошибок должен не уменьшаться и не увеличиваться в зависимости от предсказанных значений. Это то, что называется гомоскедастичностью или гомогенностью (когда все хорошо) и гетероскедастичностью или гетерогенностью (когда все плохо).

Если мы применим функцию plot() , то получим 4 скаттерплота:

Зависимость ошибок от предсказанных значений. На что здесь смотреть? На симметричность относительно нижней и верхней части графика, на то, что разброс примерно одинаковый слева и справа.

Q-Q plot. Здесь все довольно просто: если ошибки являются выборкой из нормального распределения, то они выстраиваются в прямую линию. Если это мало похоже на прямую линию, то имеет место отклонение от нормальности.

Scale-Location plot. Этот график очень похож на график 1, только по оси у используются квадратные корни модуля ошибки. Еще один способ исследовать гетеро(гомо)скедастичность и находить выбросы.

Residuals-Leverage plot. Здесь по оси х — расстояние Кука, а по оси у — стандартизированный размер выбросов. Расстояние Кука показывает high-leverage points — точки, которые имеют экстремальные предсказанные значения, то есть очень большие или очень маленькие значения по предикторам. Для линейной регрессии такие значения имеют большее значение, чем экстремальные точки по предсказываемой переменной. Особенно сильное влияние имеют точки, которые имеют экстремальные значения и по предикторам, и по предсказываемой переменной. Одна такая точка может поменять направление регрессионной прямой! Расстояние Кука отражает уровень leverage, а стандартизированные ошибки отражают экстремальные значения по у (вернее, экстремальные отклонения от предсказанных значений). В этом графике нужно смотреть на точки с правой стороны графика, особенно если они находятся высоко или низко по оси у.

Видео:Уравнение линейной регрессии. Интерпретация стандартной табличкиСкачать

17.4 Влияние выбросов на линейную модель

Давайте теперь попробуем посмотреть, как изменится модель, если выкинуть high leverage points (экстремальные значения по предиктору — body) и что будет, если выкинуть экстремальные значения по у. Обычная линия — регрессионная прямая для модели со всеми точками, штрихованная линия — регрессионная прямая для модели без экстремальных значений по предиктору, пунктирная линия — регрессионная прямая для модели без экстремальных значений по предсказываемой переменной.

Таким образом, именно экстремальные значения по предиктору, а не по объяснияемой переменной имеют особенно сильное значение на регрессионную модель.

Видео:Математика #1 | Корреляция и регрессияСкачать

17.5 Множественная линейная регрессия

В множественной линейной регрессионной регрессии у нас появляется несколько предикторов. Какая модель лучше: где есть много предикторов или где мало предикторов? С одной стороны, чем больше предикторов, тем лучше: каждый новый предиктор может объяснить чуть больше необъясненной дисперсиии. С другой стороны, если эта прибавка маленькая (а она всегда будет не меньше нуля), то, возможно, новый предиктор просто объясняет “случайный шум.” В действительности, если у нас будет достаточно много предикторов, то мы сможем объяснить любые данные! Парадоксальным образом такая модель будет давать очень хорошие результаты на той выборке, по которой мы считаем коэффициенты, но делать очень плохие предсказания на новой выборке — это то, что в машинном обучении называют переобучением (overfitting). Идеальная модель будет включать минимум предикторов, которые лучше всего объясненяют исследуемую переменную. Это что-то вроде бритвы Оккама в статистике.

Поэтому часто используются показатели качества модели, которые “наказывают” модель за большое количество предикторов. Например, adjusted R 2 :

Здесь n — это количество наблюдений, p — количество параметров.

Итак, добавим новый предиктор — Units. Это количество кредитов, которые студенты взяли в четверти 41 . Можно предположить, что чем больше у студента набрано кредитов, тем более тяжелый у нее/него рюкзак. Давайте добавим это как второй предиктор. Для этого нужно просто записать второй предиктор в формуле через плюс.

Множественная линейная регрессия имеет еще одно допущение: отсутствие мультиколлинеарности. Это значит, что предикторы не должны коррелировать друг с другом.

Для измерения мультколлинеарности существует variance inflation factor (VIF-фактор). Считается он просто: для предиктора (i) считается линейная регрессия, где все остальные предикторы предсказывают предиктор (i) .

Сам VIF-фактор считается на основе полученного R 2 регрессии:

Если R_i 2 большой, то и VIF_i выходит большим. Это означает, что предиктор сам по себе хорошо объясняется другими предикторами. Какой VIF считать большим? Здесь нет единого мнения, но если он выше 3 и особенно если он выше 10, то с этим нужно что-то делать.

В нашем случае это не так. Но если бы VIF был большим для какого-либо предиктора, то можно было бы либо попробовать его выкинуть или же использовать анализ главных компонент (см. 21.2), о котором пойдет речь в один из следующих дней.

ANOVA от ANalysis Of VAriance, по-русски часто читается как “АНОВА.”↩︎

Видео:Регрессия - как строить и интерпретировать. Примеры линейной и множественной регрессии.Скачать

Введение в R: часть 3

Pavel Polishchuk, 2014

Примеры построения моделей в R.

1. Линейная регрессия (lm)
2. Метод частичных наименьших квадратов (pls)
3. Метод Random Forest (randomForest)
4. Пример решения классификационной задачи методом Random Forest

Видео:Парная регрессия: линейная зависимостьСкачать

Линейная регрессия (lm)

Построение моделей

Сгенерируем набор данных для моделирования в соответствии с формулой
[ Y = x_1 + x_2^2 + x_1 times x_2 + noise ]

Для этого вначале инициализируем генератор случайных чисел, чтобы получать всегда воспроизводимый результат при генерации случайных чисел.

Сгенерируем случайные переменные ( x_1 ) и ( x_2 ) в соответствии с законом нормального распределения

Сгенерируем зависимую переменную в соответствии с вышеприведенной формулой

Объединим эти параметры в одном data.frame

Рассмотрим созданный набор данных. Построим гистограмму распределению значений Y и посмотрим как рапределены значения переменных между собой попарно.

Посчитаем матрицу взаимных корреляций всех переменных между собой и округлим результат до двух цифр после запятой

Помимо традиционного коэффицента корреляции Пирсона функцией cor можно посчитать ранговый коэффицент корреляции Спирмена.

И из рисунка и из таблиц видно, что связь между ( y ) и ( x_2 ) довольно тесная.

Альтернативный способ представления данных — использование функции pairs.panels пакета psych , которая возвращает одновременно и диаграммы распределения данных и значения коэффициентов корреляции.

Зададим индексы для объектов обучающей и тестовой выборки

Построим несколько моделей в соответствии с различными формулами, которые определяют вид искомой зависимости.

Попробуем сперва обычную линейную комбинацию исходных переменных.

В результате мы получили уравнение вида [ Y = 3.377pm0.625*x_1 + 8,567pm0,415*x_2 — 6,379pm3,493 ]
Все коэффициенты в уравнении статистически значимы с высоким уронеем достоверности, кроме свободного члена, который имеет низкий уровень статистической достоверности. Величина ( R^2 = 0.818 ) является статистически достоверной.

Коэффициент детерминации

Скорректированный коэффициент детерминации с использованием несмещенных оценок

( y_i ) — наблюдаемое значение ( y )
( hat_i ) — предсказанное по модели значение ( y )
( bar ) — среднее значение наблюдаемых значений ( y )
( n ) — количество наблюдений
( k ) — количество параметров

Применим одну из простейших процедур отбора переменных — исключим незначащие члены из уравнения

Коэффициент детерминации существенно увеличился ( R^2 = 0.914 )

Сравнение моделей

Определим с помощью дисперсионного анализа является ли отличие моделей значимым или нет.

Величина 0.071 > 0.05, поэтому можно утверждать, что с вероятностью 95% отличие моделей не значимо и мы в праве выбрать любую модель.

Попытаемся построить более сложные модели.

Модель учитывающее произведение независимых переменных

Модель второго порядка, учитывающая квадраты независимых переменных

В последнем случае видно, что все коэффициенты в уравнении имеют высокую значимость и коэффициент детерминации также высокий ( R^2 = 0.958 )

Сравнение моделей указывает на значимое отличие последней модели от предыдущей.

Для сравнения построим модель с использованием правильной функциональной зависимости

Свободный членя является не значимым, следовательно зависимость проходит через начало отсчета. Построим модель без свободного члена.

Прогноз значений для тестового набора данных

Сопоставим качество прогноза с истинным значением ( y )

Визуализация моделей

Зададим вид вывода результатов и применим функцию plot к моделям m4 и m6 .

Вернем вид вывода результатов к виду по умолчанию

Видео:Корреляционно-регрессионный анализ многомерных данных в ExcelСкачать

Метод частичных наименьших квадратов (pls)

Воспользуемся функцией summary для вывода статистики модели

Чтобы посчитать коэффициент детерминации для обучающей выборки и для случая кросс-валидации воспользуемся следующими функциями. Следует отметить, что модель pls в качестве прогнозированных значений возвращает массив!

Для pls модель также возможно использовать функцию plot , которая возвращает диаграмму зависимости предсказанных значений от наблюдаемых

Спрогнозируем значения тестовой выборки и оценим качество прогноза

Используем другой вид зависимости, который был успешно применен ранее в случае линейной регрессии

Как видно качество модели значительно уеличилось. Подтвердим это оценив прогнозирующую способность модели на тестовом наборе данных.

Видео:Регрессия. Регрессионный анализ в ExcelСкачать

Метод Random Forest (randomForest)

Следует отметить, что большинство функций имеют несколько способов вызова через определение функции как в вышеприведенном случае, либо через указание матрицы X и вектора Y. Так построение модели можно осуществить через
rf.m

Вызовем статистику модели

Рассчитаем значения коэффициента детерминации для out-of-bag выборки (внутренняя валидация моделей)

Функция plot в случае моделей случайного леса возвращает зависимость величины среднеквадратичной ошибки прогноза out-of-bag выборки от количества деревьев в лесе

Чтобы оценить качество модели предскажем тестовый набор данных

Построим график зависимости между предсказанными и наблюдаемыми значениями

Видео:LASSO регрессия в RСкачать

Решение классификационных задач методом Random Forest

Конвертируем значения y из df в два класса по заданному граничному значению

Построение классификационной модели ничем не отличается от регресссионных моделей. Алгоритм сам выбирает тип модели (скласссификационная или регрессионная) в зависимости от типа данных передаваемого Y. Если Y представлен числовыми значениями, то по умолчанию будет построена регрессионная модель, если Y представлен как factor, то будет построена классификационная модель.

Обратите внимание на способ представления формулы. Знак минус указывает, что эти переменные должны быть исключены из расммотрения при построении модели.

Выведем статистику модели

Проверим прогнозирующую способность на тестовом наборе данных

Следует помнить, что результатом прогноза будет factor

Выведем матрицу ошибок классификации

Выведем значения важности переменных в последней модели

🌟 Видео

R: ридж регрессия и идея оценки лямбдыСкачать

Как написать функцию в R?Скачать

Эконометрика Линейная регрессия и корреляцияСкачать