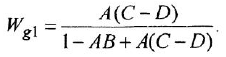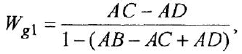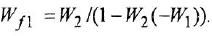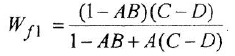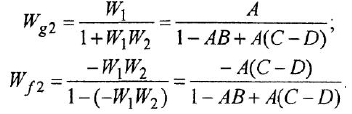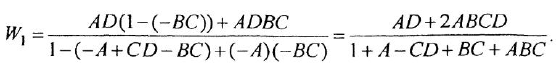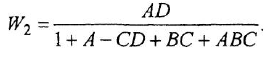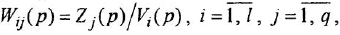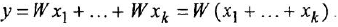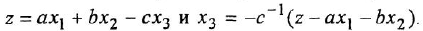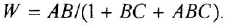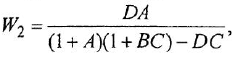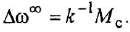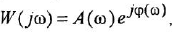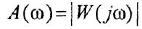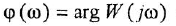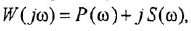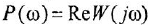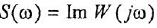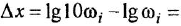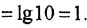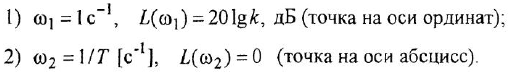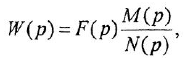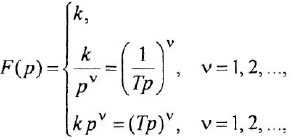1. Вырачитт. член со старшей производной из дифференциального уравнения (1.3) и представить полученное соотношение с помощью сумматора, дифференцирующих и усилительных звеньев.
2. Все низшие производные получить как сигналы на соответствующих выходах последовательно соединенных интегрирующих звеньев.
3 Начальные условия (1.4) представить как постоянные во времени воздействия, приложенные на выходах интегрирующих звеньев.
Пример 1.1. Построить структурную схему системы, описываемой дифференциальным уравнением
с начальными условиями 
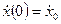
□ Выразим из уравнения член со старшей производной:
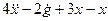
Изобразим схему получения сигнала 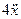
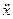
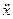
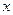
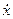
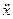
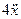
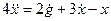
Для этого добавляем к прямой цепи соединение дифференцирующего и усилительного звеньев, которые из входного сигнала g позволяют получить нужный сигнал 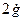
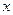
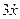
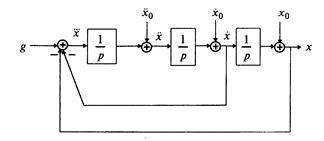
Пример 1.2. Построить структурную схему системы, описываемой дифференциальным уравнением
с начальными условиями 
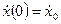
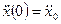
□ Выразим из уравнения член со старшей производной:
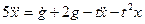
Согласно алгоритму получим структурную схему системы (рис. 1.10).
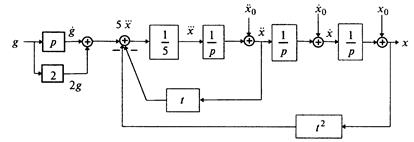
Пример 1.3. Построить структурную схему системы, описываемой дифференциальным уравнением
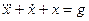
□ Выразим из уравнения член со старшей производной:
и с помощью алгоритма получим схему (рис. 1.11).
2. Составление дифференциального уравнения по структурной схеме. Для записи дифференциального уравнения следует обозначить на схеме все промежуточные сигналы, записать уравнения для каждого звена и для каждого сумматора и из полученной системы дифференциальных и алгебраических уравнений исключить промежуточные переменные кроме входного и выходного сигналов.
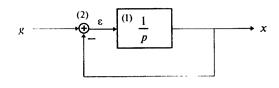
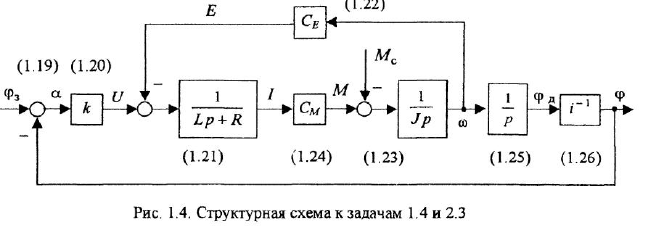
Пример 1.4. Составить дифференциальное уравнение по структурной схеме, изображенной на рис. 1 12.
□ Составим уравнения элементов схемы:
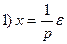
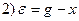
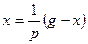
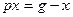
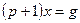
Дифференциальное уравнение системы имеет вид
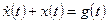
что совпадает с (1.10) при 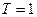
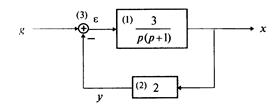
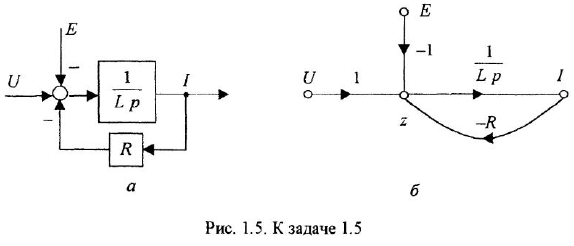
Пример 1.5. Составить дифференциальное уравнение по структурной схеме, представленной на рис. 1.13.
□ Составим уравнения элементов схемы:
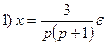
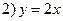
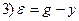
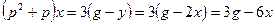
Переходя от операторной формы записи дифференциального уравнения к обычной, получаем
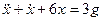
- Примеры решения задач по ТАУ
- ТАУ
- Построение структурных схем и сигнальных графов автоматических систем
- Построение структурных схем и М-графов динамических систем
- Пример №1.1.
- Пример №1.2.
- Пример №1.3.
- Пример №1.4.
- Пример №1.5.
- Анализ структурных схем. Передаточные функции типовых соединений звеньев САУ
- Теорема Мейсона (Мэзона)
- Анализ установившегося режима по структурной схеме при постоянных входных воздействиях
- Пример №2.1.
- Пример №2.2.
- Пример №2.3.
- Преобразование структурных схем. Эквивалентные структурные преобразования
- Операция инверсии
- Пример №3.1.
- Пример №3.2.
- Пример №3.3.
- Пример №3.4.
- Пример №3.5.
- Пример №3.6.
- Пример №3.7.
- Построение и анализ логарифмических частотных характеристик. Логарифмические частотные характеристики
- Получение структурной схемы по уравнениям
- Построение структурной схемы по системе алгебраических уравнений
- Построение структурной схемы по системе дифференциальных уравнений
- 🎥 Видео
Видео:Как в MATLAB Simulink моделировать уравнения (Структурная схема САУ)Скачать

Примеры решения задач по ТАУ
Здравствуйте на этой странице я собрала теорию и практику с примерами решения задач по предмету теория автоматического управления с решением по каждой теме, чтобы вы смогли освежить знания!
| Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу! |
Видео:Как строить структурные формулы быстро, как ФЛЭШ — Мое полное РуководствоСкачать

ТАУ
Теория автоматического управления является основной общепрофессиональной дисциплиной направления подготовки дипломированного специалиста «Автоматизированные технологии и производства».
Основной целью автоматизации является исключение непосредственного участия человека в управлении производственными процессами и другими техническими объектами.
В настоящее время автоматизация технологических процессов представляет собой одно из важнейших средств роста эффективности производства, интенсификации развития народного хозяйства. Таким образом, задача изучения дисциплины «Теория автоматического управления» состоит в освоении основных принципов построения и функционирования автоматических систем управления на базе современных математических методов и технических средств.
Построение структурных схем и сигнальных графов автоматических систем
В теории систем автоматического управления (САУ) широко используют понятие звена, под которым понимают некоторый физический элемент системы (усилитель, двигатель, датчик и т. п.) либо формально выделенную часть математической модели системы (например, уравнение равновесия напряжений якорной цепи двигателя), для которых указаны входные (одна или несколько) и выходная (обычно одна) переменные. При этом говорят, что звено преобразует входные переменные, т. е. приложенные к звену внешние воздействия, в выходную переменную — реакцию. В математическом плане обобщением понятий САУ и звена САУ является понятие динамической системы.
Возможно эта страница вам будет полезна:
Дифференциальное уравнение (ДУ) линейной динамической системы с одним входом и одним выходом записывается в классической форме следующим образом:
Здесь 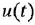
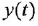
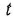
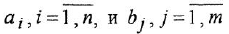
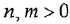
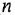
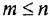
полиномы степеней, соответственно, 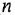
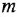
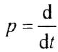
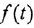
Определим формально операторную передаточную функцию (ОПФ) 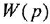
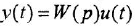
Преобразование ДУ (1.1) по Лапласу при нулевых начальных условиях (ННУ) дает
(использована теорема об изображении производной при ННУ: если
a 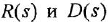
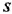
Передаточной функцией (ПФ) 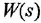
Отсюда в силу уравнения (1.4) и с учетом (1.3) получаем:
т. е. ПФ совпадает с ОПФ с точностью до обозначения аргумента
В связи с этим в дальнейшем будем использовать одно и го же обозначение, например 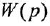
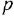
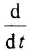
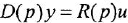
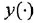
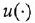
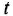
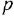
С учетом сказанного рекомендуется следующая методика нахождения ПФ поДУ( 1.1), не требующая применения преобразования Лапласа:
- Заменить в уравнении (1.1)
на
и представить это уравнение в форме (1.2).
- Перейти из временной области в комплексную, просто заменив
и
на
и
.
- Найти ПФ как
.
Если система имеет несколько входов и/или выходов, т. е. является многомерной, то уместно говорить о множестве передаточных функций, связывающих каждый вход 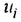
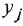
Все они имеют один и тот же знаменатель (если не производить сокращения одинаковых нулей и полюсов) и, в общем случае, разные числители:
Теперь приведем передаточные функции наиболее важных типовых звеньев систем автоматического управления. 1 Пропорциональное звено:
где 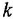
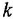
где 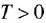
В качестве обобщения можно рассматривать интегрирующее звено произвольного порядка:
- Дифференцирующее звено:
Обобщенное дифференцирующее звено:
где 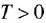
- Апериодическое звено 2-го порядка:
где 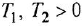
где 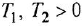
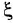
где 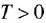
Часто в передаточных функциях звеньев 4, 6, 7 и 8 вместо единицы пишут коэффициент передачи к.
Построение структурных схем и М-графов динамических систем
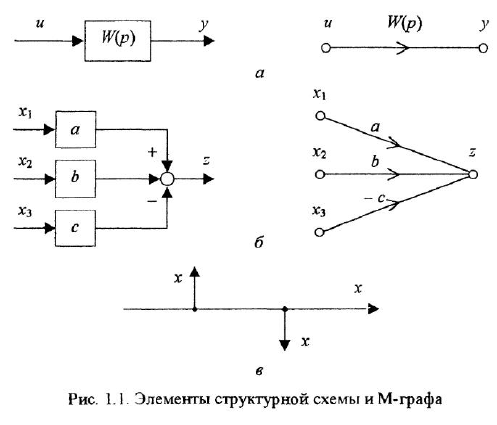
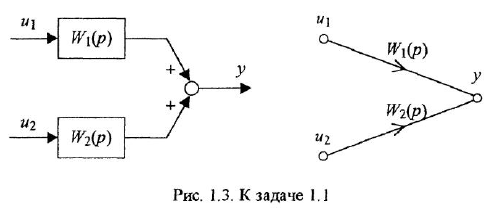
При анализе и синтезе систем автоматического управления часто прибегают к графическом)’ изображению уравнений, описывающих систему. Для этой цели обычно используют структурные схемы и, реже, сигнальные графы В структурной схеме переменные обозначаются отрезками прямых или ломаными линиями, оканчивающимися стрелками В графе каждой переменной соответствует некоторая вершина. Мы будем рассматривать только одну разновидность сигнальных графов, а именно граф Мейсона (Мэзона), или, короче, М-граф
Уравнение звена вила 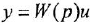
В вершину графа могут входить несколько дуг. В этом случае действует следующее соглашение: переменная, отождествляемая с вершиной, в которую входят дуги, равна взвешенной сумме переменных, соответствующих вершинам, из которых эти дуги исходят, причем в качестве весовых коэффициентов выступают передачи дуг. Так, М-граф, приведенный на рис. 11,6, соответствует уравнению 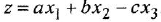
Часто одна и та же переменная входит в несколько уравнений Чтобы в структурной схеме иметь возможность использовать какую-либо переменную в качестве входа сразу нескольких звеньев, применяют специализированный элемент — отвод. Это линия, отходящая от основной в какой-либо точке и обозначающая ту же переменную, что и основная линия (см. рис. 1.1, в, где показаны два отвода). Начало отвода отмечается «жирной» точкой.
Если в структурной схеме имеется горизонтальная цепочка звеньев, чередующихся с сумматорами, то обычно знаки «плюс» или «минус» ставят не у всех стрелок, входящих в сумматоры, а только у тех, которые подходят к данной цепочке извне (см., например, три сумматора между переменными 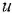
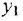
Пусть система задана некоторым числом алгебраических и дифференциальных уравнений. Чтобы построить по ним структурную схему и М-граф системы, рекомендуется выполнить следующие действия:
- В дифференциальных уравнениях заменить
переменной
.
- Полагая, что каждому уравнению соответствует некоторое звено системы, назначить для него выходную и входные переменные При этом часто удобно руководствоваться физическими соображениями и представлениями о причинно-следственных связях между неременными Например, если речь идет об уравнении электрической или электромагнитной цепи, то естественно считать входной величиной напряжение (ЭДС) источника, а выходной — ток. Для уравнения механического вращательного движения входными переменными будут движущий момент и момент сопротивления, а выходной — угловая скорость.
- В каждом уравнении (уравнении
-го звена) выразить выходную переменную
— через входные
(
— число входов):
При этом выражения 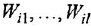
- По каждому уравнению вида (1.15) изобразить М-граф, для чего:
а) нанести на рисунок вершины, соответствующие переменным 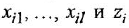
б) из каждой вершины 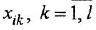
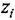
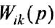
Поскольку правая часть уравнения (1.15) представляет собой алгебраическую сумму, для изображения соответствующей структурной схемы необходим сумматор. В результате получается схема, подобная той, что показана на рис. 11, б Таким образом, если звено имеет один вход, то ему соответствуют структурная схема и М-граф аналогичные тем, что приведены на рис. 1.1, в Нел и же входов несколько, то звену (уравнению) соответствует структурная схема и граф, содержащие несколько звеньев (дуг), причем в структурной схеме обязательно появится сумматор
Уравнения, по которым строится структурная схема или граф, связаны между собой, так как содержат общие переменные Это должно быть ясно отражено и в самой схеме (графе), а именно: в графе не должно быть двух вершин с одинаковыми именами переменных, а в структурной схеме линии, соответствующие одной и той же переменной, должны либо совпадать (так что выход одного звена является входом другого), либо выступать одна по отношению к другой как основная линия и отвод.
Нецелесообразно изображать систему исходных уравнений в виде набора отдельных фрагментов структурной схемы: после этого все равно придется проводить между ними линии связи.
Удобнее рисовать схему (граф) последовательно, используя то обстоятельство, что входными переменными любого звена являются, как правило, выходные переменные других звеньев.
Конечно, входами могут быть и внешние воздействия рассматриваемой системы, т. е независимые переменные, не являющиеся выходами каких-либо звеньев на структурной схеме таким переменным соответствуют стрелки, не исходящие ни из каких звеньев, а в графе — вершины, не имеющие входящих дуг.
В детализированной структурной схеме (ДСС) [3] используются только элементарные звенья — пропорциональные, интегрирующие и дифференцирующие, а также сумматоры. Если для всех передаточных функций системы, связывающих каждый вход с каждым выходом, выполнено условие реализуемости (степень полинома числителя не превышает степени полинома знаменателя), то система может быть описана в виде ДСС, состоящей только из безынерционных (пропорциональных и суммирующих) и интегрирующих звеньев [4]. Для этого рекомендуется пользоваться следующей методикой:
- Представить математическую модель системы
-го порядка в виде совокупности дифференциальных уравнений 1-го порядка (один из способов сделать это состоит в построении гак называемых канонических форм уравнений состояния [3D и, возможно, еще ряда алгебраических уравнений:
Здесь 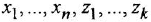
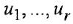
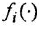
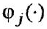
- Заменив
переменной
, переписать (1.16) в виде
Предостережение. Переходя от уравнения (1.17) к уравнению (1.18), не следует приводить подобные члены, содержащие переменную 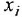
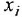
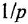
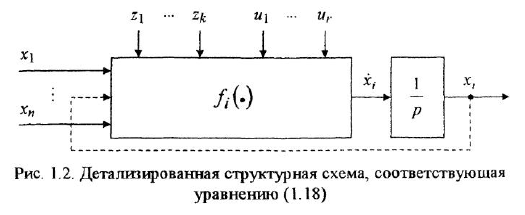
- По уравнениям (1.17), (1.18) изобразить ДСС, принимая во внимание, что уравнению (1.18) соответствует схема, показанная на рис 1.2.
Сформулированная методика сохраняет силу и при построении детализированного М-графа. Имеется, однако, тонкость: чтобы графически изобразить 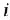
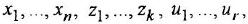
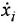
Пример №1.1.
Записать в самом общем виде уравнение, выражающее зависимость выходной величины у линейной динамической системы от входных величин 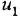
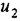
Решение:
Обозначим передаточные функции, связывающие выход с каждым из входов, как 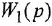
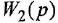
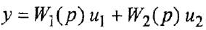
Пример №1.2.
Определить ПФ системы с одним входом 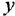
Решение:
Производя замену 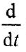
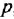
после чего переходим в комплексную область:
откуда получается искомая ПФ
Пример №1.3.
По передаточной функции
системы с одним входом и одним выходом записать ее дифференциальное уравнение.
Решение:
Обозначив выходную и входную переменные системы как 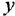
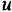
Освобождаясь от дробей и заменяя 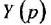
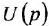
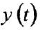
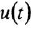
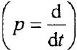
и в классической:
Пример №1.4.
Изобразить структурную схему следящей системы по приведенным ниже уравнениям ее функциональных элементов:
где 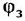
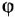
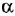
• Регулятор и усилительно-преобразовательное устройство:
где 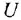
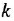
• Двигатель постоянного тока.
где 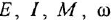
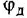
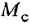
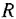
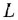
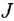
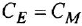
где 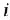
Решение:
Структурная схема, построенная по уравнениям (1.19)-(1 26), показана на рис. 1.4. На ней для большей ясности рядом со звеньями написаны номера соответствующих уравнений. Последовательность изображения уравнений может быть, например, следующей: (1.19)-(1.21), (1.24), (1.23), (1.22), (1.25), (1.26).
Графическое изображение уравнений (1.20), (1.22) и (1 24) затруднений не вызывает — это пропорциональные звенья. Наличие разности в правой части уравнения (1.19) указывает на то, что необходим сумматор с двумя входами Во всех дифференциальных уравнениях заменяем 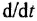
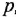
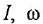
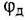
т. е им будут соответствовать интегрирующие звенья с передачей 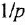
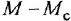
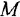
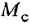
Наибольшую трудность вызывает графическая интерпретация уравнения якорной цепи двигателя (1.21). После замены 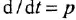
Первый из приведенных вариантов предпочтителен, поскольку в этом случае, во-первых, в структурной схеме будет на одно звено меньше, а во-вторых, последний вариант создает иллюзию того, что порядок системы на единицу выше, чем на самом деле
Замечание. Передаточную функцию
связывающую переменные 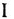
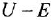
Возможно эта страница вам будет полезна:
Пример №1.5.
По уравнению (1.21) изобразить ДОС и детализированный граф.
Решение:
Перепишем (1.21) в форме уравнения (116): 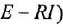
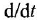
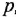
Заметим, что переменная 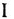
Чтобы изобразить М-граф, нанесем на рисунок вершины для переменных
после чего проведем ребра с соответствующими передачами. Результат показан на рис. 1.5, б.
Полезно сравнить структурную схему и М-граф, соответствующие одному и тому же уравнению. Это, во-первых, поможет читателю в дальнейшем избежать распространенной ошибки — смешивания в одном рисунке элементов структурной схемы и графа, а во-вторых, позволит ему при необходимости легко изобразить по М-графу соответствующую структурную схему, и наоборот.
Анализ структурных схем. Передаточные функции типовых соединений звеньев САУ
Типовыми соединениями звеньев в структурных схемах являются последовательное (рис. 2.1, д), параллельное, или согласно-параллельное (рис. 2.1,6), и соединение с обратной связью, или встречно-параллельное (рис. 2.1, в). Каждое из этих соединений можно рассматривать как одно звено, считая его входной и выходной величинами, соответственно, переменные 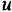
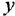
Необходимо твердо усвоить формулы для определения передаточной функции
типового соединения по передаточным функциям звеньев, образующих это соединение:
(Если какая-либо из переменных 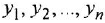
• Соединение с обратной связью:
В последней формуле необходимо выбирать знак «плюс» в случае отрицательной обратной связи и «минус» — в случае положительной. Отметим, что в этой формуле выражение 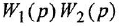
Если структурная схема содержит только типовые соединения, то, как бы сложна ни была эта схема, по ней всегда можно определить передаточную функцию, связывающую заданные переменные, путем последовательного применения формул (2.1)-(2.3). Если же, кроме типовых, есть соединения с более сложной топологией (подробнее об этом см. в 3 1), то необходимо либо использовать теорему Мейсона, рассматриваемую в 2.2, либо применить метод эквивалентных структурных преобразований, излагаемый в 3.1
Теорема Мейсона (Мэзона)
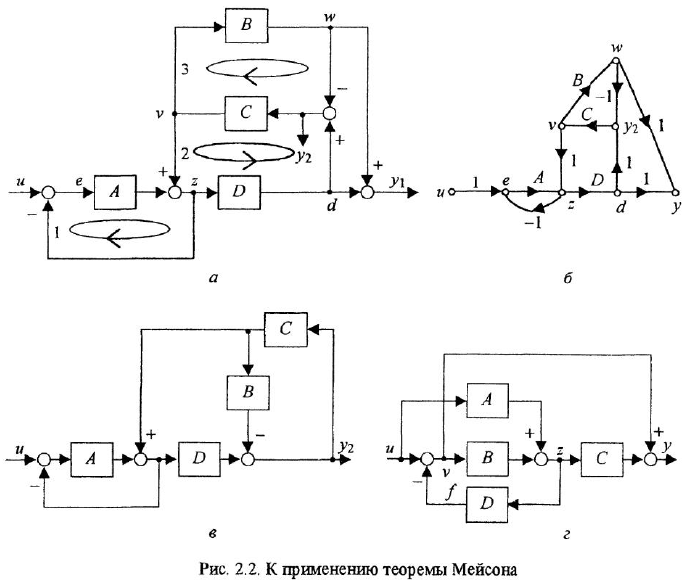
Теорема Мейсона позволяет определить передаточную функцию, связывающую любые две переменные структурной схемы или М-графа. Поскольку первоначально теорема была сформулирована для графов, а затем распространена на структурные схемы, уточним некоторые топологические термины, знание которых необходимо для правильного применения этой теоремы.
Маршрутом в теории графов называют последовательность ребер, в которой соседние ребра инцидентны одной и той же вершине (напомним, что вершина 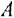
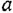
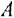
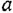
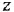
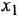
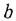
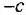
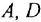
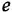
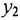
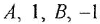
Путь — это маршрут без повторяющихся ребер и вершин На рис. 2.2, б последовательность ребер с передачами 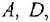
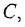
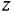
Передачей пути называется произведение передач всех звеньев (в графе — ребер), образующих этот путь, причем необходимо учитывать и знаки, с ко-
торыми переменные данного пути входят в сумматоры, встречающиеся на этом пути. Па рис 2.2, а, б путь между переменными 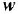
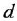
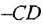
Контуром как в графе, так и в структурной схеме называют замкнутый путь. Для графа это означает, что начальная и конечная вершины пути совпадают.
Передача контура — это произведение передач всех звеньев (или ребер), образующих контур, с учетом знаков в сумматорах Например, контур в графе на рис. 1.5, б имеет передачу 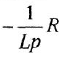
Говорят, что контур не касается другого контура или пути, если он не имеет с ним общих переменных. На рис 2.2, а, б контур с передачей 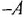
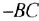
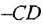
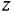
Согласно теореме Мейсона, передача, связывающая некоторую «входную» переменную 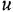
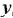
Обозначения, использованные в формулах (2.4)-(2.6), имеют следующий смысл: 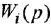
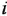
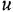
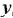
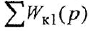
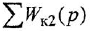
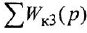
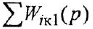
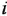
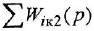
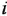
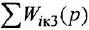
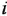
Заметим, что два пути или два контура могут частично совпадать; тем не менее, если они различаются хотя бы одним звеном (ребром), то это рахпич-ные пути или контуры.
Решение любой задачи, требующей применения теоремы Мейсона, следует начинать с анализа структурной схемы или М-графа. Если схема сложна, то рекомендуется сначала выписать передачи всех путей, связывающих заданные переменные, и передачи всех контуров, отметив специально «некасающиеся» контуры После этого можно непосредственно записывать искомую передаточную функцию в соответствии с формулами (2 4)-(2.6).
Хотя при определении передаточных функций по теореме Мейсона в качестве входной переменной практически всегда выступает какое-либо внешнее воздействие, ничто не мешает применять эту теорему в ситуации, когда входом является некоторая «внутренняя» переменная структурной схемы. В этом случае надо лишь «усечь» схему, исключив из нее все пути, направленные к указанной входной переменной от заданного выхода и от внешних входных воздействий.
Удобство теоремы Мейсона заключается в возможности быстро записать требуемую передаточную функцию без многократного перерисовывания структурной схемы, что часто бывает необходимо в случае применения альтернативного метода структурных преобразований (см. 3.1) Вместе с тем, с ростом сложности схемы резко возрастает опасность «пропустить» при ее анализе какой-нибудь путь или контур либо не заметить факта «некасания» Поэтому в целом метод структурных преобразований считается более надежным способом определения передаточной функции по структурной схеме
Анализ установившегося режима по структурной схеме при постоянных входных воздействиях
Для исследования динамических систем, в том числе на ЭВМ, бывает важно уметь анализировать установившийся режим при постоянных внешних воздействиях Это можно делать различными способами — например, с помощью алгебраических методов пространства состояний. Здесь мы рассмотрим простой способ, позволяющий определить установившиеся значения всех переменных системы по структурной схеме.
Пусть система асимптотически устойчива (изложение методов анализа устойчивости выходит за рамки данного учебного пособия) Тогда, если все входные (внешние) воздействия постоянны, то с течением времени (теоретически — при 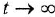
- Если схема содержит интегрирующее звено, описываемое, как известно, уравнением
, то из
(индекс
служит обозначением установившегося режима) следует, что
. Таким образом, в асимптотически устойчивой системе с постоянными внешними воздействиями входные переменные всех интегрирующих звеньев в установитиемся режиме равны нулю.
2 Если в схеме имеется дифференцирующее звено, описываемое уравнением 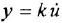
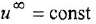
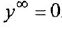
Большинство звеньев структурной схемы — это позиционные звенья, описываемые передаточными функциями (1.5), (I 10), (1 12) и (I 13), причем в трех последних в общем случае присутствует коэффициент передачи 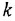
Коэффициент передачи к звена (системы) может быть определен двояко:
а) 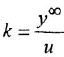
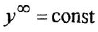
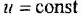
б) 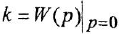
Последнее выражение — это одновременно и практический способ определения коэффициента передачи.
Общим свойством позиционных звеньев является то, что при подаче на вход такого звена постоянной величины на его выходе с течением времени также устанавливается постоянное значение. ПФ позиционного звена в установившемся режиме вырождается в коэффициент передачи 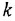
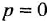
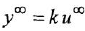
Консервативное звено с ПФ (1.14) также относится к позиционным, но, в отличие от остальных, не является асимптотически устойчивым. При наличии в схеме консервативного звена (или эквивалентного ему встречно-параллельного соединения интегрирующего звена 2-го порядка и пропорционального звена) в системе в установившемся режиме будут наблюдаться незатухающие колебания, т. е. по крайней мере некоторые переменные будут изменяться по гармоническому закону. Анализ такого установившегося режима выходит за рамки излагаемого здесь метода.
В заключение отметим, что отводы по переменным, установившиеся значения которых равны нулю, при анализе установившегося режима можно не учитывать.
Возможно эта страница вам будет полезна:
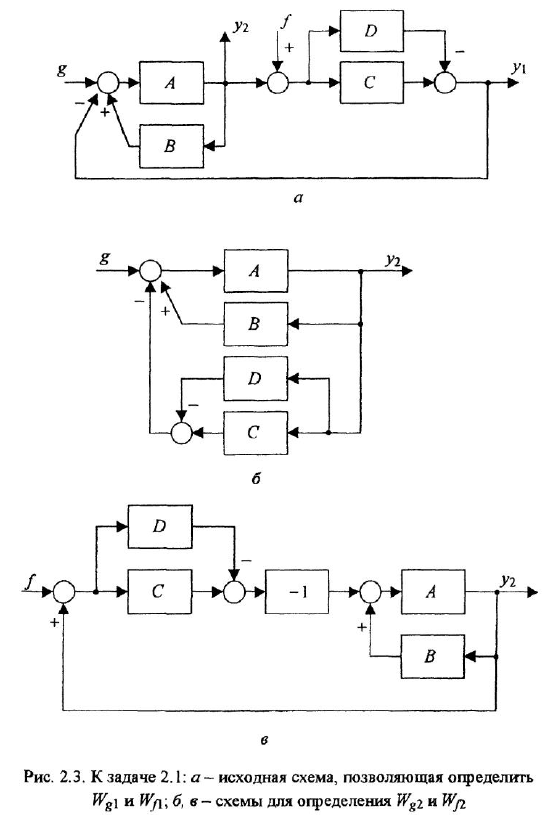
Пример №2.1.
По структурной схеме (рис 2.3, а) определить передаточные функции 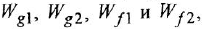
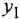
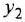
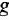
Решение:
Сначала найдем ПФ 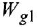
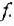
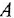
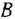
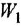
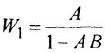
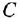
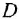
согласно-параллельное соединение; в соответствии с формулой (2.2) его 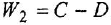
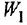
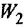
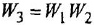
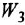
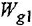
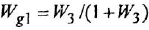
Для сравнения получим искомую ПФ иначе — с помощью теоремы Мейсона. От 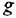
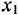
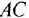
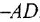
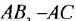
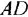
что, разумеется, совпадает с ранее полученным выражением.
Чтобы найти ПФ 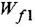
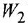
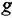
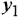
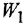
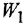
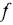
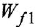
До сих пор на структурных схемах выходная величина всегда изображалась стрелкой, заканчивающей горизонтальную цепочку звеньев, берущую начало от места приложения задающего воздействия. Если же в качестве выхода рассматривается какая-либо «внутренняя» переменная (в данной задаче — 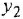
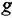
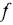
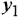
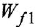
на рис. 2.3, в прямая связь имеет передачу — 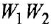
С учетом сказанного, легко записать искомые ПФ
Обращаем внимание читателя на то, что все четыре найденные передаточные функции имеют, как это всегда и должно быть, одинаковые знаменатели.
Чтобы найти ПФ 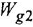
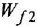
Пример №2.2.
С помощью теоремы Мейсона по структурной схеме или М-графу, изображенным на рис. 2.2, а и б, определить передаточные функции 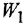
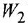
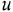
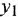
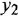
Решение:
Определим ПФ 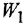
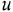
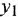
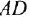
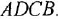
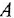
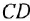
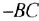
При нахождении 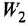
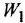
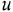
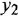
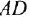
Пример №2.3.
С помощью теоремы Мейсона определить передачу между переменными 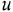
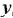
Решение:
В схеме только один контур, но четыре пути: с передачами, соответственно, 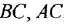
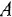
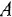
Возможно эта страница вам будет полезна:
Преобразование структурных схем. Эквивалентные структурные преобразования
Если в структурной схеме имеются не только типовые соединения звеньев (см. 2.1), но и другие, более сложные, то при необходимости определить передаточную функцию, связывающую заданные переменные, можно поступить различным образом: воспользоваться теоремой Мейсона (о ее достоинствах и недостатках было сказано ранее) либо применить метод эквивалентных преобразований структурных схем (короче — метод структурных преобразований), излагаемый далее. Этот метод, как показывает практика преподавания, не так легок для начального освоения, как теорема Мейсона, и даже может показаться громоздким, но в действительности после приобретения необходимых навыков становится удобным, эффективным и надежным инструментом анализа систем. Знание этого метода обязательно для специалиста в области автоматического управления. Рассмотрим сущность метода эквивалентных структурных преобразований.
Обычно в схеме можно выделить две части, не обязательно компактные одна состоит только из типовых соединений, к которым, следовательно, сразу могут быть применены формулы (2 1)—(2.3) для определения передаточных функций, другая же — назовем ее преобразуемой частью — содержит различного рода нетиповые соединения звеньев. В чем особенность таких соединений, и почему они являются предметом специального рассмотрения0
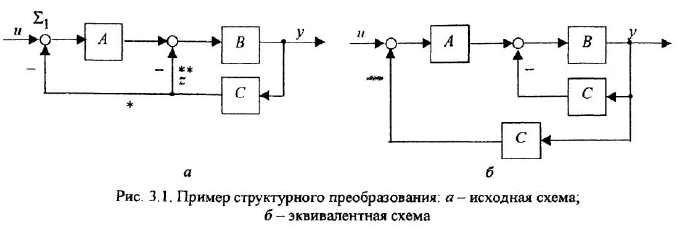
На рис 3.1, а показана структурная схема, в которой вообще нет типовых соединений. Если бы в этой схеме отсутствоват отвод «*» (конечно, вместе с сумматором 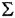
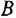
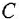
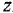
Возникает вопрос: нельзя ли заменить эту схему другой так, чтобы ее передаточная функция не изменилась, но отвод «*» шел не с выхода звена с передачей 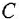
соединения, а передаточная функция, связывающая переменные 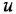
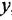
Приведение схемы к типовому виду осуществляется выполнением некоторого количества операций преобразования. После выполнения любой из этих операций новая схема должна в определенном смысле быть эквивалентна предыдущей Пусть та часть (фрагмент) структурной схемы, над которой совершается операция преобразования, имеет 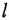
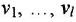
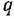

связывающих каждый вход 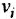
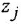
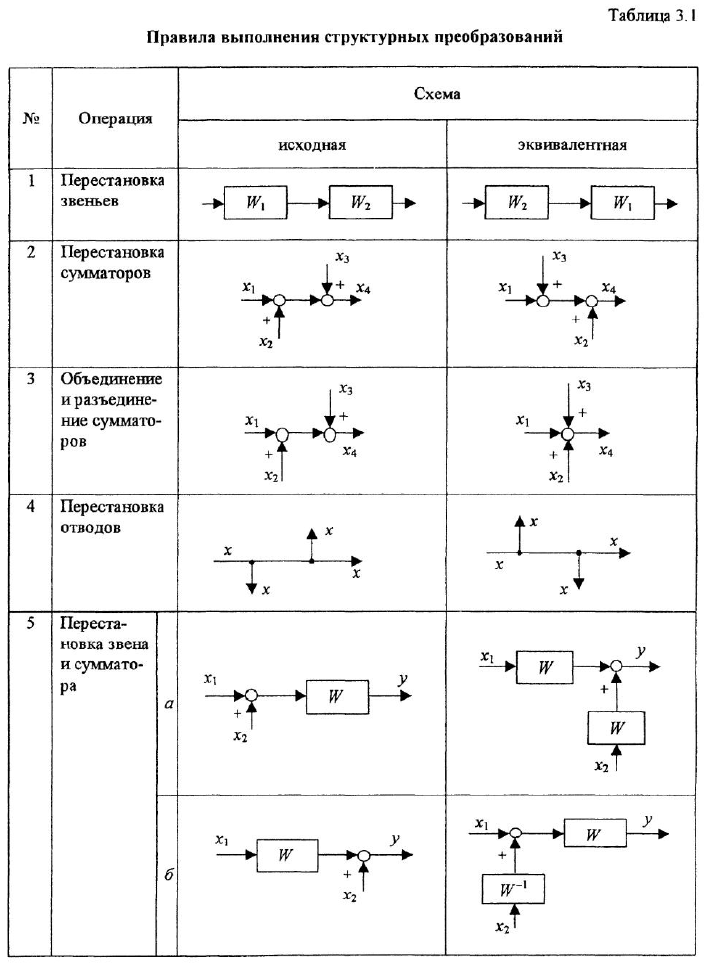
В табл. 3.1 приведены правила, по которым выполняются структурные преобразования. Подавляющее большинство приведенных здесь операций -это различного рода перестановки: звеньев, сумматоров и отводов. Для пояснения каждой операции в соответствующей горизонтальной графе показаны две схемы: исходная и эквивалентная ей преобразованная Однако как раз в силу эквивалентности всех преобразований каждую пару схем можно просматривать и в обратном порядке, считая эквивалентную схему исходной Например, операция 3 носит двойственный характер: сумматоры можно объединять и, наоборот, разделять.
При начальном изучении табл. 3.1 полезно убедиться в корректности каждой операции. Для этого рекомендуется проверить совпадение передаточных функций, связывающих каждый вход с каждым выходом в исходной
и эквивалентной схемах. Чтобы получить требуемую ПФ, необходимо просто «пройти» вдоль пути, связывающего данный вход с данным выходом, перемножая передачи всех звеньев этого пути и учитывая знаки в сумматорах. Можно поступить и иначе, в обеих схемах для каждой выходной переменной записать уравнение, описывающее зависимость этой переменной от всех входных переменных, после чего сравнить эти уравнения.
Особо подчеркнем следующее обстоятельство: приведенные в табл 3.1 правила выполнения операций не предназначены для запоминания. Необходимо просто понять логику построения эквивалентной схемы по имеющейся исходной и всякий раз при решении конкретной задачи поступать аналогично.
Рассмотрим теперь правила выполнения отдельных операций Все множество приведенных в табл. 3.1 операций можно условно разделить на три группы Первую из них составляют простейшие операции 1-4, которые вряд ли нуждаются в пояснениях.
Группу основных операций составляют операции 5-7. Именно они являются главным инструментом преобразования структурных схем. Рассмотрим перестановку звена и сумматора — например, в случае, когда сумматор стоит перед звеном (в табл. 3.1 — операция 5, вариант а). Если просто поменять местами сумматор и звено с передачей 
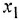

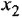

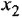

Аналогично рассуждаем при обосновании правила перестановки звена и отвода. Рассмотрим операцию 6, вариант а. Просто поменять местами звено и отвод нельзя: в этом случае отвод будет по переменной 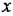
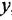
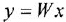

Перестановка сумматора и отвода — наиболее сложная из операций преобразования структурных схем, и ее по возможности следует избегать. Здесь тоже есть два варианта взаимного расположения переставляемых элементов (варианты а и б операции 7 в табл. 3.1) В связи с этим следует со всей определенностью сказать, что объективная необходимость в выполнении перестановки по варианту б встречается крайне редко Бели при анализе конкретной схемы выясняется, что без перестановки сумматора и отвода обойтись нельзя, то необходимо, прежде всего, искать возможность выполнить перестановку по варианту а, такая возможность, скорее всего, существует.
Обращаем внимание на то, что, согласно правилу выполнения данной операции, в эквивалентной схеме вместо отвода по переменной 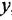
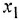
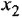
Однако, оказывается, перестановку сумматора и отвода можно выполнить гораздо более простым способом, исключающим появление дополнительного сумматора, а значит, и не требующим последующих операций по упрощению схемы. Суть этого способа (отразить его в табл. 3.1 не представляется возможным) состоит в следующем. В исходной системе отвод по переменной у, или в данном случае удобнее сказать — сама переменная 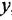

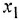
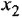

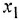
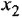

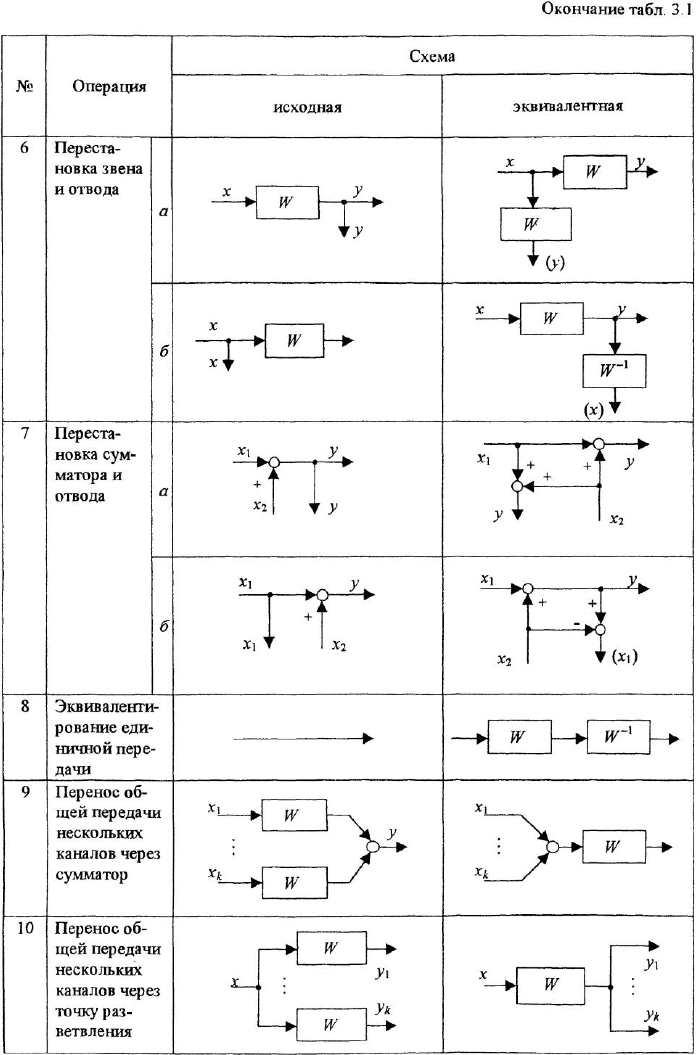
Последнюю группу в табл. 3.1 составляют операции 8-10, которые можно назвать вспомогательными. Справедливость операций 8^и 10 очевидна, при этом заметим, что величины 
В чем польза трех последних операций? Рассмотрим более внимательно операцию 9. Ее смысл заключается в возможности выноса общей передачи из нескольких суммирующихся каналов (имеются в виду линии, входящие в сумматор) в канон за сумматором. Очевидно, что это упрощает схему, особенно если число входящих в сумматор каналов велико. Однако, возможно, еще большая польза этой операции состоит в другом. Если, наоборот, эквивалентную схему принять за исходную, то операция 9 трактуется по-другому: передачу звена, расположенного за сумматором, можно поместить в каждый из суммирующихся каналов Это позволяет иначе взглятть на уже рассмотренную операцию 5 перестановки звена и сумматора (в варианте а). Очевидно, что она полностью совпадает с операцией 9, и, следовательно, если в схеме последовательно расположены сумматор и звено, то операцию 5 над ними можно трактовать уже не как взаимную перестановку, а как «ввод» звена в каждый из каналов — это правило легко запоминается учащимися
Аналогично обстоит дело с операцией 10. Если рассматривать приведенную в табл 3.1 пару схем слева направо, то правило звучит так: общую передачу всех связей, отходящих от точки разветвления, можно внести в связь перед этой точкой. Рассматривая эти же схемы в обратном порядке, можно прийти к следующему выводу: передачу звена, стоящего до точки разветвления, можно внести во все отходящие от этой точки связи. Знание этого правила позволяет, не задумываясь, выполнять операцию 6 перестановки звена и отвода (вариант а).
Операция 8 удобна тем, что позволяет искусственно создать в какой-либо связи звено с требуемой передачей — чтобы получить возможность вынести эту передачу из двух или более связей, т. е. выполнить операцию 9 или 10.
В заключение укажем на еще одно правило, которое бывает полезно при упрощении схем и выполнении других процедур их преобразования к заданному виду: уравнения, описывающие систему, не изменятся, если в структурной схеме у всех переменных, связанных с каким-либо сумматором, изменить знак на противоположный. Другими словами, можно изменить знаки у всех стрелок, входящих в сумматор, и поставить звено с передачей -1 в связь, выходящую из сумматора. Эта операция, по существу, является частным случаем операции 9 при 
Знание правил структурных преобразований не дает, однако, ответа на вопрос, в каком порядке следует преобразовывать схему к типовому виду при решении конкретной задачи. Ответить определенно на него невозможно, поскольку задачи такого типа решаются, как правило, не единственным образом То, какие именно операции и в какой последовательности будут использованы, зависит как от многообразия вариантов решения, так и от опыта и, не в последнюю очередь, от личных предпочтений специалиста, выполняющего структурные преобразования. Нет нужды доказывать, что при наличии нескольких возможных алгоритмов решения задачи необходимо выбирать наиболее простой.
Несмотря на сказанное, некоторые общие рекомендации относительно алгоритма преобразования структурных схем все же можно дать. Прежде всего, необходимо каждое имеющееся в схеме типовое соединение звеньев заменить эквивалентным звеном, снабдив его обозначением соответствующей передаточной функции. Затем целесообразно выполнить операции перестановки звена и отвода или/и звена и сумматора (как уже указывалось, операцию перестановки сумматора и отвода без необходимости применять не следует), чтобы в результате образовались новые типовые соединения. Их нужно опять заменить эквивалентными звеньями и т. д. Рекомендуется после каждого этапа преобразований перерисовывать схему с новыми обозначениями.
Возможно эта страница вам будет полезна:
Операция инверсии
Полезным видом структурно-топологических преобразований является операция инверсии. Ее применяют
- а) для приведения структурной схемы к виду, удобному для цифрового и аналогового моделирования, путем устранения дифференцирующих звеньев,
- б) при анализе установившихся режимов для устранения некорректности типа деления на ноль (в передаточных функциях вида /р при р-> 0),
- в) для получения из схемы общего вида некоторых частных структурных схем путем предельного перехода при стремлении какого-либо параметра к бесконечности или к нулю.
Различают инверсию пути и контура. Главной чертой этих операций является изменение направления пути (контура) на противоположное
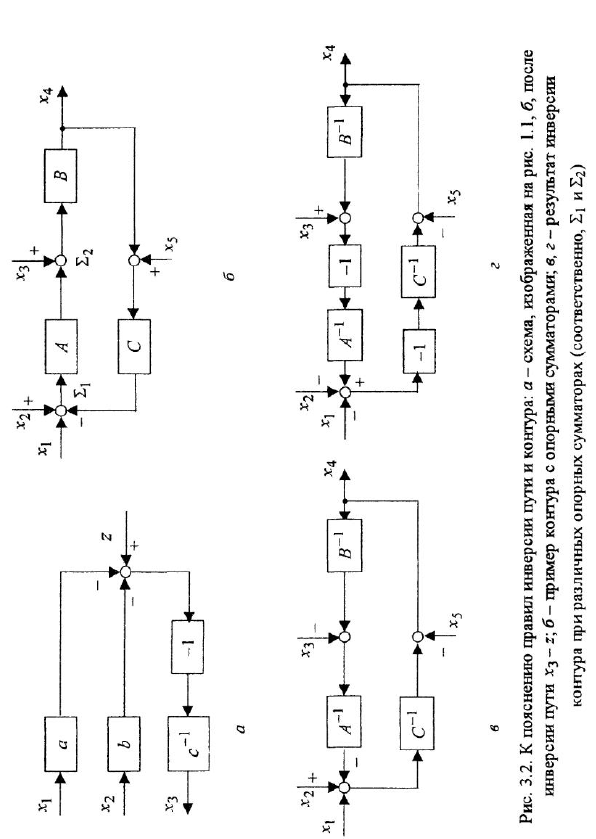
Рассмотрим операцию инверсии пути. Чтобы излагаемое далее правило было более понятно, проиллюстрируем его примером. Пусть требуется про-инвертировать путь между переменными 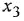
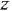
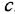
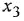
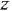
Для рассматриваемого примера результат инверсии показан па рис 3.2, а. Сравнение этой схемы с исходной позволяет лучше усвоить излагаемое далее правило инверсии пути.
Чтобы проинвертировать некоторый путь между двумя переменными структурной схемы, необходимо изменить:
1) направление пути на противоположное;
2) передачи всех звеньев этого пути — на обратные;
3) знаки всех воздействий, подходящих к данному пути, — на противоположные.
Это правило можно рассматривать как алгоритм выполнения данной операции. На первом этапе следует перерисовать схему, изменив направления всех стрелок рассматриваемого пути (и только его!) и пока воздержавшись от записи передач внутри графических изображений звеньев. Далее необходимо записать эти передачи как обратные исходным, причем, если на инвертируемом пути встречаются сумматор и принадлежащая этому же пути стрелка, входящая в сумматор со знаком «минус», то последний следует интерпретировать как звено с передачей -1. В заключение меняют на противоположные знаки, с которыми к рассматриваемому пути подходят (в сумматорах) внешние воздействия, в том числе воздействия от остальной части схемы.
Заметим, что с математической точки зрения инверсия пути соответствует разрешению алгебраического уравнения, описывающего данный путь, относительно новой переменной.
Так, в рассмотренном примере исходной и преобразованной схемам соответствуют следующие два варианта одного и того же уравнения:
Инверсия контура в практическом плане является наиболее важной из двух рассматриваемых здесь операций. Именно она является инструментом решения задач, перечисленных в начале раздела.
Чтобы проинвертировать некоторый контур структурной схемы, необходимо:
1) любой сумматор этого контура принять за опорный (обозначим его 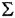
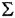
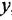
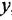
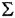
2) направление контура изменить на противоположное; в результате этого прямая связь становится обратной, а обратная — прямой;
3) передачи всех звеньев контура изменить на обратные (как-уже пояснялось, знаки «минус» при входящих в сумматоры стрелках данного контура тоже необходимо рассматривать как звенья этого контура, имеющие передачу -1);
4) знаки прямой и обратной связей изменить на противоположные, вставив звено с передачей -1 непосредственно у опорного сумматора;
5) знаки всех воздействий, подходящих к данному контуру извне, за исключением воздействий, приложенных к опорному сумматору, заменить на противоположные.
Применение этого правила проиллюстрируем на примере контура, изображенного на рис. 3.2, б Рассмотрим два варианта назначения опорного сумматора (приводящие, таким образом, к двум вариантам решения) — они обозначены на схеме как 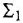
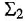
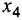
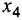
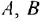

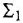
Пусть опорным является сумматор 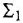
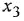
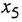
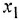
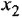
Теперь рассмотрим вариант с опорным сумматором 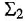
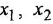
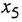
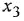
Хотя выбор различных опорных сумматоров привел к различным структурным схемам, эти схемы легко получаются одна из другой изменением знаков всех переменных в сумматорах 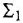
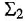
Если требуется привести структурную схему к виду, удобному для моделирования, путем устранения имеющихся в ней дифференцирующих звеньев, то эту задачу можно решить с помощью операции инверсии контура в том случае, если инвертируемый контур не содержит интегрирующих звеньев. В противном случае при замене передач звеньев кон тура на обратные интегрирующие звенья превратятся в дифференцирующие. В такой ситуации делу могут помочь структурные преобразования, а в сложных случаях — применение методов пространства состояний (канонических форм, которые всегда приводят к структурным схемам без дифференциаторов [3]).
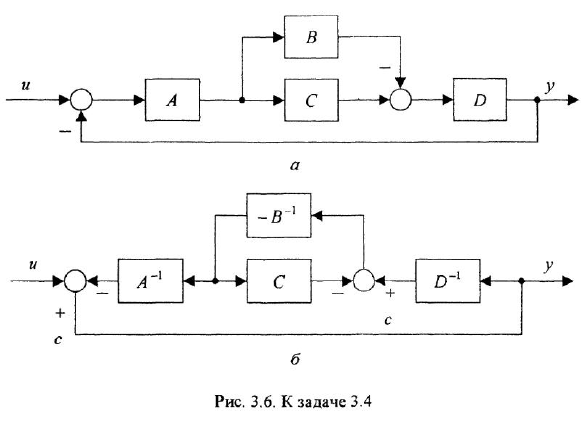
Пример №3.1.
По структурной схеме, изображенной на рис 3.1, а, определить передаточную функцию, связывающую переменные 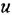
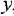

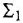
Решение:
На рис. 3.1,6 показан результат решения задачи первым способом. Чтобы получить его, необходимо сначала перерисовать без каких-либо изменений ту часть схемы, которая не подвергается операции преобразования. В данном случае это вся схема за исключением отвода «». Специально обращаем внимание на то, что звено с передачей 


Для решения вторым способом удобно воспользоваться операцией 9 (см. табл. 3.1): убрав звено с передачей 


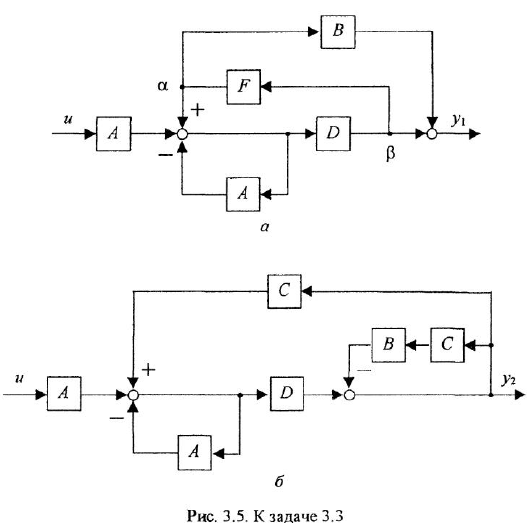
Пример №3.2.
По схеме, изображенной на рис. 2.2, г, определить передаточную функцию от и к у методом структурных преобразований
Решение:
Данная схема является примером случая, когда нельзя обойтись без операции перестановки сумматора и отвода Наиболее быстро задача решается взаимной перестановкой первого (слева) сумматора и отвода по переменной 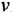
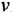
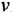
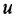
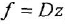
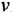
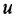
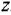
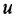
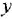
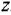
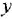
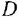
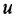
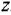
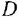

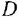

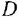
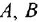
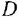
между переменными 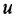
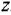
Это выражение после упрощения совпадает с найденным в задаче 2.3
Пример №3.3.
По структурным схемам, приведенным на рис. 2.2, а и в, определить методом структурных преобразований передаточные функции 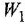
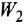
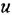
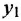
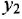
Решение:
Главную трудность при нахождении ПФ 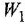
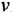
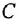
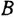
Одновременно сделаем перестановку крайнего левого сумматора и звена с передачей 
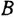


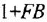
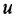
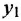
что после подстановки выражения для 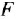
Преобразования схемы на рис. 2.2, в, необходимые для нахождения ПФ 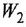


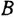
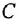
что совпадает с ПФ в задаче 2.2.
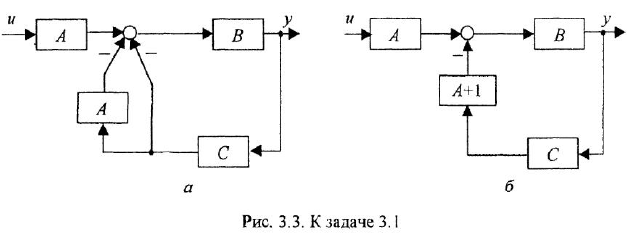
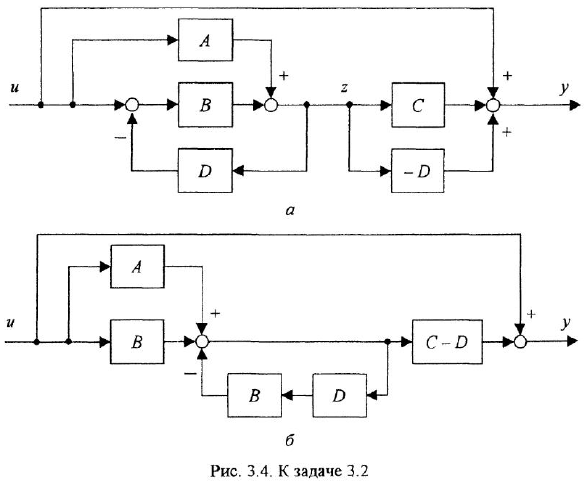
Пример №3.4.
Выполнить инверсию контура 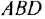
Решение:
Примем левый сумматор за опорный, а переменную 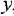
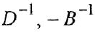
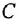
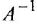
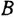

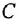
Полезно убедиться, что передаточная функция системы после инверсии не изменилась.
Пример №3.5.
В структурной схеме, изображенной на рис. 2.1, в, с помощью эквивалентных структурных преобразований сделать обратную связь единичной.
Решение:
Задача предназначена для самостоятельного решения Рекомендуется использовать операции 8 и 10 из табл. 3.1.
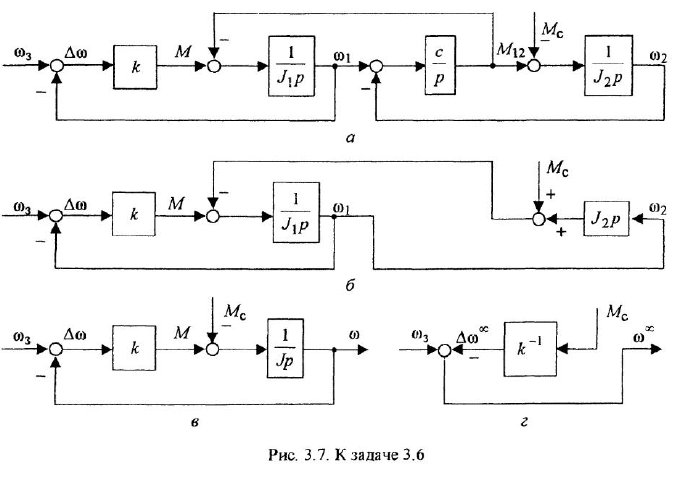
Пример №3.6.
На рис. 3.7, а показана упрошенная структурная схема системы автоматического регулирования скорости электродвигателя постоянного тока, соединенного с рабочим механизмом упругой механической связью, имеющей жесткость с. Требуется с помощью операции инверсии контура: а) получить частную схему для случая жесткой связи двигателя с механизмом 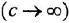
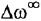
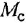
Пояснение Кроме названных, в схеме имеются следующие переменные: 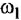
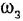
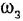
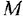
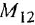
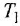
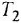
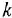
Решение:
Проинвертируем контур, содержащий звенья с передачами 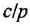
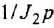
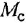
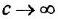
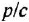
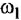
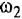
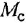
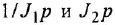
тельной обратной связью, передача которого есть 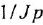
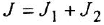
Чтобы решить вторую часть задачи, выполним инверсию полученного контура (ввиду простоты эту операцию не поясняем). Для перехода к схеме установившегося режима достаточно заменить обозначения переменных на установившиеся значения и принять 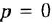
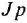
Пример №3.7.
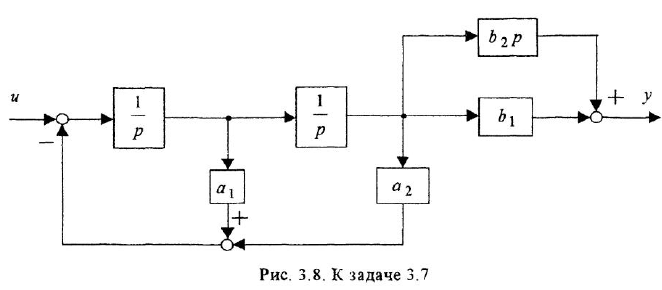
Структурную схему, изображенную на рис. 3.8, привести к виду, удобному для моделирования, устранив дифференцирующее звено.
Решение:
Задача решается путем переноса отвода, идущего на вход звена с передачей 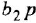
Построение и анализ логарифмических частотных характеристик. Логарифмические частотные характеристики
Математический аппарат частотных характеристик, в особенности — логарифмических частотных характеристик, является весьма эффективным инструментом анализа и синтеза автоматических систем, даже несмотря на наличие мощных методов так называемой «современной теории управления» (методов пространства состояний, вход-выходного подхода и др.) и огромные возможности вычислительной техники. Частотные характеристики благодаря сочетанию строгости, простоты, наглядности и информативности не только являются удобным средством в руках инженера и исследователя, но и, после приобретения достаточного опыта, вырабатывают у специалиста интуицию, необходимую для приближенной оценки динамических свойств систем и поиска методов их улучшения.
Как известно, частотная передаточная функция (ЧПФ) 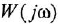
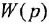
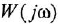
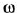
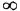
называются, соответственно, амплитудной (АЧХ) и фазовой (ФЧХ) частотными характеристиками. Если же ЧПФ представлена в алгебраической форме
называются, соответственно, вещественной (ВЧХ) и мнимой (МЧХ) частотными характеристиками.
Чтобы построить АФХ, необходимо
1) записать аналитические выражения для 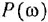
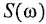
2) задавая некоторые характерные значения 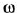
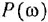
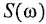
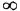
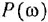
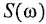
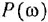
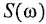
3) задав на комплексной плоскости систему координатных осей 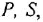
называется логарифмической амплитудной частотной характеристикой (ЛAX) и графически изображается как функция частоты 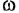
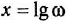
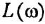
Любой интервал частот 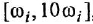
На рис. 4.1 изображена система координат, которой пользуются при построении ЛЧХ. На ней показан пример оцифровки осей, причем для оси абсцисс даны два варианта оцифровки, используемые в литературе: снизу от оси — для 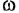

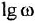
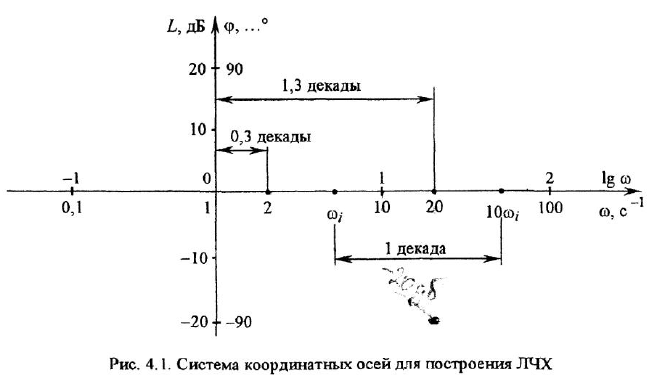
Необходимо уметь правильно отмечать на оси абсцисс точки, соответствующие конкретным значениям частоты. Пусть, например, требуется нанести на ось частот две точки: 2 


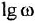




Также необходимо уметь строить в принятом масштабе наклонные участки асимптотических ЛАХ, т е. отрезки прямых, имеющих стандартные коэффициенты наклона Например, чтобы через данную точку провести прямую, имеющую коэффициент наклона -20 дБ/дек, следует найти вторую точку, отстоящую от заданной на 1 декаду вправо и на 20 дБ вниз (либо, наоборот, на 1 декаду влево и на 20 дБ вверх), после чего соединить обе точки отрезком прямой. Коэффициенты наклона 0, ±20 дБ/дек, ±40 дБ/дек… сокращенно обозначают 0, ±1, ±2 . ..
При изучении теории автоматического управления обязательным является знание логарифмических частотных характеристик типовых звеньев САУ, перечисленных в 1.1. Этот материал можно найти в любом учебнике по теории автоматического управления Здесь мы, не приводя графиков ЛЧХ типовых звеньев, отметим их существенные особенности, знание которых облегчает усвоение этого материала.
Общей чертой трех типов звеньев — пропориионального с ПФ (1 5), интегрирующего и дифференцирующего (произвольного порядка), описываемых передаточными функциями (1.7) и (1.9), — является то, что для них как ЛАХ, так и ЛФХ представляют собой прямые При этом ЛАХ пропорционального звена — горизонтальная прямая с ординатой 20 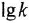
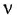
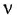
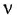
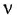
Каждая из этих точек соответствует своей, одной из двух форм записи передаточных функций (1.7) и (1.9) — с использованием коэффициента 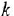
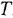
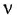
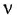
С остальными из перечисленных в 1.1 типовых звеньев дело обстоит сложнее. Для каждого из них различают два вида ЛАХ — точную, описываемую выражением (4.1), и асимптотическую. При компьютерном моделировании САУ с помощью специализированных математических пакетов, например Control System Toolbox системы Matlab, мы имеем возможность рассчитывать и видеть на экране график именно точной ЛАХ исследуемой системы. Однако в практике предварительного инженерного анализа систем и оценки вариантов закона управления обычно имеют дело с асимптотическими ЛАХ, широкое применение которых объясняется простотой их построения даже для весьма сложных систем и богатством заключенной в них информации.
Асимптотическая логарифмическая амплитудная частотная характеристика — это ломаная, отрезки которой являются асимптотами для точной ЛАХ. Для звеньев, описываемых передаточными функциями (1.10), (1.11), (1 13) и (1 14) (апериодическое звено 2-го порядка мы исключаем из рассмотрения, поскольку оно заменяется последовательным соединением двух апериодических звеньев 1-го порядка), асимптотическая ЛАХ состоит из двух асимптот: низкочастотной (к ней точная ЛАХ приближается при 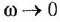
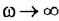
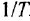
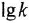
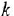
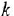
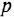
Фазовые характеристики трех звеньев графически представляют собой плавные кривые; они являются следующими функциями частоты: 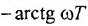
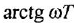
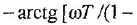
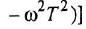
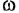
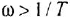
Заметам, что передаточные функции (1 10) и (1.11) апериодического и форсирующего звеньев являются взаимно обратными. Как следствие, их ЛЧХ симметричны друг другу относительно оси частот. То же самое можно сказать об ЛЧХ дифференцирующего и интегрирующего звеньев. В связи с этим набор «типовых» передаточных функций можно расширить, введя в него функции, обратные передаточным функциям (1 13) и (1 14) колебательного и консервативного звеньев. Соответственно, ЛЧХ таких звеньев будут зеркальным отображением ЛЧХ указанных звеньев. Такой расширенный набор позволяет почти любую передаточную функцию, не являющуюся типовой, представить в виде произведения типовых передаточных функций
В процессе анализа САУ часто возникает необходимость в построении ЛЧХ систем с довольно сложной структурой Будем предполагать, что структурная схема системы уже преобразована так, что содержит только типовые соединения Следовательно, возникает задача построения ЛЧХ типовых соединений звеньев по известным ЛЧХ самих этих звеньев
Рассмотрим последовательное соединение Основной результат состоит в том, что как ЛАХ, так и ЛФХ последовательного соединения звеньев могут быть получены суммированием соответствующих характеристик звеньев, образующих это соединение (уточним, что нас интересует, главным образом, графическое сложение частотных характеристик). Это позволяет сравнительно легко строить ЛЧХ длинных цепочек звеньев
На данный результат можно посмотреть и с другой стороны. Среди звеньев структурной схемы могут оказаться и такие, передаточные функции которых не совпадают ни с одной из рассмотренных ранее передаточных функций типовых звеньев. Однако в большинстве случаев такая «сложная» передаточная функция всегда может быть представлена в виде произведения типовых передаточных функций, а значит, ее можно рассматривать как ПФ последовательного соединения типовых звеньев, что позволяет строить ЛЧХ по такой ПФ суммированием «типовых» составляющих.
Несмотря на ясность изложенного подхода, необходимо сделать существенную оговорку. Основные преимущества метода ЛЧХ связаны, в первую очередь, с простотой ручного построения асимптотических ЛАХ типовых звеньев САУ и, как следствие, систем в целом (мы говорим именно о ручном построении как основе предварительных, прикидочных расчетов автоматических систем; впрочем, очень часто расчеты, выполненные с помощью ЛЧХ, являются весьма точными). В отличие от асимптотических ЛАХ, которые можно строить вполне точно с соблюдением необходимых масштабов, фазовые характеристики большинства даже типовых звеньев и тем более их последовательных соединений могут быть построены вручную только эскизно, поскольку описываются не очень простыми выражениями. Если бы оказалось, что для анализа каких-либо свойств системы необходимо точное построение ее ЛФХ, то это свело бы на нет преимущества использования аппарата асимптотических ЛАХ. К счастью, большинство систем, с которыми приходится иметь дело, относятся к так называемым минимально-фазовым системам, для которых существует однозначная связь между амплитудной и фазовой частотными характеристиками и, следовательно, можно обойтись построением только ЛАХ — если, конечно, имеется возможность на любом этапе расчета восстановить (в случае необходимости) ЛФХ по имеющейся ЛАХ или хотя бы оценить значение фазы в любой точке ЛАХ (подробно об этом говорится в 4 2).
Таким образом, наибольшее значение для практики анапиза и синтеза автоматических систем имеет построение асимптотических ЛАХ типовых соединений звеньев. Для последовательного соединения или, что равнозначно, для передаточной функции сложного вида результирующая ЛАХ может быть найдена, как уже было сказано, простым суммированием составляющих, соответствующих передаточным функциям отдельных звеньев или сомножителям сложной передаточной функции. Однако на практике этот способ применяется редко. Более эффективной является специальная методика, позволяющая строить результирующую ЛАХ по передаточной функции сложного вида без предварительного изображения отдельных составляющих. Методика базируется том факте, что ЛАХ пропорционального, интегрирующего и дифференцирующего звеньев являются бесконечными прямыми и, следовательно, вносят свой вклад в результирующую ЛАХ во всем диапазоне частот, в то время как влияние асимптотических ЛАХ звеньев других типов начинается только с соответствующей частоты сопряжения (если рассматривать весь частотный диапазон слева направо), поскольку их низкочастотные асимптоты, если полагать коэффициент передачи этих звеньев равным единице, совпадают с осью абсцисс.
Пусть передаточная функция имеет следующий вид (или приведена к таковому):
где функция 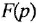
a 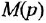
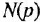
Видео:Построить структурную схему САР (САУ) по передаточной функцииСкачать

Получение структурной схемы по уравнениям
Построение структурной схемы по системе алгебраических уравнений
Пусть задана система алгебраических уравнений вида:
| 2x + 6y = 36
| 4x + 7y = 47
Выполняется преобразование схемы следующим образом. В каждом уравнении выбирается наиболее «значимая» переменная, которая остается в левой части уравнения, а всё остальное переносится в правую часть.
| 2x = 36 – 6y
| 7y = 47 – 4x
Каждое уравнение, имеющее слагаемые в правой части, на структурной схеме обозначается сумматором, на входы которого подаются слагаемые правой части с соответствующими знаками, а на выходе формируется сигнал, соответствующий левой части.
Если слагаемое правой части является свободным числом (постоянным или зависящим от времени или других переменных, не входящих в систему), то на схеме оно представляется в виде внешнего воздействия.
Если слагаемое правой части зависит от переменных системы уравнений, то эти переменные приводятся к требуемым слагаемым (например, умножаются на числа), и подключаются к сумматору.
В результате будет получена структурная схема, реализующая систему уравнений.
Построение структурной схемы по системе дифференциальных уравнений
Построение структурной схемы аналогично построению для системы алгебраических уравнений. В левой части остаются только старшие производные и вводится подстановка s = d/dt. Для получения на структурной схеме сигнала x при известном sx ставится интегратор 1/s.
Пусть задана система дифференциальных уравнений:
| x’ = x*y + 2*t
| y» = x + y — 8
В уравнениях под ‘ понимается производная первого порядка и под » — производная второго порядка. Тогда путем замены ‘ на s и, соответственно, » на s 2 получим:
| sx = x*y + 2*t
| s 2 y = x + y — 8
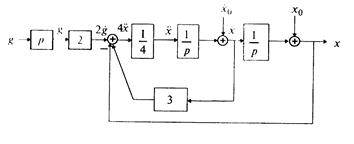
Далее на схему ставится 2 сумматора, на выходе которых формируются sx и s 2 y. Далее выход сумматора подключается к интегратору 1/s, в результате будет уже получены сигналы x и sy, и далее к выходу интегратора подключается ещё один интегратор, на выходе которого формируются уже сама переменная y. Далее эти переменные через коэффициенты усиления и блок умножения X подключаются к сумматорам. Кроме того, к сумматорам подключаются внешние воздействия 2*t и -8.
Структурная схема имеет следующий вид.
🎥 Видео
Логические выражения, таблицы истинности ,структурная логическая схемаСкачать

18) ТАУ для чайников Части 5.1 и 5.2 Структурные схемы: Условные обозначения; Правила преобразованияСкачать

Построение схем по логическим выражениямСкачать

Построение логических схемСкачать

Теория автоматического управления. Лекция 6. Структурные схемы САУСкачать
Блок-схемы для начинающих (Блок схемы алгоритмов)Скачать

Преобразование структурных схем систем управленияСкачать

c04 5, Динамические звенья 2: структурные схемыСкачать

Разбор построение логических схемСкачать
Структурная схема трехмассовой системы.Скачать

20) СТРУКТУРНЫЕ СХЕМЫ: ТИПОВАЯ ОДНОКОНТУРНАЯ СИСТЕМА.Скачать

№10. Структурные схемы, уравнения и частотные характеристики стационарных линейных систем.Скачать

23) Построение Л.А.Ч.Х. и Л.Ф.Ч.Х. системы по её передаточной функцииСкачать

8 класс. Логические элементыСкачать

Структурные схемы 2. Преобразование структурных схем 1Скачать

Составление формул органических соединений по названиюСкачать

7) ТАУ для чайников.Части 3.4 и 3.5 : Передаточная функция. Преобразование Лапласа...Скачать

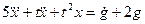
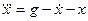


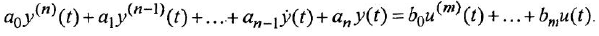
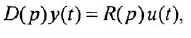
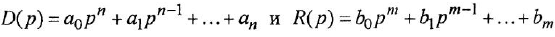
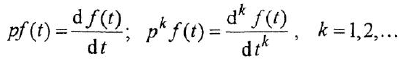
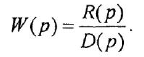
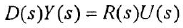
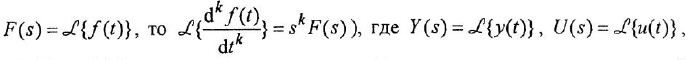
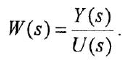
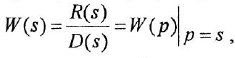
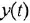 и
и 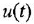 на
на 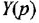 и
и 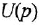 .
.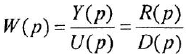 .
.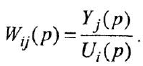
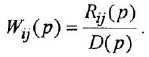
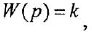
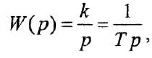
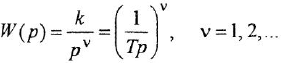
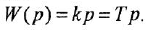
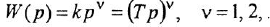
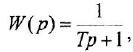
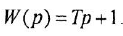
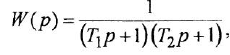
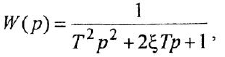
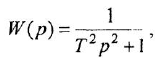
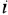 -го звена) выразить выходную переменную
-го звена) выразить выходную переменную 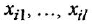 (
(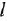 — число входов):
— число входов):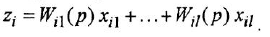
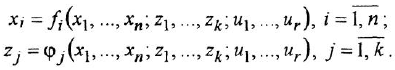
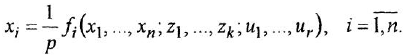
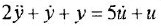
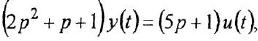
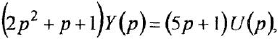
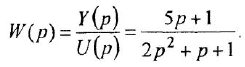
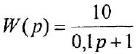
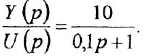
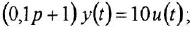
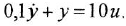
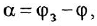
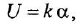
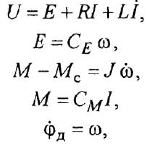
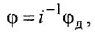
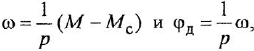
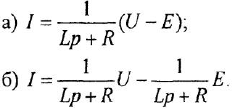
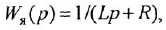
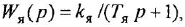
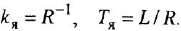
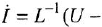
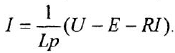
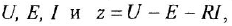
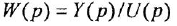
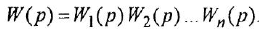
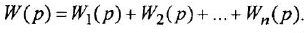
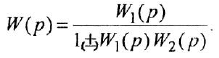
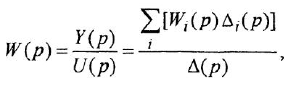
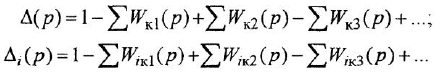
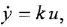 , то из
, то из 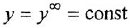 (индекс
(индекс 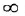 служит обозначением установившегося режима) следует, что
служит обозначением установившегося режима) следует, что 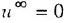 . Таким образом, в асимптотически устойчивой системе с постоянными внешними воздействиями входные переменные всех интегрирующих звеньев в установитиемся режиме равны нулю.
. Таким образом, в асимптотически устойчивой системе с постоянными внешними воздействиями входные переменные всех интегрирующих звеньев в установитиемся режиме равны нулю.