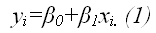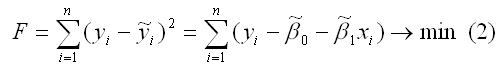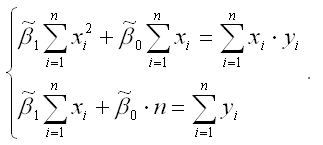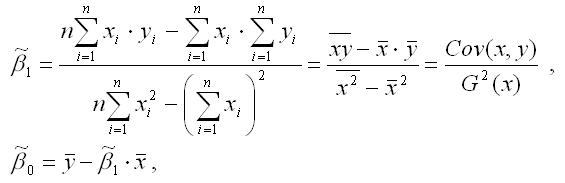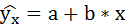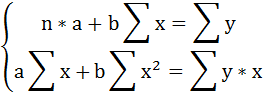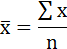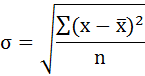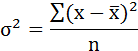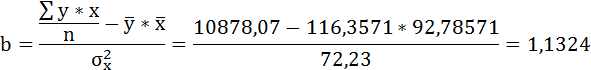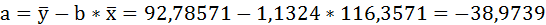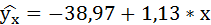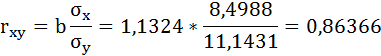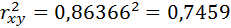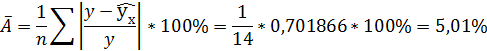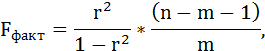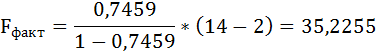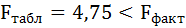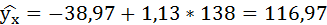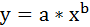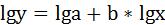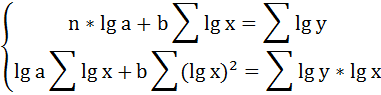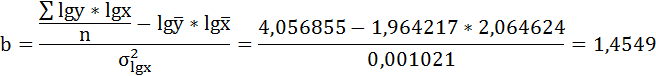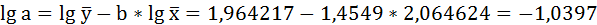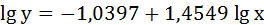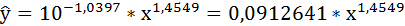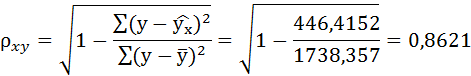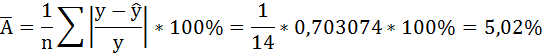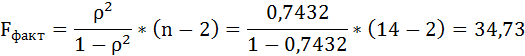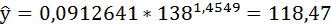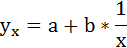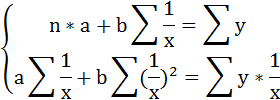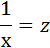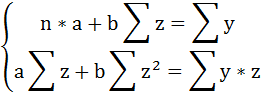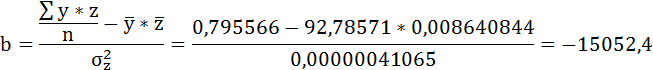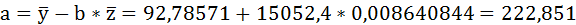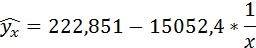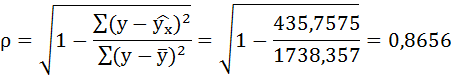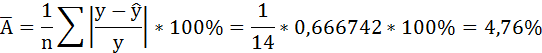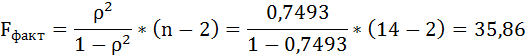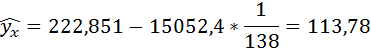Как построить систему нормальных уравнений (7 видео)

Содержание

Система нормальных уравнений и явный вид ее решения при оценивании методом наименьших квадратов линейной модели парной регрессии
Построение системы нормальных уравнений. Оценка коэффициентов уравнения множественной регрессии
Задача №1 Построение уравнения регрессии
Требуется:
Решение:
🔥 Видео

Видео:Метод наименьших квадратов. Линейная аппроксимацияСкачать

Система нормальных уравнений и явный вид ее решения при оценивании методом наименьших квадратов линейной модели парной регрессии

Предположим, что в ходе регрессионного анализа была установлена линейная взаимосвязь между исследуемыми переменными х и у, которая описывается моделью регрессии вида:

В результате оценивания данной эконометрической модели определяются оценки неизвестных коэффициентов. Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК).

Метод наименьших квадратов позволяет получить такие оценки параметров β₀и β₁, при которых сумма квадратов отклонений фактических значений результативного признака y от расчетных (теоретических) y˜ минимальна:

В процессе минимизации функции (1) неизвестными являются только значения коэффициентов β₀ и β₁, потому что значения результативной и факторной переменных известны из наблюдений. Для определения минимума функции двух переменных вычисляются частные производные этой функции по каждому из оцениваемых параметров и приравниваются к нулю. Результатом данной процедуры будет стационарная система уравнений для функции (2):

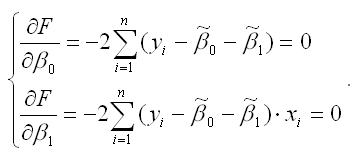
Если разделить обе части каждого уравнения системы на (-2), раскрыть скобки и привести подобные члены, то получим систему нормальных уравнений для функции регрессии вида yi=β₀+β₁xi:

Если решить данную систему нормальных уравнений, то мы получим искомые оценки неизвестных коэффициентов модели регрессии β₀ и β₁:

y – среднее значение зависимой переменной;

x – среднее значение независимой переменной;

xy – среднее арифметическое значение произведения зависимой и независимой переменных;

G 2 (x) – дисперсия независимой переменной;

Gcov (x, y) – ковариация между зависимой и независимой переменными.

Таким образом, явный вид решения системы нормальных уравнений может быть записан следующим образом:

Видео:Система уравнений. Метод алгебраического сложенияСкачать

Построение системы нормальных уравнений. Оценка коэффициентов уравнения множественной регрессии

Оцененное уравнение в первую очередь должно описывать общий тренд (направление) изменения зависимой переменной Y. При этом необходимо иметь возможность рассчитать отклонения от этого тренда.

По данным выборки объема n: (x₁_i, x₂_i, . х_pi, у_i), i = 1,2, . n, требуется оценить значения параметров b_i вектора b, т.е. оценить (приблизить) значения коэффициентов выбранной обычно вначале линейной модели (здесь х_ij, (j = 1, 2, . n) — это значение переменной X_i в j-ом наблюдении).

При выполнении предпосылок МНК (о них мы поговорим позже) относительно ошибок е_i оценки b₀, b₁, …, b_p коэффициентов b₀, b₁, . b_p множественной линейной регрессии по МНК являются несмещенными, эффективными и состоятельными.

На основании (5.2) отклонение e_i значения у_i зависимой переменной Y от теоретического (модельного) значения

соответствующего уравнению регрессии в i-м наблюдении (i = 1, 2, . n), рассчитывается по формуле

Параметры уравнения множественной регрессии оцениваются, как и в парной регрессии, методом наименьших квадратов (МНК), т.е. минимизируется функция S(b₀, b₁,…, b_p) по переменным b₀, b₁,…, b_p

S(b₀, b₁,…, b_p) = . (5.3′)

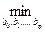
На основании необходимого условия экстремума функции многих переменных S(b₀, b₁. b_p), представляющей (5.3′), необходимо приравнять к нулю частные производные по этим переменным или в матричной форме — вектор частных производных

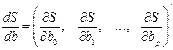
В результате получится система p+1 линейных уравнений для неизвестных b₀, b₁. b_p. После приведения подобных членов получится система нормальных уравнений, решение которой и позволяет получить оценку коэффициентов множественной регрессии.

Ее решение может быть найдено в частности, методом Гаусса, методом Крамера, методом вычисления обратной матрицы и многими другими методами решения систем линейных уравнений.

В пункте 5.3 будет показано, как обратиться к процедурам в Microsoft Excel, позволяющим решать это уравнение и вычислять не только значения коэффициентов множественной регрессии, но и числовые значения других ее характеристик.

При нелинейной зависимости признаков, приводимой к линейному виду, значения коэффициентов множественной регрессии также определяются также с помощью метода наименьших квадратов лишь с той разницей, что он применяется не к исходной информации, а к преобразованным данным. Так, рассматривая степенную функцию

мы преобразовываем её в линейный вид:

где переменные выражены в логарифмах.

Далее метод наименьших квадратов применяется так же, как и раньше: строится система нормальных уравнений и определяются значения ln(a), b1, b2, …, bp. Потенцируя ln(a), найдём значение параметра а и общий вид уравнения степенной функции.

Поскольку параметры степенной функции представляют собой коэффициенты эластичности, то они сравнимы по разным факторам.

Пример 2. При исследовании спроса на некоторый продукт получено следующее уравнение

где у – количество продукта на душу населения (кг); х₁ – цена (руб.); х₂ – доход на душу населения (тыс. руб.)

Из этого уравнения видно, что с ростом цены на 1% при том же доходе спрос снижается в среднем на 0,888%, а увеличение дохода на 1% при неизменных ценах вызывает увеличение спроса на 1,126%.

При других нелинейных функциях методика оценки параметров метода наименьших квадратов выполняется также. В отличие от предыдущих функций параметры более сложных моделей не имеют чёткой экономической интерпретации – они не являются показателями силы связи и её эластичности. Это не исключает возможности их применения, но делает их менее привлекательными в практических расчётах.

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Задача №1 Построение уравнения регрессии

Имеются следующие данные разных стран об индексе розничных цен на продукты питания (х) и об индексе промышленного производства (у).

Индекс розничных цен на продукты питания (х)	Индекс промышленного производства (у)
1	100	70
2	105	79
3	108	85
4	113	84
5	118	85
6	118	85
7	110	96
8	115	99
9	119	100
10	118	98
11	120	99
12	124	102
13	129	105
14	132	112

Требуется:

1. Для характеристики зависимости у от х рассчитать параметры следующих функций:

В) равносторонней гиперболы.

2. Для каждой модели рассчитать показатели: тесноты связи и среднюю ошибку аппроксимации.

3. Оценить статистическую значимость параметров регрессии и корреляции.

4. Выполнить прогноз значения индекса промышленного производства у при прогнозном значении индекса розничных цен на продукты питания х=138.

Решение:

1. Для расчёта параметров линейной регрессии

Решаем систему нормальных уравнений относительно a и b:

Построим таблицу расчётных данных, как показано в таблице 1.

Таблица 1 Расчетные данные для оценки линейной регрессии

№ п/п	х	у	ху	x 2	y 2
1	100	70	7000	10000	4900	74,26340	0,060906
2	105	79	8295	11025	6241	79,92527	0,011712
3	108	85	9180	11664	7225	83,32238	0,019737
4	113	84	9492	12769	7056	88,98425	0,059336
5	118	85	10030	13924	7225	94,64611	0,113484
6	118	85	10030	13924	7225	94,64611	0,113484
7	110	96	10560	12100	9216	85,58713	0,108467
8	115	99	11385	13225	9801	91,24900	0,078293
9	119	100	11900	14161	10000	95,77849	0,042215
10	118	98	11564	13924	9604	94,64611	0,034223
11	120	99	11880	14400	9801	96,91086	0,021102
12	124	102	12648	15376	10404	101,4404	0,005487
13	129	105	13545	16641	11025	107,1022	0,020021
14	132	112	14784	17424	12544	110,4993	0,013399
Итого:	1629	1299	152293	190557	122267	1299,001	0,701866
Среднее значение:	116,3571	92,78571	10878,07	13611,21	8733,357	х	х
	8,4988	11,1431	х	х	х	х	х
	72,23	124,17	х	х	х	х	х

Среднее значение определим по формуле:

Cреднее квадратическое отклонение рассчитаем по формуле:

и занесём полученный результат в таблицу 1.

Возведя в квадрат полученное значение получим дисперсию:

Параметры уравнения можно определить также и по формулам:

Таким образом, уравнение регрессии:

Следовательно, с увеличением индекса розничных цен на продукты питания на 1, индекс промышленного производства увеличивается в среднем на 1,13.

Рассчитаем линейный коэффициент парной корреляции:

Связь прямая, достаточно тесная.

Определим коэффициент детерминации:

Вариация результата на 74,59% объясняется вариацией фактора х.

Подставляя в уравнение регрессии фактические значения х, определим теоретические (расчётные) значения .

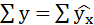
следовательно, параметры уравнения определены правильно.

Рассчитаем среднюю ошибку аппроксимации – среднее отклонение расчётных значений от фактических:

В среднем расчётные значения отклоняются от фактических на 5,01%.

Оценку качества уравнения регрессии проведём с помощью F-теста.

F-тест состоит в проверке гипотезы Н₀ о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического F_факт и критического (табличного) F_табл значений F-критерия Фишера.

F_факт определяется по формуле:

где n – число единиц совокупности;

m – число параметров при переменных х.

Таким образом, Н₀ – гипотеза о случайной природе оцениваемых характеристик отклоняется и признаётся их статистическая значимость и надёжность.

Полученные оценки уравнения регрессии позволяют использовать его для прогноза.

Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:

2. Степенная регрессия имеет вид:

Для определения параметров производят логарифмирование степенной функции:

Для определения параметров логарифмической функции строят систему нормальных уравнений по способу наименьших квадратов:

Построим таблицу расчётных данных, как показано в таблице 2.

Таблица 2 Расчетные данные для оценки степенной регрессии

№п/п	х	у	lg x	lg y	lg x*lg y	(lg x) 2	(lg y) 2
1	100	70	2,000000	1,845098	3,690196	4,000000	3,404387
2	105	79	2,021189	1,897627	3,835464	4,085206	3,600989
3	108	85	2,033424	1,929419	3,923326	4,134812	3,722657
4	113	84	2,053078	1,924279	3,950696	4,215131	3,702851
5	118	85	2,071882	1,929419	3,997528	4,292695	3,722657
6	118	85	2,071882	1,929419	3,997528	4,292695	3,722657
7	110	96	2,041393	1,982271	4,046594	4,167284	3,929399
8	115	99	2,060698	1,995635	4,112401	4,246476	3,982560
9	119	100	2,075547	2,000000	4,151094	4,307895	4,000000
10	118	98	2,071882	1,991226	4,125585	4,292695	3,964981
11	120	99	2,079181	1,995635	4,149287	4,322995	3,982560
12	124	102	2,093422	2,008600	4,204847	4,382414	4,034475
13	129	105	2,110590	2,021189	4,265901	4,454589	4,085206
14	132	112	2,120574	2,049218	4,345518	4,496834	4,199295
Итого	1629	1299	28,90474	27,49904	56,79597	59,69172	54,05467
Среднее значение	116,3571	92,78571	2,064624	1,964217	4,056855	4,263694	3,861048
	8,4988	11,1431	0,031945	0,053853	х	х	х
	72,23	124,17	0,001021	0,0029	х	х	х

Продолжение таблицы 2 Расчетные данные для оценки степенной регрессии

№п/п	х	у
1	100	70	74,16448	17,34292	0,059493	519,1886
2	105	79	79,62057	0,385112	0,007855	190,0458
3	108	85	82,95180	4,195133	0,024096	60,61728
4	113	84	88,59768	21,13866	0,054734	77,1887
5	118	85	94,35840	87,57961	0,110099	60,61728
6	118	85	94,35840	87,57961	0,110099	60,61728
7	110	96	85,19619	116,7223	0,11254	10,33166
8	115	99	90,88834	65,79901	0,081936	38,6174
9	119	100	95,52408	20,03384	0,044759	52,04598
10	118	98	94,35840	13,26127	0,037159	27,18882
11	120	99	96,69423	5,316563	0,023291	38,6174
12	124	102	101,4191	0,337467	0,005695	84,90314
13	129	105	107,4232	5,872099	0,023078	149,1889
14	132	112	111,0772	0,85163	0,00824	369,1889
Итого	1629	1299	1296,632	446,4152	0,703074	1738,357
Среднее значение	116,3571	92,78571	х	х	х	х
	8,4988	11,1431	х	х	х	х
	72,23	124,17	х	х	х	х

Решая систему нормальных уравнений, определяем параметры логарифмической функции.

Получим линейное уравнение:

Выполнив его потенцирование, получим:

Подставляя в данное уравнение фактические значения х, получаем теоретические значения результата 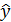. По ним рассчитаем показатели: тесноты связи – индекс корреляции и среднюю ошибку аппроксимации.

Связь достаточно тесная.

В среднем расчётные значения отклоняются от фактических на 5,02%.

Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:

3. Уравнение равносторонней гиперболы

Для определения параметров этого уравнения используется система нормальных уравнений:

Произведем замену переменных

и получим следующую систему нормальных уравнений:

Решая систему нормальных уравнений, определяем параметры гиперболы.

Составим таблицу расчётных данных, как показано в таблице 3.

Таблица 3 Расчетные данные для оценки гиперболической зависимости

№п/п	х	у	z	yz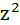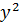
1	100	70	0,010000000	0,700000	0,0001000	4900
2	105	79	0,009523810	0,752381	0,0000907	6241
3	108	85	0,009259259	0,787037	0,0000857	7225
4	113	84	0,008849558	0,743363	0,0000783	7056
5	118	85	0,008474576	0,720339	0,0000718	7225
6	118	85	0,008474576	0,720339	0,0000718	7225
7	110	96	0,009090909	0,872727	0,0000826	9216
8	115	99	0,008695652	0,860870	0,0000756	9801
9	119	100	0,008403361	0,840336	0,0000706	10000
10	118	98	0,008474576	0,830508	0,0000718	9604
11	120	99	0,008333333	0,825000	0,0000694	9801
12	124	102	0,008064516	0,822581	0,0000650	10404
13	129	105	0,007751938	0,813953	0,0000601	11025
14	132	112	0,007575758	0,848485	0,0000574	12544
Итого:	1629	1299	0,120971823	11,13792	0,0010510	122267
Среднее значение:	116,3571	92,78571	0,008640844	0,795566	0,0000751	8733,357
	8,4988	11,1431	0,000640820	х	х	х
	72,23	124,17	0,000000411	х	х	х

Продолжение таблицы 3 Расчетные данные для оценки гиперболической зависимости

№п/п	х	у
1	100	70	72,3262	0,033231	5,411206	519,1886
2	105	79	79,49405	0,006254	0,244083	190,0458
3	108	85	83,47619	0,017927	2,322012	60,61728
4	113	84	89,64321	0,067181	31,84585	77,1887
5	118	85	95,28761	0,121031	105,8349	60,61728
6	118	85	95,28761	0,121031	105,8349	60,61728
7	110	96	86,01027	0,10406	99,79465	10,33166
8	115	99	91,95987	0,071112	49,56344	38,6174
9	119	100	96,35957	0,036404	13,25272	52,04598
10	118	98	95,28761	0,027677	7,357059	27,18882
11	120	99	97,41367	0,016024	2,516453	38,6174
12	124	102	101,46	0,005294	0,291565	84,90314
13	129	105	106,1651	0,011096	1,357478	149,1889
14	132	112	108,8171	0,028419	10,1311	369,1889
Итого:	1629	1299	1298,988	0,666742	435,7575	1738,357
Среднее значение:	116,3571	92,78571	х	х	х	х
	8,4988	11,1431	х	х	х	х
	72,23	124,17	х	х	х	х

Значения параметров регрессии a и b составили:

Связь достаточно тесная.

В среднем расчётные значения отклоняются от фактических на 4,76%.

По уравнению равносторонней гиперболы получена наибольшая оценка тесноты связи по сравнению с линейной и степенной регрессиями. Средняя ошибка аппроксимации остаётся на допустимом уровне.