Как построить плоскость в матлабе по уравнению (8 видео)

Построение трехмерных графиков в MATLAB

Построение трехмерных графиков в MATLAB.

График функции двух переменных в MATLAB – это поверхность, расположенная над областями определения функции. Поэтому для прорисовки такого графика требуется использование трехмерного изображения.

Простейшим инструментом, способным отобразить график функции дыух переменных, является

plot3( X, Y, Z )

где X, Y и Z – матрицы со значениями функции (точками z) в наборах (x, y).

В системе MATLAB имеется специальная функция для получения двумерных массивов X и Y по одномерным массивам x, y.

В MATLAB существует функция построения двумерных массивов X и Y по одномерным x, y.

Пусть по оси x задан вектор

u = -2 : 0.1 : 2 ,

а по оси y диапазон

Для получения матриц X и Y, содержащих значения точек в этой прямоугольной сетке, используется функция:

[ X, Y ] = meshgrid( u, v )

Вычислим теперь на полученной прямоугольной сетке значение функции exp:

Z = exp( — X.^2 — Y.^2 )

Теперь применим функцию plot3, которая была описана выше, и получим следующий график:

Чтобы построить трехмерные линии, заданные параметрически, применяется другая форма вызова функции plot3:

plot3( x, y, z )

здесь x, y и z — одномерные массивы координат точек, которые надо последовательно соединить отрезками прямых.

Следующий пример позволяет построить винтовую линию:

t = 0 : pi/50 : 10*pi ;

x = sin( t );

y = cos( t );

plot3( x, y, t );

grid on

Причем следует отметить, что функции по обработке графиков, допустимые в двумерном случае, работают и для трехмерных изображений.

Кроме этой простейшей функции построения графиков в MATLAB есть набор инструментов, позволяющий сделать отображаемые объекты более наглядными. Это функции mesh, surf и surfl.

Функция mesh соединяет вычисленные соседние точки поверхности графика отрезками прямых и показывает в графическом окне системы MATLAB плоскую проекцию такого объёмного «каркасно-ребристого» ( по-английски зовётся wireframe mesh) тела. Вместо ранее показанного при помощи функции plot3 графика функции

Mesh соединяет соседние вычислительные точки отрезками, причем невидимые линии при отображении скрываются. Если же такие линии для отображения необходимы, нужно воспользоваться командой.

Для примера рассмотрим использование функции mesh в случае построения того же графика функции

exp( — X.^2 — Y.^2 )

Вызов же функции

позволяет получить следующее изображение, представляющее собой поверхность, а не набор линий.

Раскрашивание отдельных элементов поверхности в этом случае производится автоматически. Если же раскрасить их необходимо по-другому, лучше всего воспользоваться функцией surfl.

Эта функция воспринимает построенную поверхность как материальную, обладающую определенными свойствами. По умолчанию она задает некоторый источник света, после чего рассчитывает траектории отраженных от поверхности лучей. Таким образом, если задать условные параметры материала поверхности, например:

colormap( copper ) ,

то есть набор цветов (colormap), соответствующий меди (copper), то после вызова функции

surfl( X, Y, Z )

мы получим следующий график:

Убрать черные линии и добиться более лпавного света позволяет команда

Содержание

Построение плоскости на основе нормального вектора и точки в Matlab или matplotlib
5 ответов
Построение графиков поверхностей, заданных параметрически
🔍 Видео

Видео:MATLAB 07 Интерактивное построение графиковСкачать

Построение плоскости на основе нормального вектора и точки в Matlab или matplotlib

Как можно построить плоскость в matlab или matplotlib из нормального вектора и точки?

Видео:Как в MATLAB Simulink моделировать уравнения (Структурная схема САУ)Скачать

5 ответов

Примечание: это решение работает только до тех пор, пока normal(3) не равен 0. Если плоскость параллельна оси z, вы можете повернуть размеры, чтобы сохранить тот же подход:

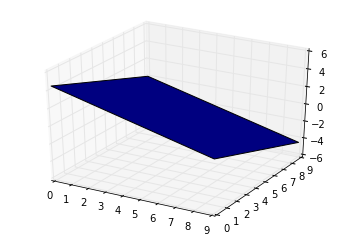
для всех копий / пастеров там, вот аналогичный код для Python с использованием matplotlib:

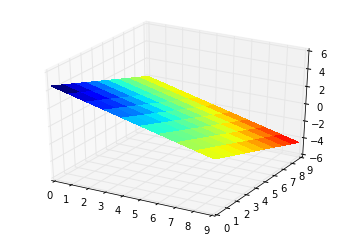
для копировальных пастеров, желающих градиент на поверхности:

приведенные выше ответы достаточно хороши. Следует отметить, что они используют тот же метод,который вычисляет значение z для данного (x, y). Обратная сторона заключается в том, что они мешгрид плоскости и плоскости в пространстве могут меняться (только сохраняя свою проекцию одинаковой). Например, вы не можете получить квадрат в 3D-пространстве (но искаженный).

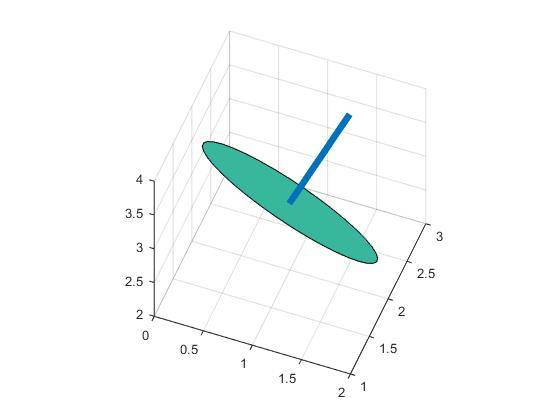
чтобы избежать этого, есть и другой способ, с помощью вращения. Если вы сначала генерируете данные в плоскости x-y (может быть любой формы), затем поверните его равное количество ([0 0 1] к вашему вектору), тогда вы получите то, что хотите. Просто запустите ниже код для справки.

он получает круг в 3D:

более чистый пример Python, который также работает для сложных ситуаций $z,y,z$,

Видео:Плоскость в пространстве через 3 точки в MatlabСкачать

Построение графиков поверхностей, заданных параметрически

ГРАФИКИ В MATLAB. ПОСТРОЕНИЕ ТРЕХМЕРНЫХ ГРАФИКОВ

Цель работы: приобрести навыки построения трехмерных графиков в MatLab.

График поверхности (трехмерный или 3D-график) – это график, положение точки в котором определяется значениями трех координат.

Построение графиков поверхностей

Декартовая система координат состоит из заданной фиксированной точкой пространства О, называемой началом координат, и трех перпендикулярных прямых пространства ОХ, OY, OZ, не лежащих в одной плоскости и пересекающихся в начале координат – их называют координатными осями (ОХ – ось абсцисс, OY – ось ординат, OZ – ось аппликат). Положение точки М в пространственной системе координат определяется значением трех координат и обозначается М(х,у,z). Три плоскости, содержащие пары координатных осей, называются координатными плоскостями XY, XZ, YZ.

Величина z называется функцией двух переменных х и у, если каждой паре чисел, которые могут быть значениями переменных х и у, соответствует одно или несколько определенных значений величины z. При этом переменные хи у называют аргументами функции z(x, у).Пары тех чисел, которые могут быть значениями аргументов х, у функции z(x, у),в совокупности составляют область onределения функции.

Для построения графика двух переменных z=f(x,y) необходимо выполнить следующие действия:

1. Сформировать в области построения графика прямоугольную сетку, проводя прямые, параллельные осям y=y_j и x=x_i, где x_i=x₀+ih, h=(x_n-x_o)/k, i=0,1,2,…,n, .

2. Вычислить значения 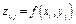во всех узлах сетки.

3. Обратится к функции построения поверхности, передавая ей в качестве параметров сетку и матрицу Z=(z_i,j) значений в узлах сетки.

Функцияmeshgrid – для форматирования прямоугольной сетки.

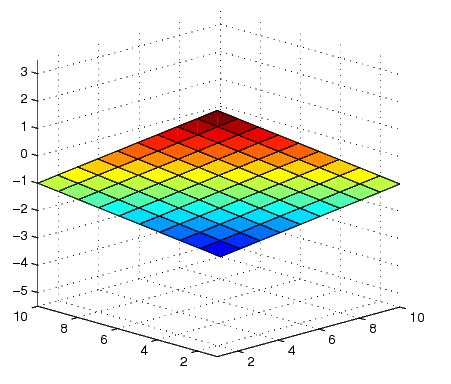
ПРИМЕР 1 Построить график функции z(x,y)=y 2 -x 2 , где х [2,2], y [-3,3].

Для форматирования сетки воспользуемся функцией meshgrid.

После формирования сетки вычислим значение z во всех узлах.

Обратимся к функции mesh для построения графика: mesh(x,y).

В результате чего будет построен трехмерный график (рис. 1).

Для получения менее грубого графика следует сетку делать более плотной (рис. 2).

Рис. 1График функции z(x,y) = y 2 — x 2

Рис. 2График функции z(x,y) = y 2 — x 2 с плотной сеткой

Функция surf – строит каркасную поверхность, заливая каждую ее клетку цветом, который зависит от значения функции в узлах сетки.

ПРИМЕР 2

Построить график функции .

Рис. 3График функции

В MatLab можно построить графики двух поверхностей в одной системе координат. Для этого, как и для плоских графиков, следует использовать команду hold on, которая блокирует создание второго нового окна при выполнении команд surfили mesh.

ПРИМЕР 3

Построить график функции z(x, у) = ±(х 2 + y 2 ) — 1.

Рис. 4График функции z(x, у) = ±(х 2 + y 2 ) — 1

Построение графиков поверхностей, заданных параметрически

При построении графиков поверхностей, заданных параметрически: х(u, v), у(u, v) и z(u, v), необходимо построить матрицы X, Y и Z одинакового размера. Для этого массивы u и v должны быть одинакового размера. После этого следует выделить два основных вида представления х, у и z в случае параметрического задания поверхностей:

1. Если х, у и z представимы в виде f(u)*g(u), то соответствующие им матрицы X, Y и Z следует формировать в виде матричного умножения f(u) на g(u).

2. Если х, у и z представимы в виде f(u) или g(u), то в этом случае матрицы X, Y и Z следует записывать в виде f(u)ones(size(v)) или g(u)ones(size(u)) соответственно.

ПРИМЕР 4

Построить поверхность однополостного гиперболоида, уравнение которого задано в параметрическом виде:

%Формируем матрицу X как матричное произведение ch(u)*cos(v)

%Формируем матрицу Y как матричное произведение ch(u)*sin(v)

%Формируем матрицу Z как матричное произведение столбца sh(u) на строку

%Формируем график поверхности

%Подписываем график и оси

title(‘ГРАФИК ОДНОПОЛОСТНОГО ГИПЕРБОЛОИДА’);

Общие принципы форматирования трехмерных графиков остаются теми же, что и в двумерном случае.

Анимация

При изучении движения точки на плоскости и в пространстве, MatLab позволит построить график движения и проследить за ним. Для построения анимационного ролика в MatLab существуют две функции: comet(х, у) и comet3(х,y,z). Функция comet(х, у) позволит увидеть движение точки вдоль кривой у(х) на плоскости, а функция comet3(х, у, z)позволит проследить за ее движением вдоль пространственной кривой z(x, у).

ПРИМЕР 5

Движение точки на плоскости вдоль эллипса, который параметрически задается уравнением .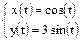

ПРИМЕР 6

Движение точки в пространстве вдоль винтовой линии, параметрическое уравнение которой имеет вид .

1. Построить графики поверхностей, заданных явно и параметрически; использовать встроенную функцию MatLab figure(n) для размещения программного кода в одном программном окне (a, p – номер компьютера; b,q – номер в списке группы; с – произвольное число).

2. Создать анимационный ролик, использовав при этом две любые функции из приведенных ниже.