Как построить плоскость по уравнению (3 видео)

5.1.4. Как построить плоскость?

Несмотря на обилие программ и онлайн сервисов, ручное построение чертежей сохранит актуальность и через много лет, хотя бы потому, что позволит учащимся качественно усвоить материал. Что нужно знать и уметь в самых суровых условиях?

Прежде всего, вы должны на полном автомате узнавать уравнения плоскостей, которые параллельны координатным плоскостям . Фрагменты плоскостей стандартно обозначают прямоугольниками, которые в последних двух случаях выглядят, как параллелограммы. Размеры выбираем разумные, при этом желательно, чтобы точка, в которой координатная ось «протыкает» плоскость являлась центром симметрии:

Повторим заодно и неравенства:

– неравенство (левый чертёж) задаёт дальнее от нас полупространство, исключая саму плоскость ;
– неравенство (чертёж посередине) задаёт правое полупространство, включая плоскость ;
– двойное неравенство (правый чертёж) задаёт «слой», расположенный между плоскостями , включая обе плоскости.

Задача 124

Изобразить тело, ограниченное плоскостями , составить систему неравенств, определяющих данное тело.

Это задание для самостоятельного решения. Из-под грифеля вашего карандаша должен выйти старый знакомый прямоугольный параллелепипед. Не забывайте, что невидимые рёбра и грани следует прочертить пунктиром. Готовый чертёж в конце книги.

НЕ ПРЕНЕБРЕГАЙТЕ учебными задачами!
Особенно, если они кажутся простыми

А то может статься, раз пропустили, два пропустили, а затем потратили битый час, вымучивая трёхмерный чертёж в каком-нибудь реальном примере. Причём, несложный.

Следующую группу плоскостей условно назовём «прямыми пропорциональностями» – это плоскости, проходящие через координатные оси:

1) уравнение вида (здесь и далее ) задаёт плоскость, проходящую через ось ;
2) уравнение вида задаёт плоскость, проходящую через ось ;
3) уравнение вида задаёт плоскость, проходящую через ось .

Задача 125

Построить плоскость

Как лучше осуществить построение? Предлагаю следующий алгоритм:

Сначала перепишем уравнение в виде , из которого хорошо видно, что «игрек» может принимать любые значения. Зафиксируем значение , то есть, будем рассматривать координатную плоскость . Уравнения задают пространственную прямую, лежащую в этой плоскости. Данная прямая проходит через начало координат, поэтому для её построения достаточно найти одну точку. Пусть . Откладываем точку и проводим прямую:

Теперь возвращаемся к уравнению плоскости . Поскольку «игрек» принимает любые значения, то построенная в плоскости прямая непрерывно «тиражируется» влево и вправо. Именно так и образуется наша плоскость , проходящая через ось . Чтобы завершить чертёж, слева и справа от прямой откладываем две параллельные линии и поперечными горизонтальными отрезками «замыкаем» символический параллелограмм.

И ещё раз повторим смысл пространственного линейного неравенства на примере . Как определить полупространство, которое оно задаёт? Берём какую-нибудь точку, не принадлежащую плоскости , например, точку из ближнего к нам полупространства и подставляем её координаты в неравенство:
– получено верное неравенство, значит, неравенство задаёт нижнее (относительно плоскости ) полупространство, при этом сама плоскость не входит в решение.

Задача 126

Построить плоскости
а) , б) .

Это задания для самостоятельного решения, в случае затруднений используйте аналогичные рассуждения. Краткие указания и чертежи в конце книги.

На практике особенно распространены плоскости, параллельные оси . Частный случай, когда плоскость проходит через ось, только что был в пункте «бэ», и сейчас мы разберём более общую задачу:

Задача 127

Построить плоскость

Решение: в уравнение в явном виде не участвует переменная «зет», а значит, плоскость параллельна оси аппликат. Применим ту же технику, что и в предыдущих примерах.

Перепишем уравнение плоскости в виде , из которого понятно, что «зет» может принимать любые значения. Зафиксируем и в «родной» плоскости начертим обычную «плоскую» прямую . Для её построения удобно взять опорные точки .

Поскольку «зет» принимает все значения, то построенная прямая непрерывно «размножается» вверх и вниз, образуя тем самым искомую плоскость . Аккуратно оформляем параллелограмм разумной величины.

Содержание

Уравнение плоскости в отрезках: описание, примеры, решение задач
Уравнение плоскости в отрезках – описание и примеры
Приведение общего уравнения плоскости к уравнению плоскости в отрезках
Лекция Плоскость
📽️ Видео

Видео:Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать

Уравнение плоскости в отрезках: описание, примеры, решение задач

Данный раздел будет полностью посвящен теме «Уравнение плоскости в отрезках». Мы последовательно рассмотрим, какой вид имеет уравнение плоскости в отрезках, применение этого уравнения для построения заданной плоскости в прямоугольной системе координат, переход от общего уравнения плоскости к уравнению плоскости в отрезках. В статье мы рассмотрим большое количество примеров, которые облегчат усвоение информации.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Уравнение плоскости в отрезках – описание и примеры

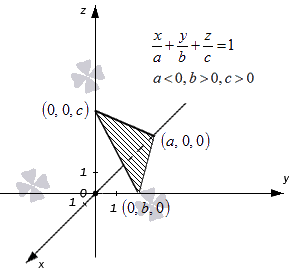
Уравнение плоскости в отрезках имеет вид x a + y b + z c = 1 , где a , b и c – это действительные числа, отличные от нуля. Абсолютные величины чисел a , b и c равны длинам отрезков, которые отсекаются плоскостью на осях координат O х , O у и O z в трехмерной системе координат O х у z . Откладываются длины отрезков от начала координат. Направление, в котором необходимо отложить длину отрезка, определяет знак, стоящий перед числом. Наличие «-» свидетельствует о том, что отрезок надо откладывать от нуля в отрицательном направлении оси.

Действительно, координаты точек a , 0 , 0 , 0 , b , 0 , 0 , 0 , c удовлетворяют уравнению плоскости в отрезках:

a a + 0 b + 0 c = 1 = 1 ⇔ 1 = 1 0 a + b b + 0 c = 1 = 1 ⇔ 1 = 1 0 a + 0 b + c c = 1 = 1 ⇔ 1 = 1

Поясним этот момент, расположив заданные точки на графике.

Проиллюстрируем описанное выше примером.

Плоскость проходит через точки — 2 , 0 , 0 , 0 , 3 , 0 и 0 , 0 , — 1 2 на осях координат в прямоугольной системе координат O x y z . Необходимо записать уравнение плоскости в отрезках.

Решение

Определим положение отрезков, отсекаемых плоскостью на осях координат. На оси абсцисс откладываем в отрицательном направлении отрезок длиной 2 единицы. На оси ординат в положительном направлении откладываем отрезок длиной 3 . На оси аппликат в отрицательном направлении откладываем отрезок длиной 1 2 .

При этом, уравнение плоскости в отрезках будет иметь вид: x — 2 + y 3 + z — 1 2 = 1 .

Ответ: x — 2 + y 3 + z — 1 2 = 1

Уравнение плоскости в отрезках удобно использовать для построения чертежей. Проиллюстрируем это утверждение примером.

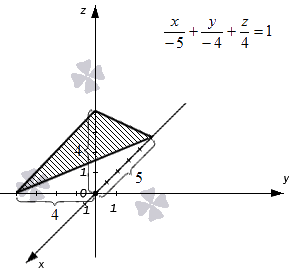
Плоскость в прямоугольной системе координат O х у z задана уравнением плоскости в отрезках вида x — 5 + y — 4 + z 4 = 1 . Необходимо изобразить эту плоскость на графике.

Решение

Изобразим оси координат, обозначаем начало координат и единичные отрезки на осях. Отмечаем длины отрезков, отсекаемых плоскостью, на каждой из осей. Соединяем концевые точки отрезков прямыми линиями. Полученная плоскость имеет вид треугольника. Она соответствует заданному уравнению плоскости в отрезках x — 5 + y — 4 + z 4 = 1 .

Ответ:

Плоскость может быть задана уравнением плоскости другого вида. Для того, чтобы изобразить заданную плоскость на чертеже, можно сначала перейти к уравнению плоскости в отрезках. Получив уравнение плоскости в отрезках, нам останется лишь отметить точки a , 0 , 0 , 0 , b , 0 , 0 , 0 , c и соединить их прямыми линиями.

Видео:1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Приведение общего уравнения плоскости к уравнению плоскости в отрезках

Мы имеем общее уравнение плоскости в пространстве вида A x + B y + C z + D = 0 . И мы можем получить уравнение плоскости в отрезках. Сделать это можно в том случае, если плоскость пересекает все координатные оси, причем не в начале координат.

Не получится перевести общее уравнение плоскости в пространстве в уравнение плоскости в отрезках в тех случаях, когда плоскость проходит через одну из координатных осей или располагается параллельно оси. Другими словами, мы можем работать лишь с полным уравнением плоскости вида A x + B y + C z + D = 0 , где A ≠ 0 , B ≠ 0 , C ≠ 0 , D ≠ 0 .

Приведение общего уравнения плоскости к уравнению плоскости в пространстве производится следующим образом. Переносим слагаемое D в правую часть уравнения с противоположным знаком.

A x + B y + C z + D = 0 ⇔ A x + B y + C z = — D

Так как D ≠ 0 , то обе части полученного уравнения можно разделить на – D : A — D x + B — D y + C — D z = 1 .

Так как A ≠ 0 , B ≠ 0 , C ≠ 0 , то мы можем отправить в знаменатели коэффициенты перед переменными x , y и z . Последнее уравнение эквивалентно равенству x — D A + y — D B + z — D C = 1 . При этом мы использовали очевидное равенство p q = 1 q p , p , q ∈ R , p ≠ 0 , q ≠ 0 .

В итоге, мы получаем уравнение плоскости в отрезках. Это становится хорошо видно в том случае, если обозначить — D A = a , — D B = b , — D C = c .

Разберем решение примера.

Плоскость в прямоугольной системе координат O x y z в пространстве задана уравнением вида 3 x + 9 y — 6 z — 6 = 0 . Переведем это уравнение в уравнение плоскости в отрезках.

Решение

Данное в условии задачи уравнение является полным уравнением плоскости. Это дает нам возможность привески его к уравнению плоскости в отрезках. Перенесем — 6 в правую часть равенства, а затем разделим обе части равенства на 6 :

3 x + 9 y — 6 z — 6 = 0 ⇔ 3 x + 9 y + 6 z = 6 3 x + 9 y — 6 z = 6 ⇔ 1 2 x + 3 2 y — z = 1

Коэффициенты при переменных x, y и z отправим в знаменатели: 1 2 x + 3 2 y — z = 1 ⇔ x 2 + y 2 3 + z — 1 = 1 . Полученное уравнение и есть уравнение плоскости в отрезках.

Ответ: x 2 + y 2 3 + z — 1 = 1

Видео:10. Параллельность и перпендикулярность плоскостей Решение задачСкачать

Лекция Плоскость

Лекция № 10. Тема 4 : Плоскость

4.1. Уравнение плоскости. Построение плоскости

Теорема. В ДСК в пространстве каждая плоскость может быть задана линейным уравнением и наоборот, т. е. любое линейное уравнение в ДСК в пространстве определяет плоскость.

Доказательство этой теоремы полностью аналогично доказательству теоремы о прямой линии в ДСК на плоскости.

Уравнение называется общим уравнением плоскости .

Замечание 1. Аналогично следует, что вектор является нор-мальным вектором плоскости.

Пример 1. Составить уравнение плоскости, параллельной плоскости О yz .

Поскольку в этом случае , то уравнение искомой плоскости будет иметь следующий вид .

Удобно и наглядно строить плоскость по её следам на координатных плоскостях, которые определяются из следующих систем уравнений:

Пример 2. Построить z

плоскость, заданную общим

уравнением

Определим координаты 0 2 y

точек пересечения с осями 1

координат : ( 1 , 0 , 0 ) , ( 0 , 2 , 0 )

и ( 0 , 0 ,  2 ) и соединим эти x  2

Замечание 2. По следам плоскость удобно строить, представив уравнение плоскости в виде

Это уравнение называется уравнением плоскости в отрезках , так как  отрезки, отсекаемые плоскостью на координатных осях.

4.2. Уравнение плоскости, проходящей через заданную точку, перпендикулярно заданному вектору

Пусть требуется составить уравнение плоскости, проходящей через точку перпендикулярно вектору . Пусть точка  текущая точка плоскости. Тогда вектор , лежащий на плоскости, перпендикулярен вектору

Таким образом, из этого условия получаем

(1)

Уравнение (1) является искомым уравнением плоскости.

Пример 3. Составить уравнение плоскости, проходящей через ось

В этом случае вектор нормали к плоскости а в качестве точки выберем начало координат. Тогда из уравнения (1) имеем

4.3. Уравнение плоскости, проходящей через три заданные точки

Т ребуется составить уравнение плоскости, проходящей через три точки

Пусть точка  текущая

точка плоскости. Построим векторы

. Они компланарны,

т.е. их смешанное произведение

или

(2)

Пример 4. Составить уравнение плоскости, проходящей через начало координат и точки

Из уравнения (2) получим

4.4. Угол между двумя плоскостями

Пусть две плоскости заданы общими уравнениями

Очевидно, угол между двумя

плоскостями равен углу между их

Из этого следует

(3)

Если плоскости перпендикулярны, то

Если плоскости параллельны, то их нормальные векторы коллинеарны и тогда условие параллельности принимает вид

Пример 5. Найти угол между плоскостями, заданными уравнениями и

По формуле (3) получаем

т.е. данные плоскости перпендикулярны.

4.5. Расстояние от точки до плоскости

Т ребуется найти расстояние от плоскости до точки . М₀

Рассуждая аналогично, как и

для случая прямой на плоскости, d

(4)

Пример 6. Составить уравнение плоскости, параллельной плоскости и отстоящей от неё на расстояние

Уравнение искомой плоскости в силу условия параллельности имеет вид Возьмём любую точку, принадлежащую плоскости, например, точку . Тогда, используя формулу (4), получим