Как построить параболический цилиндр заданный уравнением (5 видео)

Содержание

Как построить параболический цилиндр заданный уравнением
6.2. Цилиндрические поверхности
Параболические цилиндры
Гиперболические цилиндры
Поверхности второго порядка. Цилиндрические поверхности.
🌟 Видео

Видео:Цилиндрические поверхностиСкачать

Как построить параболический цилиндр заданный уравнением

оси OY. Такие прямые целиком лежат на поверхности, «образуют» её, поэтому и называются образующими. Построенная поверхность называется параболическим цилиндром.

15. Построить поверхность, заданную уравнением .

Решение. Легко записать уравнение в каноническом виде: .

Так как переменной z нет, то это цилиндрическая поверхность. Строим в плоскости XOY гиперболу (её вершины находятся на оси OY). Через каждую точку гиперболы проводим прямую, параллельную оси OZ. Получаем гиперболический цилиндр.

16. Построить поверхность, заданную уравнением .

Решение. Так как уравнение не содержит произведений переменных, то для его преобразования к каноническому виду поворот осей не требуется, достаточно сделать параллельный перенос. Выделим полные квадраты:

Получили каноническое уравнение эллипсоида, центр которого находится в точке (1, —2, 0), полуоси a = 2, b = 3, c = 1.

17. Построить поверхность, заданную уравнением .

Решение. Заметим, что переменные x и y входят в уравнение только в составе суммы квадратов x 2 + ysup>2 . Значит, это поверхность вращения. Вокруг оси OZ вращается линия, уравнение которой получим, заменяя ременных, например, x:

Видео:Поверхности второго порядкаСкачать

6.2. Цилиндрические поверхности

Или цилиндры. Под цилиндром также понимают геометрическое тело.

И это не совсем то, что обычно подразумевает обыватель – класс цилиндрических поверхностей не ограничивается чёрным цилиндром на голове:

Задача 167

Построить поверхность, заданную уравнением

…что за дела?! Не опечатка ли здесь? Вроде как дано уравнение эллипса…

Нет, здесь не опечатка и все дела происходят именно в пространстве! Исследуем предложенную поверхность тем же методом, что использовали для плоскостей. Перепишем уравнение в виде , из которого следует, что «зет» принимает любые значения. Зафиксируем и построим в плоскости эллипс . Так как «зет» принимает все значения, то построенный эллипс непрерывно «тиражируется» вверх и вниз до бесконечности.

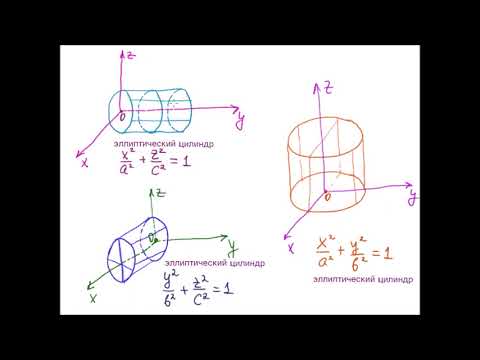
Данная поверхность называется эллиптическим цилиндром. Эллипс (на любой высоте) называется направляющей цилиндра, а параллельные прямые, проходящие через каждую точку эллипса называются образующими цилиндра (которые в прямом смысле слова его и образуют).

Ось является осью симметрии поверхности (но не её частью!).

Координаты любой точки, принадлежащей данной поверхности, обязательно удовлетворяют уравнению .

Пространственное неравенство задаёт «внутренность» бесконечной «трубы», включая саму цилиндрическую поверхность, и, соответственно, противоположное неравенство определяет множество точек вне цилиндра.

В практических задачах наиболее популярен частный случай, когда направляющей цилиндра является окружность:

Задача 168

Построить поверхность, заданную уравнением

Бесконечную «трубу» изобразить невозможно, поэтому художества ограничиваются, как правило, «обрезком».

Сначала удобно построить окружность радиуса в плоскости , а затем ещё пару окружностей сверху и снизу.

Полученные окружности (направляющие цилиндра) аккуратно соединяем 4 параллельными прямыми (образующими цилиндра):
Не забываем использовать пунктир для невидимых нам линий!

Координаты любой точки, принадлежащей данному цилиндру, удовлетворяют уравнению . Координаты любой точки, лежащей строго внутри «трубы», удовлетворяют неравенству , а неравенство задаёт множество точек внешней части. Для лучшего понимания рекомендую рассмотреть несколько конкретных точек пространства и убедиться в этом самостоятельно.

Часто эту поверхность некорректно называют круговым цилиндром. Круглым! Круговой цилиндр, строго говоря – есть тело, по той причине, что его направляющей является круг. И тело, кстати, определяется неравенством .

Задача 169

Построить поверхность и найти её проекцию на плоскость

Перепишем уравнение в виде , из которого следует, что «икс» принимает любые значения. Зафиксируем и в плоскости изобразим окружность – с центром в начале координат, единичного радиуса. Так как «икс» непрерывно принимает все значения, то построенная окружность порождает цилиндр с осью симметрии . Рисуем ещё одну окружность (направляющую цилиндра) и аккуратно соединяем их прямыми (образующими цилиндра). Местами получились накладки, но что делать, такой уж наклон:

На этот раз я ограничился кусочком цилиндра на промежутке и это не случайно. На практике зачастую и требуется изобразить лишь небольшой фрагмент поверхности.

Тут, к слову, получилось 6 образующих – две дополнительные прямые «закрывают» поверхность с левого верхнего и правого нижнего углов.

Теперь разбираемся с проекцией цилиндра на плоскость . Многие читатели понимают, что такое проекция, но, тем не менее, проведём очередную физкульт-пятиминутку:

Пожалуйста, встаньте и склоните голову над чертежом так, чтобы остриё оси смотрело перпендикулярно вам в лоб. То, чем с этого ракурса кажется цилиндр – и есть его проекция на плоскость . А кажется он бесконечной полосой, заключенным между прямыми , включая сами прямые. Данная проекция – это в точности область определения функций (верхний «жёлоб» цилиндра), (нижний «жёлоб»).

Давайте заодно проясним ситуацию и с проекциями на другие координатные плоскости. Пусть лучи солнца светят на цилиндр со стороны острия и вдоль оси . Тенью (проекцией) цилиндра на плоскость является аналогичная бесконечная полоса – часть плоскости , ограниченная прямыми ( – любое), включая сами прямые.

А вот проекция на плоскость несколько иная. Если смотреть на цилиндр из острия оси , то он спроецируется в окружность (не круг!) единичного радиуса , с которой мы начинали построение.

Задача 170

Построить поверхность и найти её проекции на координатные плоскости

Это задача для самостоятельного решения. Если условие не очень понятно, возведите обе части в квадрат и проанализируйте результат – выясните, какую именно часть цилиндра задаёт функция . Используйте методику построения, неоднократно применявшуюся выше. Краткое решение, чертёж и комментарии в конце книги.

Цилиндрические поверхности могут быть смещены относительно координатных осей, например:
– данное уравнение (по знакомым мотивам линий 2-го порядка) задаёт цилиндр единичного радиуса с линией симметрии, проходящей через точку параллельно оси .

Однако на практике подобные цилиндры попадаются довольно редко, и совсем уж невероятно встретить «косую» относительно координатных осей цилиндрическую поверхность.

Параболические цилиндры

Как следует из названия, направляющей такого цилиндра является парабола.

Задача 171

Построить поверхность и найти её проекции на координатные плоскости.

Не мог удержаться от этого примера =)

Решение: идём проторенной тропой. Перепишем уравнение в виде , из которого следует, что «зет» может принимать любые значения. Зафиксируем и построим обычную параболу на плоскости , предварительно отметив тривиальные опорные точки . Поскольку «зет» принимает все значения, то построенная парабола непрерывно «тиражируется» вверх и вниз до бесконечности. Откладываем такую же параболу, скажем, на высоте (в плоскости) и аккуратно соединяем их параллельными прямыми (образующими цилиндра):

Напоминаю полезный технический приём: если изначально нет уверенности в качестве чертежа, то линии сначала лучше прочертить тонко-тонко карандашом. Затем оцениваем качество эскиза, выясняем участки, где поверхность скрыта от наших глаз, и только потом придаём нажим грифелю.
Теперь вторая часть задания, отыскание проекций:

1) Проекцией цилиндра на плоскость является парабола .

2) Проекция цилиндра на плоскость представляет собой полуплоскость , включая ось

3) И, наконец, проекцией цилиндра на плоскость является вся плоскость .

Задача 172

Построить параболические цилиндры:

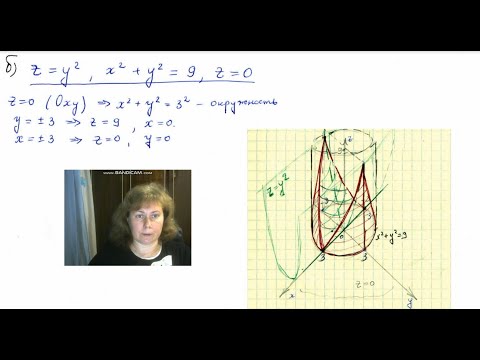
а) , ограничиться фрагментом поверхности в ближнем полупространстве;

б) на промежутке

В случае затруднений не спешим и рассуждаем по аналогии с предыдущими примерами, благо, технология досконально отработана. Не критично, если поверхности будут получаться немного корявыми – важно правильно отобразить принципиальную картину.

Я и сам особо не заморачиваюсь над красотой линий – если получился сносный чертёж «на троечку», обычно не переделываю. В образце решения, кстати, использован ещё один приём, позволяющий улучшить качество чертежа 😉

Гиперболические цилиндры

Направляющими таких цилиндров являются гиперболы.

Этот тип поверхностей, по моим наблюдениям, встречается значительно реже, и поэтому я ограничился единственным схематическим чертежом гиперболического цилиндра .