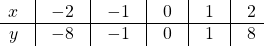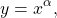Как построить кубическую параболу по уравнению

Видео:ЭЛЕМЕНТАРНО, ВАТСОН! Квадратичная Функция и ее график ПараболаСкачать

Кубическая функция

Кубическая функция — это функция вида y=ax³, где a — число ( a≠0).

График кубической функции называется кубической параболой.

Для начала рассмотрим свойства и график кубической функции y=x³ (при a=1).

Свойства функция y=x³:

1) Область определения — множество действительных чисел:

2) Область значений — все действительные числа:

3) Функция имеет один нуль:

4) Точка O (0;0) делит кубическую параболу на две равные части, каждая из которых называется ветвью кубической параболы. Ветви кубической параболы симметричны относительно точки O — начала координат.

Отсюда следует, что противоположным значениям x соответствуют противоположные значения y: (- x)³= — x³ .

5) Функция возрастает на всей числовой прямой.

6) Промежутки знакопостоянства: функция принимает положительные значения при x∈(0;∞) (или y>0 при x>0);

функция принимает отрицательные значения при x∈(-∞;0) (или y

Эти точки отмечаем на координатной плоскости и строим кубическую параболу:

График функции y=ax³ при a≠1 ( a≠0) получают из графика функции y=x³ при помощи геометрических преобразований.

Функция y=x³ — один из частных случаев степенной функции

где α — любое действительное число.

В курсе алгебры из частных случаев степенной функции мы уже встречались с квадратичной функцией y=x² и функцией обратной пропорциональности

Видео:Функция у=х² и у=х³ и их графики. Алгебра, 7 классСкачать

Построение графика кубической параболы.

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

График функции:Y= МЕТОДИЧЕСКОЕ И ПРАКТИЧЕСКОЕ пособие Учитель МБОУ СОШ №8 г. Каменск – Шахтинский Болдырева Н.Л.

Построим график зависимости Y= Вычислим координаты нескольких точек, удовлетворяющих условию, и заполним таблицу: x01-12-23-3 y01-18-827-27

Свойства кубической параболы: 1)Область определения x R 2)Множество значений y R 3)a>0,то функция y= возрастает при x R

4)При x=0.y=0-нули функции 5)График симметричен относительно начала координат. 6)График распределен в 1 и 3 координатных четвертях. 7)y>0 (функция принимает положительные значения) при x>0. Y

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 949 человек из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 681 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 314 человек из 70 регионов

Ищем педагогов в команду «Инфоурок»

Видео:3 ФУНКЦИИ ЗА ОДНО ВИДЕО — Кубическая функция, Y=|X| и Y=√(X) и их графикиСкачать

Дистанционные курсы для педагогов

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 567 241 материал в базе

Материал подходит для УМК

«Алгебра», Мордкович А.Г., Николаев Н.П.

§ 18. Четные и нечетные функции

Другие материалы

• 28.01.2018
• 2092
• 8

• 28.01.2018
• 318
• 0

• 28.01.2018
• 307
• 0

• 28.01.2018
• 447
• 3

• 28.01.2018
• 368
• 3

• 28.01.2018
• 1598
• 13

• 28.01.2018
• 3459
• 39

• 28.01.2018
• 800
• 16

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 28.01.2018 2370
• PPTX 1.7 мбайт
• 25 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Болдырева Наталья Леонидовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 5 лет и 4 месяца
• Подписчики: 1
• Всего просмотров: 18219
• Всего материалов: 21

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Функция y=x³ и ее график. 7 класс.Скачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Воронеже продлили удаленное обучение для учеников 5-11-х классов

Время чтения: 1 минута

Тринадцатилетняя школьница из Индии разработала приложение против буллинга

Время чтения: 1 минута

ЕГЭ в 2022 году будут сдавать почти 737 тыс. человек

Время чтения: 2 минуты

Профессия педагога на третьем месте по популярности среди абитуриентов

Время чтения: 1 минута

Онлайн-конференция о создании школьных служб примирения

Время чтения: 3 минуты

Рособрнадзор не планирует переносить досрочный период ЕГЭ

Время чтения: 0 минут

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Кубическая парабола и ее свойства - bezbotvyСкачать

Кубическая парабола

Вы будете перенаправлены на Автор24

Кубическая парабола – это парабола, задаваемая уравнением вида $y=ax^3$, где $a ≠ 0$. Также в литературе можно встретить и другие формулы для кубической параболы, все они эквивалентны.

Рисунок 1. График кубической параболы

Видео:Как строить параболу? | TutorOnlineСкачать

Свойства функции кубической параболы

1. График кубической параболы определён на всём пространстве действительных чисел.
2. Функция, задаваемая графиком кубической параболы, является нечётной, то есть: $f(-x) =(-x)^3= — x^3 = f(x)$.
3. Из этого следует, что обратная функция кубической параболы, заданная уравнением $y = -x^3$ будет располагаться II и IV четвертях графика, тогда как для $y = x^3$ график располагается в I и III четвертях.
4. График кубической параболы центрально-симметричен относительно начала координат или точки перегиба, если он сдвинут относительно начала координат. То есть форма кривой справа до точки перегиба полностью идентична форме кривой слева. График кубической параболы хотя бы 1 раз пересекает ось абсцисс.
5. График кубической параболы возрастает на всей области определения.

Видео:Всё о квадратичной функции. Парабола | Математика TutorOnlineСкачать

Анализ графика функции кубической параболы

1. Найдя производную $f'(x)$ кубической функции первого порядка и приравняв полученное выражение к нулю, вы получите критические точки для кубической параболы, называемые также локальными минимумами и максимумами.
2. Вторая производная $f»(x)$ параболы определяет точку перегиба функции.
3. Области значения и определения кубической параболы — все действительные числа.

Найдите точку перегиба для кубической параболы, заданной уравнением $y = 2x^3 + 6x^2 – x +2$.

1. Сначала найдём первую производную функции, она равна: $y’ = 6x^2 + 12x – 1$.
2. Теперь найдём вторую производную, $y» = 12x + 12$. Чтобы найти значение по оси абсцисс точки перегиба, приравняем вторую производную к нулю и решим уравнение: $12x + 12 = 0$, $x = -1$.
3. Найдём значение по оси ординат, для этого в исходную функцию подставим значение найденного $x$: $y = -2 + 6 + 1 +2 = 7$. Точка перегиба кубической параболы, заданной уравнением $y = 2x^3 + 6x^2 – x +2$ находится по координатам $(-1; 7)$.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 09 12 2021

🔥 Видео

Как легко составить уравнение параболы из графикаСкачать

Парабола. Квадратичная функцияСкачать

Кубическая параболаСкачать

Квадратичная функция и ее график. 8 класс.Скачать

Видеоурок "Парабола"Скачать

Построение параболыСкачать

Квадратическая и кубическая функции и их графики. Видеоурок по алгебре за 7 класс.Скачать

Как построить график функции без таблицыСкачать

Построить график | Кубическая парабола | Математика 9 класс | МегаШколаСкачать

Построение графика квадратичной функцииСкачать

§24 Каноническое уравнение параболыСкачать

Парабола | Квадратный трёхчлен #2 | Ботай со мной #021 | Борис ТрушинСкачать

КАК РЕШАТЬ КУБИЧЕСКИЕ УРАВНЕНИЯ | Разбираем на конкретном примереСкачать