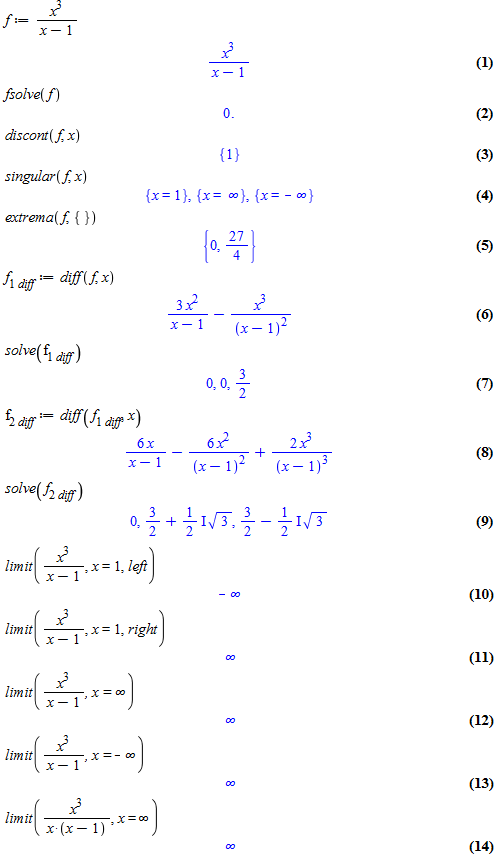Как построить график в maple по уравнению (8 видео)

Содержание

Как построить график в maple по уравнению
Задание 1.1.
Задание 1.2.
Типовые средства построения графиков
Maple: Исследование функций и построение графиков
🔍 Видео

Видео:Графики, функции, решение системы линейных уравнений в MapleСкачать

Как построить график в maple по уравнению

Команда plot и ее параметры.

Для построения графиков функции f(x) одной переменной (в интервале по оси Ох и в интервале по оси Оу ) используется команда plot(f(x), x=a..b, y=c..d, parameters), где parameters – параметры управления изображением. Если их не указывать, то будут использованы установки по умолчанию. Настройка изображения также может осуществляться с панели инструментов.

Основные параметры команды plot :

1) title=”text”, где text- заголовок рисунка (текст можно оставлять без кавычек, если он содержит только латинские буквы без пробелов).

2) coords=polar – установка полярных координат (по умолчанию установлены декартовы).

3) axes – установка типа координатных осей: axes=NORMAL – обычные оси; axes=BOXED – график в рамке со шкалой; axes=FRAME – оси с центром в левом нижнем углу рисунка; axes=NONE – без осей.

4) scaling – установка масштаба рисунка: scaling=CONSTRAINED – одинаковый масштаб по осям; scaling=UNCONSTRAINED – график масштабируется по размерам окна.

5) style=LINE(POINT) – вывод линиями (или точками).

6) numpoints=n – число вычисляемых точек графика (по умолчанию n=49 ).

7) сolor – установка цвета линии: английское название цвета, например, yellow – желтый и т.д.

8) xtickmarks=nx и ytickmarks=ny – число меток по оси Оx и оси Оy , соответственно.

9) thickness=n, где n=1,2,3… — толщина линии (по умолчанию n=1 ).

10) linestyle=n – тип линии: непрерывная, пунктирная и т.д. ( n=1 – непрерывная, установлено по умолчанию).

11) symbol=s – тип символа, которым помечают точки: BOX, CROSS, CIRCLE, POINT, DIAMOND .

12) font=[f,style,size] – установка типа шрифта для вывода текста: f задает название шрифтов: TIMES, COURIER, HELVETICA, SYMBOL; style задает стиль шрифта: BOLD, ITALIC, UNDERLINE; size – размер шрифта в pt.

13) labels=[tx,ty] – надписи по осям координат: tx – по оси Оx и ty – по оси Оy .

14) discont=true – указание для построения бесконечных разрывов.

С помощью команды plot можно строить помимо графиков функций y=f(x), заданной явно, также графики функций, заданных параметрически y=y(t), x=x(t) , если записать команду plot([y=y(t), x=x(t), t=a..b], parameters) .

Видео:Графика в системе MapleСкачать

Задание 1.1.

Построить график жирной линией в интервале от -4 p до 4 p . Наберите:

> plot(sin(x)/x, x=-4*Pi..4*Pi, labels=[x,y],

Построить график разрывной функции .

Замечание : на рисунке автоматически появляются вертикальные асимптоты.

Построить график параметрической кривой , , в рамке. Наберите:

> plot([sin(2*t),cos(3*t),t=0..2*Pi], axes=BOXED, color=blue);

Построить в полярных координатах график кардиоиды с названием. Наберите:

> plot(1+cos(x), x=0..2*Pi, title=»Cardioida», coords=polar, color=coral, thickness=2);

Построить два графика на одном рисунке: график функции

Как построить график в maple по уравнению

и касательную к нему

Наберите:

Построение графика функции, заданной неявно.

Функция задана неявно, если она задана уравнением . Для построения графика неявной функции используется команда implicitplot из графического пакета plots: implicitplot(F(x,y)=0, x=x1..x2, y=y1..y2).

Вывод текстовых комментариев на рисунок.

В пакете plots имеется команда textplot для вывода текстовых комментариев на рисунок: textplot([xo,yo,’text’], options), где xo, yo – координаты точки, с которой начинается вывод текста ’text’ .

Вывод нескольких графических объектов на один рисунок.

Часто бывает необходимо совместить на одном рисунке несколько графических объектов, полученных при помощи различных команд, например, добавить графику, нарисованному командой plot , текстовые надписи, полученные командой textplot . Для этого результат действия команды присваивается некоторой переменной:

При этом на экран вывод не производится. Для вывода графических изображений необходимо выполнить команду из пакета plots:

> with(plots): display([p,t], options) .

Построение двумерной области, заданной неравенствами.

Если необходимо построить двумерную область, заданную системой неравенств , то для этого можно использовать команду inequal из пакета plots . В команде inequals(c1,…,fn(x,y)>cn>, x=x1…x2, y=y1..y2, options) в фигурных скобках указывается система неравенств, определяющих область, затем размеры координатных осей и параметры. Параметры регулируют цвета открытых и закрытых границ, цвета внешней и внутренней областей, а также толщину линий границ:

optionsfeasible=(color=red) – установка цвета внутренней области;

optionsexcluded=(color=yellow) – установка цвета внешней области;

optionsopen(color=blue, thickness=2) – установка цвета и толщины линии открытой границы;

optionsclosed(color=green,thickness=3) – установка цвета и толщины линии закрытой границы.

Видео:Анимация в MapleСкачать

Задание 1.2.

Построить график неявной функции (гиперболы):

2. Построить на одном рисунке графики астроиды , () вписанной в эллипс . Выведите название линий Astroida и Ellips жирным шрифтом вместе с его уравнением курсивом. Для этого наберите следующие строки:

> el:=implicitplot(eq, x=-4..4, y=-2..2, scaling=CONSTRAINED,

color=blue, scaling=CONSTRAINED, thickness=2):

ITALIC, 10], align=RIGHT):

3. Построить область, ограниченную линиями: , , .

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Видео:вспоминаем maple 01 график кусочно-непрерывной функции через `if`Скачать

Типовые средства построения графиков

Основные возможности двумерной графики

Maple 7 реализует все мыслимые (и даже «немыслимые») варианты математических графиков. Строятся как графики простых функций в декартовой и полярной системах координат, так и графики, показывающие реалистические образы сложных, пересекающихся в пространстве фигур с их функциональной окраской. Возможны наглядные графические иллюстрации решений самых разнообразных уравнений, включая системы дифференциальных уравнений.

В само ядро Maple 7 встроено ограниченное число функций построения графиков. Это прежде всего функция для построения двумерных графиков plot и функция для построения трехмерных графиков plotSd . Они позволяют строить графики наиболее распространенных типов. Для построения специальных графиков (например, векторных полей градиентов, решения дифференциальных уравнений, построения фазовых портретов и т. д.) в пакеты системы Maple 7 включено большое число различных графических функций. Для их вызова необходимы соответствующие указания.

Вообще говоря, средства для построения графиков в большинстве языков программирования принято считать графическими процедурами, или операторами. Однако мы сохраним за ними наименование функций, в силу двух принципиально важных свойств:

О графические средства Maple V возвращают некоторые графические объекты, которые размещаются в окне документа — в строке вывода или в отдельном графическом объекте;

О эти объекты можно использовать в качестве значений переменных, то есть переменным можно присваивать значения графических объектов и выполнять над ними соответствующие операции (например, с помощью функции show выводить на экран несколько графиков).

Графические функции заданы таким образом, что обеспечивают построение типовых графиков без какой-либо особой подготовки. Для этого нужно лишь указать функцию, график которой строится, и пределы изменения независимых переменных. Однако с помощью дополнительных необязательных параметров можно существенно изменить вид графиков — например, настроить стиль и цвет линий, вывести титульную надпись, изменить вид координатных осей и т. д.

Основная функция построения двумерных графиков plot

В математике широко используются зависимости вида y(x) или у(х). Их графики строятся на плоскости в виде ряда точек y 1 (x 1 ) , обычно соединяемых отрезками прямых. Таким образом, используется кусочно-линейная интерполяция двумерных графиков. Если число точек графика достаточно велико (десятки или сотни), то приближенность построения не очень заметна.

Для построения двумерных графиков служит функция plot . Она задается в виде:

где f — визуализируемая функция (или функции), h — переменная с указанием области ее изменения, v — необязательная переменная с указанием области изменения, о — параметр или набор параметров, задающих стиль построения графика (толщину и цвет кривых, тип кривых, метки на них и т. д.).

Самыми простыми формами задания этой функции являются следующие:

plot(f ,xrnin,xmax) — построение графика функции f, заданной только своим именем;
pl ot(f(x),x=xmin,xmax) — построение графика функции f(x),

Диапазон изменения независимой переменной х задается как xmin. xmax , где xmin и xmax — минимальное и максимальное значение х, .. (две точки) — составной символ, указывающий на изменение независимой переменной. Разумеется, имя х здесь дано условно — независимая переменная может иметь любое допустимое имя.

Помимо построения самой кривой у(х) или f(x) необходимо задать ряд других свойств графиков, например вывод координатных осей, тип и цвет линий графика и др. Это достигается применением параметров графика — специальных указаний для Maple. Графики обычно (хотя и не всегда) строятся сразу в достаточно приемлемом виде. Это достигается тем, что многие параметры задаются по умолчанию и пользователь, по крайней мере начинающий, может о них ничего не знать. Однако язык общения и программирования Maple 7 позволяет задавать управляющие параметры и в явном виде.

Для двумерного графика возможны следующие параметры:

adaptive — включение адаптивного алгоритма построения графиков (детали см. ниже);
axes — вывод различных типов координат ( axes=NORMAL — обычные оси, выводятся по умолчанию, axes=BOXES — график заключается в рамку с осями-шкалами, axes=FRAME — оси в виде перекрещенных линий, axes=NONE — оси не выводятся);
axes font — задание шрифтов для подписи делений на координатных осях (см. также параметр font );
color — задает цвет кривых (см. далее);
coords — задание типа координатной системы (см. далее);
discont — задает построение непрерывного графика (значения true или false );
filled — при filled=true задает окраску цветом, заданным параметром color , для области, ограниченной построенной линией и горизонтальной координатной осью х;
font — задание шрифта в виде [семейство, стиль, размер];
labels — задание надписей по координатным осям в виде [X, Y], где X и Y — надписи по осям х и у графика;
label directions — задает направление надписей по осям [X, Y], где X и Y может иметь строковые значения HORISONTAL (горизонтально) и VERTICAL (вертикально);
label font — задает тип шрифта подписей (см. font);
legend — задает вывод легенды (обозначения кривых);
linestyle — задание стиля линий (1 — сплошная, 2 — точками, 3 — пунктиром и 4 — штрихпунктиром);
numpoints — задает минимальное количество точек на графике (по умолчанию numpoints =49);
resolutions — задает горизонтальное разрешение устройства вывода (по умолчанию resolutions =200, параметр используется при отключенном адаптивном методе построения графиков);
sample — задает список параметров для предварительного представления кривых;
scaling — задает масштаб графика: CONSTRAINED (сжатый) или UNCONSTRAINED (несжатый — по умолчанию);
size .— задает размер шрифта в пунктах;
style — задает стиль построения графика ( POINT — точечный, LINE — линиями);
symbol — задает вид символа для точек графика (возможны значения BOX — прямоугольник, CROSS — крест, CIRCLE — окружность, POINT — точка, DIAMOND — ромб);
symbol size — установка размеров символов для точек графика (в пунктах, по умолчанию 10);
title — задает построение заголовка графика ( title=»string», где string — строка);
title f ont — определяет шрифт для заголовка (см. font);
thickness — определяет толщину линий графиков (О, 1, 2, 3, значение по умолчанию — 0);
view=[A, В] — определяет максимальные и минимальные координаты, в пределах которых график будет отображаться на экране, А = [xmin. .xmax], B=[ymin. .ymax] (по умолчанию отображается вся кривая);
xtickmarks — задает минимальное число отметок по оси x,
ytickmarks — задает минимальное число отметок по оси у.

В основном задание параметров особых трудностей не вызывает, за исключением задания титульной надписи с выбором шрифтов по умолчанию — в этом случае не всегда поддерживается вывод символов кириллицы (русского языка). Подбором подходящего шрифта эту проблему удается решить. Модификация графиков с помощью управляющих параметров подробно рассматривается ниже.

Специальный параметр adaptive задает работу специального адаптивного алгоритма для построения графиков наилучшего вида. При этом Maple автоматически учитывает кривизну изменения графика и увеличивает число отрезков прямых в тех частях графиков, где их ход заметно отличается от интерполирующей прямой. При задании adaptive=false адаптивный алгоритм построения графиков отключается, а при adaptive=true включается (значение по умолчанию).

Задание координатных систем двумерных графиков

В версии Maple 7 параметр coords задает 15 типов координатных систем для двумерных графиков. По умолчанию используется прямоугольная (декартова) система координат ( coords=cartesian). При использовании других координатных систем координаты точек для них(и, v) преобразуются в координаты (х, у) как (n, v) —> (х, у) . Ниже приведены наименования систем координат (значений параметра coords ) и соответствующие формулы преобразования.

x = sinh(v)/(cosh(v)-cos(u)) у — sin(u)/(cosh(v)-cos(u))

Видео:Построение 3D моделей в Maple 15Скачать

Maple: Исследование функций и построение графиков

Важным разделом математики является исследование аналитических функций. Оно обычно заключается в определении координат особых точек функции и ее значений в этих точках, а также в выяснении особенностей функции, таких как наличие точек разрыва, асимптот, точек перегибов, разрывов и т. д.

Maple 16, как и более ранние версии этого пакета, позволяют студенту полностью исследовать функции и строить их графики.

С помощью функции fsolve легко находятся значения независимой переменной x функций вида f(x), при которых f(x)=0 (корни этого уравнения). При этом данная функция позволяет (в отличие от функции solve) изолировать корни функции f(x) указанием примерного интервала их существования. Ряд функций служит для вычисления экстремумов, максимумов и минимумов функций, а также для определения их непрерывности.

Для исследования функций на непрерывность Maple 16 имеет функцию iscont, записываемую в ряде форм: iscont(expr, x=a..b), iscont(expr, x=a..b, ‘closed’) и iscont( expr, x=a.. b, ‘open’).

Функции, не имеющие непрерывности, доставляют много хлопот. В Maple 16 функция discont(f, х) позволяет определить точки, в которых нарушается непрерывность функции f(x). Она вычисляет все точки в пределах изменениях от $$-infty$$ до $$infty.$$ Результаты вычислений могут содержать особые экстра переменные с именами вида _Zn- и _NNn-. В частности, они позволяют оценить периодические нарушения непрерывности функций.

Многие операции, такие как интегрирование и дифференцирование, чувствительны к особенностям функций, в частности к их разрывам и особым точкам. Функция singular(ехрr, vars) позволяет найти особые (сингулярные) точки выражения ехрг, в которых она испытывает разрывы. Дополнительно в числе параметров может указываться необязательный список переменных.

Функция extrema позволяет найти экстремумы выражения ехрr (как максимумы, так и минимумы) при ограничениях constraints и переменных vars, по которым ищется экстремум: extrema(expr, constraints), extrema(expr, constraints, vars) и extrema(expr, constraints, vars, ‘s’).

Ограничения constraints и переменные vars могут задаваться одиночными объектами или списками ряда ограничений и переменных. Найденные координаты точки экстремума присваиваются переменной ‘s’. При отсутствии ограничений в виде равенств или неравенств вместо них записывается пустой список .

Функция extrema возвращает как значения экстремумов, так и значения аргументов, при которых экстремумы наблюдаются.

Часто нужно найти минимум или максимум заданной функции. Для поиска минимумов и максимумов выражений (функций) ехрr служат функции стандартной библиотеки: minimize(expr, opt1, opt2, …, optn) и maximize(expr, opt1, opt2, …, optn).

Эти функции могут разыскивать максимумы и минимумы для функций как одной, так и нескольких переменных. С помощью опций optl, opt2, … , optn можно указывать дополнительные данные для поиска.

Для вычисления пределов функции f в точке x=a используются следующие функции: limit(f, x=a, dir) и Limit(f, x=a, dir).

Здесь f — алгебраическое выражение, х — имя переменной, dir — параметр, указывающий на направление поиска предела (left — слева, right — справа, real — в области вещественных значений, complex — в области комплексных значений). Значением а может быть бесконечность (как положительная, так и отрицательная).

Для нахождения производной применяют дифференциальный оператор, который можно записывать в следующих формах: D(f) или D[i](f), где параметр f — выражение или имя функции, i — положительное целое число, выражение или последовательность. Этот оператор позволяет сократить запись, т.е. D(f)=unapply(diff(f(x), x), x) а в форме D(f)(x) = diff(f(x), x). Для нахождения n–й производной используют ([email protected]@n)(f).

Для построения двумерных графиков служит функция plot. Она задается в виде: plot(f, h, v) и plot(f, h, v,…) ,где f — визуализируемая функция (или функции), h — переменная с указанием области ее изменения по горизонтали, v — необязательная переменная с указанием области изменения функции по вертикали, далее может следовать параметр или набор параметров, задающих стиль построения графика (толщину и цвет кривых, тип кривых, метки на них и т.д.). Обычно записывают plot(f(x), x=a..b). Диапазон изменения независимой переменной x задается как a..b, где a и b — минимальное и максимальное значение x, .. (две точки) — составной символ, указывающий на изменение независимой переменной. Разумеется, имя х здесь дано условно — независимая переменная может иметь любое допустимое имя.

Помимо построения самой кривой f(x) необходимо задать ряд других свойств графиков, например вывод координатных осей, тип и цвет линий графика и др. Это достигается применением параметров графика — специальных указаний для Maple. Графики обычно (хотя и не всегда) строятся сразу в достаточно приемлемом виде. Это достигается тем, что многие параметры задаются по умолчанию и пользователь, по крайней мере начинающий, может о них ничего не знать. Однако язык Maple 16 позволяет задавать управляющие параметры и в явном виде.

Пример

Исследовать функцию и построить график

Исследуем функцию средствами Maple 16: