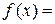Как построить график уравнения в матлабе (8 видео)

Построение графиков функций

Здравствуйте! В этой статье мы разберем построение графиков на MATLAB для различных математических функций, а также научимся выводить несколько графиков одновременно.

Содержание

Где прописывать код
Графики MATLAB
2. Графика matlab
Построение графиков.
📽️ Видео

Видео:MATLAB 07 Интерактивное построение графиковСкачать

Где прописывать код

Но для начала научимся создавать скрипты в Matlab. Так вам будет удобнее работать с Matlab, писать коды и вообще приятнее, когда видишь всю программу сразу, а не построчно. Делается это просто: нажать New —> Script —> ScriptCtrl+N.

Откроется вот такое окно:

После того, как вы напишите сюда свой код, нужно его запустить. Это делается с помощью вот этой кнопки.

Видео:Графики в MATLABСкачать

Графики MATLAB

Построение графиков функций в MATLAB можно реализовать разными способами, например, через plot или polar, с полным списком можете ознакомиться здесь.
Но сейчас речь пойдёт о функции ezplot.
Разберём такой пример:

Построить графики функций y=e^((-x^2)/2) и у =x^4-x^2 для -1.5 ≤ x ≤1.5 на одной и той же координатной сетке.

Открываем скрипт и пишем нехитрый код:

Вывод:

На этом примере мы видим, как работает функция ezplot(), где в качестве аргументов указывается функция без ‘y=’ и интервал значений в квадратных скобках. Чтобы построить два графика в одном окне используем hold on. А axis tight — устанавливает границы осей в диапазоне данных значений.
Разберём ещё один:

Построить график функции y=x^3-x для интервала -4≤x≤4.
Как вы догадались, скрипт будет такой:

Его скорее всего проще записать в компилятор напрямую.
Давайте ещё один:

Построить график функции у=sin(1/x^2) для интервала -2 ≤ x ≤2.

И последний:

Построить график функции y=tan(x/2) для интервала — π ≤ x ≤ π и -10 ≤ y ≤10.

В данном случае мы указали границы оси с помощью axis от -π до π.

Если остались вопросы по поводу построения графиков функций в MATLAB, то обязательно пишите в комментариях, ответим.

Видео:MatLab. Урок 3. Функции и построение графиков.Скачать

2. Графика matlab

График даёт самую полную общую информацию о функции, поэтому в системах компьютерной математики большое внимание уделяется средствам построения графиков функций.

В MATLAB имеется три функции построения двумерных графиков: plot() , fplot( ) и ezplot( ).

Функция plot() строит графики кривых с массивами значений абсцисс и ординат и имеет следующий формат:

Строка s используется для задания параметров графика: типа, толщины и цвета рисуемой линии, а также формы и размера меток на графике. Строка s может отсутствовать, тогда MATLAB устанавливает параметры, действующие по умолчанию: все кривые выводятся сплошными линиями, окрашенными циклически в шесть различных цветов.

Переменная s представляет собой строку символов, и эту строку можно подготовить в отдельной команде или записать непосредственно в команде построения графика, например

Таблица кодировки типов линий при выводе графика функции

Таблица кодировки цвета линии графика функции

Таблица кодировки меток на графике

^ v > > x=0:0.01:3; y=exp(x).*sin(9*x); plot(x, y,’r-‘)

Для построения графиков используется специальный графический редактор, который строит на экране графическое окно и в нём рисует график. Вызывается графический редактор автоматически при выполнении графических функций. По умолчанию производится разметка осей координат и иногда выводится заголовок сверху графика. Графический редактор имеет свои средства модификации графика и нанесения на график различных надписей и символов. Например, заголовок создаёт функция titke(‘text’), причём в качестве параметра text можно использовать и формулу.

Пример. Построить график функции с заголовком.

Текст можно вывести в заданное координатами место графика функцией .

>> text(0.5, 15, ‘grafik y=exp(x)sin(9x)’)

Координаты вывода текста можно указать на графике мышью, если использовать функцию . Тогда после вывода графика и выполнения команды

нужно указать мышью место на графике и щёлкнуть.

На одном чертеже можно построить графики нескольких функций, для этого нужно попарно перечислить векторы, задающие абсциссы и ординаты. Для идентификации графиков можно использовать команду legend(), позволяющую связать с каждой кривой некоторую текстовую информацию.

Пример. Построить на одном чертеже графики функций и

>> x=0:0.02:pi; y=exp(x);z=sin(9*x);plot(x, y,x, z), legend(‘exp(x)’, ‘sin(9x)’)

Имеется другой способ размещения на одном чертеже графиков нескольких функций: сформировать матрицу, столбцы которой должны содержать нужные ординаты. Ординаты обычно удобно задавать строками, тогда для построения графиков строки необходимо транспонировать.

Пример. Построить на одном чертеже графики функций .

а) Построить график функции на промежутке с шагом . График рисовать сплошной линией красного цвета.

6) Построить график функции на промежутке с шагом . График рисовать пунктирной линией чёрного цвета с маркерами в виде пятиконечной звезды размера 5.

в) Построить на одном чертеже графики функций .

г) Построить на одном чертеже графики функций . Использовать функцию для идентификации графиков.

д) Построить на одном чертеже графики функций . Использовать функцию .

Функция ezplot() применяется для рисования графиков неявно заданных функции двух переменных и параметрически заданных функций. Эта функция рисует также графики функций одной переменной, причём, в огтличие от функции plot(), шаг и нужные массивы значений абсцисс и ординат соэдаются автоматически. Функция ezplot() автоматически выводит над графиками наименование функций.

Пример. Построить на промежутке график функции . Нанести на график сетку.

Пример. Построить на промежутке график неявной функции, заданной уравнением .

Функция ezplot() особенно удобна для определения начального приближения решения системы двух уравнений графическом методом Нужно построить на одном чертеже графики двух неявных функций и . Эту задачу решают две последовательно выполненные команды

В первой команде используется функция hold, чтобы сохранить рисунок для последующего наложения на него второго рисунка.

Пример. Найти начальное приближение решения системы

Рисунок показывает, что система имеет четыре решения, приближённые значения которых есть , , , .

Задача 8 . Найти графическим методом начальные приближения решений системы ( N−номер варианта):

2.3. Построение нескольких рисунков в одном графическом окне

В одном графическом окне можно разместить несколько рисунков, используя функцию subplot(N,M,K). Эта функция создаёт массив графиков, состоящий из N рисунков по вертикали и M рисунков по горизонтали. В результате выполнения функции subplot(N,M,K) активным становится рисунок с номером K. Нумерация ведётся слева направо и сверху вниз. Крайний слева рисунок из верхнего ряда считается первым, а крайний справа из нижнего ряда имеет номер N*M.

Пример. В одном графическом окне построить графики четырёх функций: на промежутке , на промежутке , на промежутке и на промежутке .

Решение. Выполним следующие команды, не закрывая графического окна:

>> subplot(2,2,1), ezplot(‘x^2’,[-5,5]), xlabel(»),grid

>> subplot(2,2,2), ezplot(‘exp(x)’,[-2,2]), xlabel(»),grid

>> subplot(2,2,3), ezplot(‘log(x)’,[0,5]), xlabel(»),grid

>> subplot(2,2,4), ezplot(‘sqrt(x)’,[0,10]), xlabel(»),grid

В командах вывода графиков использована функция xlabel(‘’) с аргументом в виде пустой строки, которая отменяет вывод обозначения горизонтальной оси. Если этого не сделать, то символ обозначения оси наложится на наименование функций нижних графиков.

Функция fplot(‘f(x)’, [xmin, xmax]), аналогично функции plot(), строит график функции f(x), однако при использовании функции fplot() не требуется задавать массив значений аргумента и вычислять массив

значений функции, всё это делается автоматически. График строится на промежутке изменения аргумента x от xmin до xmax.

Пример. Построить график функции на промежутке .

Решение. Используем функцию fplot():

2.5. Трёхмерная графика

Чтобы построить поверхность , нужно иметь массив значений функции , вычисленный на некоторой сетке. Для формирования двумерной прямоугольной сетки используется функция meshgrid(x,y), где x,y−одномерные массивы точек, задающие абсциссы и ординаты двумерной функции.

Пример. Построить поверхность .

>> x=0:0.2:8; y=0:0.2:4; [X, Y]=meshgrid(x, y); Z=2*cos(X+Y)+Y.*cos(X-Y); mesh(X, Y,Z)

Функция mesh() строит расцвеченную сетчатую поверхность, используя различную окраску вершин и рёбер.

Кроме функции mesh(), для изображения поверхности имеются и другие функции:

meshc()−строится сетчатая поверхность с линиями уровня;

meshz()−строится сетчатая поверхность и отсчётная плоскость;

surf()−строится расцвеченная поверхность;

surfc()−строится расцвеченная поверхность с линиями уровня;

surfl()−строится расцвеченная поверхность с подсветкой;

waterfall−строится поверхность без прорисовки ребер.

Пример. Построим поверхность этими функциями.

После построения рисунков для каждого рисунка можно выполнить масштабирование функцией axis([-Inf Inf —Inf Inf —Inf Inf]). Например, второй рисунок промасштабирует команда

При масштабировании определяются действительные интервалы изменения величин по всем координатам и рисунки становятся выразительнее.

1) Построить поверхность функцией на сетке x=0:0.2:8;y=0:0.2:4. Использовать режим вращения изображения для изменения ракурса. Режим вращения задаётся нажатием соответствующего значка на панели инструментов графического окна.

2) Эту же поверхность построить на более мелкой сетке x=0:0.05:8; y=0:0.05:4.

3) Эту же поверхность построить на сетке x=0:0.02:8;y=0:0.01:6

4) Построить поверхность функцией на сетке x=0:0.2:8; y=0:0.1:6

5) Выбрать сетку и построить поверхность функцией

6) Построить в одном графическом окне три поверхности : одну на сетке x=0:0.1:8;y=0:0.1:4, вторую на сетке x=0:0.05:8;y=0:0.05 и третью на сетке x=0:0.01:8;y=0:0.01:4.

7) Выбрать сетку и построить в одном графическом окне четыре поверхности при следующих значениях параметров и :

8) Построить в одном окне поверхность функциями и на сетке x=-pi:0.1:pi; y=-pi:0.1:pi. Выполнить масштабирование рисунков.

9) Построить поверхность функцией на сетке x=-pi:0.1:pi; y=-pi:0.1:pi. Установить единый масштаб по осям абсцисс и ординат, выбрать и установить ракурс, удалить сетку.

Видео:Как оформить график в MatLab.Скачать

Построение графиков.

Основная команда для построения графиков функций одной переменной в MATLAB – команда plot. При этом графики строятся в отдельных масштабируемых и перемещаемых окнах (Figure).

Возьмем вначале простейший пример – построим график синусоиды. Следует помнить, что MATLAB строит графики функций по ряду точек, соединяя их отрезками прямых, т. е. осуществляя линейную интерполяцию функции в интервале между соседними точками. Зададим интервал изменения аргумента х от 0 до 10 с шагом 0.1.

Текст соответствующего M-файла:

x=0:0.1:10; y=sin(x); plot(x,y)

Графическое окно с результатом представлено на рис. 1.

Рис. 1. Графическое окно, в котором построен график синусоиды.

Дополнительные возможности для оформления графиков:

· hold on (hold off) – объединение (отключение) нескольких графиков на одних координатных осях;

· grid on (grid off) – нанесение (отключение) линий сетки на график;

· title(‘заголовок’) – вывод заголовка функции;

· xlabel(‘подпись под осью x’),ylabel(‘подпись под осью y’) – соответственно подписи осей х и у;

· text(m,n,’надпись’)– надпись в заданном месте рисунка, m и n – координаты точки на графике, начиная с которой выводится запись (координаты точки задаются в тех же единицах измерения, что и координаты осей графика);

· legend(‘легенда 1’, ‘легенда 2’, … , ‘легенда n’, k)– легенды для каждого из n-графиков k – местоположение легенды.

· Функцияsubplot(m,n,p) – это разделение графического окна MATLAB на несколько подокон с различными графиками, где m и n – число частей по вертикали и по горизонтали, на которые делится графическое окно, p – номер подокна в котором нужно отобразить график.

Полная форма команды построения графиков функций одной переменной:

где x1, x2, … , xn – массивы абсцисс графиков; y1, y2, …, yn – массивы ординат; s1, s2, … , sn – строка, состоящая из трех символов, которые определяют цвет линии, тип маркера и тип линии графиков.

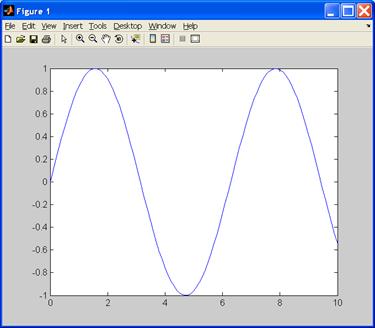
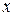
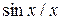
Кроме того, для построения графиков функций одной переменной можно использовать графическую функцию fplot. Она позволяет строить график функции, заданной в символьном виде (например, арифметическое выражение, определяющее функцию, заключено в апострофы), в интервале изменения аргумента от xmin до xmax без фиксированного шага изменения х. Рассмотрим ее применение для построения графика функции на интервале от -10 до 10. Эта функция имеет устранимую неопределенность в точке 0. Построение ее графика с помощью plot в этой точке не представляется возможным. Соответствующее графическое окно с графиком представлено на рис. 2. Заметим, что в точке результат правильный, т.е. .

Текст соответствующего M-файла:

fplot(‘sin(x)/x’,[-10,10]);grid on

Рис. 2. Графическое окно, в котором построен график sin(x)/x.

Команда grid on (сетка) позволяет включить отображение сетки, которая строится пунктирными линиями.

Таблица 1.6. Параметры для управления цветом и видом графиков.

Параметр	Обозначение
Тип линии
сплошная	—
пунктирная	:
штриховая	—
штрихпунктирная	-.
Цвет линии
красный	r
желтый	y
зеленый	g
синий	b
голубой	c
розовый	m
черный	k
белый	w
Тип маркера
точка	.
кружок	о
крестик	x
плюс	+
звездочка	*
квадрат	s
ромб	d
треугольник вершиной вниз	v
треугольник вершиной вверх	^