Программа MathCAD обеспечивает стабильное поддержание своих функций уже долгие годы. В этой вычислительной среде работают экономисты, ученые, студенты и другие специалисты, владеющие прикладной и аналитической математикой. Так как математический язык понятен не всем, и не каждый способен за быстрое время его изучить, программа становится сложной для восприятия начинающих пользователей. Нагруженный интерфейс и большое количество нюансов отталкивают людей от использования этого продукта, но на самом деле разобраться в любой рабочей среде возможно — достаточно иметь желание. В этой статье разберем такую важную тему, как построение графиков функций в «Маткаде». Это несложная процедура, которая очень часто помогает при расчетах.
Видео:MathCAD Построение графика быстрым способомСкачать
Типы графиков
Помимо того что в MathCAD определены быстрые графики, которые вызываются с помощью горячих клавиш, существуют и другие графические приложения. Например, пользователь может в шапке программы найти раздел «Вставка», а в ней — подраздел «График», в котором можно просмотреть все доступные графики в «Маткаде»:
- График X-Y — показывает зависимость одной величины от другой. Самый распространенный тип, который позволяет быстро оценить и исследовать зависимости.
- Полярный график — использует полярные координаты. Суть графика — показать зависимость одной переменной от другой только в полярной координатной плоскости.
- График поверхности — создает поверхность в пространстве.
- Векторное поле, 3-D график разброса, столбчатая 3-D диаграмма используются для других специальных целей.
Видео:Основы работы в Mathcad ГрафикиСкачать

Построение графика функции
Невозможно научиться работать с вычислительной средой без примеров, поэтому будем разбираться в MatchCAD на шаблоне.
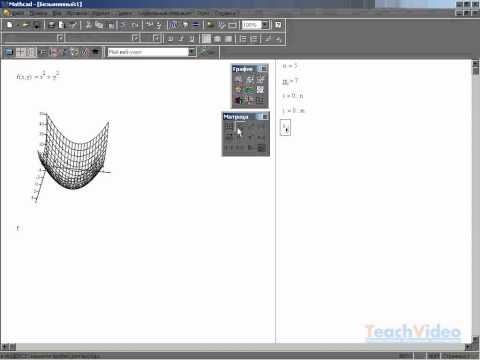
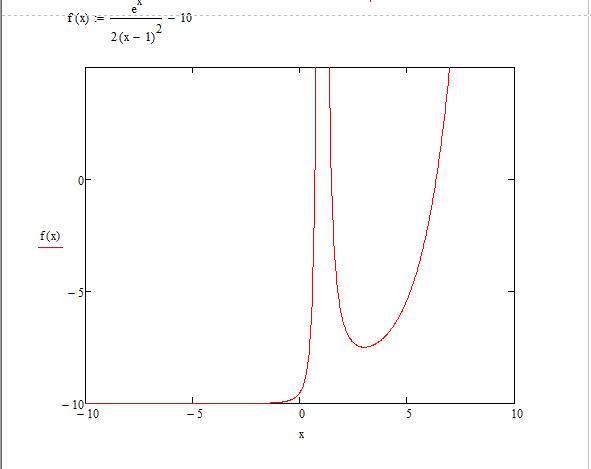
Допустим, задана функция f(x) = (e^x/(2x-1)^2)-10 в интервале [-10;10], которую необходимо построить и провести исследование. Прежде чем приступить к построению графика функции, необходимо данную функцию перевести в математический вид в самой программе.
- После того как функция была задана, следует вызвать окно быстрого графика клавишей Shift + 2. Появляется окошечко, в котором расположены 3 черных квадратика по вертикали и горизонтали.
- По вертикали: самый верхний и нижний отвечают за интервалы значений, которые можно регулировать, средний задает функцию, по которой пользователь может построить график в «Маткаде». Крайние черные квадратики оставляем без изменения (значения автоматически присвоятся после построения), а в средний пишем нашу функцию.
- По горизонтали: крайние отвечают за интервалы аргумента, а в средний нужно вписать «х».
- После проделанных шагов нарисуется график функции.
Видео:MathCAD Решение системы уравненийСкачать

Построение графика по точкам в «Маткаде»
Иногда тяжело задать функцию или посчитать ее значение, поэтому для ее построения используют метод диапазонов. В техническом задании может быть дан только диапазон значений, по которому необходимо воспроизвести изображение.
- Зададим диапазон значений для аргумента, в рассматриваемом случае x:=-10,-8.5.. 10 (символ «..» ставится при нажатии на клавишу «;»).
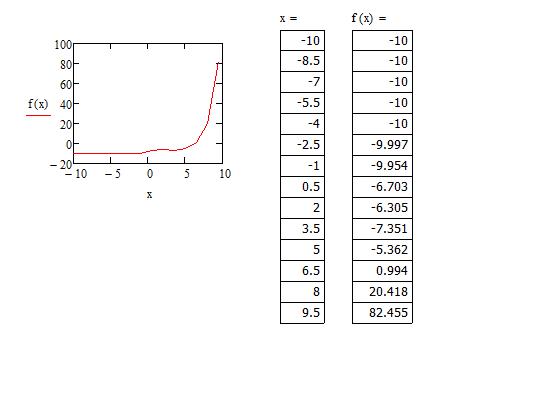
- Для удобства можем отобразить получившиеся значения «х» и «у». Для первого случая используем математическую формулировку «х=», а для второго — «f(x)». Наблюдаем два столбика с соответствующими значениями.
- Построим график, используя сочетание клавиш Shift + 2.
Заметим, что та часть графика, которая устремлялась вверх, исчезла, а на месте нее образовалась непрерывная функция. Все дело в том, что в первом построении функция претерпевала разрыв в некой точке. Второй график был построен по точкам, но, очевидно, что точка, которая не принадлежала графику, не отображена здесь — это одно из особенностей построения графиков по принципу точек.
Видео:MathCAD. Given - FindСкачать

Табуляция графика
Чтобы избавится от ситуации, где функция претерпевает разрыв, необходимо протабулировать график в «Маткаде» и его значения.
- Возьмем известный нам интервал от -10 до 10.
- Теперь запишем команду для переменного диапазона — x:=a,a + 1 .. b (не стоит забывать, что двоеточие — результат нажатия клавиши «;»).
- Смотря на заданную функцию, можно сделать вывод о том, что при значении «х=1» будет происходить деление на ноль. Чтобы без проблем протабулировать функцию, стоит исключить эту операцию так, как показано на картинке.
- Теперь можно наглядно отобразить значения в столбиках, как мы это делали с построением по точкам. Табуляция выполнена, теперь все значения с шагом в одну единицу соответствуют своим аргументам. Обратите внимание, что на «х=1» значение аргумента не определенно.
Видео:Средство для решения систем уравнений в MathCAD 14 (29/34)Скачать

Минимум и максимум функции
Чтобы найти минимум и максимум функции на выбранном участке графика в «Маткаде», следует использовать вспомогательный блок Given. Применяя этот блок, необходимо задать интервал поиска и начальные значения.
Видео:Mathcad. Как задать функциюСкачать
Графический способ решения систем алгебраических уравнений с использованием программного пакета MathCAD
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Графический способ решения систем алгебраических уравнений
с использованием программного пакета Mat h CAD
Автор работы : Сенашева Юлия Викторовна, ученица 7 класса
Научный руководитель : Несивкина Галина Анатольевна
учитель математики первой квалификационной категории.
Учреждение : МБОУ «Ширинская» средняя общеобразовательная школа №18
Ширинского района Республики Хакасия.
1.1.Алгоритм построения графика линейного уравнения с помощью MathCAD;……4
1.2. Исследование расположения прямой, в зависимости от изменения значения k,
в программе MathCAD . 5.
1.3 Алгоритм графического метода решения систем линейных уравнений
с помощью программы MathCAD………………………………………………………6
Актуальность работы : При изучении следующих разделов математики: взаимное расположение графиков линейных функций , графический способ решения системы линейных уравнений столкнулась с тем, что для глубокого исследования этих тем ,отводиться мало времени. Считаю, что изучение этого материала требует более детального рассмотрения, так как он прослеживается в различных заданиях повышенной сложности, в задачах математических олимпиад , в заданиях на ОГЭ, на ЕГЭ и вступительных экзаменов в Высшие Учебные Заведения.
Мотивация : как увеличить время на изучение тем: взаимное расположение графиков линейных функций, графический способ решения системы линейных уравнений.
Проблема: необходимо найти удобный , наглядный, а самое главное быстрый способ построения графиков уравнений.
Гипотеза : объект исследования «Линейная функция» ( А.Г.Мордкович ,Алгебра 7 класс,глава2),»Системы двух линейных уравнений с двумя переменными» (глава3).
Цель работы : показать графический способ решение систем алгебраических уравнений с применением популярного инженерного программного пакета MathCAD. Исследование предоставляет базовые знания работы с программой MathCAD, как они могут быть применены для решения системы двух линейных уравнений с двумя переменными графическим методом.
Результаты исследования : в процессе исследования:
-из множества программ, позволяющих рисовать графики функций, выполнять построения, была выбрана MathCAD , которая является средой визуального программирования, то есть не требует знания специфического набора команд. Простота освоения пакета, дружественный интерфейс, относительная непритязательность к возможностям компьютера явились главными причинами того, что именно этот пакет был выбран мной для решения данной проблемы;
-изучила алгоритм построения графика линейного уравнения с помощью программы MathCAD;
-изучила графический метод решения систем линейных уравнений с помощью программы MathCAD и убедилась в том, что графический метод решения системы линейных уравнений имеет большое значение.
С помощью программы MathCAD мною были выполнены все задания из задачника Алгебра 7 класс по этой теме, ряд заданий олимпиадного характера и задания для подготовки к ОГЭ. Я смогла за короткий срок выполнить большой объем учебного материала, причем в очень наглядной и доступной форме.В процессе работы не тратила время на составление таблиц и построение графиков в тетради .Получился большой запас времени на отработку заданий повышенной сложности.
Перспективы: использовать программный продукт MathCAD., для дальнейшего изучения алгебры 7 класса (глава 8,параграф38.) ,решения задач повышенной сложности, решения заданий из ОГЭ.
В данной работе были рассмотрены примеры , каким образом решаются на MathCAD разнообразные математические задачи (решение систем линейных уравнений). Данная работа поможет ученикам быстро освоить основные навыки работы с пакетом MathCAD, а примеры и способы решения помогут их закрепить для решения новых задач.
1.1 Алгоритм построения графика линейного уравнения с помощью программы MathCAD;
№ 7.17. На координатной плоскости хОу постройте график уравнения:
1.Задать функцию, приведенную выше. Вставить оператор абсолютного значения
2.На вкладке Графики в группе Кривые щелкнуть Вставить график , а затем выбрать График ХУ .
Появиться пустой пустой график
3.В местозаполнителе оси У ,в левой или правой части ввести функцию у = -х+4.
4.В местозаполнителе оси Х внизу графика ввести х. Нажать клавишу «Ввод», появиться линейная кривая.
№ 8.28. Постройте график линейной функции у = х+4 и у=2х
а) координаты точек пресечения графика с осями координат;
б) значение у, соответствующее значению х=—2;-1;1.
в ) значение х ,которому соответствует значение у, равное-2;2;4.
1.Задать функцию, приведенную выше. Вставить оператор абсолютного значения
2.На вкладке Графики в группе Кривые щелкнуть Вставить график , а затем выбрать График ХУ
Появиться пустой график.
3.В местозаполнителе оси У ,в левой или правой части ввести функцию у = х+4.
4.В местозаполнителе оси Х внизу графика ввести х. Нажать клавишу «Ввод», появиться линейная
5.Установить курсор справа от функции. Щелкнуть Добавить кривую .
Появиться новый местозапонитель оси У под текущим местозаполнителем
.
А ) Найти координаты точек пресечения графика с осями координат.
На графике точки пересечения: х=0,у=- 4
Б) Найти значение у, соответствующее значению х = —2;-1;1.
В) Найти значение х ,которому соответствует значение у, равное-2;2;4.
Внесем данные и получим следующее распределение по столбцам .
1.2. Исследование расположения прямой, в зависимости от изменения значения k, в программе MathCAD;
у=3х+4, у=3х, у = -3х,у=2х, у=3х-4,
1.3.Алгоритм графического метода решения систем линейных уравнений с помощью программы MathCAD;
№ 11.10 .Решить графически систему уравнений (задачник Алгебра7 класс, часть 2)
Ответ: система имеет одно решение (2;2)
Пример1.Решить систему уравнений
Ответ: система не имеет решений
Решить систему уравнений
Ответ: система имеет бесконечно много решений.
Вывод : графический метод решения системы линейных уравнений имеет большое значение. С его помощью можно сделать следующие важные выводы:
— графиком обоих уравнений системы линейных уравнений являются прямые;
-эти прямые могут пересекаться, причем только в одной точке,- это значит, что система имеет единственное решение;
-эти прямые могут быть параллельны — это значит, что система не имеет решений( система несовместна);
-эти прямые могут совпасть — это значит, что система имеет бесконечно много решений (система не определена).
Видео:Пример решения системы уравнений в MathCAD 14 (34/34)Скачать

MathCAD — это просто! Часть 5. Системы нелинейных уравнений
Добрый день, уважаемые читатели и читательницы, мы с вами продолжаем грызть гранит науки. Делаем мы это с целью — напомню, если кто вдруг успел позабыть — овладеть замечательным математическим пакетом под названием MathCAD. И в прошлый раз мы с вами закончили на решении систем линейных алгебраических уравнений, для простоты также обозначаемых как СЛАУ. Что ж, линейные уравнения — это, конечно же, спору нет, замечательно. Однако на них, к величайшему сожалению многих поколений школьников и студентов, математические задачи далеко не заканчиваются, а даже, я бы сказал, напротив. То есть СЛАУ — это только частный случай систем уравнений, которые могут в обыкновенной вычислительной практике оказаться совсем даже и не линейными, а, напротив, нелинейными (да, именно так их и называют математики). Системы нелинейных уравнений без использования MathCAD или какого-либо другого математического пакета решать обычно не просто трудно, а очень трудно, но в MathCAD подход к ним не слишком отличается от подхода к СЛАУ — в этом вы сейчас получите возможность убедиться лично.
В общем-то, основные аспекты аналитического решения систем уравнений мы с вами уже, по большому счету, обсудили. Когда это мы так лихо успели? А вот именно тогда, когда обсуждали аналитическое решение систем линейных уравнений с помощью оператора solve. Оказывается, все те же методы вполне применимы для решения систем нелинейных уравнений. Тем не менее, чтобы вы лучше их усвоили, повторю еще раз кратко алгоритм их решения с помощью MathCAD’а и приведу небольшой пример решения подобной системы. Давайте попробуем решить следующую систему уравнений: ex + y + z(xyz)1/2 = 0
(x + y+ z)1/2 = c
x +y + cz = 0
Система выглядит несложной, но для того, чтобы решить ее без использования MathCAD’а, даже очень хорошему математику потребуется не такое уж малое количество времени. Естественно, MathCAD с этой системой справится в два счета. Для ее решения создайте матрицу размером 3 на 1 (3 строки, 1 столбец), в которую и поместите уравнения нашей системы. Напомню, что для того, чтобы MathCAD распознавал уравнения как уравнения, знак «равно» нужно нажимать, удерживая клавишу Ctrl. После того, как система будет введена в виде матрицы, найдите на панели Symbolic оператор solve — мы им уже неоднократно пользовались для решения и простых уравнений, и СЛАУ, так что вы, по идее, уже должны были запомнить, где именно он находится. После оператора через запятые укажите переменные, которые входят в нашу систему уравнений — это пусть будут для начала x, y и z. Поскольку при вводе solve с панели Symbolic MathCAD сам добавляет нужную стрелочку для аналитического решения нашей с вами системы уравнений, то больше ничего, в общем-то, делать не нужно — дальше MathCAD будет решать систему. Сколько это времени у него займет, зависит, конечно же, от мощности вашего компьютера, ну и от самой системы. Нашу систему он решит быстро, а вот если поизвращаться и написать какую-нибудь систему тригонометрических и логарифмических уравнений, да еще и с комплексными переменными (о них мы потом еще поговорим отдельно), то решать такое MathCAD может на слабых компьютерах и не один час.
Для чистоты эксперимента поменяем переменные: пусть теперь произвольной константой в нашей системе будет не c, а z. В этом случае нас ожидает совершенно другое, куда как более громоздкое, решение этой самой системы.
Как видите, аналитическое решение систем нелинейных уравнений с помощью MathCAD’а — вещь несложная, только, к сожалению, возможная далеко не всегда. Как обычно, на помощь символьному процессору MathCAD, который опускает в бессилии руки перед сложными системами, спешат численные методы. Вот здесь уже начинаются различия с системами линейных уравнений.
Численное решение нелинейных систем
В целом алгоритм решения систем нелинейных уравнений в MathCAD для пользователя мало чем отличается от него же для СЛАУ. Мы точно так же задаем начальные приближения, пишем «Given», записываем под этим словом наши уравнения и запрягаем функцию Find, которая должна вывести эти самые уравнения на чистую воду. Все точно так же, как тогда, когда мы решали СЛАУ.
Почему же я так пугал вас буквально двумя абзацами выше, говоря о том, что решать системы нелинейных уравнений намного сложнее, чем СЛАУ? Дело в том, что в случае нелинейных уравнений намного сложнее подобрать такие начальные значения, чтобы численное решение сходилось к реальным значениям корней уравнений. Честно говоря, со СЛАУ тоже не всегда все так просто, как я в прошлый раз сказал, однако в крайнем случае можно заставить MathCAD решить СЛАУ аналитически, а затем просто подставить конкретное численное значение какого-нибудь коэффициента. С нелинейными системами такой прием, что называется, «не покатит». Именно поэтому для получения максимального точного решения многих из таких систем придется озадачиться такими вещами, как задание начальных значений для наших переменных.
Первый способ, который я вам предложу, сразу предупреждаю, для людей неленивых. Заключается он в банальном подборе значений переменных собственными руками. То есть для начала берем начальные значения «с потолка» и решаем систему с помощью Find’а. Подставляем значения, выданные этой функцией, в исходные уравнения и смотрим, насколько они похожи на истинные решения. Если уравнения обращаются при подстановке в верные равенства, то все хорошо: либо система была простой, либо в вас дремлет талант подбирателя корней уравнений. Но если равенством после подстановки и близко не пахнет, то придется попотеть. Нужно начать изменять значения начальных приближений для каждой переменной и смотреть, как это отразится на близости выражений, получившихся после подстановки решений в уравнения, к равенствам. Таким нехитрым методом можно за не столь долгое время, как может сначала показаться, добиться хорошего приближения начальных значений к реальным решениям. И, несмотря на явный садомазохистский характер данного метода, он имеет то неоспоримое преимущество, что действует железно на любые системы и любые переменные — было бы терпение.
Второй метод, который я хочу предложить, этим достоинством не обладает, но зато и не требует от пользователя столь деятельного участия в решении. Думаю, вы сами сможете сформулировать главный его недостаток, если я скажу, что с этим методом мы уже сталкивались, и заключается он в построении графиков для уравнений, входящих в систему. Да, главный недостаток — это сложность в применении к системам уравнений, содержащим более трех переменных. Сложно, сами понимаете, изобразить на мониторе компьютера 25-мерное пространство для отображения решений системы с 25-ю переменными. Но для тех систем, которые содержат две или три переменные, построить график мы вполне сможем. Однако для этого сначала нужно научиться строить графики уравнений.
Построение графиков параметрических кривых
Наиболее простым способом построения графика уравнения в MathCAD’е является параметризация входящих в него переменных друг через друга или через какую-то третью переменную. Что это означает? Поясню на примере. Например, у нас есть уравнение окружности x2 + y2 = 5. Если вы попытаетесь записать функцию f(x, y) = x2 + y2 — 5, а потом построить ее график от x или от y, то вас ожидает разочарование. То, что в итоге выдаст на экран MathCAD, будет так же мало похоже на окружность, как сам MathCAD — на пасьянс «Косынка». Придется придумывать что-то другое. Например, можно подобрать такие функции переменной t, которые, будучи возведенными в квадрат, в сумме тоже дадут пять. Естественно, такими функциями будут тригонометрические — синус и косинус от переменной t, помноженные на корень из пяти. Если мы выразим таким образом x и y через t, то мы параметризуем наше уравнение и уже сможем успешно построить график x(t) от y(t) или же y(t) от x(t) — впрочем, в данном случае в силу симметричности это будет уже не столь важно.
Для того, чтобы решить систему уравнений, нужно просто подобным образом параметризовать и второе уравнение. Вполне возможно, что, как и в нашем примере, оно вполне подойдет для того, чтобы банально выразить x через y или наоборот, после чего построение графика окажется особенно простым (см. соответствующий скриншот). Для нахождения начальных приближений достаточно воспользоваться уже знакомой нам с вами трассировкой — само собой, решением будет точка пересечения двух кривых на уравнении. Для того, чтобы получить более точное значение решения, чем предлагает нам трассировка, нужно, конечно же, подставить полученные с ее помощью координаты точки пересечения графиков в численное решение системы перед Given’ом. Последний скриншот иллюстрирует, что графики мы с вами построили правильно, и с его помощью действительно намного легче искать решение системы двух исходных уравнений. А легче хотя бы уже просто потому, что видно, какого количества корней мы вправе ожидать от нашей системы.
Но работа с трехмерными графиками в MathCAD’е не так проста, как с двумерными, поскольку и сама по себе поверхность — более сложный объект, чем кривая. С поверхностями можно ожидать немалого количества не самого приятного рода сюрпризов, так что лучше о них поговорить более подробно. Этим мы с вами и займемся в следующей статье из цикла о MathCAD’е.
Компьютерная газета. Статья была опубликована в номере 17 за 2008 год в рубрике soft
💥 Видео
Работа с MathCad Prime. Построение графиков.Скачать

Числовое решение. Функция root в MathCAD 14 (28/34)Скачать

Mathcad Prime. Урок 2 - Построение графиковСкачать

MathCAD Построение графика поверхности быстрым способомСкачать
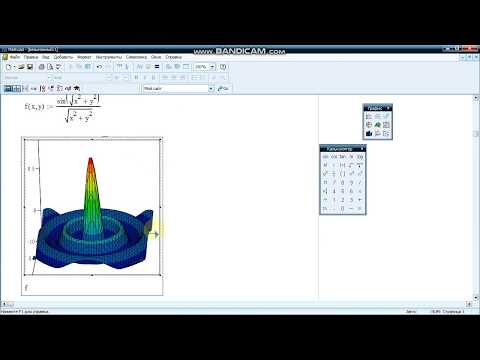
Плоский график функции в MathCAD 14 (10/34)Скачать

Построение графика в Mathcad 14 по точкамСкачать
Как строить графики переходных процессов в программе маткадСкачать

MathCAD Решение системы линейных уравнений матричным методомСкачать
8. MathCad. Решение систем линейных алгебраических уравненийСкачать

MathCAD Решение уравнений с помощью функции root 1 вариантСкачать

MathCAD График функции пользователя с условиемСкачать

Построение трехмерного графика в MathCAD 14 (14/34)Скачать