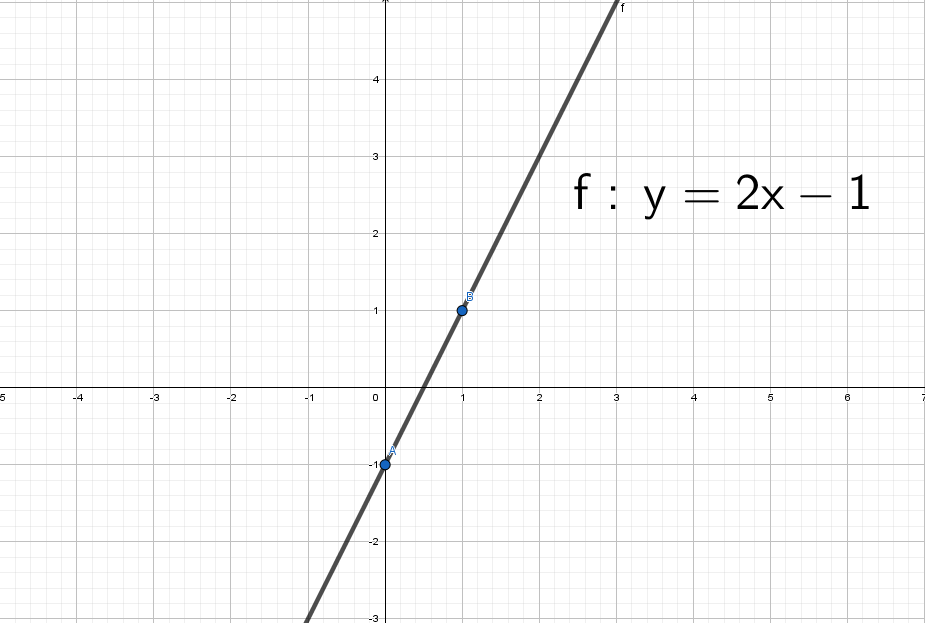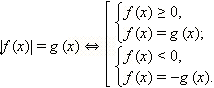Как построить график функции модуля квадратного уравнения (5 видео)

«Графическое решение квадратных уравнений, содержащих модуль». Урок алгебры в 9-м классе

Разделы: Математика

Тема: Графическое решение квадратных уравнений, содержащих модуль.

Цель:

закрепить навыки построения графика квадратичной функции;
научить выполнять преобразования графиков функций;
используя графики функций, решать уравнения.

Содержание

Ход урока
График квадратичной функции с модулем
Описание презентации по отдельным слайдам:
Краткое описание документа:
Графики прямой, параболы, гиперболы, с модулем
💥 Видео

Ход урока

1. Построим график квадратичной функции y = x² – 8x + 12
Преобразуем функцию, выделив полный квадрат, получим y = (x — 4)² — 4
График этой функции получается из графика функции y = x² путем параллельного переноса на вектор

2. Выполним преобразования и построим график функции y = x² – 8|x| +12

Так как противоположным значениям аргумента соответствуют одинаковые значения функции ,то график данной функции будет симметричным относительно оси ординат, поэтому построим график функции y = x² – 8|x| = 12 для x ≥ 0 (т.е. y = x² — 8х + 12) и
отобразим его симметрично относительно оси ординат.

Таким образом, получим:

3. Построим график функции y = | x² – 8|x| + 12 |

График данной функции получим из графика функции y = x² – 8|x| + 12 путем
симметрии относительно оси абсцисс того участка, где у 12;
б) при k = 12;
в) при k = 0;
г) при k = 4;
д) при k (0; 4);
е) при k 15.06.2010

Видео:Задание 23 из ОГЭ Построение графиков функций с модулем | МатематикаСкачать

График квадратичной функции с модулем

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Описание презентации по отдельным слайдам:

График квадратичной функции, содержащей переменную под знаком абсолютной величины. Знание только тогда знание, когда оно приобретено усилиями своей мысли, а не памятью. Л. Н. Толстой. Выполнила: Асламурзаева Белла, ученица 9 «А» класса, СОШ №46 им. И .Дзусова Руководитель: Дряева М.Г. Преподаватель математики СОШ №46 им. И .Дзусова

Содержание: 1.Введение 2.Основные определения и свойства. 3.Построение графика квадратичной функции, содержащей переменную под знаком модуля. 4.Выводы. 5. Используемая литература.

Цель работы – рассмотреть построение графика квадратичной функции, содержащей переменную под знаком модуля. Объект исследования: график квадратичной функции. Предмет исследования: изменения графика квадратичной функции в зависимости от расположения знака абсолютной величины. Задачи: 1) Изучить литературу о свойствах абсолютной величины и квадратичной функции. 2) Исследовать изменения графика квадратичной функции в зависимости от расположения знака абсолютной величины. Практическая значимость моей работы заключается: 1) в использовании приобретенных знаний по данной теме, а также углубление их и применение к другим функциям и уравнениям; 2) в использовании навыков исследовательской работы в дальнейшей учебной деятельности.

Основные определения и свойства Функция, определяемая формулой у=ах²+вх+с, где х и у переменные, а параметры а, в и с – любые действительные числа, причём а≠0, называется квадратичной. Абсолютной величиной неотрицательного числа называется само это число, абсолютной величиной отрицательного числа называется противоположное ему положительное число. Свойства: 1.|a| ≥0, 2. |a|²= a², 3.|a∙b|=|a|∙|b|, 4. |a/b|=|a|/|b|, b≠0

Построение графика линейной функции, содержащей переменную под знаком модуля. 1)f(x)= |x-1|. x = 1- корень подмодульного выражения. Возьмем x=0, (0 1). Вычисляя функции в точках 1,0 и 2,получаем график, состоящий из двух отрезков.

2) f(x)= |x-1|+|x-2|. Вычисляя значение функции в точках 1, 2, 0 и 3, получаем график, состоящий из трех отрезков прямых.

Построение графика квадратичной функции, содержащей переменную под знаком модуля На примере функции у = x ²-6х +5 рассмотрим всевозможные случаи расположения модуля. у = |x 2 – 6х +5| у = | х | 2 – 6х +5 у = х² – 6|х| +5 у = |х|² — 6|х|+5 у = |х² – 6х| +5 у = |х² – 6|х| +5| у = x 2 -|6х + 5| |y|= x 2 – 6х +5

Построим график функции у = |x 2 – 6х +5| Пользуясь определением модуля, рассмотрим два случая: Пользуясь определением модуля, рассмотрим два случая: Пользуясь определением модуля, рассмотрим два случая: Пользуясь определением модуля, рассмотрим два случая: . Выделим все точки параболы с неотрицательной ординатой. . Выделим все точки параболы с неотрицательной ординатой. . Выделим все точки параболы с неотрицательной ординатой. . Выделим все точки параболы с неотрицательной ординатой. . Выделим все точки параболы с неотрицательной ординатой. . Выделим все точки параболы с неотрицательной ординатой. Выделим все точки параболы с неотрицательной ординатой. x ²– 6х +5≥ 0, тогда у= x² – 6х +5.Выделим все точки параболы с неотрицательной ординатой. 2) x² – 6х +5 0, y= -x² + 6х -5.

Рассмотрим график функции у = |х|²– 6х +5 Т.к. |x|²= x² , то функция у = |х|² – 6х +5 совпадает с функцией у = x ²-6х +5 ,а , значит, имеют один и тот же график.

Рассмотрим график функции у = х² – 6|х| +5 Пользуясь определением модуля, рассмотрим два случая: 1)Пусть x≥0, тогда y= х² — 6х +5. Построим параболу у = х² — 6х +5 и обведём ту её часть, которая соответствует неотрицательным значениям х, т.е. часть, расположенную правее оси Оу. 2)Пусть x 0 имеем 2. » onclick=»aa_changeSlideByIndex(14, 0, true)» >

Равенство |y|= x 2 – 6х +5 не задает функции т. к. при x 2 – 6х +5 >0 имеем 2 значения y, соответствующих данному значению x, а при x 2 – 6х +5 0, y= x² – 6х +5 2)при x² – 6х +5

Краткое описание документа:

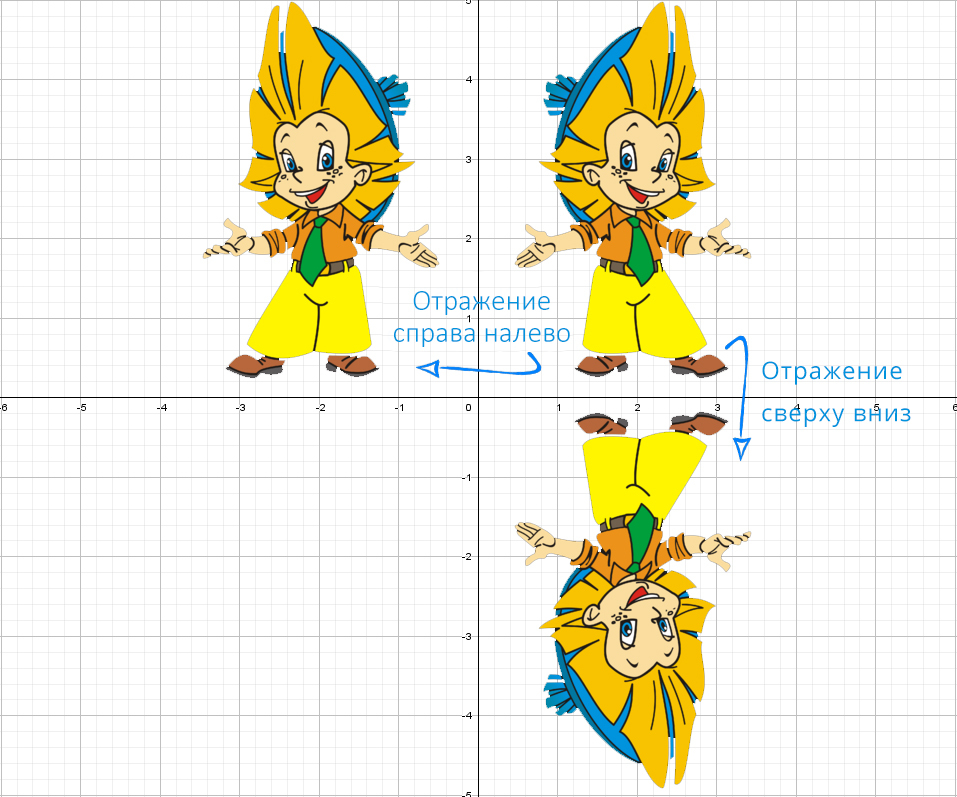
1)Для построения графика функции y = | f ( x )| , надо сохранить ту часть графика функции y = f ( x ), точки которой находятся на оси Ох или выше оси Ох, и симметрично отразить относительно оси Ох ту часть графика функции y = f ( x ), которая расположена ниже оси Ох.

2) Для построения графика y = f (| x |) надо сохранить ту часть графика функции y = f (| x |), точки которой на оси Оу или справа от неё и симметрично отразить эту часть графика относительно оси Оу .

3) Чтобы построить график уравнения | y |= f(x) нужно:

Отбросить ту часть графика , которая лежит ниже оси

Ох, а оставшуюся часть симметрично отобразить

Видео:График квадратичной функции с модулемСкачать

Графики прямой, параболы, гиперболы, с модулем

Пошаговое построение графиков.

«Навешивание» модулей на прямые, параболы, гиперболы.

Графики — самая наглядная тема по алгебре. Рисуя графики, можно творить, а если еще и сможешь задать уравнения своего творчества, то и учитель достойно это оценит.

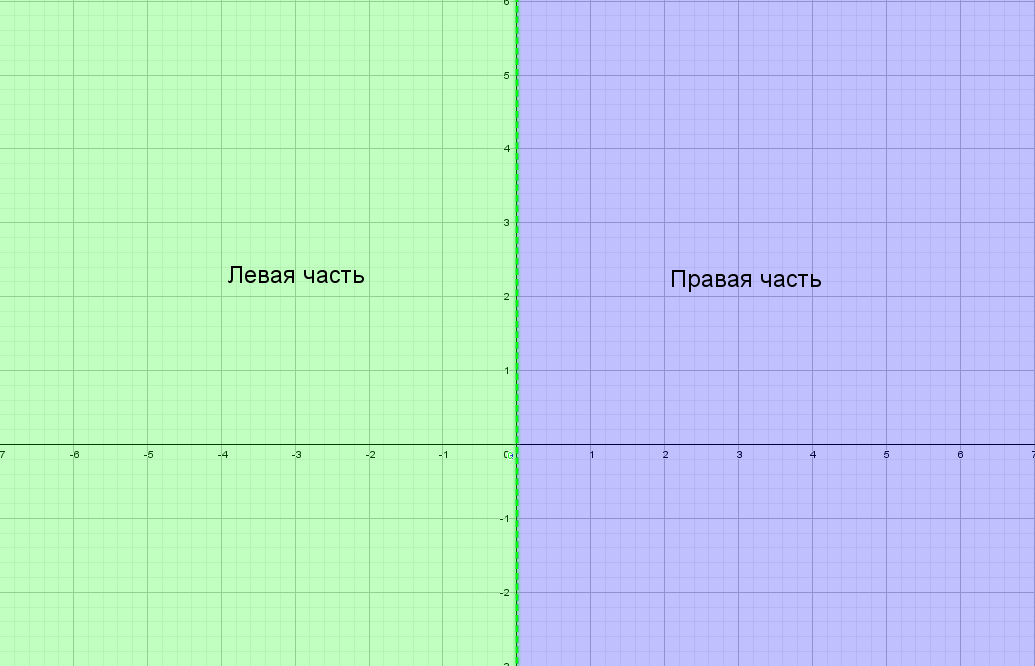
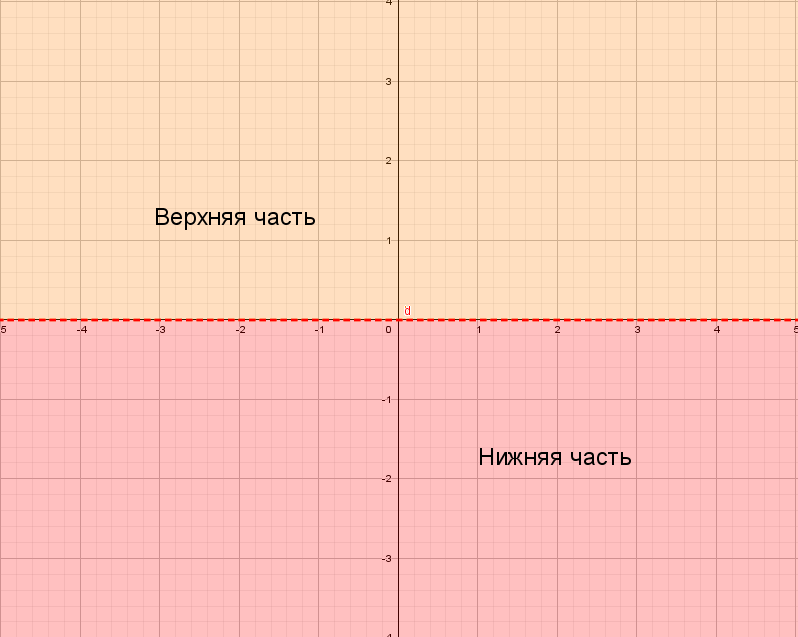
Для понимания друг друга введу немного «обзываний» системы координат:

Для начала построим график прямой y = 2x − 1.

Не сомневаюсь, что ты помнишь. Я напомню себе, что через 2 точки можно провести одну прямую.

Возьмем значение X = 0 и Х = 1 и подставим в выражение y = 2x − 1, тогда соответственно Y = − 1 и Y = 1

Через данные две точки А = (0; −1) и B = (1; 1) проводим единственную прямую:

А если теперь добавить модуль y = |2x − 1|.

Модуль — это всегда положительное значение , получается, что «y» должен быть всегда положительным.

Значит, если модуль «надет» на весь график, то, что было в нижней части «−y», отразится в верхнюю (как будто сворачиваете лист по оси х и то, что было снизу, отпечатываете сверху).

Получается такая зеленая «галочка».

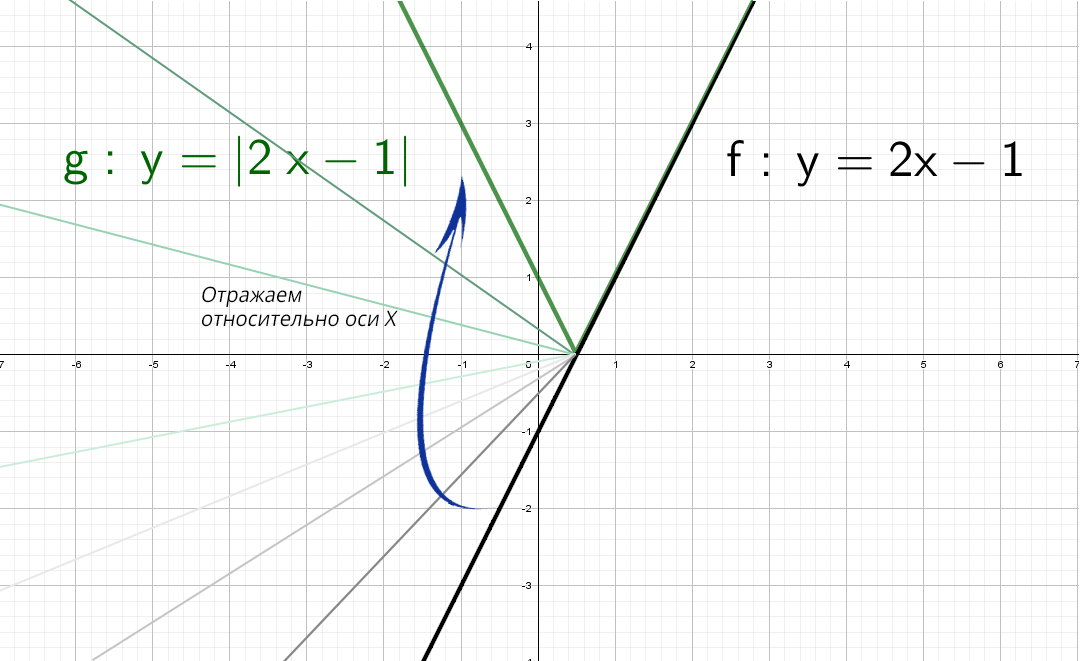
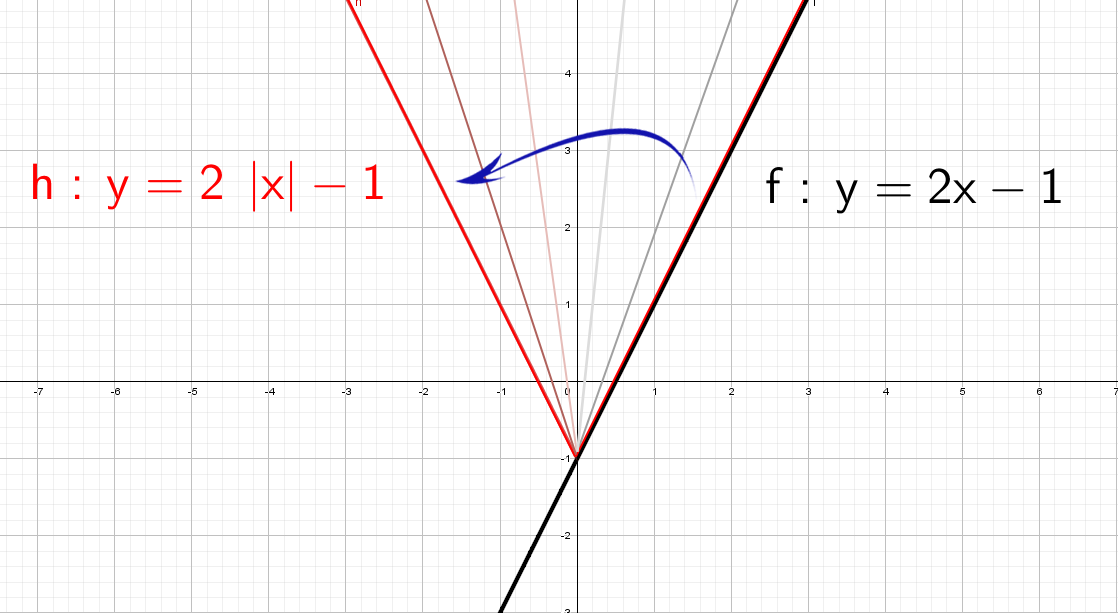
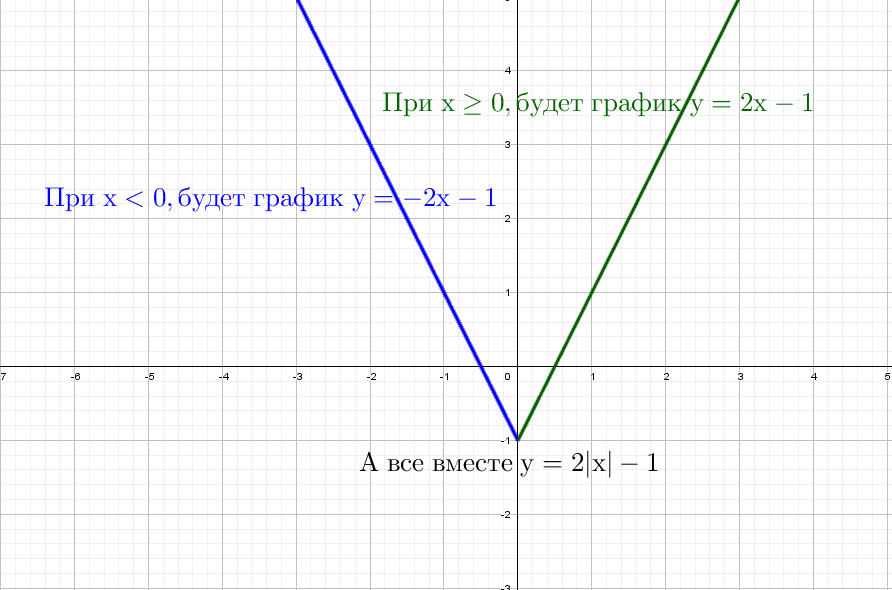
Красота! А как же будет выглядеть график, если надеть модуль только на «х»: y = 2|x| − 1?

Одна строчка рассуждений и рисуем:

Модуль на «x», тогда в этом случае x = −x, то есть все, что было в правой части, отражаем в левую. А то, что было в плоскости «−x», убираем.

Здесь отражаем относительно оси «y» . Такая же галочка, только теперь через другую ось.

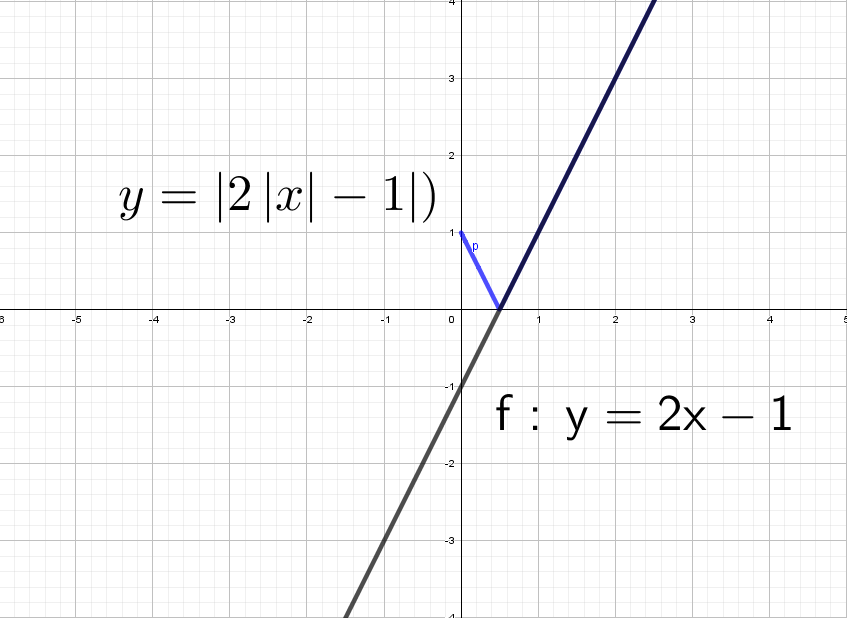
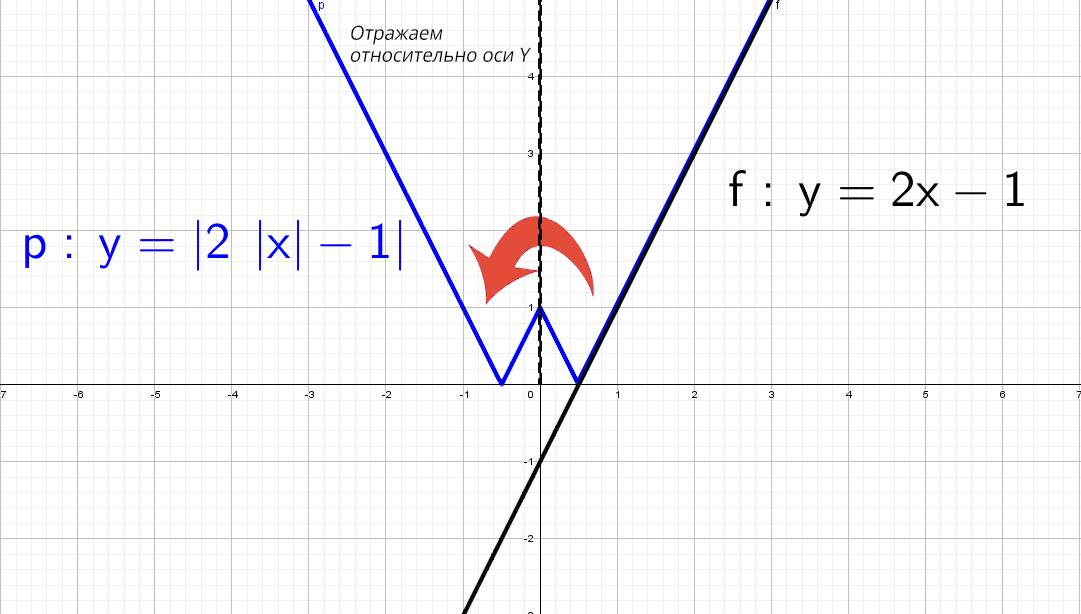
Смертельный номер: y = |2|x| − 1|.

Черную прямую y = 2x − 1 отражаем относительно оси Х, получим y = |2x − 1|. Но мы выяснили, что модуль на х влияет только на левую часть.

В правой части: y = |2x − 1| и y = |2|x| − 1| идентичны!

А после этого отражаем относительно оси «y» то, что мы получили справа налево:

Если ты человек амбициозный, то прямых тебе будет мало! Но то, что описано выше, работает на всех остальных графиках, значит делаем по аналогии.

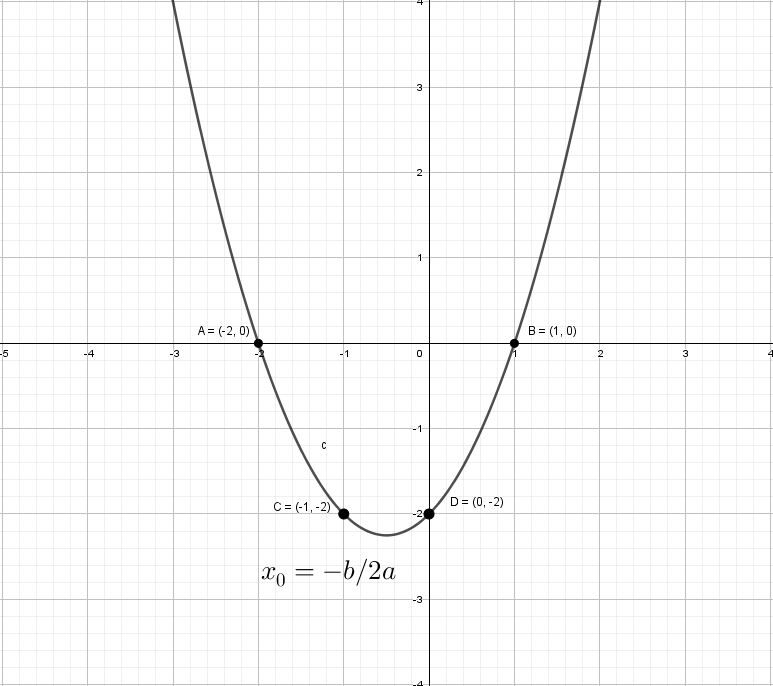
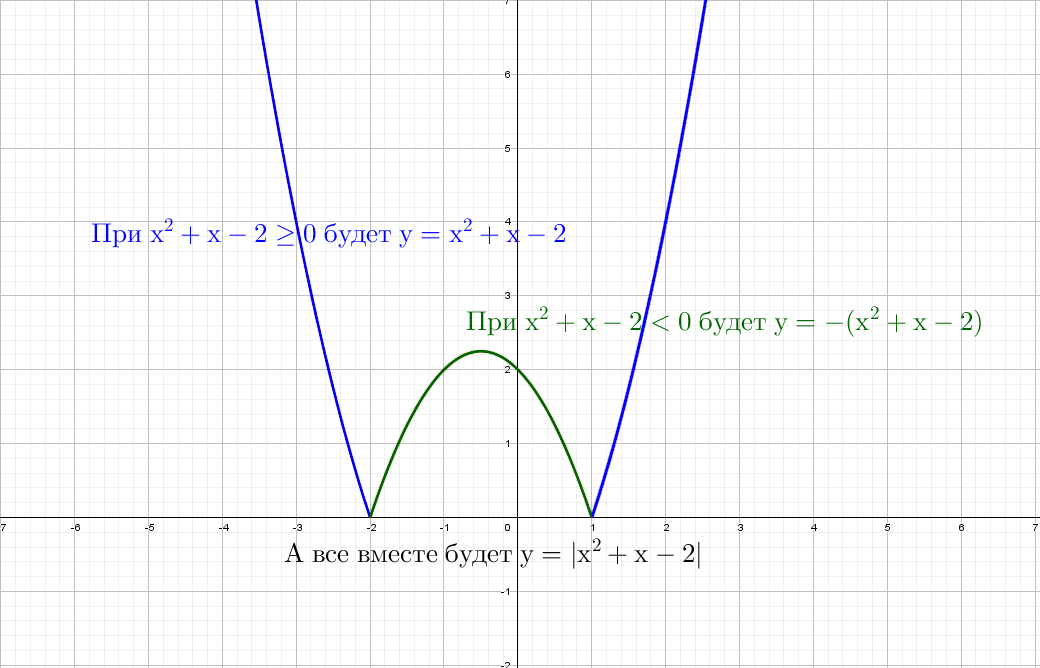
Разберем по винтикам параболу y = x² + x − 2. Точки пересечения с осью «x» получим с помощью дискриминанта: x ₁ = 1 и x ₂ = -2.

Можно найти вершину у параболы и взять пару точек для точного построения.

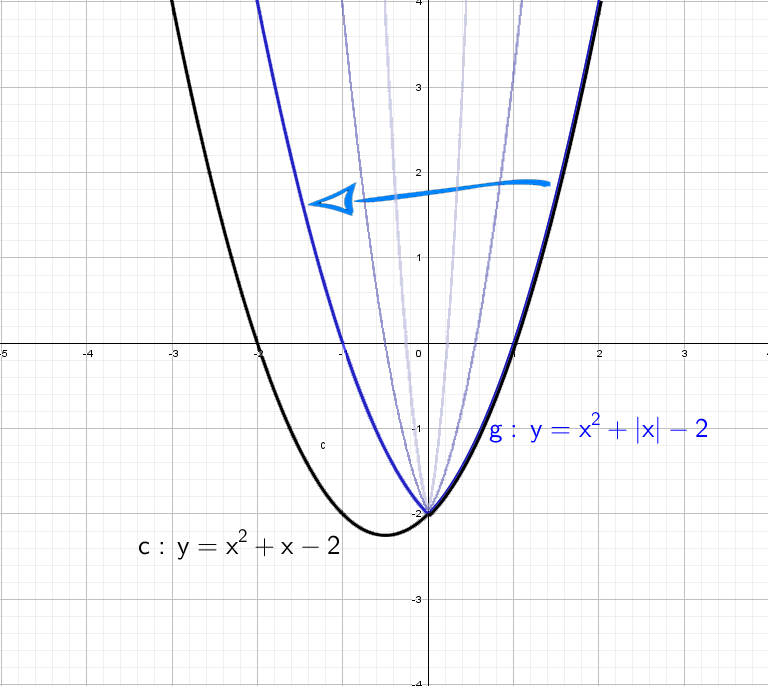
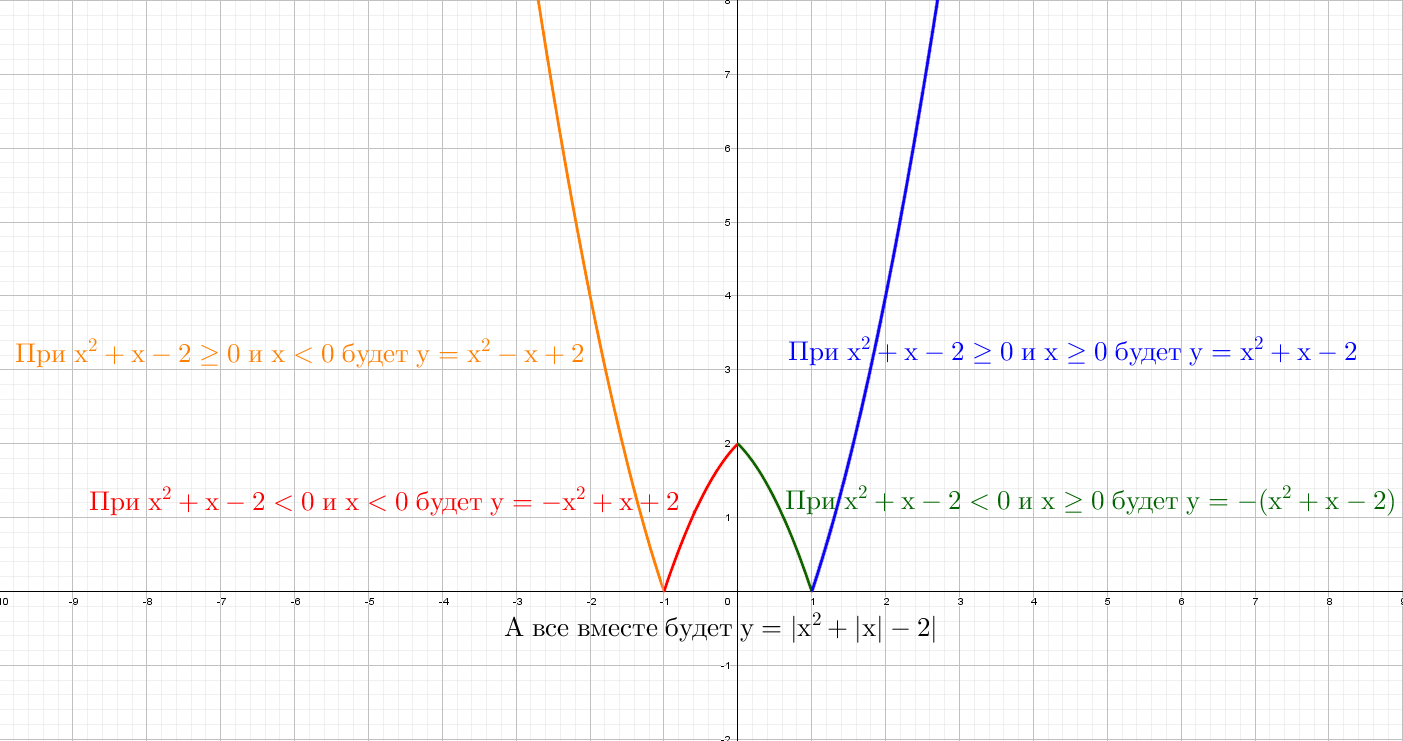
А как будет выглядеть график: y = |x²| + x − 2? Слышу: «Такого мы еще не проходили», а если подумаем? Модуль на x², он же и так всегда положителен, от модуля тут толку, как от стоп-сигнала зайцу − никакого.

При y = x² + |x| − 2 все так же стираем всю левую часть, и отражаем справа налево:

А дальше что мелочиться: рассмотри сразу остальные графики с модулем!

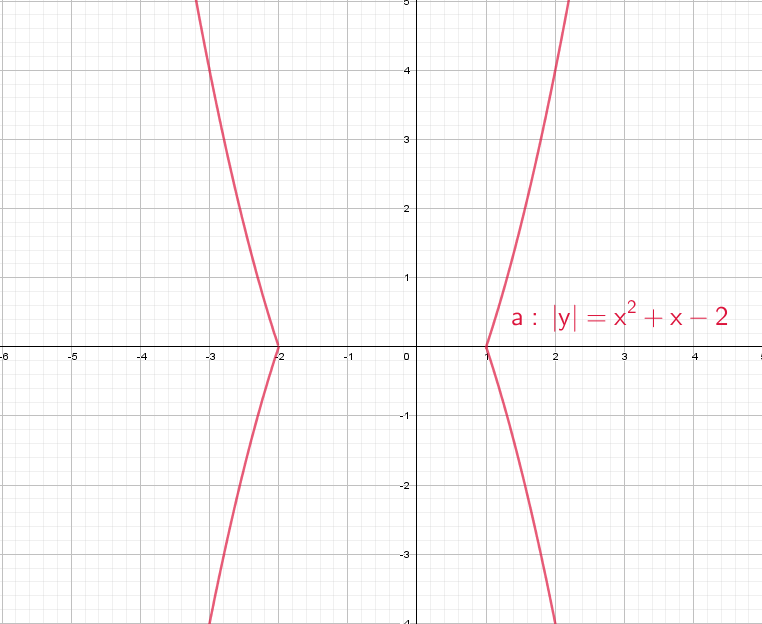
Следующий смертельный номер: |y| = x² + x − 2, подумай хорошенько, а еще лучше попробуй нарисовать сам.

При положительных значениях «y» от модуля нет смысла − уравнения y = x² + x − 2, а при «−y» ничего не меняется, будет так же y = x² + x − 2!

Рисуем параболу в верхней части системы координат (где у > 0), а затем отражаем вниз.

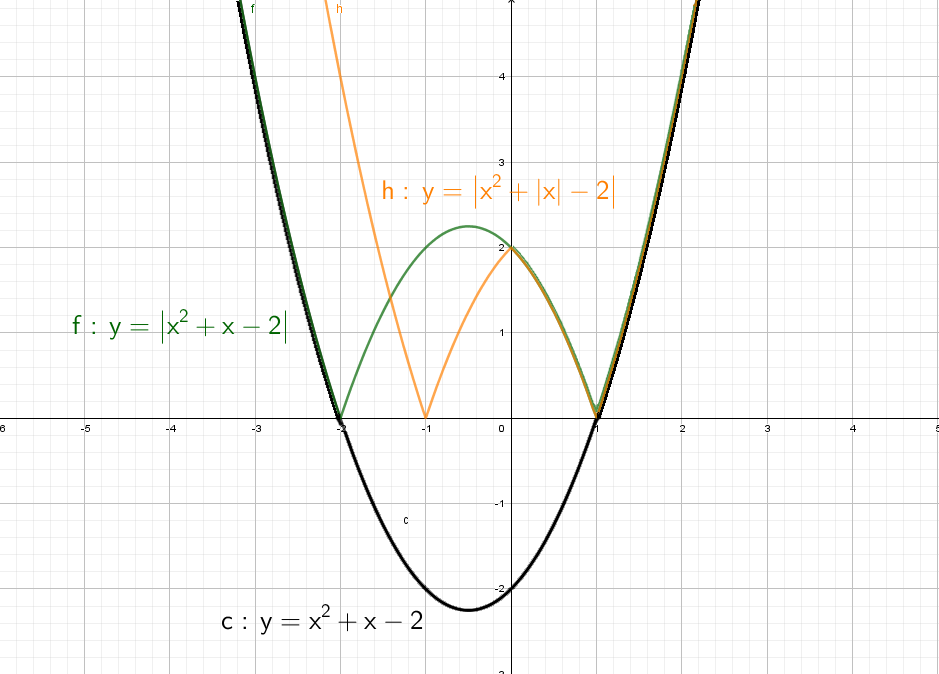
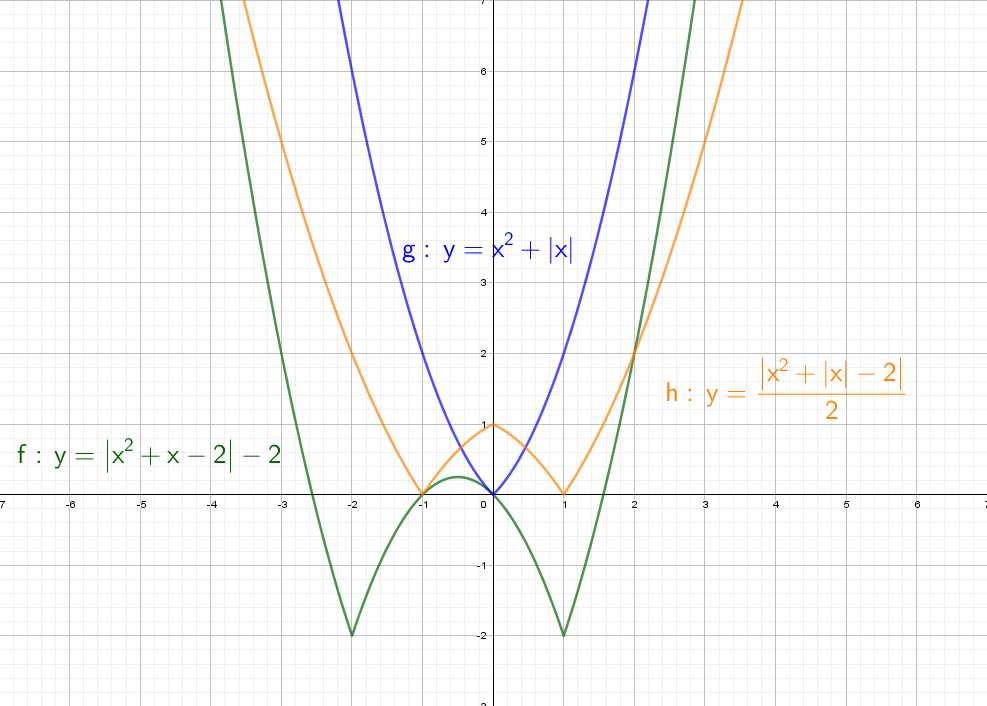
А теперь сразу комбо:

Cиний: похож на y = x² + |x| − 2, только поднят вверх. Строим график в правой части, а затем отражаем через ось Y влево.

Оранжевый: строим в правой части и отражаем относительно оси Х. Доходим до оси Y и отражаем все что было справа налево. Двойка в знаменателе показывает, что график будет «шире», расходится в бока он быстрее остальных.

Зеленый: Так же начинаем с правой части и отражаем относительно оси оси Y. Получается график y = |x² + x − 2|, но еще есть −2, поэтому опустим график на 2 вниз. Теперь параболы как бы отражается относительно Y = − 2.

Легкий и средний уровень позади, и настала пора выжать концентрацию на максимум , потому что дальше тебя ждут гиперболы, которые частенько встречаются во второй части ЕГЭ и ОГЭ.

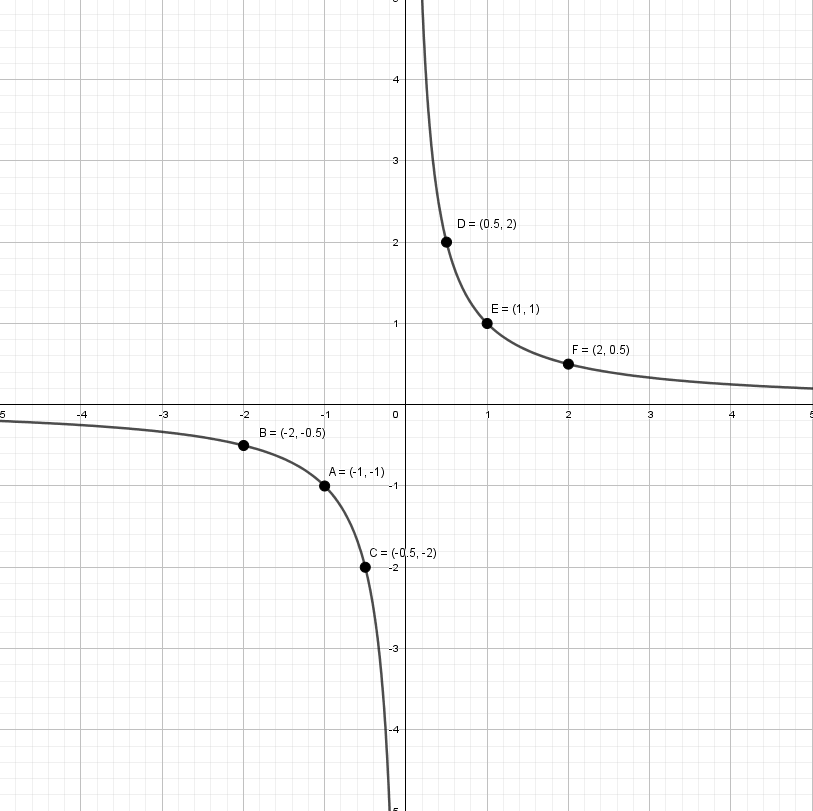
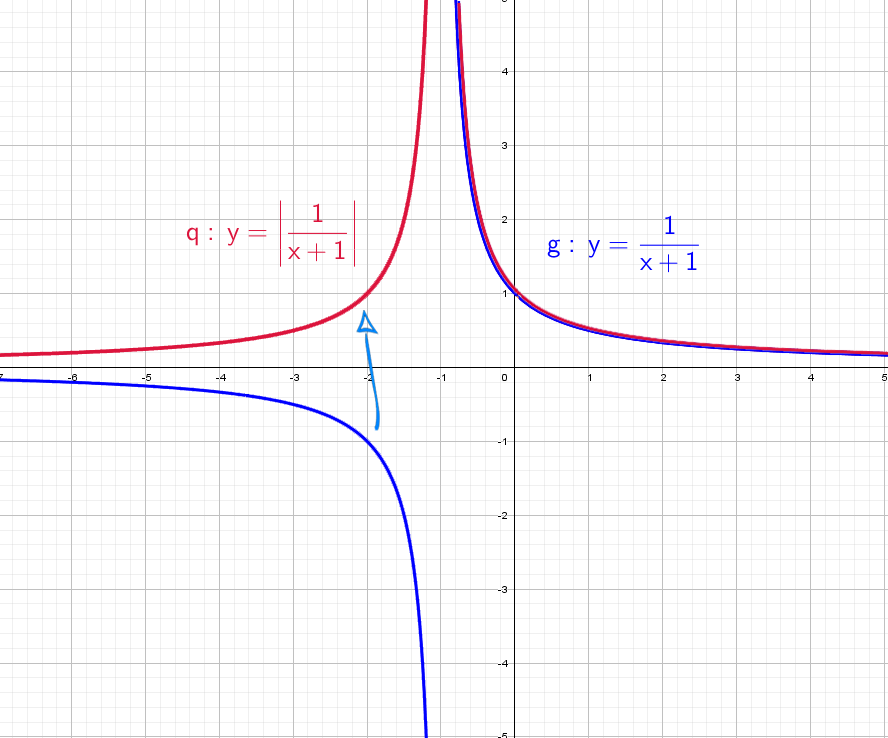
y = 1/x — простая гипербола, которую проще всего построить по точкам, 6-8 точек должно быть достаточно:

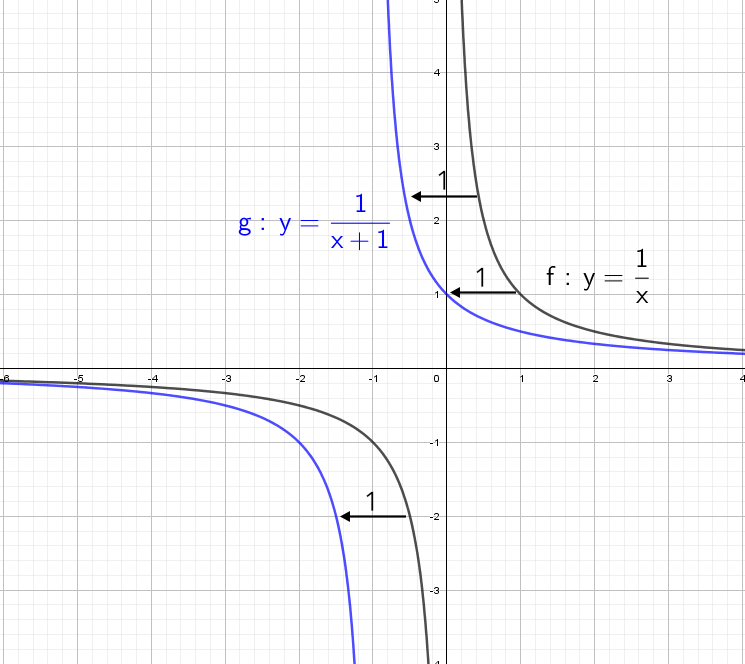
А что будет, если мы добавим в знаменателе «+1»? График сдвинется влево на единицу:

А что будет, если мы добавим в знаменателе « − 1»? График сдвинется вправо на единицу.

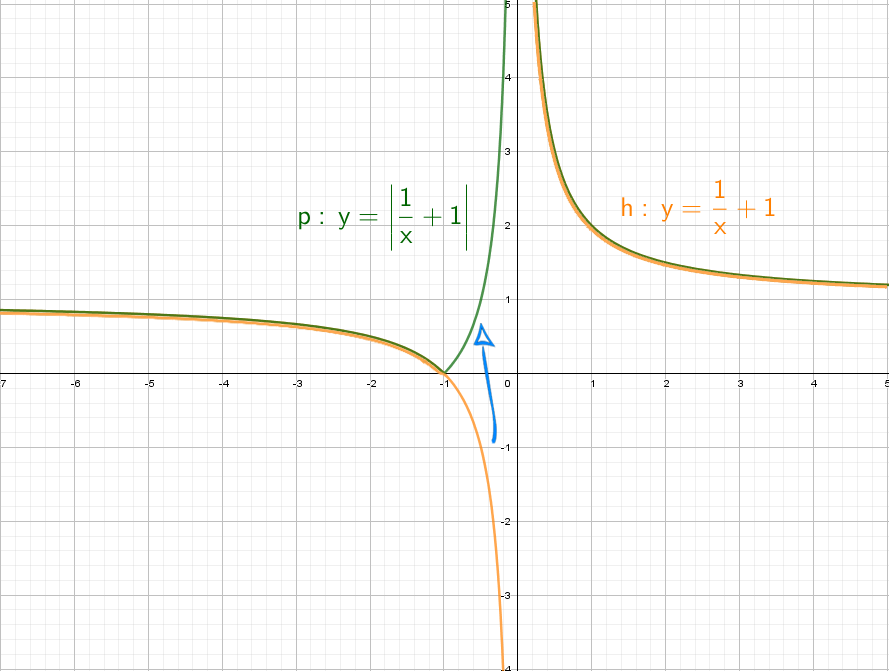
А если добавить отдельно «+1» y = (1/x) + 1? Конечно, график поднимется вверх на единицу!

Глупый вопрос: а если добавить отдельно «−1» y = (1/x) − 1? Вниз на единицу!

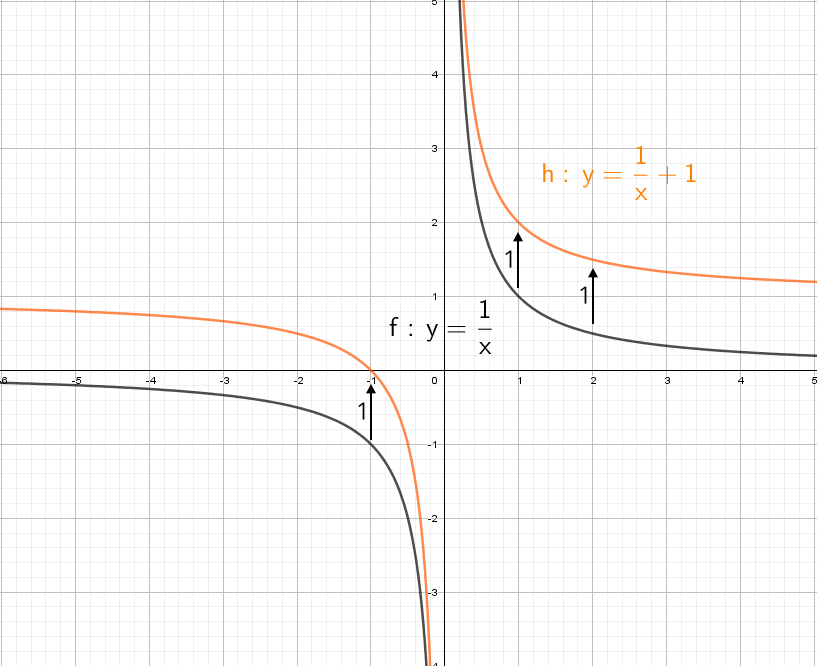
Теперь начнем «накручивать» модули: y = |1/x + 1| — отражаем все из нижней части в верхнюю.

Возьмем другой модуль, мой амбициозный друг, раз ты дошел до этогог места: y = |1/(x + 1)|. Как и выше, когда модуль надет на всю функцию, мы отражаем снизу вверх.

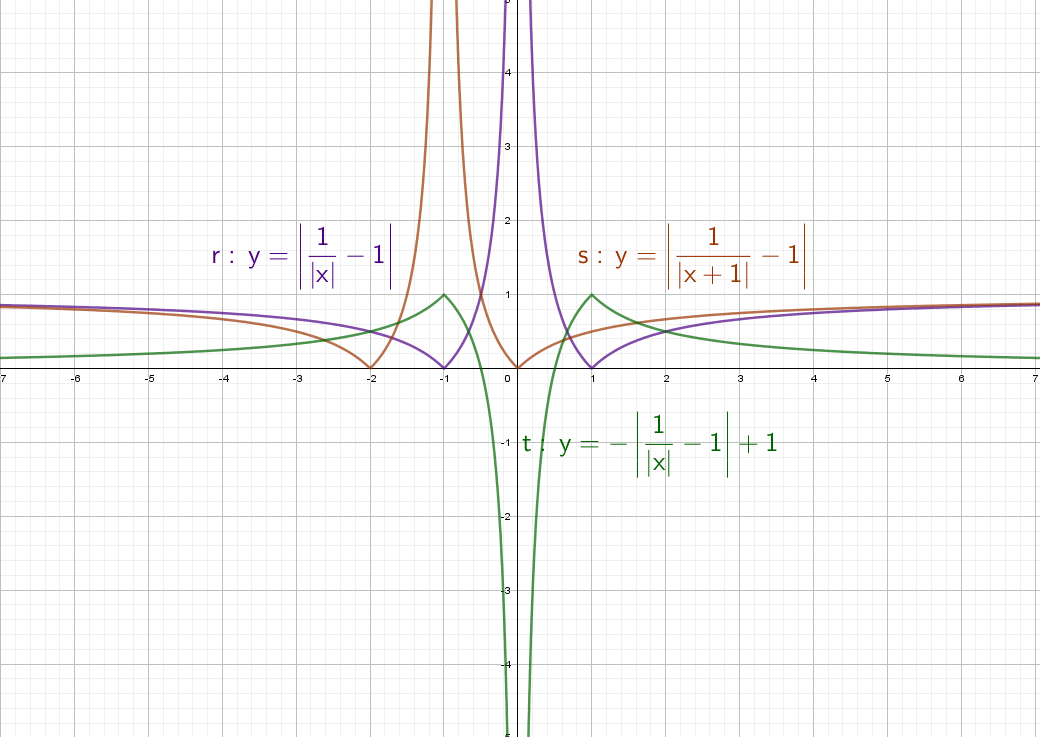
Можно придумывать массу вариантов, но общий принцип остается для любого графика. Принципы повторим в выводах в конце статьи.

Фиолетовый: Вычитаем из дроби −1 и сдвигаем график вниз на единицу. Ставим модуль − отражаем все, что снизу вверх.

Оранжевый: Ставим +1 в знаменателе и график смещается влево на единицу. Вычитаем из дроби −1 и сдвигаем график вниз на единицу. А после этого ставим модуль − отражаем все, что снизу вверх.

Зеленый: Сначала получим фиолетовый график. После этого ставим «−» и отражаем график по горизонтали. Сгибаем лист по оси Х и переводим его вниз. Остается добавить +1, это значит, что его нужно поднять вверх на единицу.

Модули не так уж страшны, если еще вспомнить, что их можно раскрыть по определению:

И построить график, разбив его на кусочно-заданные функции.

Например для прямой:

Для параболы с одним модулем будет два кусочно-заданных графика:

C двумя модулями кусочно-заданных графиков будет четыре:

Таким способом, медленно и кропотливо можно построить любой график!

Модуль — это не просто две палочки, а жизнерадостное, всегда положительное значение!
Модулю без разницы находится он в прямой, параболе или еще где-то. Отражения происходят одни и те же.
Любой нестандартный модуль можно разбить на кусочно-заданные функции, условия только вводятся на каждый модуль .
Существует большое количество модулей, но парочку вариантов стоит запомнить, чтобы не строить по точкам:

Если модуль «надет» на все выражение (например, y = |x² + x − 2|), то нижняя часть отражается наверх.
Если модуль «надет» только на х (например, y = x² + |x| − 2), то правая часть графика отражается на левую часть. А «старая» левая часть стирается.
Если модуль «надет» и на х, и на все выражение (например, y = |x² + |x| − 2|), то сначала отражаем график снизу вверх, после этого стираем полностью левую часть и отражаем справа налево.
Если модуль «надет» на y (например, |y| = x² + x − 2), то мы оставляем верхнюю часть графика, нижнюю стираем. А после отражаем сверху вниз.