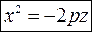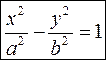Как построить гиперболический параболоид по уравнению

Каноническое уравнение имеет вид ,

где и — это параметры параболоида, ; ,

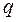
Строим методом сечений.

1) Находим линию пересечения с плоскостью .

Решаем систему уравнений

— это уравнение параболы, симметричной относительно оси .

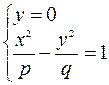
2) Находим линию пересечения с плоскостью .

Решаем систему уравнений

— это уравнение параболы,

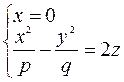
симметричной относительно оси .

3) Находим линии пересечения с плоскостями, параллельными

плоскости .

а) Решаем систему уравнений

— это уравнение гиперболы, у которой

— действительная полуось, а — мнимая полуось.

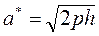
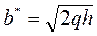
б) Решаем систему уравнений

( знак левой части изменился, так как по условию)

— это уравнение гиперболы, у которой — действительная полуось, а — мнимая полуось.

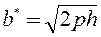
4) Находим линию пересечения с плоскостью .

Решаем систему уравнений

— это уравнение двух прямых, проходящих через точку .

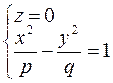
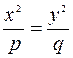
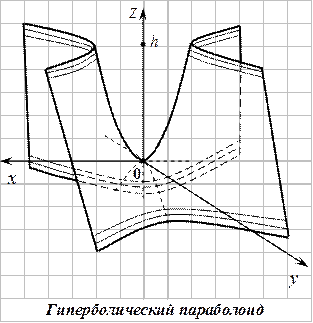
Гиперболический параболоид–это поверхность, имеющая вид седла.

Конус второго порядка

Каноническое уравнение имеет вид

Строим методом сечений.

1) Находим линию пересечения с плоскостью .

Решаем систему уравнений

— это уравнение точки .

2) Находим линии пересечения с плоскостями параллельными .

Решаем систему уравнений

— это уравнение эллипса

с полуосями и .

3) Находим линию пересечения с плоскостью .

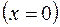
Решаем систему уравнений

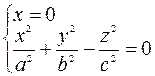
— это уравнение двух прямых, проходящих через начало координат.

4) Находим линию пересечения с плоскостью .

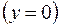
Решаем систему уравнений

— это уравнение двух прямых, проходящих через начало координат.

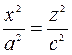
Цилиндрические поверхности

; образующая параллельна оси ;

; образующая параллельна оси ;

; образующая параллельна оси ;

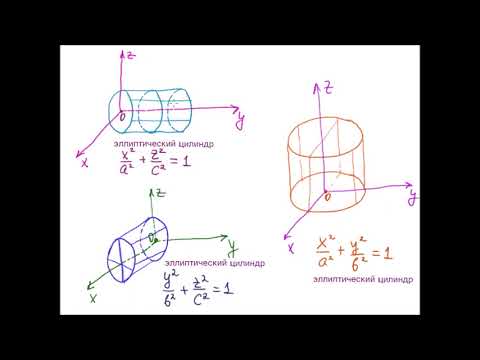
1. Эллиптический цилиндр

образующая параллельна оси

2. Параболический цилиндр

образующая параллельна оси

3. Гиперболический цилиндр

образующая параллельна оси .

Пример 1. Построить поверхность

заданную .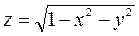

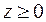
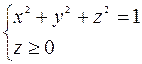
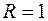
¦ Из уравнения следует, что . Возведем обе части уравнения в квадрат полусфера, ,

с центром в точке . ˜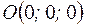

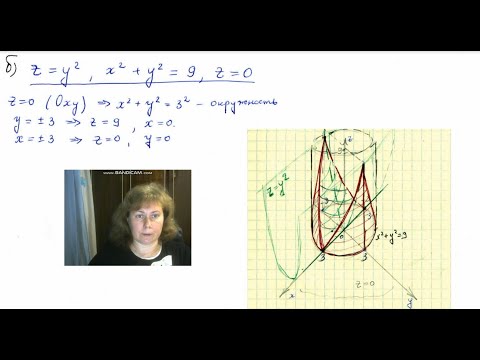
Пример 2. Построить тело, ограниченное поверхностями

.

¦ Определим вид поверхностей.

— параболический цилиндр ;

— плоскость;

— координатные плоскости. ˜

ЛИТЕРАТУРА

1. Шипачев В.С. Основы высшей математики [Текст]: Учебное пособие / В.С.Шипачев, 2002. — 479с.

2. Ильин В.А. Аналитическая геометрия [Текст]: Учебник / В.А.Ильин, Э.Г. Позняк, 2002. — 240с.

3. Зимина О.В. Линейная алгебра и аналитическая геометрия [Текст]: Учебный комплекс: Учебное пособие / О.В.Зимина; Под ред. А.И.Кириллова, 2000. – 328с.

4. Сборник задач по математике для втузов. В 4-х ч [Текст]: Учебное пособие для втузов. Ч.1 / Ред. А.В.Ефимов, Ред. А.С.Поспелов, 2003. – 288с.

5. Данко П.Е. Высшая математика в упражнениях и задачах [Текст]: Учебное пособие в 2-х ч. Ч.2 / П.Е.Данко, А.Г.Попов, Т.Я.Кожевникова, 2005. – 404с.

6. Руководство к решению задач по высшей математике [Текст]: Учебное пособие в 2-х ч. Ч.1 /Е.И.Гурский, В.П.Домашов, В.К.Кравцов, А.П.Сильванович; Под общ. Ред. Е.И.Гурского, 1989. – 349 с.

Видео:Аналитическая геометрия, 8 урок, Поверхности второго порядкаСкачать

Параболоиды: определение, виды, сечения

Видео:Построение гиперболического параболоидаСкачать

Определение параболоида

Эллиптическим параболоидом называется поверхность, определяемая в некоторой прямоугольной системе координат каноническим уравнением

Гиперболическим параболоидом называется поверхность, определяемая в некоторой прямоугольной системе координат каноническим уравнением

В уравнениях (4.51) и (4.52) и — положительные параметры, характеризующие параболоиды, причем для эллиптического параболоида .

Начало координат называют вершиной каждого из параболоидов ((4.50) или (4.51)).

Видео:Поверхности второго порядкаСкачать

Плоские сечения эллиптического параболоида

Плоскость пересекает эллиптический параболоид (4.51) по линии, имеющей в этой плоскости уравнение , которое равносильно уравнению параболы с фокальным параметром . Сечение параболоида плоскостью получаем, подставляя в уравнение (4.51): . Это уравнение равносильно уравнению параболы с фокальным параметром . Эти сечения называются главными параболами эллиптического параболоида (4.51).

Рассмотрим теперь сечение эллиптического параболоида плоскостями, параллельными плоскости . Подставляя , где — произвольная постоянная (параметр), в уравнение (4.51), получаем

При уравнение не имеет действительных решений, т.е. плоскость при не пересекает параболоид (4.51). При уравнению (4.51) удовлетворяет одна вещественная точка — вершина параболоида. При 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADAAAAAQBAMAAACigOGCAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAQSHbWqHAiDGxccHwESbMsvAAAADOSURBVBjTY2DACURTMcUkQITKSwxx51ILIMn4Cl2c6SHDmgsMDOwvINx2BZgEqwEDXwEDA5sBhMuYCpPhSWDgAwryhUwrgMhkCkAk7iUwcD9gYJA7xfgEIsARBpGRS2BgA0rULeB9DrM12AFJYg8DyxO4e4pBMnIbwEa9ZGB/BJPgBUvobWBgfgDyBrMBqlF8G0CuAnqjbwFEhikaYjkn0B8BIG/UqYDdyzgN6lzGFwx+CiA5ncgLYA82wKzyWW4C1A9kgL3cqoAILJcLDADGbCyGJ0mAtgAAAABJRU5ErkJggg==» /> уравнение определяет эллипс с полуосями . Следовательно, сечение эллиптического параболоида плоскостью (при 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADAAAAAQBAMAAACigOGCAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAQSHbWqHAiDGxccHwESbMsvAAAADOSURBVBjTY2DACURTMcUkQITKSwxx51ILIMn4Cl2c6SHDmgsMDOwvINx2BZgEqwEDXwEDA5sBhMuYCpPhSWDgAwryhUwrgMhkCkAk7iUwcD9gYJA7xfgEIsARBpGRS2BgA0rULeB9DrM12AFJYg8DyxO4e4pBMnIbwEa9ZGB/BJPgBUvobWBgfgDyBrMBqlF8G0CuAnqjbwFEhikaYjkn0B8BIG/UqYDdyzgN6lzGFwx+CiA5ncgLYA82wKzyWW4C1A9kgL3cqoAILJcLDADGbCyGJ0mAtgAAAABJRU5ErkJggg==» />) представляет собой эллипс, центр которого лежит на оси аппликат, а вершины — на главных параболах.

Таким образом, эллиптический параболоид можно представить как поверхность, образованную эллипсами, вершины которых лежат на главных параболах (рис.4.46,а).

Видео:Лекция. Гиперболоиды, параболоиды, конус. Исследование методом сечений.Скачать

Параболоид вращения

Эллиптический параболоид, у которого , называется параболоидом вращения . Такой параболоид является поверхностью вращения. Сечения параболоида вращения плоскостями (при 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADAAAAAQBAMAAACigOGCAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAQSHbWqHAiDGxccHwESbMsvAAAADOSURBVBjTY2DACURTMcUkQITKSwxx51ILIMn4Cl2c6SHDmgsMDOwvINx2BZgEqwEDXwEDA5sBhMuYCpPhSWDgAwryhUwrgMhkCkAk7iUwcD9gYJA7xfgEIsARBpGRS2BgA0rULeB9DrM12AFJYg8DyxO4e4pBMnIbwEa9ZGB/BJPgBUvobWBgfgDyBrMBqlF8G0CuAnqjbwFEhikaYjkn0B8BIG/UqYDdyzgN6lzGFwx+CiA5ncgLYA82wKzyWW4C1A9kgL3cqoAILJcLDADGbCyGJ0mAtgAAAABJRU5ErkJggg==» />), представляют собой окружности с центрами на оси аппликат (рис.4.46,б). Его можно получить, вращая вокруг оси параболу , где .

Видео:Поверхности второго порядка. Поверхности вращенияСкачать

Плоские сечения гиперболического параболоида

Сечения гиперболического параболоида координатными плоскостями и представляют собой параболы (главные параболы) или с параметрами или соответственно. Поскольку оси симметрии главных парабол направлены в противоположные стороны, гиперболический параболоид называют седловой поверхностью .

Рассмотрим теперь сечения гиперболического параболоида плоскостями, параллельными плоскости . Подставляя , где — произвольная постоянная (параметр), в уравнение (4.52), получаем При 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADAAAAAQBAMAAACigOGCAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAQSHbWqHAiDGxccHwESbMsvAAAADOSURBVBjTY2DACURTMcUkQITKSwxx51ILIMn4Cl2c6SHDmgsMDOwvINx2BZgEqwEDXwEDA5sBhMuYCpPhSWDgAwryhUwrgMhkCkAk7iUwcD9gYJA7xfgEIsARBpGRS2BgA0rULeB9DrM12AFJYg8DyxO4e4pBMnIbwEa9ZGB/BJPgBUvobWBgfgDyBrMBqlF8G0CuAnqjbwFEhikaYjkn0B8BIG/UqYDdyzgN6lzGFwx+CiA5ncgLYA82wKzyWW4C1A9kgL3cqoAILJcLDADGbCyGJ0mAtgAAAABJRU5ErkJggg==» /> уравнение равносильно уравнению гиперболы полуосями , то есть сечение гиперболического параболоида плоскостью при 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADAAAAAQBAMAAACigOGCAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAQSHbWqHAiDGxccHwESbMsvAAAADOSURBVBjTY2DACURTMcUkQITKSwxx51ILIMn4Cl2c6SHDmgsMDOwvINx2BZgEqwEDXwEDA5sBhMuYCpPhSWDgAwryhUwrgMhkCkAk7iUwcD9gYJA7xfgEIsARBpGRS2BgA0rULeB9DrM12AFJYg8DyxO4e4pBMnIbwEa9ZGB/BJPgBUvobWBgfgDyBrMBqlF8G0CuAnqjbwFEhikaYjkn0B8BIG/UqYDdyzgN6lzGFwx+CiA5ncgLYA82wKzyWW4C1A9kgL3cqoAILJcLDADGbCyGJ0mAtgAAAABJRU5ErkJggg==» /> представляет собой гиперболу с центром на оси аппликат, вершины которой лежат на главной параболе . При получаем уравнение сопряженной гиперболы с полуосями , т.е. сечение гиперболического параболоида плоскостью при представляет собой сопряженную гиперболу с центром на оси аппликат, вершины которой лежат на главной параболе . При получаем уравнение пересекающихся прямых , т.е. сечение гиперболического параболоида плоскостью представляет собой пару пересекающихся в начале координат прямых.

Таким образом, гиперболический параболоид можно представить как поверхность, образованную гиперболами (включая и «крест» из их асимптот), вершины которых лежат на главных параболах (рис.4.47,а).

Сечение параболоида плоскостью , где — произвольная постоянная, представляет собой параболу

равную главной параболе с параметром , вершина которой лежит на другой главной параболе с параметром . Поэтому гиперболический параболоид можно представить как поверхность, получающуюся при перемещении одной главной параболы так, чтобы ее вершина «скользила» по другой главной параболе (рис.4.47,б).

1. Гиперболический параболоид является линейчатой поверхностью, т.е. поверхностью, образованной движением прямой (рис.4.47,в).

2. Ось аппликат канонической системы координат является осью симметрии параболоида, а координатные плоскости — плоскостями симметрии параболоида.

В самом деле, если точка принадлежит параболоиду (эллиптическому или гиперболическому), то точки с координатами при любом выборе знаков также принадлежат параболоиду, поскольку их координаты удовлетворяют уравнению (4.51) или (4.52) соответственно. Поэтому параболоид симметричен относительно координатных плоскостей и координатной оси .

Видео:Образование поверхностей перемещением кривых, 1973Скачать

Поверхности второго порядка

Видео:Гиперболический параболоид. ЧипсыСкачать

Поверхности вращения.

Поверхность (S) называется поверхностью вращения с осью (d), если она составлена из окружностей, которые имеют центры на прямой (d) и лежат в плоскостях, перпендикулярных данной прямой.

Рассмотрим линию (L), которая лежит в плоскости (P), проходящей через ось вращения (d) (рис. 43), и будем вращать ее вокруг этой оси. Каждая точка линии опишет окружность, а вся линия — поверхность вращения.

Рис. 10.1. Поверхность вращения.

Выберем начало декартовой прямоугольной системы координат (O, boldsymbol_, boldsymbol_, boldsymbol_) на оси (d), вектор (boldsymbol_) направим вдоль (d), а вектор (boldsymbol_) поместим в плоскости (P). Таким образом, (O, boldsymbol_, boldsymbol_) — декартова система координат в плоскости (P). Пусть линия (L) имеет в этой системе координат уравнение (f(x, y)=0).

Рассмотрим точку (M(x, y, z)). Через нее проходит окружность, которая имеет центр на оси (d) и лежит в плоскости, перпендикулярной этой оси. Радиус окружности равен расстоянию от (M) до оси, то есть (sqrt<x^+y^>). Точка (M) лежит на поверхности вращения тогда и только тогда, когда на указанной окружности имеется точка Мь принадлежащая вращаемой линии (L).

Точка (M_(x_, y_, z_)) лежит в плоскости (P), и потому (y_=0). Кроме того, (z_=z) и (|x|=sqrt<x^+y^>), так как (M_) лежит на той же окружности, что и (M). Координаты точки (M_) удовлетворяют уравнению линии (L): (f(x_, z_)=0). Подставляя в это уравнение (x_) и (z_), мы получаем условие на координаты точки (M), необходимое и достаточное для того, чтобы (M) лежала на поверхности вращения (S): равенство
$$
fleft(pm sqrt<x^+y^>, zright)=0label
$$
должно быть выполнено хотя бы при одном из двух знаков перед корнем. Это условие, которое можно записать также в виде
$$
fleft(sqrt<x^+y^>, zright)fleft(-sqrt<x^+y^>, zright)=0,label
$$
и является уравнением поверхности вращения линии (L) вокруг оси (d).

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Эллипсоид.

Рассмотрим поверхности, которые получаются при вращении эллипса вокруг его осей симметрии. Направив вектор (boldsymbol_) сначала вдоль малой оси эллипса, а затем вдоль большой оси, мы получим уравнения эллипса в следующих видах:
$$
frac<x^><a^>+frac<z^><c^>=1, frac<z^><a^>+frac<x^><c^>=1.nonumber
$$
(Здесь через (c) обозначена малая полуось эллипса.) В силу формулы eqref уравнениями соответствующих поверхностей вращения будут
$$
frac<x^+y^><a^>+frac<z^><c^>=1, frac<z^><a^>+frac<x^+y^><c^>=1 (a > c).label
$$
Поверхности с такими уравнениями называются соответственно сжатым и вытянутым эллипсоидами вращения (рис. 10.2).

Рис. 10.2. Сжатый (а) и вытянутый (б) эллипсоиды вращения.

Каждую точку (M(x, y, z)) на сжатом эллипсоиде вращения сдвинем к плоскости (y=0) так, чтобы расстояние от точки до этой плоскости уменьшилось в постоянном для всех точек отношении (lambda Рис. 10.3. Эллипсоид.

Эллипсоид так же, как и эллипсоид вращения, из которого он получен, представляет собой замкнутую ограниченную поверхность. Из уравнения eqref видно, что начало канонической системы координат — центр симметрии эллипсоида, а координатные плоскости — его плоскости симметрии.

Эллипсоид можно получить из сферы (x^+y^+z^=a^) сжатиями к плоскостям (y=0) и (z=0) в отношениях (lambda=b/a) и (mu=c/a).

В этой статье нам часто придется прибегать к сжатию, и мы не будем его каждый раз описывать столь подробно.

Видео:Поверхности в Excel (Surface in Excel)Скачать

Конус второго порядка.

Рассмотрим на плоскости (P) пару пересекающихся прямых, задаваемую в системе координат (O, boldsymbol_, boldsymbol_) уравнением (a^x^-c^z^=0). Поверхность, получаемая вращением этой линии вокруг оси аппликат, имеет уравнение
$$
a^(x^+y^)-c^z^=0label
$$
и носит название прямого кругового конуса (рис. 10.4). Сжатие к плоскости (y=0) переводит прямой круговой конус в поверхность с уравнением
$$
a^x^+b^y^-c^z^=0label
$$
называемую конусом второго порядка.

Обратите внимание на то, что левая часть уравнения eqref — однородная функция, и поверхность является конусом в смысле определения, введенного ранее.

Рис. 10.4. Прямой круговой конус.

Видео:Поверхности 2-го порядка | Лекция 14 | ЛинАл | СтримСкачать

Однополостный гиперболоид.

Однополостный гиперболоид вращения — это поверхность вращения гиперболы
$$
frac<x^><a^>-frac<z^><c^>=1nonumber
$$
вокруг той оси, которая ее не пересекает. По формуле eqref мы получаем уравнение этой поверхности (рис. 10.5)
$$
frac<x^+y^><a^>-frac<z^><c^>=1.label
$$

Рис. 10.5. Однополостный гиперболоид вращения.

В результате сжатия однополостного гиперболоида вращения к плоскости (y=0) мы получаем однополостный гиперболоид с уравнением
$$
frac<x^><a^>+frac<y^><b^>-frac<z^><c^>=1.label
$$

Интересное свойство однополостного гиперболоида — наличие у него прямолинейных образующих. Так называются прямые линии, всеми своими точками лежащие на поверхности. Через каждую точку однополостного гиперболоида проходят две прямолинейные образующие, уравнения которых можно получить следующим образом.

Покажем на примере, как найти образующие, проходящие через данную точку поверхности. Рассмотрим поверхность (x^+y^-z^=0) и точку (M_(1, 1, 1)) на ней. Подставляя координаты (M_) в уравнения eqref, мы получаем условия на (lambda) и (mu): (2lambda=2mu) и (0 cdot lambda=0 cdot mu). Первое из них определяет (lambda) и (mu) с точностью до общего множителя, но только с такой точностью они и нужны. Подставляя эти значения в eqref, получаем уравнения прямолинейной образующей
$$
x+z=1+y, x-z=1-y.nonumber
$$

Она проходит через (M_), так как (lambda) и (mu) так и выбирались, чтобы координаты (M_) удовлетворяли этой системе. Аналогично, подставляя координаты (M_) в (10), находим условия на (lambda’) и (mu’): (2mu’=0) и (2mu’=0). Коэффициент (lambda’) можно взять любым ненулевым, и мы приходим к уравнению второй образующей: (x=z), (y=1).

Если вместе с гиперболой мы будем вращать ее асимптоты, то они опишут прямой круговой конус, называемый асимптотическим конусом гиперболоида вращения. При сжатии гиперболоида вращения его асимптотический конус сжимается в асимптотический конус общего однополостного гиперболоида.

Видео:Построение графика "эллиптический параболоид"Скачать

Двуполостный гиперболоид.

Двуполостный гиперболоид вращения — это поверхность, получаемая вращением гиперболы
$$
frac<z^><c^>-frac<x^><a^>=1nonumber
$$
вокруг той оси, которая ее пересекает. По формуле eqref мы получаем уравнение двуполостного гиперболоида вращения
$$
frac<z^><c^>-frac<x^+y^><a^>=1.label
$$
В результате сжатия этой поверхности к плоскости у=0 получается поверхность с уравнением
$$
frac<z^><c^>-frac<x^><a^>-frac<y^><b^>=1.label
$$

Поверхность, которая в некоторой декартовой прямоугольной системе координат имеет уравнение вида eqref, называется двуполостным гиперболоидом (рис. 10.6). Двум ветвям гиперболы здесь соответствуют две не связанные между собой части (“полости”) поверхности, в то время как при построении однополостного гиперболоида вращения каждая ветвь гиперболы описывала всю поверхность.

Асимптотический конус двуполостного гиперболоида определяется так же, как и для однополостного.

Рис. 10.6. Двуполостный гиперболоид вращения.

Видео:Урок 3. 3D-поверхности в excel.Скачать

Эллиптический параболоид.

Вращая параболу (x^=2pz) вокруг ее оси симметрии, мы получаем поверхность с уравнением
$$
x^+y^=2pz.label
$$
Она называется параболоидом вращения. Сжатие к плоскости (y=0) переводит параболоид вращения в поверхность, уравнение которой приводится к виду
$$
frac<x^><a^>+frac<y^><b^>=2z.label
$$

Поверхность, которая имеет такое уравнение в некоторой декартовой прямоугольной системе координат, называется эллиптическим параболоидом (рис. 10.7).

Рис. 10.7. Эллиптический параболоид.

Видео:Видеоурок "Гипербола"Скачать

Гиперболический параболоид.

По аналогии с уравнением eqref мы можем написать уравнение
$$
frac<x^><a^>-frac<y^><b^>=2z.label
$$

Поверхность, которая имеет уравнение вида eqref в некоторой декартовой прямоугольной системе координат, называется гиперболическим параболоидом.

Исследуем форму этой поверхности. Для этого рассмотрим ее сечение плоскостью (x=alpha) при произвольном (alpha). В этой плоскости выберем декартову прямоугольную систему координат (O’, boldsymbol_, boldsymbol_) с началом в точке (O'(alpha, 0, 0)). Относительно этой системы координат линия пересечения имеет уравнение
$$
-frac<y^><b^>=2left(z-frac<alpha^><2a^>right).label
$$
Эта линия — парабола, в чем легко убедиться, перенеся начало координат в точку (O″) с координатами ((0, alpha^/(2a^))). (Координаты этой точки относительно исходной системы координат (O, boldsymbol_, boldsymbol_, boldsymbol_) в пространстве равны ((alpha, 0, alpha^/(2a^))).)

Точка (O″), очевидно, является вершиной параболы, ось параболы параллельна вектору (boldsymbol_), а знак минус в левой части равенства eqref означает, что ветви параболы направлены в сторону, противоположную направлению (boldsymbol_). Заметим, что после переноса начала координат в точку (O″) величина а не входит в уравнение параболы, и, следовательно, сечения гиперболического параболоида плоскостями (x=alpha) при всех (alpha) представляют собой равные параболы.

Будем теперь менять величину (alpha) и проследим за перемещением вершины параболы (O″) в зависимости от (alpha). Из приведенных выше координат точки (O″) следует, что эта точка перемещается по линии с уравнениями
$$
z=frac<x^><2a^>, y=0nonumber
$$
в системе координат (O, boldsymbol_, boldsymbol_, boldsymbol_). Эта линия — парабола в плоскости (y=0). Вершина параболы находится в начале координат, ось симметрии совпадает с осью аппликат, а ветви параболы направлены в ту же сторону, что и вектор (boldsymbol_).

Теперь мы можем построить гиперболический параболоид следующим образом: зададим две параболы и будем перемещать одну из них так, чтобы ее вершина скользила по другой, оси парабол были параллельны, параболы лежали во взаимно перпендикулярных плоскостях и ветви их были направлены в противоположные стороны.

При таком перемещении подвижная парабола описывает гиперболический параболоид (рис. 10.8).

Рис. 10.8. Гиперболический параболоид. (OB) — неподвижная парабола, (KLM, NOP, QRS) — положения подвижной параболы.

Сечения гиперболического параболоида плоскостями с уравнениями (z=alpha) при всевозможных (alpha) — гиперболы. Эти сечения нарисованы на рис. 10.9.

Рис. 10.9. Сечения гиперболического параболоида

Выводятся эти уравнения так же, как и уравнения прямолинейных образующих однополостного гиперболоида.

Рис. 10.10. Прямолинейные образующие гиперболического параболоида

💡 Видео

Практическое занятие: поверхности второго порядкаСкачать

Эллипс, парабола и гипербола. Конические сечения | Ботай со мной #055 | Борис Трушин |Скачать

6 Гиперболический параболоидСкачать

Поверхности 2 порядкаСкачать

Цилиндрические поверхностиСкачать

§23 Построение гиперболыСкачать

Кривые второго порядка. Эллипс. Приведение к каноническому виду и чертежСкачать