Одним из важнейших химических понятий, на котором основываются стехиометрические расчёты, является химическое количество вещества. Количество некоторого вещества X обозначается n(X). Единицей измерения количества вещества является моль.
Моль – это количество вещества, в котором содержится 6,02·10 23 молекул, атомов, ионов или других структурных единиц, из которых состоит вещество.
Масса одного моля некоторого вещества Х называется молярной массой M(X) этого вещества. Зная массу m(X) некоторого вещества X и его молярную массу, можно рассчитать количество этого вещества по формуле:

Число 6,02·10 23 называется числом Авогадро (Na); его размерность моль –1 .
Умножая число Авогадро Na на количество вещества n(X), можно рассчитать число структурных единиц, например, молекул N(X) некоторого вещества X:
По аналогии с понятием молярной массы ввели понятие молярного объёма: молярный объём Vm(X) некоторого вещества X – это объём одного моля этого вещества. Зная объём вещества V(X) и его молярный объём, можно рассчитать химическое количество вещества:

В химии особенно часто приходится иметь дело с молярным объёмом газов. Согласно закону Авогадро в равных объёмах любых газов, взятых при одной и той же температуре и равном давлении, содержится одно и тоже число молекул. При равных условиях 1 моль любого газа занимает один и тот же объём. При нормальных условиях (н.у.) – температура 0°С и давление 1 атмосфера (101325 Па) – этот объём равен 22,4 л. Таким образом, при н.у. Vm(газа) = 22,4 л/моль. Следует особо подчеркнуть, что величина молярного объёма 22,4 л/моль применяется только для газов.
Знание молярных масс веществ и числа Авогадро позволяет выразить массу молекулы любого вещества в граммах. Ниже приводится пример расчёта массы молекулы водорода.
1 моль газообразного водорода содержит 6,02·10 23 молекул H2 и имеет массу 2 г (т.к. M(H2) = 2 г/моль). Следовательно,
6,02·10 23 молекул H2 имеют массу 2 г;
1 молекула H2 имеет массу x г; x = 3,32·10 –24 г.
Понятие «моль» широко используется для проведения расчётов по уравнениям химических реакций, поскольку стехиометрические коэффициенты в уравнении реакции показывают, в каких молярных соотношениях вещества реагируют друг с другом и образуются в результате реакции.
Например, уравнение реакции 4 NH3 + 3 O2 → 2 N2 + 6 H2O содержит следующую информацию: 4 моль аммиака реагируют без избытка и недостатка с 3 моль кислорода, при этом образуется 2 моль азота и 6 моль воды.
Пример 4.1 Рассчитайте массу осадка, образующегося при взаимодействии растворов, содержащих 70,2 г дигидрофосфата кальция и 68 г гидроксида кальция. Какое вещество останется в избытке? Чему равна его масса?
Из уравнения реакции видно, что 3 моль Ca(H2PO4)2 реагирует с 12 моль KOH. Рассчитаем количества реагирующих веществ, которые даны по условию задачи:
n(KOH) = m(KOH) / M(KOH) = 68 г : 56 г/моль = 1,215 моль.
на 3 моль Ca(H2PO4)2 требуется 12 моль KOH
на 0,3 моль Ca(H2PO4)2 требуется х моль KOH
х = 1,2 моль – столько KOH потребуется, для того чтобы реакция прошла без избытка и недостатка. А по условию задачи имеется 1,215 моль KOH. Следовательно, KOH – в избытке; количество оставшегося после реакции KOH:
n(KOH) = 1,215 моль – 1,2 моль = 0,015 моль;
его масса m(KOH) = n(KOH) × M(KOH) = 0,015 моль × 56 г/моль = 0,84 г.
Расчёт образующегося продукта реакции (осадок Ca3(PO4)2) следует вести по веществу, которое находится в недостатке (в данном случае – Ca(H2PO4)2), так как это вещество прореагирует полностью. Из уравнения реакции видно, что число моль образующегося Ca3(PO4)2 в 3 раза меньше числа моль прореагировавшего Ca(H2PO4)2:
Задание №5
а) Рассчитайте химические количества реагирующих веществ, приведённых в таблице 5 (объёмы газообразных веществ даны при нормальных условиях);
б) расставьте коэффициенты в заданной схеме реакции и по уравнению реакции определите, какое из веществ находится в избытке, а какое в недостатке;
в) найдите химическое количество продукта реакции, указанного в таблице 5;
г) рассчитайте массу или объём (см. таблицу 5) этого продукта реакции.
Таблица 5 – Условия задания № 5
| № варианта | Реагирующие вещества | Схема реакции | Рассчитать |
| m(Fe)=11,2 г; V(Cl2)=5,376 л | Fe+Cl2 ® FeCl3 | m(FeCl3) | |
| m(Al)=5,4 г; m(H2SO4)=39,2 г | Al+H2SO4 ® Al2(SO4)3+H2 | V(H2) | |
| V(CO)=20 л; m(O2)=20 г | CO+O2 ® CO2 | V(CO2) | |
| m(AgNO3)=3,4 г; m(Na2S)=1,56 г | AgNO3+Na2S®Ag2S+NaNO3 | m(Ag2S) | |
| m(Na2CO3)=53 г; m(HCl)=29,2 г | Na2CO3+HCl®NaCl+CO2+H2O | V(CO2) | |
| m(Al2(SO4)3)=34,2 г;m(BaCl2)=52 г | Al2(SO4)3+BaCl2®AlCl3+BaSO4 | m(BaSO4) | |
| m(KI)=3,32 г; V(Cl2)=448 мл | KI+Cl2 ® KCl+I2 | m(I2) | |
| m(CaCl2)=22,2 г; m(AgNO3)=59,5 г | CaCl2+AgNO3®AgCl+Ca(NO3)2 | m(AgCl) | |
| m(H2)=0,48 г; V(O2)=2,8 л | H2+O2 ® H2O | m(H2O) | |
| m(Ba(OH)2)=3,42г; V(HCl)=784мл | Ba(OH)2+HCl ® BaCl2+H2O | m(BaCl2) |
Продолжение таблицы 5
| № варианта | Реагирующие вещества | Схема реакции | Рассчитать |
| m(H3PO4)=9,8 г; m(NaOH)=12,2 г | H3PO4+NaOH ® Na3PO4+H2O | m(Na3PO4) | |
| m(H2SO4)=9,8 г; m(KOH)=11,76 г | H2SO4+KOH ® K2SO4+H2O | m(K2SO4) | |
| V(Cl2)=2,24 л; m(KOH)=10,64 г | Cl2+KOH ® KClO+KCl+H2O | m(KClO) | |
| m((NH4)2SO4)=66 г;m(KOH)=50 г | (NH4)2SO4+KOH®K2SO4+NH3+H2O | V(NH3) | |
| m(NH3)=6,8 г; V(O2)=7,84 л | NH3+O2 ® N2+H2O | V(N2) | |
| V(H2S)=11,2 л; m(O2)=8,32 г | H2S+O2 ® S+H2O | m(S) | |
| m(MnO2)=8,7 г; m(HCl)=14,2 г | MnO2+HCl ® MnCl2+Cl2+H2O | V(Cl2) | |
| m(Al)=5,4 г; V(Cl2)=6,048 л | Al+Cl2 ® AlCl3 | m(AlCl3) | |
| m(Al)=10,8 г; m(HCl)=36,5 г | Al+HCl ® AlCl3+H2 | V(H2) | |
| m(P)=15,5 г; V(O2)=14,1 л | P+O2 ® P2O5 | m(P2O5) | |
| m(AgNO3)=8,5 г;m(K2CO3)=4,14 г | AgNO3+K2CO3®Ag2CO3+KNO3 | m(Ag2CO3) | |
| m(K2CO3)=69 г; m(HNO3)=50,4 г | K2CO3+HNO3®KNO3+CO2+H2O | V(CO2) | |
| m(AlCl3)=2,67 г; m(AgNO3)=8,5 г | AlCl3+AgNO3®AgCl+Al(NO3)3 | m(AgCl) | |
| m(KBr)=2,38 г; V(Cl2)=448 мл | KBr+Cl2 ® KCl+Br2 | m(Br2) | |
| m(CaBr2)=40 г; m(AgNO3)=59,5 г | CaBr2+AgNO3®AgBr+Ca(NO3)2 | m(AgBr) | |
| m(H2)=1,44 г; V(O2)=8,4 л | H2+O2 ® H2O | m(H2O) | |
| m(Ba(OH)2)=6,84 г;V(HI)=1,568 л | Ba(OH)2+HI ® BaI2+H2O | m(BaI2) | |
| m(H3PO4)=9,8 г; m(KOH)=17,08 г | H3PO4+KOH ® K3PO4+H2O | m(K3PO4) | |
| m(H2SO4)=49 г; m(NaOH)=45 г | H2SO4+NaOH ® Na2SO4+H2O | m(Na2SO4) | |
| V(Cl2)=2,24 л; m(KOH)=8,4 г | Cl2+KOH ® KClO3+KCl+H2O | m(KClO3) | |
| m(NH4Cl)=43 г; m(Ca(OH)2)=37 г | NH4Cl+Ca(OH)2®CaCl2+NH3+H2O | V(NH3) | |
| V(NH3)=8,96 л; m(O2)=14,4 г | NH3+O2 ® NO+H2O | V(NO) | |
| V(H2S)=17,92 л; m(O2)=40 г | H2S+O2 ® SO2+H2O | V(SO2) | |
| m(MnO2)=8,7 г; m(HBr)=30,8 г | MnO2+HBr ® MnBr2+Br2+H2O | m(MnBr2) | |
| m(Ca)=10 г; m(H2O)=8,1 г | Ca+H2O ® Ca(OH)2+H2 | V(H2) |
КОНЦЕНТРАЦИЯ РАСТВОРОВ
В рамках курса общей химии студенты изучают 2 способа выражения концентрации растворов – массовая доля и молярная концентрация.
Массовая доля растворённого вещества Х рассчитывается как отношение массы этого вещества к массе раствора:

где ω(X) – массовая доля растворённого вещества X;
m(X) – масса растворённого вещества X;
mраствора – масса раствора.
Массовая доля вещества, рассчитанная по приведённой выше формуле –безразмерная величина, выраженная в долях единицы (0 3 ) раствора
где C(X) – молярная концентрация растворённого вещества X (моль/л);
n(X) – химическое количество растворённого вещества Х (моль);
Vраствора – объём раствора (л).
Пример 5.1 Рассчитайте, молярную концентрацию H3PO4 в растворе, если известно, что массовая доля H3PO4 равна 60%, а плотность раствора – 1,43 г/мл.
По определению процентной концентрации
в 100 г раствора содержится 60 г фосфорной кислоты.
Vраствора = mраствора : ρраствора = 100 г : 1,43 г/см 3 = 69,93 см 3 = 0,0699 л;
Пример 5.2 Имеется 0,5 М раствор H2SO4. Чему равна массовая доля серной кислоты в этом растворе? Плотность раствора принять равной 1 г/мл.
По определению молярной концентрации
в 1 л раствора содержится 0,5 моль H2SO4
(запись «0,5 М раствор» означает, что С(H2SO4) = 0,5 моль/л).
mраствора = Vраствора × ρраствора = 1000 мл × 1 г/мл = 1000 г;
Пример 5.3 Какие объёмы воды и 96% раствора H2SO4 плотностью 1,84 г/мл необходимо взять для приготовления 2 л 60% раствора H2SO4 плотностью 1,5 г/мл.
При решении задач на приготовление разбавленного раствора из концентрированного следует учитывать, что исходный раствор (концентрированный), вода и полученный раствор (разбавленный) имеют различные плотности. В этом случае следует иметь в виду, что Vисходного раствора + Vводы ≠ Vполученного раствора ,
потому что в ходе смешивания концентрированного раствора и воды происходит изменение (увеличение или уменьшение) объёма всей системы.
Решение подобных задач нужно начинать с выяснения параметров разбавленного раствора (т.е. того раствора, который нужно приготовить): его массы, массы растворённого вещества, если необходимо, то и количества растворённого вещества.
Масса раствора, который необходимо приготовить, равна:
M60% р-ра = V60% р-ра ∙ ρ60% р-ра = 2000 мл × 1,5 г/мл = 3000 г.
Масса чистой серной кислоты в приготовленном растворе должна быть равна массе серной кислоты в той порции 96%-го раствора, которую необходимо взять для приготовления разбавленного раствора. Таким образом,
m (H2O) = m40% р-ра – m96% р-ра = 3000 г – 1875 г = 1125 г.
V96% р-ра = m96% р-ра : ρ96% р-ра = 1875 г : 1,84 г/мл = 1019 мл » 1,02 л.
Vводы = mводы : ρводы = 1125г : 1 г/мл = 1125 мл = 1,125 л.
Пример 5.4 Смешали 100 мл 0,1 M раствора CuCl2 и 150 мл 0,2 М раствора Cu(NO3)2 Рассчитать молярную концентрацию ионов Cu 2+ , Cl – и NO3 – в полученном растворе.
При решении подобной задачи на смешивание разбавленных растворов, важно понимать что разбавленные растворы имеют приблизительно одинаковую плотность, примерно равную плотности воды. При их смешивании общий объём системы практически не изменяется: V1 разбавленного раствора + V2 разбавленного раствора +…» Vполученного раствора.
В первом растворе:
n(CuCl2) = C(CuCl2) · Vраствора CuCl2 = 0,1 моль/л × 0,1 л = 0,01 моль;
CuCl2 – сильный электролит: CuCl2 ® Cu 2+ + 2Cl – ;
Поэтому n(Cu 2+ ) = n(CuCl2) = 0,01 моль; n(Cl – ) = 2 × 0,01 = 0,02 моль.
Во втором растворе:
Поэтому n(Cu 2+ ) = n(Cu(NO3)2) = 0,03 моль; n(NO3 – ) = 2×0,03 = 0,06 моль.
После смешивания растворов:
n(Cu 2+ )общ. = 0,01 моль + 0,03 моль = 0,04 моль;
Vобщ. » Vраствора CuCl2 + Vраствора Cu(NO3)2 = 0,1 л + 0,15 л = 0,25 л;
C(Cu 2+ ) = n(Cu 2+ ) : Vобщ. = 0,04 моль : 0,25 л = 0,16 моль/л;
C(Cl – ) = n(Cl – ) : Vобщ. = 0,02 моль : 0,25 л = 0,08 моль/л;
Пример 5.5 В колбу внесли 684 мг сульфата алюминия и 1 мл 9,8% раствора серной кислоты плотностью 1,1 г/мл. Образовавшуюся смесь растворили в воде; объём раствора довели водой до 500 мл. Рассчитать молярные концентрации ионов H + , Al 3+ SO4 2– в полученном растворе.
Рассчитаем количества растворяемых веществ:
Поэтому n(Al 3+ )=2×0,002 моль=0,004 моль; n(SO4 2– )=3×0,002 моль=0,006 моль.
m раствора H2SO4 = V раствора H2SO4 × ρ раствора H2SO4 = 1 мл × 1,1 г/мл = 1,1 г;
Поэтому n(SO4 2– ) = n(H2SO4) = 0,0011 моль; n(H + ) = 2 × 0,0011 = 0,0022 моль.
По условию задачи объём полученного раствора равен 500 мл (0,5 л).
n(SO4 2– )общ. = 0,006 моль + 0,0011 моль = 0,0071 моль.
С(Al 3+ ) = n(Al 3+ ) : Vраствора = 0,004 моль : 0,5 л = 0,008 моль/л;
С(H + ) = n(H + ) : Vраствора = 0,0022 моль : 0,5 л = 0,0044 моль/л;
С(SO4 2– ) = n(SO4 2– )общ. : Vраствора = 0,0071 моль : 0,5 л = 0,0142 моль/л.
Пример 5.6 Какую массу железного купороса (FeSO4·7H2O) и какой объём воды необходимо взять для приготовления 3 л 10% раствора сульфата железа (II). Плотность раствора принять равной 1,1 г/мл.
Масса раствора, который необходимо приготовить, равна:
mраствора = Vраствора ∙ ρраствора = 3000 мл ∙ 1,1 г/мл = 3300 г .
Масса чистого сульфата железа (II) в этом растворе равна:
m(FeSO4) = mраствора × w(FeSO4) = 3300 г × 0,1 = 330 г.
Такая же масса безводного FeSO4 должна содержаться в том количестве кристаллогидрата, которое необходимо взять для приготовления раствора. Из сопоставления молярных масс М(FeSO4·7H2O) = 278 г/моль и М(FeSO4) = 152 г/моль,
в 278 г FeSO4·7H2O содержится 152 г FeSO4;
в х г FeSO4·7H2O содержится 330 г FeSO4;
x = (278·330) : 152 = 603,6 г .
mводы = mраствора – mжелезного купороса = 3300 г – 603,6 г = 2696,4 г.
Т.к. плотность воды равна 1 г/мл, то объём воды, который необходимо взять для приготовления раствора равен: Vводы = mводы : ρводы = 2696,4 г : 1 г/мл = 2696,4 мл.
Пример 5.7 Какую массу глауберовой соли (Na2SO4·10H2O) нужно растворить в 500 мл 10% раствора сульфата натрия (плотность раствора 1,1 г/мл), чтобы получить 15%-ый раствор Na2SO4?
Пусть требуется x граммов глауберовой соли Na2SO4·10H2O. Тогда масса образующегося раствора равна:
m15% раствора = mисходного (10%) раствора + mглауберовой соли = 550 + x (г);
mисходного (10%) раствора = V10% раствора × ρ10% раствора = 500 мл × 1,1 г/мл = 550 г;
Выразим через икс массу чистого Na2SO4, содержащегося в х граммах Na2SO4·10H2O.
Общая масса сульфата натрия в полученном растворе будет равна:
В полученном растворе: 

Далее (таблица 6) приводится перечень задач для самостоятельного решения.
Задание №6
Таблица 6 – Условия задания № 6
| № варианта | Текст условия |
| В воде растворили 5 г Na2SO4×10H2O и объём образовавшегося раствора довели водой до 500 мл. Рассчитайте массовую долю Na2SO4 в этом растворе (ρ = 1 г/мл) и молярные концентрации ионов Na + и SO4 2– . | |
| Смешали растворы: 100 мл 0,05М Cr2(SO4)3 и 100 мл 0,02М Na2SO4. Рассчитайте молярные концентрации ионов Cr 3+ , Na + и SO4 2– в полученном растворе. | |
| Какие объёмы воды и 98%-ного раствора (плотность 1,84 г/мл) серной кислоты нужно взять для приготовления 2 литров 30%-го раствора, плотностью 1,2 г/мл? | |
| В 400 мл воды растворили 50 г Na2CO3×10H2O. Каковы молярные концентрации ионов Na + и CO3 2– и массовая доля Na2CO3 в полученном растворе (ρ=1,1 г/мл)? | |
| Смешали растворы: 150 мл 0,05 М Al2(SO4)3 и 100 мл 0,01 М NiSO4. Рассчитайте молярные концентрации ионов Al 3+ , Ni 2+ , SO4 2- в полученном растворе. | |
| Какие объёмы воды и 60%-го раствора (плотность 1,4 г/мл) азотной кислоты потребуются для приготовления 500 мл 4 М раствора (плотностью 1,1 г/мл)? | |
| Какая масса медного купороса (CuSO4×5H2O) необходима для приготовления 500 мл 5% раствора сульфата меди плотностью 1,05 г/мл? | |
| В колбу внесли 1 мл 36%-ного раствора (ρ = 1,2 г/мл) HCl и 10 мл 0,5 М раствора ZnCl2. Объём образовавшегося раствора довели водой до 50 мл. Каковы молярные концентрации ионов H + , Zn 2+ , Cl – в полученном растворе? | |
| Какова массовая доля Cr2(SO4)3 в растворе (ρ » 1 г/мл), если известно, что молярная концентрация сульфат ионов в этом растворе равна 0,06 моль/л? | |
| Какие объёмы воды и 10 М раствора (ρ=1,45 г/мл) гидроксида натрия потребуются для приготовления 2 л 10% раствора NaOH (ρ= 1,1 г/мл)? | |
| Сколько граммов железного купороса FeSO4×7H2O можно получить, выпарив воду из 10 л 10%-го раствора сульфата железа (II) (плотность раствора 1,2 г/мл)? | |
| Смешали растворы: 100 мл 0,1 М Cr2(SO4)3 и 50 мл 0,2 М CuSO4. Рассчитать молярные концентрации ионов Cr 3+ , Сu 2+ , SO4 2- в полученном растворе. |
Продолжение таблицы 6
| № варианта | Текст условия |
| Какие объёмы воды и 40%-го раствора фосфорной кислоты с плотностью 1,35 г/мл потребуются для приготовления 1 м 3 5%-го раствора H3PO4, плотность которого равна 1,05 г/мл? | |
| В воде растворили 16,1 г Na2SO4×10H2O и объём образовавшегося раствора довели водой до 250 мл. Рассчитайте массовую долю и молярную концентрацию Na2SO4 в образовавшемся растворе (плотность раствора считать равной 1 г/мл). | |
| Смешали растворы: 150 мл 0,05 М Fe2(SO4)3 и 100 мл 0,1 М MgSO4. Рассчитайте молярные концентрации ионов Fe 3+ , Mg 2+ , SO4 2– в полученном растворе. | |
| Какие объёмы воды и 36% соляной кислоты (плотностью 1,2 г/мл) необходимы для приготовления 500 мл 10%-го раствора, плотность которого 1,05 г/мл? | |
| В 200 мл воды растворили 20 г Al2(SO4)3×18H2O. Какова массовая доля растворённого вещества в полученном растворе, плотность которого равна 1,1 г/мл? Рассчитайте молярные концентрации ионов Al 3+ и SO4 2– в этом растворе. | |
| Смешали растворы: 100 мл 0,05 М Al2(SO4)3 и 150 мл 0,01 М Fe2(SO4)3. Рассчитайте молярные концентрации ионов Fe 3+ , Al 3+ и SO4 2– в полученном растворе. | |
| Какие объёмы воды и 80% раствора уксусной кислоты (плотностью 1,07 г/мл) потребуются для приготовления 0,5 л столового уксуса, в котором массовая доля кислоты составляет 7%? Плотность столового уксуса принять равной 1 г/мл. | |
| Какая масса железного купороса (FeSO4×7H2O) необходима для приготовления 100 мл 3% раствора сульфата железа? Плотность раствора равна 1 г/мл. | |
| В колбу внесли 2 мл 36% раствора HCl (плотность 1,2 г/см 3 ) и 20 мл 0,3 М раствора CuCl2. Объём образовавшегося раствора довели водой до 200 мл. Рассчитайте молярные концентрации ионов H + , Cu 2+ и Cl – в полученном растворе. | |
| Чему равна процентная концентрация Al2(SO4)3 в растворе, в котором молярная концентрация сульфат-ионов равна 0,6 моль/л. Плотность раствора 1,05 г/мл. | |
| Какие объёмы воды и 10 М раствора KOH (плотность раствора 1,4 г/мл) потребуются для приготовления 500 мл 10% раствора KOH плотностью 1,1 г/мл? | |
| Сколько граммов медного купороса CuSO4×5H2O можно получить, выпарив воду из 15 л 8% раствора сульфата меди, плотность которого равна 1,1 г/мл? | |
| Смешали растворы: 200 мл 0,025 М Fe2(SO4)3 и 50 мл 0,05 М FeCl3. Рассчитайте молярные концентрацию ионов Fe 3+ , Cl – , SO4 2– в полученном растворе. | |
| Какие объёмы воды и 70% раствора H3PO4 (плотностью 1,6 г/мл) потребуются для приготовления 0,25 м 3 10%-го раствора H3PO4 (плотностью 1,1 г/мл)? | |
| В 100 мл воды растворили 6 г Al2(SO4)3×18H2O. Рассчитайте массовую долю Al2(SO4)3 и молярные концентрации ионов Al 3+ и SO4 2– в полученном растворе, плотность которого равна 1 г/мл. | |
| Смешали растворы: 50 мл 0,1 М Cr2(SO4)3 и 200 мл 0,02 М Cr(NO3)3. Рассчитайте молярные концентрации ионов Cr 3+ , NO3 – , SO4 2- в полученном растворе. | |
| Какие объёмы 50% раствора хлорной кислоты (плотность 1,4 г/мл) и воды необходимы для приготовления 1 литра 8%-го раствора плотностью 1,05 г/мл? | |
| Сколько граммов глауберовой соли Na2SO4×10H2O нужно растворить в 200 мл воды, чтобы получить 5%-ый раствор сульфата натрия? | |
| В колбу внесли 1 мл 80% раствора H2SO4 (плотность раствора 1,7 г/мл) и 5000 мг Cr2(SO4)3. Смесь растворили в воде; объём раствора довели до 250 мл. Рассчитайте молярные концентрации ионов H + , Cr 3+ и SO4 2– в полученном растворе. |
Продолжение таблицы 6
| № варианта | Текст условия |
| Какие объёмы воды и 14 М раствора гидроксида калия (плотность 1,5 г/мл) потребуются для приготовления 500 мл 10% раствора KOH (плотность 1,12 г/мл)? | |
| Рассчитайте молярные концентрации ионов Al 3+ и SO4 2– в 17,1% растворе сульфата алюминия. Плотность раствора принять равной 1,1 г/см 3 . | |
| Сколько граммов кристаллогидрата CaCl2×6H2O нужно добавить к 200 мл 5% раствора хлорида кальция плотностью 1 г/мл, чтобы получить 20% раствор CaCl2? | |
| Какие объёмы воды и 90% раствора фосфорной кислоты (плотность 1,75 г/мл) потребуются для приготовления 500 мл 30% раствора плотностью 1,2 г/мл? |
ХИМИЧЕСКОЕ РАВНОВЕСИЕ
Все химические реакции можно разделить на 2 группы: реакции необратимые, т.е. протекающие до полного израсходования хотя бы одного из реагирующих веществ, и реакции обратимые, в которых ни одно из реагирующих веществ не расходуется полностью. Это связано с тем, что обратимая реакция может протекать как в прямом, так и в обратном направлении. Классическим примером обратимой реакции может служить реакция синтеза аммиака из азота и водорода:
В момент начала реакции концентрации исходных веществ в системе максимальны; в этот момент максимальна и скорость прямой реакции. В момент начала реакции в системе ещё отсутствуют продукты реакции (в данном примере – аммиак), следовательно, скорость обратной реакции равна нулю. По мере взаимодействия исходных веществ друг с другом, их концентрации уменьшаются, следовательно, уменьшается и скорость прямой реакции. Концентрация же продукта реакции постепенно возрастает, следовательно, возрастает и скорость обратной реакции. Через некоторое время скорость прямой реакции становится равна скорости обратной. Это состояние системы называется состоянием химического равновесия. Концентрации веществ в системе, находящейся в состоянии химического равновесия, называются равновесными концентрациями. Количественной характеристикой системы в состоянии химического равновесия является константа равновесия.

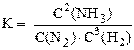
Следует иметь в виду, что в выражение константы равновесия входят равновесные концентрации только газообразных веществ или веществ, находящихся в растворённом состоянии. Концентрация твёрдого вещества считается постоянной и не записывается в выражение константы равновесия.

Существует два наиболее важных типа задач, связанных с расчётом параметров равновесной системы:
1) известны начальные концентрации исходных веществ; из условия задачи можно найти концентрации веществ, прореагировавших (или образовавшихся) к моменту наступления равновесия; в задаче требуется рассчитать равновесные концентрации всех веществ и численную величину константы равновесия;
2) известны начальные концентрации исходных веществ и константа равновесия. В условии нет данных о концентрациях прореагировавших или образовавшихся веществ. Требуется рассчитать равновесные концентрации всех участников реакции.
Для решения подобных задач необходимо понимать, что равновесную концентрацию любого исходного вещества можно найти, отняв от начальной концентрации концентрацию прореагировавшего вещества:
С равновесная = С начальная – С прореагировавшего вещества .
Равновесная концентрация продукта реакции равна концентрации продукта, образовавшегося к моменту наступления равновесия:
С равновесная = С образовавшегося продукта .
Таким образом, для расчёта параметров равновесной системы очень важно уметь определить, сколько к моменту наступления равновесия прореагировало исходного вещества и сколько образовалось продукта реакции. Для определения количества (или концентрации) прореагировавшего и образовавшегося веществ проводятся стехиометрические расчёты по уравнению реакции.
Пример 6.1 Начальные концентрации азота и водорода в равновесной системе N2 + 3H2 ⇆ 2 NH3 соответственно равны 3 моль/л и 4 моль/л. К моменту наступления химического равновесия в системе осталось 70% водорода от его первоначального количества. Определить константу равновесия данной реакции.
Для того чтобы рассчитать константу равновесия, необходимо сначала рассчитать равновесные концентрации всех участников реакции и затем подставить их в выражение константы равновесия.
Из условия задачи следует, что к моменту наступления равновесия прореагировало 30% водорода (задача 1 типа):
Как видно из уравнения реакции, азота должно было вступить в реакцию в 3 раза меньше, чем водорода, т.е. С прореаг.(N2) = 1,2 моль/л : 3 = 0,4 моль/л. Аммиака же образуется в 2 раза больше, чем прореагировало азота:
Собразов.(NH3) = 2 × 0,4 моль/л = 0,8 моль/л
Равновесные концентрации всех участников реакции будут таковы:


Пример 6.2 Рассчитать равновесные концентрации водорода, йода и йодоводорода в системе H2 + I2 ⇆ 2 HI, если известно, что начальные концентрации H2 и I2 равны 5 моль/л и 3 моль/л соответственно, а константа равновесия равна 1.
Следует обратить внимание, что в условии этой задачи (задача 2 типа) в условии ничего не говорится о концентрациях прореагировавших исходных веществ и образовавшихся продуктов. Поэтому при решении таких задач обычно концентрация какого-нибудь прореагировавшего вещества принимается за икс.
Пусть к моменту наступления равновесия прореагировало x моль/л H2. Тогда, как следует из уравнения реакции, должно прореагировать x моль/л I2, и образоваться 2x моль/л HI. Равновесные концентрации всех участников реакции будут таковы:
Далее необходимо подставить выраженные через икс равновесные концентрации в формулу для константы равновесия и решить полученное уравнение.
4x 2 = 15 – 8x + x 2
3x 2 + 8x – 15 = 0
Физический смысл имеет только положительный корень x = 1,27.
Следовательно, Сравн.(H2) = (5 – x) моль/л = 5 – 1,27 = 3,73 моль/л;
Сравн.(I2) = (3 – x) моль/л = 3 – 1,27 = 1,73 моль/л;
Сравн.(HI) = 2x моль/л = 2·1,27 = 2,54 моль/л.
Далее (таблица 7) приводятся условия задач по теме «Химическое равновесие» для самостоятельного решения.
- Стехиометрические расчёты
- Стехиометрические расчёты
- Решение задач по уравнениям химических реакций
- Закон авогадро и молярный объем газов
- Доказательство закона Авогадро
- Определение плотности газов
- Нахождение объема, числа молекул, количества вещества по известной массе газа и обратные задачи
- Относительная плотность газов
- Нахождение относительной плотности
- Расчет молярных масс газов по относительным плотностям газов
- Расчет массы неизвестного газа по значению относительной плотности
- Закон объемных отношений
- Образование
- Сумма коэффициентов в уравнении окислительно восстановительной реакции
- Сумма коэффициентов в уравнении окислительно восстановительной реакции
- Оставить ответ Отменить ответ
- 🔍 Видео
Видео:Расстановка Коэффициентов в Химических Реакциях // Подготовка к ЕГЭ по ХимииСкачать

Стехиометрические расчёты
Содержание:
Одним из важнейших химических понятий, на котором основываются стехиометрические расчёты, является химическое количество вещества. Количество некоторого вещества X обозначается n(X). Единицей измерения количества вещества является моль.
Моль – это количество вещества, в котором содержится 6,02·10 23 молекул, атомов, ионов или других структурных единиц, из которых состоит вещество.
На странице -> решение задач по химии собраны решения задач и заданий с решёнными примерами по всем темам химии.
Видео:Расстановка коэффициентов в химических реакциях: как просто это сделатьСкачать

Стехиометрические расчёты
Стехиометрическими расчетами называют нахождение значений количества, масс и объемов веществ (реагентов и продуктов), участвующих в химических реакциях. Формульное количество вещества B (nB) и масса этого вещества (mB) связаны между собой соотношением.
Решение задач по уравнениям химических реакций
Вспомните! Уравнения химических реакций. Закон сохранения массы вещества. Составление и решение пропорции
По уравнениям химических реакций можно решать множество количественных задач. Мы остановимся на расчетных задачах по нахождению массы (m) и числа молей 
Решение задач осуществляется по следующему алгоритму:







Задача 1. Сколько граммов хлорида натрия образуется при взаимодействии 92 г натрия с хлором?

Задача 2. Сколько молей углекислого газа образуется при горении 36 г углерода?

Задача 3. Вычислите массу цинка (Zn), который должен взаимодействовать с соляной кислотой с выделением 10 г водорода.

Задача 4. Рассчитайте количество веществ оксида меди (CuO) и углекислого газа, полученных при разложении 5 г малахита 


а) 1 моль (м-т) : 2 моля (CuO) = 0,0225 моль (м-т) : х моль (CuO)
х = 0,045 моль (CuO)

0,0225 моль 
Закон авогадро и молярный объем газов
Какие газы вы знаете? Что такое плотность?
Многие химические вещества существуют в газообразном состоянии, например 




Объем газов зависит от температуры и давления. При постоянном давлении и температуре расстояния между молекулами газообразных веществ примерно одинаковы.
Из курса физики вам известно понятие «плотность»

В таблице 8 приведены некоторые величины, характеризующие известные вам газы.
Рассчитаем объем 1 моля каждого газа (при н.у.):
Как видно из этих расчетов, объемы одного моля различных газов при нормальных условиях (н. у.), т. е. при температуре 0°С и давлении 1 атм (101,3 кПа), примерно одинаковы и составляют 22,4 л. При стандартных условиях (t = 25°С, p = 101,3 кПа) молярный объем составляет 24 л. Эта величина называется молярным объемом и обозначается 

количеству вещества
В 1 моль любых веществ, в том числе и газах, содержится одинаковое число молекул, которое называется числом Авогадро 
В равных объемах газов, взятых при одинаковых условиях, содержится одинаковое число молекул. Этот закон был сформулирован итальянским ученым Авогадро в 1811 году.
Плотностью газа при н. у. называется отношение молярной массы газа на молярный объем.
Плотность газа при нормальных условиях:
Доказательство закона Авогадро
Найдите число молекул и массы кислорода и углекислого газа объемом 50 л, взятых при нормальных условиях (н. у.).
Число молекул равных объемов (50 л) газов, взятых при одинаковых условиях (н. у.), одинаково.
Расчет масс газов.
Массы газов разные.
Определение плотности газов
Найдите плотности кислорода и углекислого газа при нормальных условиях.
Нахождение объема, числа молекул, количества вещества по известной массе газа и обратные задачи
а) Определите объем, число молекул, количество вещества 8,8 г углекислого газа при н. у.
б) Рассчитайте массу, количество вещества и число молекул 67,2 л кислорода при н. у.
в) Рассчитать объем, массу, число молекул в 0,5 моль аммиака (н. у.).
г) Определите объем (н. у), массу и количество вещества сернистого газа числом молекул
Нормальные и стандартные условия, молярный объем, число и закон Авогадро.
Относительная плотность газов
Кроме плотности веществ, в химии часто применяют понятие относительная плотность.
Относительной плотностью (D) одного газа по отношению к другому газу называется отношение масс газов, взятых в равных объемах при одинаковых условиях.
Часто относительную плотность различных газов определяют по отношению к водороду или воздуху.
По формулам относительных плотностей можно рассчитать значение молярной массы газов.
Нахождение относительной плотности
Рассчитайте относительные плотности кислорода и углекислого газа по водороду и воздуху
Расчет молярных масс газов по относительным плотностям газов
Рассчитать молярные массы газов, если известны относительные плотности:
Расчет массы неизвестного газа по значению относительной плотности
Рассчитайте массу 50 л (н. у.) неизвестного газа, если относительная плотность этого газа по воздуху равна 0,586. Какова относительная плотность по водороду?
Закон объемных отношений
Напишем уравнение реакции между газообразными веществами, когда в результате реакции также образуется газ:
Отношение количеств реагирующих и образовавшихся веществ выглядит следующим образом: 2 : 1 : 2. Теперь возьмем отношение объемов этих газов при нормальных условиях:
Как видим, отношения объемов газов соответствуют отношениям коэффициентов перед формулами веществ в уравнении.
При одинаковых условиях объемы реагирующих газов и газообразных продуктов реакции относятся между собой как небольшие целые числа. Это закон объемных отношений Гей-Люссака.
Из рассмотренных примеров можно сделать вывод, что при решении задач удобно пользоваться коэффициентами, т.к. они в уравнениях химических реакций указывают объемные отношения веществ.
Определите объем кислорода, необходимого для окисления 60 л оксида серы (IV) до оксида серы (VI) по уравнению:
Закон объемных отношений.
- 1. Моль — мера количества вещества. В 1 моль любого вещества содержится число Авогадро структурных единиц (6,02-1023).
- 2. Молярная масса вещества (М) численно равна относительной молекулярной массе (Мг).
- 3. Расчеты по химическим уравнениям производятся на основе закона сохранения масс веществ.
- 4. В равных объемах газов, взятых при одинаковых условиях, содержится одинаковое число молекул. (Закон Авогадро.)
- 5. Относительной плотностью одного газа по отношению к другому газу (Dy(X)) называется отношение масс газов, взятых в равных объемах при одинаковых условиях.
- 6. Объемы реагирующих газообразных веществ относятся между собой и к объемам образующихся газообразных продуктов, как небольшие целые числа, равные коэффициентам в уравнении химической реакции. (Закон объемных отношений Гей-Люссака.)
- 7. При нормальных условиях (н. у.) любой газ занимает 22,4 л. Эта величина называется молярным объемом (У = 22,4 л/моль).
Услуги по химии:
Лекции по химии:
Лекции по неорганической химии:
Лекции по органической химии:
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Видео:Как расставлять коэффициенты в уравнении реакции? Химия с нуля 7-8 класс | TutorOnlineСкачать

Образование
Помощь в обучении
Видео:8 класс. Химия. Как расставить коэффициенты в уравнении?Скачать

Сумма коэффициентов в уравнении окислительно восстановительной реакции
Видео:Расстановка коэффициентов в химических реакциях: как просто это сделатьСкачать
Сумма коэффициентов в уравнении окислительно восстановительной реакции
Сумма,или подбор стехиометрических коэффициентов при написании уравнений окислительно-восстановительных реакций основан на равенстве числа электронов,отдаваемых восстановителем и получаемых окислителем.
Искомая сумма вычисляется в несколько этапов.Рассмотрим на примере реакции лабораторного получения хлора окислением хлороводорода HCl перманганатом калия KMnO4,который при этом восстанавливается до иона Mn+2.
1.Уравнения полуреакций в явном виде(при участии молекул воды):
MnO4[-] + 8H[+] + 5e -> Mn[+2] + 4H2O
2.Необходимо уравнять число электронов в обеих полуреакциях,Первое уравнение надо умножить на 2,второе на 5:
2MnO4[-] + 16H[+] + 10e -> 2Mn[+2] + 8H2O
3.Суммируем уравнения и получаем уравнение в ионном виде:
2MnO4[-] + 16H[+] + 10Cl[-] -> 2Mn[+2] + 8H2O + 5Cl2[0]
В конечном уравнении правая часть должна быть равна левой,включая сумму зарядов ионов(в нашем случае +4,так как 16−10−2=2×2).
Оставить ответ Отменить ответ
Этот сайт использует Akismet для борьбы со спамом. Узнайте, как обрабатываются ваши данные комментариев.
🔍 Видео
Расстановка коэффициентов в окислительно-восстановительных реакцияхСкачать

СУММА КОЭФФИЦИЕНТОВ: Как решать Квадратные Уравнения по МАТЕМАТИКЕ 8 классСкачать

89. Как расставить коэффициенты реакции методом электронного баланса (закрепление)Скачать

В окислительно-восстановительной реакции найдите сумму коэффициентов в правой части уравнения.Скачать

Химические уравнения // Как Составлять Уравнения Реакций // Химия 9 классСкачать

Что такое знак СУММЫ и как он работает?Скачать

Составление уравнений химических реакций. 1 часть. 8 класс.Скачать

Химические уравнения 8 класс - как расставить коэффициенты ?Скачать

Стехиометрический расчётСкачать

Расчеты по уравнениям химических реакций. 1 часть. 8 класс.Скачать

Как вычислить коэффициент асимметрии и коэффициент эксцесса?Скачать

Как Решать Задачи по Химии // Задачи с Уравнением Химической Реакции // Подготовка к ЕГЭ по ХимииСкачать

Порядок реакцииСкачать

Стехиометрические расчеты. Практическая часть - решение задачи. 9 класс.Скачать

Химические уравнения. СЕКРЕТНЫЙ СПОСОБ: Как составлять химические уравнения? Химия 8 классСкачать
























































