Как определить, принадлежит ли графику функции точка? Это можно сделать, не выполняя построения графика.
График функции проходит через точку, если координаты этой точки обращают формулу функции в верное числовое равенство.
Таким образом, чтобы выяснить, принадлежит ли графику функции точка, надо подставить координаты точки в формулу функции. Если получится верное числовое равенство, точка лежит на графике.
1) Принадлежат ли графику функции y=10x-3 точки A(-2; 17) и B(1; 7)?
График функции проходит через точки A и B, если их координаты обращают формулу y=10x-3 в верное числовое равенство.
Подставляем в формулу функции вместо y ординату точки A (y=17), а вместо x — абсциссу (x=-2). Имеем:
Значит, точка A графику функции y=10x-3 не принадлежит.
Ординату 7 точки B подставляем в формулу функции y=10x-3 вместо y, абсциссу 1 — вместо x. Имеем:
Следовательно, точка B принадлежит графику функции y=10x-3.
Ответ: точка B принадлежит графику функции, точка A — не принадлежит.
2) Какие из точек A(2;15), B(-1;-15), C(-10; 243) принадлежат графику функции y=3x²+5x-7?
В формулу функции y=3x²+5x-7 вместо y подставляем ординату точки, вместо каждого x — абсциссу.
Верные равенства получили для точек A и C. Значит, эти точки принадлежат графику функции y=3x²+5x-7, а точка B — не принадлежит.
Ответ: точки A и C принадлежат графику функции.
Видео:8 класс. График функции. Принадлежит ли точка графику функции. Как узнать?Скачать

Построение графиков функций
О чем эта статья:
11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Видео:Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

Понятие функции
Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
- Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
- Графический способ — наглядно.
- Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
- Словесный способ.
Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.
Например, для функции вида 
- х ≠ 0, потому что на ноль делить нельзя. Записать можно так: D (y): х ≠ 0.
Область значений — множество у, то есть это значения, которые может принимать функция.
Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.
Видео:Определить, принадлежит ли точка с заданными координатами графику функцииСкачать

Понятие графика функции
Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.
График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.
Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.
Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.
В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.
Отметим любые три точки на координатной плоскости, например: L (-2; -2), M (0; 0) и N (1; 1).
Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:
Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.
Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.
Видео:Принадлежит ли точка графику функции. Алгебра 7 классСкачать

Исследование функции
Важные точки графика функции y = f(x):
- стационарные и критические точки;
- точки экстремума;
- нули функции;
- точки разрыва функции.
Стационарные точки — точки, в которых производная функции f(x) равна нулю.
Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.
Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.
Нули функции — это значения аргумента, при которых функция равна нулю.
Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.
Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:
Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.
Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.
Схема построения графика функции:
- Найти область определения функции.
- Найти область допустимых значений функции.
- Проверить не является ли функция четной или нечетной.
- Проверить не является ли функция периодической.
- Найти нули функции.
- Найти промежутки знакопостоянства функции, то есть промежутки, на которых она строго положительна или строго отрицательна.
- Найти асимптоты графика функции.
- Найти производную функции.
- Найти критические точки в промежутках возрастания и убывания функции.
- На основании проведенного исследования построить график функции.
| x | y |
| 0 | -1 |
| 1 | 2 |
Как видим, k = 3 > 0 и угол наклона к оси Ox острый, b = -1 — смещение по оси Oy.
| x | y |
| 0 | 2 |
| 1 | 1 |
k = -1 > 0 и b = 2 можно сделать аналогичные выводы, как и в первом пункте.
| x | y |
| 0 | 0 |
| 1 | 2 |
k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.
k = 0 — константная функция, прямая проходит через точку b = -1 и параллельно оси Ox.
Задача 5. Построить график функции
Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.
Нули функции: 3, 2, 6.
Промежутки знакопостоянства функции определим с помощью метода интервалов.
Вертикальные асимптоты: x = 0, x = 4.
Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.
Вот так выглядит график:
Задача 6. Построить графики функций:
б)
г)
д)
Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.
а)
Преобразование в одно действие типа f(x) + a.
Сдвигаем график вверх на 1:
б)
Преобразование в одно действие типа f(x — a).
Сдвигаем график вправо на 1:
В этом примере два преобразования, выполним их в порядке действий: сначала действия в скобках f(x — a), затем сложение f(x) + a.
Сдвигаем график вправо на 1:
Сдвигаем график вверх на 2:
г)
Преобразование в одно действие типа
Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:
д)
Мы видим три преобразования вида f(ax), f (x + a), -f(x).
Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.


Сжимаем график в два раза вдоль оси абсцисс:

Сдвигаем график влево на 1/2 вдоль оси абсцисс:

Отражаем график симметрично относительно оси абсцисс:
Видео:7 кл.Принадлежит ли графику функции 3x+4y=12 точка А(4;1)Скачать

Принадлежат ли графику Алгебра Макарычев Ю.Н. 7 класс 303
Помогите пожайлуста ответить на вопрос:
Принадлежат ли графику функции у = -0,5х точки А(0; 1), В(-1; 0,5), С(2; -1), D(4; -2)?
Решение задачи, следует таким образом:
Чтобы проверить, принадлежит точка графику функции или нет, необходимо в уравнение функции подставить координаты данной точки, если получится верное равенство, то точка принадлежит графику у = -0,5х.
A (0; 1); -0,5х = -0,5* 1 == -0‚5; 0 ≠ -0‚5 — точка А не принадлежит.
В (-1;0‚5); -0,5х = -0‚5 *(-1) = 0,5; 0,5 = 0,5 — точка В принадлежит.
С (2;-1); -0,5х = -0,5 * 2 = -1; -1 = -1- точка С принадлежит.
D (4; -2); -0,5х = -0‚5 — 4 = -2; -2 : -2 — точка D принадлежит.
🔥 Видео
Определим,проходит ли график через данную точку.Скачать

Построить график ЛИНЕЙНОЙ функции и найти:Скачать

Как построить график линейной функции.Скачать

Определение графика линейной функции по его формулеСкачать

Алгебра 7 класс. Как определить лежит ли точка с заданными координатами на графике функции (3 из 5).Скачать

Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать

Попадание точки в заданную область. Два сектора. Уроки программирования на С++.Скачать

Функция у=х² и у=х³ и их графики. Алгебра, 7 классСкачать

Вариант 72, № 2. Выбрать точку, принадлежащую графику уравнения ax+by=cСкачать

Как запомнить графики функцийСкачать

Линейная функция и её график. Алгебра, 7 классСкачать

Как построить график функции без таблицыСкачать

10 класс, 43 урок, Уравнение касательной к графику функцииСкачать

ГРАФИК ФУНКЦИИ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать
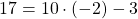
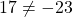
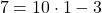
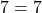
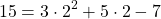
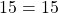
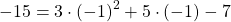
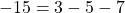
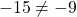
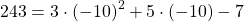
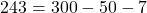
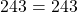







 при х ≠ -1.
при х ≠ -1.






 , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.
, т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0. , т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b
, т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b























