Как получить характеристическое уравнение из передаточной функции разомкнутой системы (2 видео)

Содержание

Вывод характеристического уравнения замкнутой системы из передаточных функций объекта и регулятора
Связь передаточных функций и частотных характеристик разомкнутого и замкнутого контуров системы автоматического управления
Типовые передаточные функции и характеристическое уравнение
🔥 Видео

Видео:ТАУ. Matlab/Simulink - моделирование передаточной функции, снятие характеристикСкачать

Вывод характеристического уравнения замкнутой системы из передаточных функций объекта и регулятора

Для исследования замкнутой системы на устойчивость необходимо знать математические модели — передаточные функции всех элементов САУ. Для укрупненной структурной схемы САУ — это передаточные функции объекта и регулятора. Выясним, как, используя передаточные функции объекта и регулятора, определить характеристическое уравнение замкнутой системы, через корни которого можно оценить устойчивость проектируемой САУ. Это можно сделать двумя способами.

Первый способ. Запишем передаточную функцию замкнутой САУ через передаточные функции объекта и регулятора с параллельно-встречным соединением звеньев с отрицательной ОС (см. рис. 5.6 и 6.1, в):

Используем передаточные функции объекта и регулятора, полученные при выводе характеристического уравнения замкнутой САУ (см. рис. 7.3):

Если после проведенных алгебраических преобразований знаменатель передаточной функции замкнутой САУ приравнять нулю, получим характеристическое уравнение замкнутой системы. Следует отметить, что последнее выражение есть передаточная функция замкнутой системы с возмущающим воздействием X, (см. рис. 6.2) со стороны регулирующего органа. В общем виде она будет иметь вид

Запишем в общем виде передаточную функцию замкнутой системы с возмущающим воздействием Х₃ (см. рис. 6.2) со стороны задатчика:

Сравнив знаменатели И ) и И^ 3 _мСАУ (/>), можно сделать вывод, что характеристические уравнения замкнутых САУ с возмущающим воздействием X, со стороны регулирующего органа и возмущающим воздействием Х₃ со стороны задатчика будут одинаковыми.

Недостаток рассмотренного способа вывода характеристического уравнения замкнутой САУ состоит в том, что при алгебраических преобразованиях четырехэтажной дроби передаточной функции легко ошибиться и, следовательно, получить с ошибками после преобразований знаменатель обычной дроби. Этого недостатка лишен другой способ.

Второй способ. С помощью передаточных функций объекта и регулятора запишем передаточную функцию выбранной разомкнутой системы:

Затем суммируем знаменатель и числитель полученной обычной дроби и эту сумму приравниваем к нулю. В результате запишем характеристическое уравнение замкнутой системы:

или

Запишем передаточную функцию замкнутой САУ в общем виде:

Выражение B(p)D(p) + А(р)С(р) = 0 и есть характеристическое уравнение замкнутой САУ.

Однако после получения характеристического уравнения замкнутой САУ возникают новые трудности. Дело в том, что современная математика не позволяет решать в общем виде алгебраические уравнения (а характеристические уравнения замкнутой САУ — это алгебраические уравнения) выше 3-го порядка (в которых неизвестное р в третьей степени), тогда как для реальных промышленных систем, состоящих из множества элементов (см. рис. 6.1), часто требуется решение уравнений 4-го, 6-го и выше порядков. Поэтому в ТАУ разработаны косвенные методы (ТАУ является практичной инженерной теорией), позволяющие определить знаки всех корней характеристического уравнения замкнутой САУ без решения самого уравнения. Эти методы назвали критериями устойчивости.

Видео:proТАУ: 1. Передаточная функцияСкачать

Связь передаточных функций и частотных характеристик разомкнутого и замкнутого контуров системы автоматического управления

Передаточные функции находят широкое применение при исследовании систем автоматического управления. Зная передаточную функцию, можно определить временные и частотные характеристики системы. Кроме того, можно определить и изменение регулируемой величины при приложении к системе воздействий произвольной формы.

В зависимости от того, рассматривается ли поведение системы при задающем или при возмущающем воздействии, различают передаточные функции системы по задающему и по возмущающему воздействиям. При этом различают передаточные функции разомкнутых и замкнутых систем.

Рассмотрим понятие передаточной функции системы по задающему воздействию.

Передаточной функцией системы по задающему воздействию называется отношение изображения по Лапласу выходной величины системы X(p)=L[x(t)] к изображению по Лапласу задающего воздействия G(p)=L[g(t)] при нулевых начальных условиях.

Передаточная функция замкнутой системы по задающему воздействию обозначается через Ф(р) и равна

. (7.10)

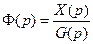
Передаточная функция разомкнутой системы по задающему воздействию обозначается через W(p) и равна

, (7.11)

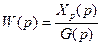
где X_р(p) – изображение по Лапласу выходной величины разомкнутой системы при нулевых начальных условиях.

Передаточной функцией системы по возмущающему воздействию называется отношение изображения по Лапласу выходной величины системы к изображению по Лапласу возмущающего воздействия F(p)=L[f(t)] при нулевых начальных условиях.

Передаточная функция замкнутой системы по возмущающему воздействию обозначается через F_f(p) и равна

. (7.12)

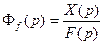
Передаточная функция разомкнутой системы по возмущающему воздействию обозначается через V(p) и равна

. (7.13)

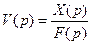
При определении передаточных функций разомкнутых систем имеется в виду, что рассматривается поведение системы, у которой главная отрицательная обратная связь разомкнута.

Кроме рассмотренных выше передаточных функций, при анализе систем автоматического регулирования очень часто используют передаточную функцию замкнутой системы по ошибке.

Передаточной функцией замкнутой системы по сигналу ошибки называется отношение изображения по Лапласу ошибки к изображению по Лапласу задающего воздействия при нулевых начальных условиях. Она равна

, (7.14)

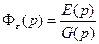
где E(p)=L[e(t)] – изображение по Лапласу ошибки системы при нулевых начальных условиях.

Определим связь между передаточными функциями разомкнутой и замкнутой систем автоматического регулирования. Так как структурная схема любой сложной многоконтурной системы с одной регулируемой величиной методами структурных преобразований может быть приведена к схеме одноконтурной системы, то в общем случае структурная схема САУ может быть представлена так, как изображено на рис.7.5,а. Задающее воздействие g(t) приложено ко входу звена с передаточной функцией W₁(p), а возмущающее воздействие f(t) действует на вход звена W₂(p). Разомкнем систему, т.е. отключим выход звена W₂(p) от сумматора. Структурная схема примет вид, изображенный на рис.7.5,б.

Пользуясь правилом структурных преобразований и применяя принцип суперпозиции, так как САУ является линейной, определим передаточные функции разомкнутой системы.

Передаточная функция разомкнутой системы по задающему воздействию при f(t)=0 будет равна

, (7.15)

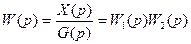
а по возмущающему воздействию при g(t)=0 будет иметь вид

. (7.16)

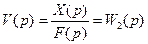
Замкнем систему, т.е. вновь подключим выход звена W₂(p) к сумматору (рис.7.5,а).

Рис.7.5. Преобразование структурной схемы САУ

Рассмотрим поведение системы при задающем воздействии и при f(t)=0. Тогда структурная схема САУ примет вид, как показано на рис.7.5,в, а передаточная функция замкнутой системы по задающему воздействию примет вид

. (7.17)

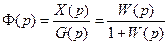
Определим выражение для передаточной функции замкнутой системы по ошибке. Поведение системы рассматривается только при задающем воздействии, а выходной величиной системы является ошибка e (рис.7.5,г). Тогда передаточная функция замкнутой системы по ошибке равна

. (7.18)

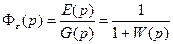
Сравнивая выражения (7.17) и (7.18), можно записать

Полученные выражения (7.17), (7.18) устанавливают связь между передаточной функцией разомкнутой САУ и передаточными функциями замкнутой системы соответственно по задающему воздействию и по сигналу ошибки.

Рассмотрим поведение системы только при возмущающем воздействии, т.е. g(t)=0. Тогда структурная схема системы примет вид, изображенный на рис.7.5,д, а передаточная функция замкнутой системы по возмущающему воздействию будет

. (7.19)

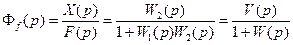
Выражение (7.19) определяет связь между передаточной функцией замкнутой системы по возмущающему воздействию и передаточными функциями разомкнутой системы.

По передаточной функции разомкнутой системы по задающему воздействию можно определить характеристические полиномы и характеристические уравнения системы в разомкнутом и замкнутом состояниях. Передаточная функция W(p) может быть представлена как отношение двух многочленов:

, (7.20)

(7.21)

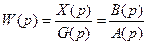
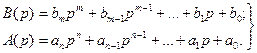
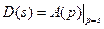
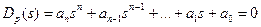
Многочлен является характеристическим полиномом разомкнутой системы. Таким образом, характеристическое уравнение разомкнутой системы можно получить из многочлена знаменателя передаточной функции W(p) (7.20), заменив переменную и приравняв полученное выражение к нулю, т.е. D_р(s)=0. Следовательно, характеристическое уравнение разомкнутой системы имеет вид:

. (7.22)

Аналогично может быть получено характеристическое уравнение замкнутой системы. Так как

, (7.23)

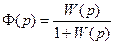
то, подставив выражение (7.20) в (7.23), получим

. (7.24)

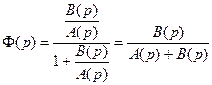
Таким образом, характеристическое уравнение замкнутой системы будет иметь вид:

Выражение (7.26) показывает, что характеристическое уравнение замкнутой системы можно получить по передаточной функции разомкнутой системы. Для этого необходимо просуммировать многочлен числителя и знаменателя передаточной функции W(p), заменить переменную и полученное выражение приравнять к нулю.

Вполне очевидно, что характеристическое уравнение как замкнутой, так и разомкнутой систем имеет одну и ту же степень.

Из выражений (7.17), (7.18) и (7.19) видим, что знаменатели этих выражениий одинаковые. Поэтому характеристическое уравнение замкнутой системы может быть получено по любой из передаточных функций замкнутой системы.

Видео:23) Построение Л.А.Ч.Х. и Л.Ф.Ч.Х. системы по её передаточной функцииСкачать

Типовые передаточные функции и характеристическое уравнение

Для описания системы вводят передаточные функции, связывающие определенные входы и выходы.

1. Передаточная функция разомкнутой системы определяется как произведение всех передаточных функций по основному контуру. Она единственная и не зависит от точки размыкания:

2. Передаточная функция замкнутой системы по задающему воздействию определяется как отношение изображения выходной координаты (в данном случае – скорости вращения двигателя) к изображению задающего воздействия:

3. Передаточная функция замкнутой системы по возмущающему воздействию определяется как отношение изображения выходной координаты к изображению возмущающего воздействия (в данном случае – момента нагрузки):

Стандартная схема системы

В целях унификации вводится стандартная структурная схема системы с единичной обратной связью, стандартными обозначениями входов и выходов и типовых передаточных функций.

Y(s)

F(s)

V(s)

W(s)

E(s)

Рисунок 7.2. стандартная схема системы

1. Передаточная функция разомкнутой системы:

и состоят из сомножителей не выше второго порядка.

– характеристическое уравнение разомкнутой системы, его корни определяют свойства разомкнутой системы.

2. Передаточная функция по задающему воздействию:

Приравниваем знаменатель к нулю, получаем характеристическое уравнение замкнутой системы.

– характеристическое уравнение замкнутой системы, его корни определяют свойства замкнутой системы.

3. Передаточная функция по возмущению:

4. Передаточная функция по ошибке:

Понятие устойчивости

Очень важно изучить поведение системы во времени. В некоторых случаях процессы оказываются расходящимися, что свидетельствует о неустойчивости системы.

Для нормальной эксплуатации система должна быть устойчивой, т.е. после действия возмущения она должна возвращаться в состояние равновесия.

В качестве примера рассмотрим поведение шарика на вогнутой поверхности (желоб), выпуклой поверхности и плоской поверхности.

Устойчивая система (вогнутая поверхность), процесс сходится:

x₀

Неустойчивая система (выпуклая поверхность), процесс расходится:

x₀

Нейтральная система (горизонтальная поверхность), координата (процесс) остается постоянной.

x₀

Эти примеры являются механической аналогией понятия устойчивости. Рассмотрим математическое определение понятия устойчивости.

u(t)

Д.У.

y(t)

U(s)

W(s)

Y(s)

Система описывается дифференциальным уравнением:

– решение дифференциального уравнения.

–однородное уравнение определяет свободную составляющую решения .

– корни характеристического уравнения.

– частное решение неоднородного дифференциального уравнения, определяется видом внешней функции;

– постоянные коэффициенты, определяются из начальных условий и полного (общего) решения.

Строго устойчивость определяется в смысле Ляпунова. Для линейных систем с постоянными параметрами считается, что система устойчива, если предел свободной составляющей равен 0

Устойчивость — внутреннее свойство системы, присущее ей вне зависимости от действующих на нее сигналов, поэтому рассматривается только свободная составляющая.

Это есть определение асимптотической устойчивости.

Свяжем требование устойчивости с расположением корней характеристического уравнения: