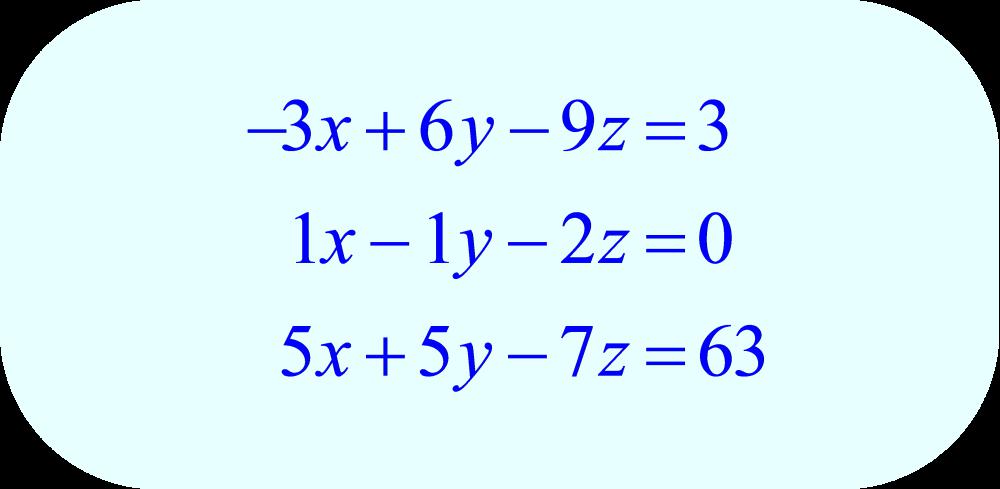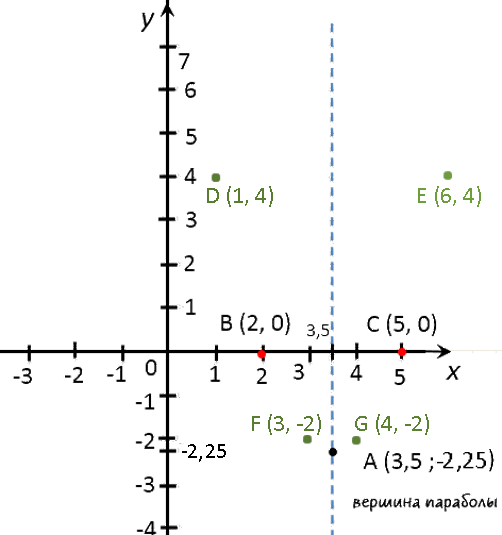Как показать на графике что уравнение не имеет корней

Решение уравнений в математике занимает особое место. Этому процессу предшествует множество часов изучения теории, в ходе которых ученик узнает способы решения уравнений, определения их вида и доводит навык до полного автоматизма. Однако далеко не всегда поиск корней имеет смысл, так как их может попросту не быть. Существуют особые приемы нахождения корней. В данной статье мы разберем основные функции, их области определения, а также случаи, когда их корни отсутствуют.

Какое уравнение не имеет корней?

Уравнение не имеет корней в том случае, если не существует таких действительных аргументов х, при которых уравнение тождественно верно. Для неспециалиста данная формулировка, как и большинство математических теорем и формул, выглядит очень размытой и абстрактной, однако это в теории. На практике все становится предельно просто. Например: уравнение 0 * х = -53 не имеет решения, так как не найдется такого числа х, произведение которого с нулем дало бы что-то, кроме нуля.

Сейчас мы рассмотрим самые базовые типы уравнений.

1. Линейное уравнение

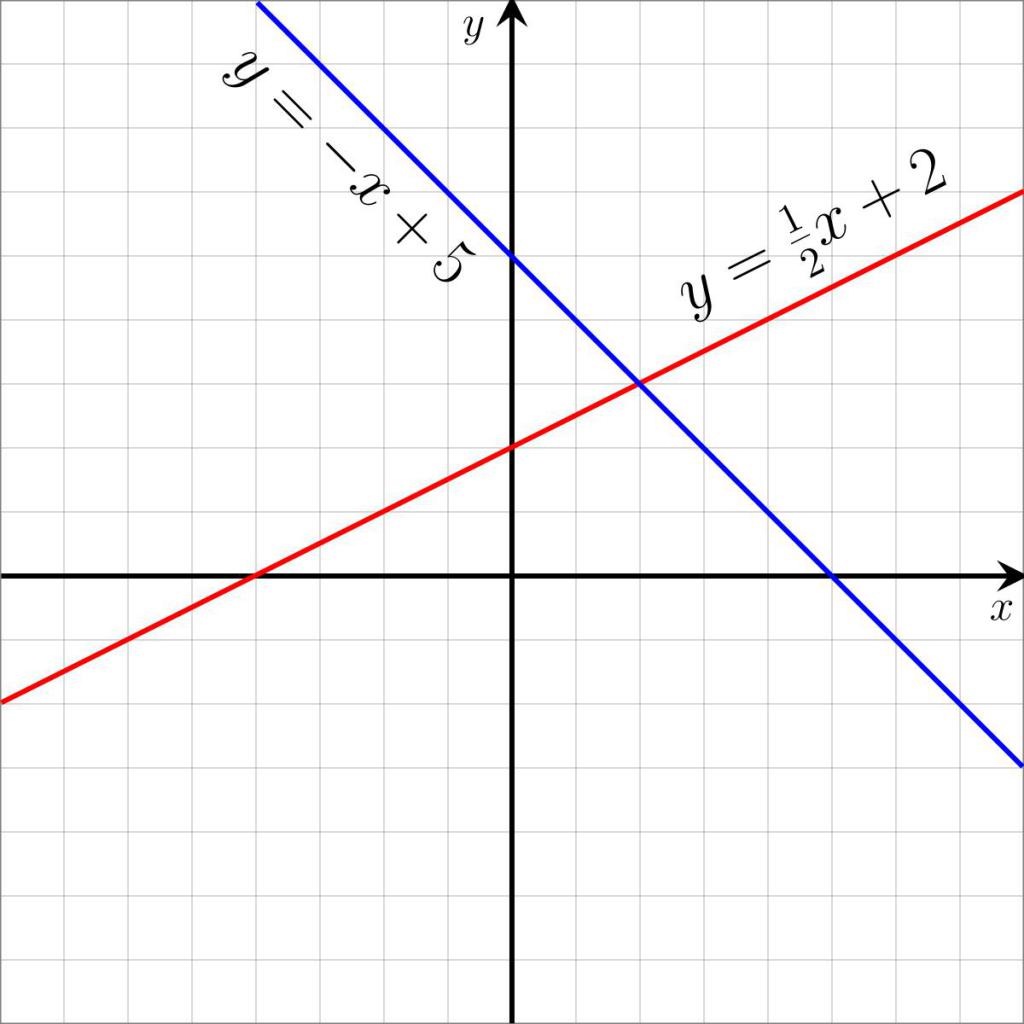
Уравнение называется линейным, если его правая и левая части представлены в виде линейных функций: ax + b = cx + d или в обобщенном виде kx + b = 0. Где а, b, с, d — известные числа, а х — неизвестная величина. Какое уравнение не имеет корней? Примеры линейных уравнений представлены на иллюстрации ниже.

В основном линейные уравнения решаются простым переносом числовой части в одну часть, а содержимого с х — в другую. Получается уравнение вида mx = n, где m и n — числа, а х — неизвестное. Чтобы найти х, достаточно разделить обе части на m. Тогда х = n/m. В основном линейные уравнения имеют только один корень, однако бывают случаи, когда корней либо бесконечно много, либо нет вовсе. При m = 0 и n = 0 уравнение принимает вид 0 * х = 0. Решением такого уравнения будет абсолютно любое число.

Однако какое уравнение не имеет корней?

При m = 0 и n = 0 уравнение не имеет корней из множества действительных чисел. 0 * х = -1; 0 * х = 200 — эти уравнения не имеют корней.

2. Квадратное уравнение

Квадратным уравнением называется уравнение вида ax 2 + bx + c = 0 при а = 0. Самым распространенным способом решения квадратного уравнения является решение через дискриминант. Формула нахождения дискриминанта квадратного уравнения: D = b 2 — 4 * a * c. Далее находится два корня х_1,2= (-b ± √D) / 2 * a.

При D > 0 уравнение имеет два корня, при D = 0 — корень один. Но какое квадратное уравнение не имеет корней? Пронаблюдать количество корней квадратного уравнения проще всего по графику функции, представляющем собой параболу. При а > 0 ветви направлены вверх, при а 2 – 8x + 72 = 0 не имеет корней, так как имеет отрицательный дискриминант D = (–8) 2 – 4 * 1 * 72 = -224. Это значит, что парабола не касается оси абсцисс и функция никогда не принимает значение 0, следовательно, уравнение не имеет действительных корней.

3. Тригонометрические уравнения

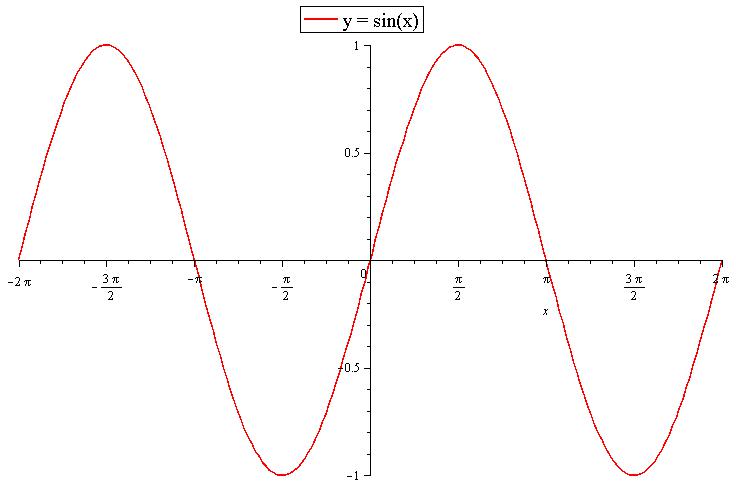
Тригонометрические функции рассматриваются на тригонометрической окружности, однако могут быть представлены и в декартовой системе координат. В данной статье мы рассмотрим две основные тригонометрические функции и их уравнения: sinx и cosx. Так как данные функции образуют тригонометрическую окружность с радиусом 1, |sinx| и |cosx| не могут быть больше 1. Итак, какое уравнение sinx не имеет корней? Рассмотрим график функции sinx, представленный на картинке ниже.

Мы видим, что функция является симметричной и имеет период повторения 2pi. Исходя их этого, можно говорить, что максимальным значением этой функции может быть 1, а минимальным -1. Например, выражение cosx = 5 не будет иметь корней, так как по модулю оно больше единицы.

Это самый простой пример тригонометрических уравнений. На самом деле их решение может занимать множество страниц, в конце которых вы осознаете, что использовали неправильную формулу и все нужно начинать сначала. Порой даже при правильном нахождении корней вы можете забыть учесть ограничения по ОДЗ, из-за чего в ответе появляется лишний корень или интервал, и весь ответ обращается в ошибочный. Поэтому строго следите за всеми ограничениями, ведь не все корни вписываются в рамки задачи.

4. Системы уравнений

Система уравнений представляет собой совокупность уравнений, объединенных фигурной или квадратной скобками. Фигурные скобки обозначают совместное выполнение всех уравнений. То есть если хотя бы одно из уравнений не имеет корней или противоречит другому, вся система не имеет решения. Квадратные скобки обозначают слово «или». Это значит, что если хотя бы одно из уравнений системы имеет решение, то вся система имеет решение.

Ответом системы с квадратными скобками является совокупность всех корней отдельных уравнений. А системы с фигурным скобками имеют только общие корни. Системы уравнений могут включать абсолютно разнообразные функции, поэтому такая сложность не позволяет сказать сразу, какое уравнение не имеет корней.

Обобщение и советы по нахождению корней уравнения

В задачниках и учебниках встречаются разные типы уравнений: такие, которые имею корни, и не имеющие их. В первую очередь, если у вас не получается найти корни, не думайте, что их нет совсем. Возможно, вы совершили где-нибудь ошибку, тогда достаточно лишь внимательно перепроверить ваше решение.

Мы рассмотрели самые базовые уравнения и их виды. Теперь вы можете сказать, какое уравнение не имеет корней. В большинстве случаев сделать это совсем не трудно. Для достижения успеха в решении уравнений требуется лишь внимание и сосредоточенность. Практикуйтесь больше, это поможет вам ориентироваться в материале гораздо лучше и быстрее.

Итак, уравнение не имеет корней, если:

• в линейном уравнении mx = n значение m = 0 и n = 0;
• в квадратном уравнении, если дискриминант меньше нуля;
• в тригонометрическом уравнении вида cosx = m / sinx = n, если |m| > 0, |n| > 0;
• в системе уравнений с фигурными скобками, если хотя бы одно уравнение не имеет корней, и с квадратными скобками, если все уравнения не имеют корней.

Квадратичная функция и ее график

В этой статье мы поговорим о том, что такое квадратичная функция, научимся строить ее график и определять вид графика в зависимости от знака дискриминанта и знака старшего коэффициента.
Итак.

Функция вида , где 0″ title=»a0″/> называется квадратичной функцией.

В уравнении квадратичной функции:

a — старший коэффициент

b — второй коэффициент

с — свободный член.

Графиком квадратичной функции является квадратичная парабола, которая для функции имеет вид:

Обратите внимание на точки, обозначенные зелеными кружками — это, так называемые «базовые точки». Чтобы найти координаты этих точек для функции , составим таблицу:

Внимание! Если в уравнении квадратичной функции старший коэффициент , то график квадратичной функции имеет ровно такую же форму, как график функции при любых значениях остальных коэффициентов.

График функции имеет вид:

Для нахождения координат базовых точек составим таблицу:

Обратите внимание, что график функции симметричен графику функции относительно оси ОХ.

Итак, мы заметили:

Если старший коэффициент a>0 , то ветви параболы напрaвлены вверх .

Если старший коэффициент a , то ветви параболы напрaвлены вниз .

Второй параметр для построения графика функции — значения х, в которых функция равна нулю, или нули функции. На графике нули функции — это точки пересечения графика функции с осью ОХ.

Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю, чтобы найти координаты точек пересечения графика функции с осью ОХ, нужно решить уравнение .

В случае квадратичной функции нужно решить квадратное уравнение .

В процессе решения квадратного уравнения мы находим дискриминант: , который определяет число корней квадратного уравнения.

И здесь возможны три случая:

1. Если ,то уравнение не имеет решений, и, следовательно, квадратичная парабола не имеет точек пересечения с осью ОХ. Если 0″ title=»a>0″/>,то график функции выглядит как-то так:

2. Если ,то уравнение имеет одно решение, и, следовательно, квадратичная парабола имеет одну точку пересечения с осью ОХ. Если 0″ title=»a>0″/>,то график функции выглядит примерно так:

3 . Если 0″ title=»D>0″/>,то уравнение имеет два решения, и, следовательно, квадратичная парабола имеет две точки пересечения с осью ОХ:

,

Если 0″ title=»a>0″/>,то график функции выглядит примерно так:

Следовательно, зная направление ветвей параболы и знак дискриминанта, мы уже можем в общих чертах определить, как выглядит график нашей функции.

Следующий важный параметр графика квадратичной функции — координаты вершины параболы:

Прямая, проходящая через вершину параболы параллельно оси OY является осью симметрии параболы.

И еще один параметр, полезный при построении графика функции — точка пересечения параболы с осью OY.

Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы с осью OY, нужно в уравнение параболы вместо х подставить ноль: .

То есть точка пересечения параболы с осью OY имеет координаты (0;c).

Итак, основные параметры графика квадратичной функции показаны на рисунке:

Рассмотрим несколько способов построения квадратичной параболы. В зависимости от того, каким образом задана квадратичная функция, можно выбрать наиболее удобный.

1. Функция задана формулой .

Рассмотрим общий алгоритм построения графика квадратичной параболы на примере построения графика функции

1. Направление ветвей параболы.

Так как 0″ title=»a=2>0″/>,ветви параболы направлены вверх.

2. Найдем дискриминант квадратного трехчлена

0″ title=»D=b^2-4ac=9-4*2*(-5)=49>0″/>

Дискриминант квадратного трехчлена больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ.

Для того, чтобы найти их координаты, решим уравнение:

,

3. Координаты вершины параболы:

4. Точка пересечения параболы с осью OY: (0;-5),и ей симметричная относительно оси симметрии параболы.

Нанесем эти точки на координатную плоскость, и соединим их плавной кривой:

Этот способ можно несколько упростить.

1. Найдем координаты вершины параболы.

2. Найдем координаты точек, стоящих справа и слева от вершины.

Воспользуемся результатами построения графика функции

Кррдинаты вершины параболы

Ближайшие к вершине точки, расположенные слева от вершины имеют абсциссы соответственно -1;-2;-3

Ближайшие к вершине точки, расположенные справа имеют абсциссы соответственно 0;1;2

Подставим значения х в уравнение функции, найдем ординаты этих точек и занесем их в таблицу:

Нанесем эти точки на координатную плоскость и соединим плавной линией:

2 . Уравнение квадратичной функции имеет вид — в этом уравнении — координаты вершины параболы

или в уравнении квадратичной функции , и второй коэффициент — четное число.

Построим для примера график функции .

Вспомним линейные преобразования графиков функций. Чтобы построить график функции , нужно

• сначала построить график функции ,
• затем одинаты всех точек графика умножить на 2,
• затем сдвинуть его вдоль оси ОХ на 1 единицу вправо,
• а затем вдоль оси OY на 4 единицы вверх:

Теперь рассмотрим построение графика функции . В уравнении этой функции , и второй коэффициент — четное число.

Выделим в уравнении функции полный квадрат:

Следовательно, координаты вершины параболы: . Старший коэффициент равен 1, поэтому построим по шаблону параболу с вершиной в точке (-2;1):

3 . Уравнение квадратичной функции имеет вид y=(x+a)(x+b)

Построим для примера график функции y=(x-2)(x+1)

1. Вид уравнения функции позволяет легко найти нули функции — точки пересечения графика функции с осью ОХ:

(х-2)(х+1)=0, отсюда

2. Координаты вершины параболы:

3. Точка пересечения с осью OY: с=ab=(-2)(1)=-2 и ей симметричная.

Нанесем эти точки на координатную плоскость и построим график:

График квадратичной функции.

Перед вами график квадратичной функции вида .

Кликните по чертежу.
Подвигайте движки.
Исследуйте зависимость
— ширины графика функции от значения коэффициента ,
— сдвига графика функции вдоль оси от значения ,

— сдвига графика функции вдоль оси от значения
— направления ветвей параболы от знака коэффициента
— координат вершины параболы от значений и :

И.В. Фельдман, репетитор по математике.

График функции неполного квадратного уравнения

Прежде чем перейти к разбору квадратичной функции рекомендуем вспомнить, что называют функцией в математике.

Если вы прочно закрепите общие знания о функции (способы задания, понятие графика) дальнейшее изучение других видов функций будет даваться значительно легче.

Что называют квадратичной функцией

Квадратичная функция — это функция вида

Другими словами можно сказать, что если в функции старшая (то есть самая большая) степень, в которой стоит « x » — это « 2 », то перед нами квадратичная функция.

Рассмотрим примеры квадратичных функций и определим, чему в них равны коэффициенты « a », « b » и « с ».

Квадратичная функция	Коэффициенты
y = 2x 2 − 7x + 9	a = 2 b = −7 с = 9
y = 3x 2 − 1	a = 3 b = 0 с = −1
y = −3x 2 + 2x	a = −3 b = 2 с = 0

Как построить график квадратичной функции

График квадратичной функции называют параболой.

Парабола выглядит следующим образом.

Также парабола может быть перевернутой.

Существует четкий алгоритм действий при построении графика квадратичной функции. Рекомендуем при построении параболы всегда следовать этому порядку действий, тогда вы сможете избежать ошибок при построении.

Чтобы было проще понять этот алгоритм, сразу разберем его на примере.

Построим график квадратичной функции « y = x 2 −7x + 10 ».

Направление ветвей параболы

Если « a > 0 », то ветви направлены вверх.

Если « a », то ветви направлены вниз.

В нашей функции « a = 1 », это означает, что ветви параболы направлены вверх.

Координаты вершины параболы

Чтобы найти « x » (координата вершины по оси « Ox ») нужно использовать формулу:

−b

2a

Найдем « x » для нашей функции « y = x 2 −7x + 10 ».

− (−7)

2 · 1

7

2

Теперь нам нужно найти « y » (координату вершины по оси « Oy »). Для этого нужно подставить найденное значение « x » в исходную функцию. Вспомнить, как найти значение функции можно в уроке «Как решать задачи на функцию» в подразделе «Как получить значение функции».

Выпишем полученные координаты вершины параболы.

(·) A (3,5; −2,25) — вершина параболы.

Отметим вершину параболы на системе координат. Проведем через отмеченную точку ось симметрии, так как парабола — это симметричный график относительно оси « Oy ».

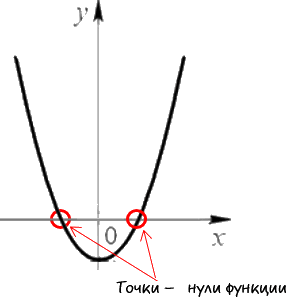
Для начала давайте разберемся, что называют нулями функции.

Нули функции — это точки пересечения графика функции с осью « Ox » (осью абсцисс).

Наглядно нули функции на графике выглядят так:

Свое название нули функции получили из-за того, что у этих точек координата по оси « Oy » равна нулю.

Теперь давайте разберемся, как до построения графика функции рассчитать координаты точек нулей функции.

Чтобы найти координаты точек нулей функции, нужно в исходную функцию подставить вместо « y = 0 ».

Подставим в заданную функцию « y = x 2 −7x + 10 » вместо « y = 0 » и решим полученное квадратное уравнение относительно « x » .

0 = x 2 −7x + 10
x 2 −7x + 10 = 0
x_1;2 =

7 ± √ 49 − 4 · 1 · 10

2 · 1

7 ± √ 9

2

7 ± 3

2

x1 =

7 + 3

2

x₂ =

7 − 32x₁ =

102x₂ =

42x₁ = 5x₂ = 2

Мы получили два корня в уравнении, значит, у нас две точки пересечения с осью « Ox ». Назовем эти точки и выпишем их координаты.

Отметим полученные точки («нули функции») на системе координат.

Возьмем четыре произвольные числовые значения для « x ». Целесообразно брать целые числовые значения на оси « Ox », которые наиболее близки к оси симметрии. Числа запишем в таблицу в порядке возрастания.

x	1	3	4	6
y

Для каждого выбранного значения « x » рассчитаем « y ».

• y(1) = 1 2 − 7 · 1 + 10 = 1 − 7 + 10 = 4
• y(3) = 3 2 − 7 · 3 + 10 = 9 − 21 + 10 = −2
• y(4) = 4 2 − 7 · 4 + 10 = 16 − 28 + 10 = −2
• y(6) = 6 2 − 7 · 6 + 10 = 36 − 42 + 10 = 4

Запишем полученные результаты в таблицу.

x	1	3	4	6
y	4	−2	−2	4

Отметим полученные точки графика на системе координат (зеленые точки).

Теперь мы готовы построить график. На забудьте после построения подписать график функции.

Краткий пример построения параболы

Рассмотрим другой пример построения графика квадратичной функции. Только теперь запишем алгоритм построения коротко без подробностей.

Пусть требуется построить график функции « y = −3x 2 − 6x − 4 ».

Направление ветвей параболы « a = −3 » — ветви параболы направлены вниз.

Координаты вершины параболы

−b

2a

−(−6)

2 · (−3)

6

−6

y (−1) = (−3) · (−1) 2 − 6 · (−1) − 4 = −3 · 1 + 6 − 4 = −1

(·) A (−1; −1) — вершина параболы.

Точки пересечения с осью « Ox » ( y = 0 ).

−3x 2 − 6x − 4 = 0 |·(−1)

−6 ± √ 6 2 − 4 · 3 · 4

2 · 1

−6 ± √ 36 − 48

2

−6 ± √ −12

2

Ответ: нет действительных корней.

Так как корней нет, значит, график функции не пересекает ось « Ox ».

Вспомогательные точки для: « x = −3 »; « x = −2 »; « x = 0 »; « x = 1 ». Подставим в исходную функцию « y = −3x 2 − 6x − 4 ».

• y(−3) = −3 · (−3) 2 − 6 · (−3) − 4 = −3 · 9 + 18 − 4 = −27 + 14 = −13
• y(−2) = −3 · (−2) 2 − 6 · (−2) − 4 = −3 · 4 + 12 − 4 = −12 + 12 − 4 = −4
• y(0) = −3 · 0 2 − 6 · 0 − 4 = −4
• y(1) = −3 · 1 2 − 6 · 1 − 4 = −3 −6 − 4 = −13

x	−3	−2	1
y	−13	−4	−4	−13

Отметим вспомогательные точки. Отмечаем на системе координат только те точки, которые не выходят за масштаб нашей системы координат, то есть точки « (−2; −4) » и « (0; −4) ». Построим и подпишем график функции.

Урок: как построить параболу или квадратичную функцию?

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Парабола — это график функции описанный формулой ax 2 +bx+c=0.
Чтобы построить параболу нужно следовать простому алгоритму действий:

1 ) Формула параболы y=ax 2 +bx+c,
если а>0 то ветви параболы направленны вверх,
а 2 +bx+c=0;

a) Полное квадратное уравнение имеет вид ax 2 +bx+c=0 и решается по дискриминанту;
b) Неполное квадратное уравнение вида ax 2 +bx=0. Чтобы его решить нужно вынести х за скобки, потом каждый множитель приравнять к 0:
ax 2 +bx=0,
х(ax+b)=0,
х=0 и ax+b=0;
c)Неполное квадратное уравнение вида ax 2 +c=0. Чтобы его решить нужно неизвестные перенести в одну сторону, а известные в другую. x =±√(c/a);

4) Найти несколько дополнительных точек для построения функции.

ПРАКТИЧЕСКАЯ ЧАСТЬ

И так теперь на примере разберем все по действиям:
Пример №1:
y=x 2 +4x+3
c=3 значит парабола пересекает OY в точке х=0 у=3. Ветви параболы смотрят вверх так как а=1 1>0.
a=1 b=4 c=3 x=(-b)/2a=(-4)/(2*1)=-2 y= (-2) 2 +4*(-2)+3=4-8+3=-1 вершина находится в точке (-2;-1)
Найдем корни уравнения x 2 +4x+3=0
По дискриминанту находим корни
a=1 b=4 c=3
D=b 2 -4ac=16-12=4
x=(-b±√(D))/2a
x₁=(-4+2)/2=-1
x₂=(-4-2)/2=-3

Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=-2

х -4 -3 -1 0
у 3 0 0 3

Подставляем вместо х в уравнение y=x 2 +4x+3 значения
y=(-4) 2 +4*(-4)+3=16-16+3=3
y=(-3) 2 +4*(-3)+3=9-12+3=0
y=(-1) 2 +4*(-1)+3=1-4+3=0
y=(0) 2 +4*(0)+3=0-0+3=3
Видно по значениям функции,что парабола симметрична относительно прямой х=-2

Пример №2:
y=-x 2 +4x
c=0 значит парабола пересекает OY в точке х=0 у=0. Ветви параболы смотрят вниз так как а=-1 -1 2 +4*2=-4+8=4 вершина находится в точке (2;4)
Найдем корни уравнения -x 2 +4x=0
Неполное квадратное уравнение вида ax 2 +bx=0. Чтобы его решить нужно вынести х за скобки, потом каждый множитель приравнять к 0.
х(-x+4)=0, х=0 и x=4.

Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=2
х 0 1 3 4
у 0 3 3 0
Подставляем вместо х в уравнение y=-x 2 +4x значения
y=0 2 +4*0=0
y=-(1) 2 +4*1=-1+4=3
y=-(3) 2 +4*3=-9+13=3
y=-(4) 2 +4*4=-16+16=0
Видно по значениям функции,что парабола симметрична относительно прямой х=2

Пример №3
y=x 2 -4
c=4 значит парабола пересекает OY в точке х=0 у=4. Ветви параболы смотрят вверх так как а=1 1>0.
a=1 b=0 c=-4 x=(-b)/2a=0/(2*(1))=0 y=(0) 2 -4=-4 вершина находится в точке (0;-4)
Найдем корни уравнения x 2 -4=0
Неполное квадратное уравнение вида ax 2 +c=0. Чтобы его решить нужно неизвестные перенести в одну сторону, а известные в другую. x =±√(c/a)
x 2 =4
x₁=2
x₂=-2

Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=0
х -2 -1 1 2
у 0 -3 -3 0
Подставляем вместо х в уравнение y= x 2 -4 значения
y=(-2) 2 -4=4-4=0
y=(-1) 2 -4=1-4=-3
y=1 2 -4=1-4=-3
y=2 2 -4=4-4=0
Видно по значениям функции,что парабола симметрична относительно прямой х=0

Подписывайтесь на канал на YOUTUBE, чтобы быть в курсе всех новинок и готовится с нами к экзаменам.

График квадратного уравнения вида ax 2 + bx + c или a(x – h) 2 + k представляет собой параболу (U-образную кривую). Для построения графика такого уравнения необходимо найти вершину параболы, ее направление и точки пересечения с осями Х и Y. Если вам дано относительно простое квадратное уравнение, то вы можете подставить в него разные значения «х», найти соответствующие значения «у» и построить график.

Как показать на графике что уравнение не имеет корней

Покажем, как задачи с параметрами можно решать графически.

Найдём количество решений уравнения

в зависимости от $$ a$$.

Искомое количество решений совпадает с числом точек пересечения графиков функций

График первой функции получается из графика функции, который был построен в предыдущем примере. Для этого нужно воспользоваться преобразованием вида ПР1 то есть график $$ y=_left(xright)$$ имеет такой вид, как показано на рис. 43 $$ fleft(0right)=sqrt$$.

Графиком функции $$ y=a$$ будет прямая, параллельная оси $$ Ox$$ (рис. 43). При этом она пересекает ось ординат в точке $$ (0,a)$$. Легко видеть, что при $$a 3$$ прямая $$ y=a$$ не имеет пересечений с графиком $$ y=_left(xright)$$, при $$ a=3$$ и $$ ain [0;sqrt)$$ есть две точки пересечения, а при $$ ain [sqrt;3)$$ – четыре общие точки и при $$ a=sqrt$$ – три общие точки. Остаётся лишь сформулировать ответ.

При $$ ain (-infty ;0)bigcup (3;+infty )$$ решений нет, при $$ ain [0;sqrt)bigcup left$$ – два решения, при $$ ain left<sqrtright>$$ – три решения, при $$ ain (sqrt;3)$$ – четыре решения.

Найдём количество решений уравнения в зависимости от $$ a$$:

Методом интервалов нетрудно построить график функции

Количество решений уравнения совпадает с числом точек пересечения этого графика с прямой $$ fleft(xright)=a$$ (рис. 44).

Проанализировав график, несложно выписать ответ.

При $$ ain (8;+infty )$$ уравнение имеет 2 решения, при $$ a=8$$ уравнение имеет бесконечно много решений, при $$ ain (-infty ;8)$$ решений нет.

Рассмотрим ещё один пример задач с параметром, где используется построение множеств, задаваемых уравнениями с модулем. Напомним, что графиком уравнения называют линию на плоскости, на которой лежат те и только те точки, координаты которых удовлетворяют этому уравнению.

Найдём количество решений системы уравнений

в зависимости от $$ a$$.

Для решения необходимо построить график уравнения $$ left|xright|+left|yright|=4$$. Это можно сделать, последовательно выполнив построения таких графиков:

График второго уравнения – окружность с центром в точке $$ O(0;0)$$ и радиусом $$ left|aright|$$. Изобразим оба этих графика на координатной плоскости $$ xOy$$.

Как видим, при $$|a| 4$$ графики не пересекаются. При $$ left|aright|=2sqrt$$ или $$ left|aright|=4$$ есть 4 точки пересечения. При остальных $$ a$$ есть 8 точек пересечения. Таким образом, можно сформулировать ответ.

При $$ ain (-infty ;-4)cup (-2sqrt;2sqrt)cup (4;+infty )$$ система не имеет решений;

при $$ ain <-4;-2sqrt;2sqrt;4>$$ система имеет 4 решения;

при $$ ain (-4;-2sqrt)cup (2sqrt;4)$$ система имеет 8 решений.

В следующей задаче нам потребуется понятие локального экстремума функции. Говорят, что функция $$ y=fleft(xright)$$ имеет локальный максимум в точке $$ _$$, если для некоторого числа $$ε > 0$$ при $$|x − x_0| 0$$ при $$|x − x_0| 0$$ график $$ y=at-3$$ касается линии $$ y=sqrt$$ (cм. рис. 46). Уравнение $$ D=0$$ имеет единственный положительный корень `a=1/4`. Следовательно, `a_2=1/4`. Если $$dfrac3leq a 1/4` они не имеют общих точек.

Рассмотрим пример использования этого правила в задаче.

Найдём все значения параметра $$ a$$, при которых система

имеет хотя бы одно решение.

Неравенство системы после выделения полных квадратов можно записать в виде $$ ^-8left|xright|+16+^-8left|yright|+16le 1$$ или $$ left(right|x|-4^+(left|yright|-4^le 1$$. Множество $$ E$$ решений этого неравенства – объединение кругов $$ _$$, $$ _$$, $$ _$$, $$ _$$ (вместе с их границами) радиуса $$ 1$$ (см. рис. 47) с центрами $$ _(4;4)$$, $$ _(4;-4)$$, $$ _(-4;-4)$$, $$ _(-4;4)$$. Запишем уравнение системы в виде

Это уравнение задаёт окружность $$ L$$ радиуса $$ left|aright|$$ с центром в точке $$ M(0;1)$$, или точку $$ (0;1)$$ при $$ a=0$$. Исходная система имеет хотя бы одно решение при тех значениях $$ a$$, при которых окружность $$ L$$ имеет общие точки с множеством $$ E$$. При этом ввиду симметричного расположения соответствующих пар кругов относительно оси ординат достаточно выяснить, при каких значениях $$ a$$ окружность $$ L$$ имеет общие точки с кругами, центрами которых являются точки $$ _$$ и $$ _$$. Проведём из точки $$ M$$ лучи $$ _$$ и $$ _$$ в направлении точек $$ _$$ и $$ _$$. Пусть $$ _$$ и $$ _$$ – точки пересечения $$ _$$ и окружности с центром $$ _$$, $$ _$$ и $$ _$$ – точки пересечения $$ _$$ и окружности с центром $$ _$$. Тогда из геометрических соображений имеем:

При $$ 4le left|aright|le 6$$ окружность с центром $$ M$$ имеет общие точки с кругом $$ _$$ , а при $$ sqrt-1le left|aright|le sqrt+1$$ – с кругом $$ _$$.

а) Если $$b 0$$. Эта система не имеет решений при $$ a=0$$ и поэтому $$b 0$$. Теперь мы прибегнем к графическому методу. Рассмотрим два случая: $$0 1$$. Если $$b > 1$$, то $$sqrt Эта система не имеет решений, так как прямая $$ y=x-b$$ не пересекает график функции $$ y=|^-b|$$ (см. рис. 48). Если $$0 0$$).

В завершении разберём несколько задач с параметрами, которые удобно решать методом областей на координатной плоскости.

Найдём все значения `a`, при каждом из которых уравнение

Рассмотрим функции `f(x)-a|x-3|` и `g(x)=5/(x+2)`.

Если построить график функции `f(x)` для разных `a` (рис. 50) и график функции `g(x)` (рис. 51), то можно без проблем исследовать на промежутке `[0;+oo)` уравнение `f(x)=g(x)`.

При `a При `a>0` функция `f(x)` возрастает на промежутке `(3;+oo)`. Функция `g(x)` убывает на этом промежутке, поэтому уравнение `f(x)=g(x)` всегда имеет ровно одно решение на промежутке `(3;+oo)`, поскольку `f(3) g(3+1/a)`. На промежутке `[0;3]` уравнение `f(x)=g(x)` принимает вид `3a-ax=5/(x+2)`. Это уравнение сводится к уравнению `ax^2-ax+(5-6a)=0`. Будем считать, что `a>0`, поскольку случай `a

Пусть уравнение имеет два корня, то есть `a>4/5`. Тогда оба корня меньше `3`, поскольку при `x>=3` значения функции `3a-ax` неположительны, а значения функции `5/(x+2)` положительны. По теореме Виета сумма корней равна `1`, а произведение равно `5/6-6`. Значит, больший корень всегда принадлежит промежутку `[0;3]`, а меньший принадлежит этому промежутку тогда и только тогда, когда `5/a-6>=0`, то есть `a 5/6`;

– три корня при `4/5

В завершении разберём несколько задач с параметрами, которые удобно решать методом областей на координатной плоскости. В следующем примере будем использовать известный подход к задачам, содержащим некоторые переменные в квадрате. Суть этого подхода — рассмотрение выражения как квадратичной функции относительно какой-нибудь переменной (остальные переменные при этом считаются параметрами) с последующим использованием известных свойств квадратичной функции.

Найдём все значения параметра $$ a$$, при каждом из которых система уравнений

имеет ровно три решения.

Первое уравнение данной системы равносильно совокупности двух уравнений $$ |y+9|+|x+2|=2$$ и $$ ^+^=3$$. Первое из них задаёт квадрат $$ G$$ с центром $$ (-2;-9)$$, диагонали которого равны $$ 4$$ и параллельны осям координат. Второе задаёт окружность $$ S$$ с центром $$ (0;0)$$ радиуса $$ sqrt$$ (см. рис. 52).

Второе уравнение исходной системы при $$a > 0$$ задаёт окружность $$ Omega $$ с центром $$ (-2;-4)$$ радиуса $$ R=sqrt$$.

Отметим, что при $$a Рассмотрев случаи внешнего и внутреннего касания окружностей $$ Omega $$ и $$ S$$, можно заключить, что они имеют ровно `1` общую точку при $$ R=sqrtpm sqrt$$, ровно `2` общие точки при $$ Rin (sqrt-sqrt;sqrt+sqrt)$$ и ни одной общей точки при остальных $$ R$$. Поскольку центры окружности $$ Omega $$ и квадрата $$ G$$ лежат на прямой $$ x=-2$$, то $$ Omega $$ и $$ G$$ имеют ровно `1` общую точку при $$ R=3$$ или $$ R=7$$, ровно `2` общие точки при $$ Rin (3;7)$$ и ни одной общей точки при остальных значениях $$ R$$. Для того чтобы у системы было 3 решения, необходимо и достаточно, чтобы окружность $$ Omega $$ имела `2` общие точки с квадратом $$ G$$ и `1` общую точку с окружностью $$ S$$ или наоборот. Рассмотрим значения $$ R$$, при которых окружность $$ Omega $$ имеет с квадратом $$ G$$ или окружностью $$ S$$ ровно `1` общую точку.

1) $$ R=sqrt+sqrt$$. Тогда есть ровно `1` общая точка с окружностью $$ S$$, и ровно `2` общие точки с квадратом $$ G$$ (т. к. $$3 sqrt + sqrt$$), т. е. у системы 1 решение.

Итак, подходят $$ R=3$$ и $$ R=sqrt+sqrt$$. Тогда искомые значения параметра $$ a=^=9$$ и $$ a=(sqrt+sqrt^=23+4sqrt$$.

📽️ Видео