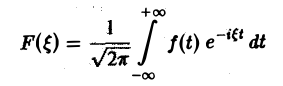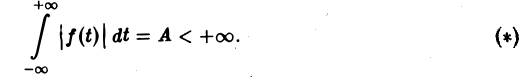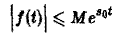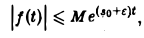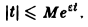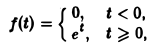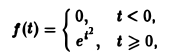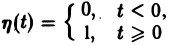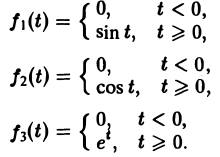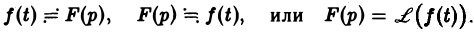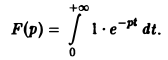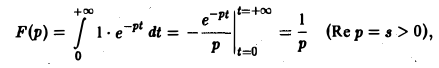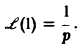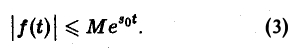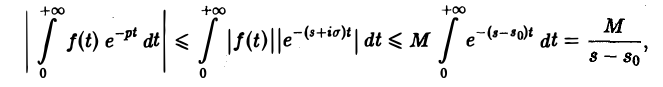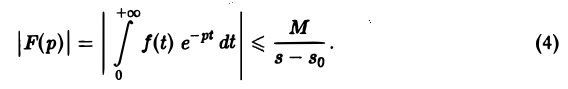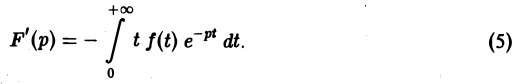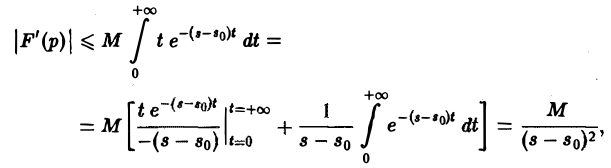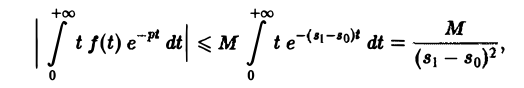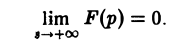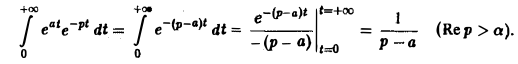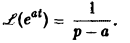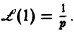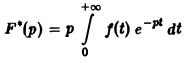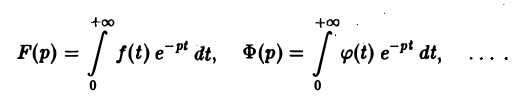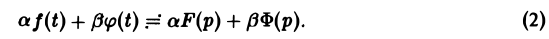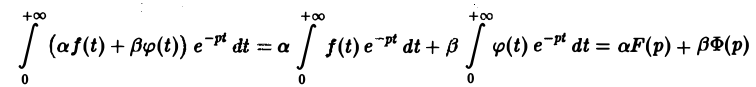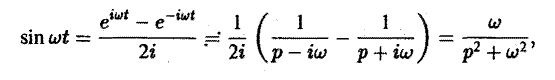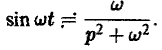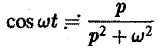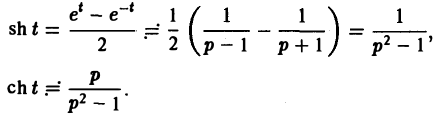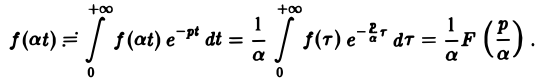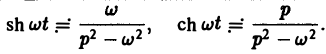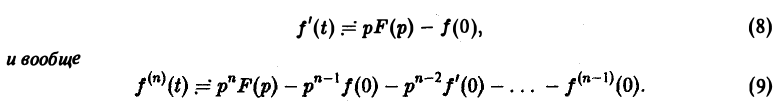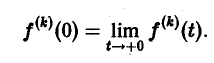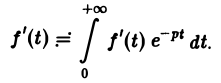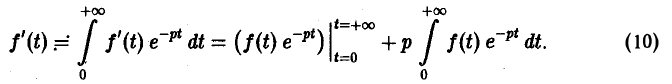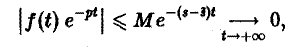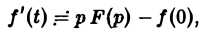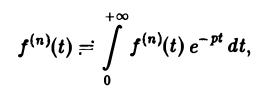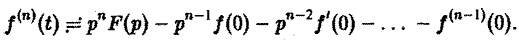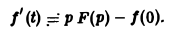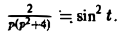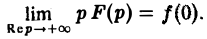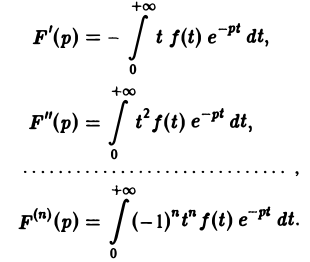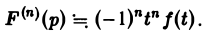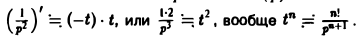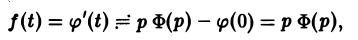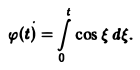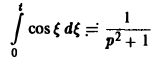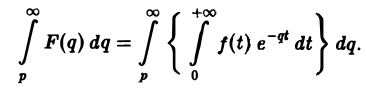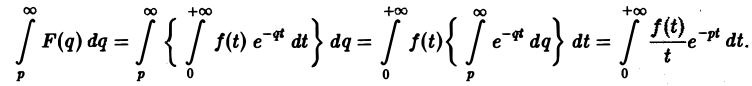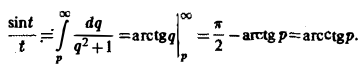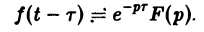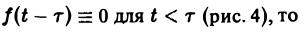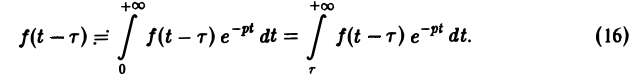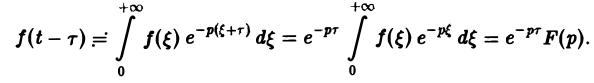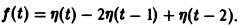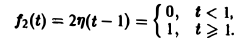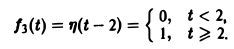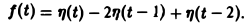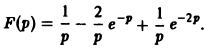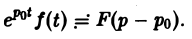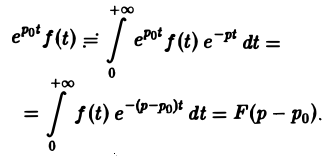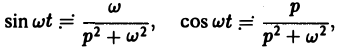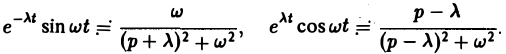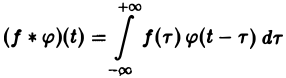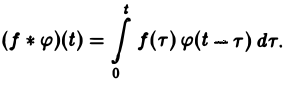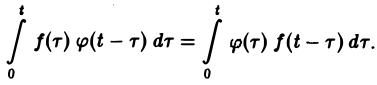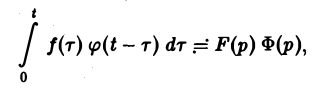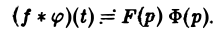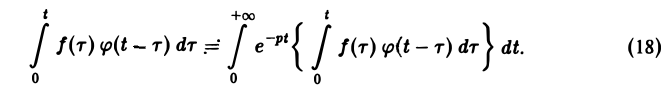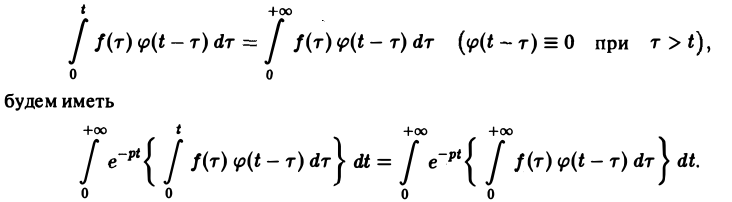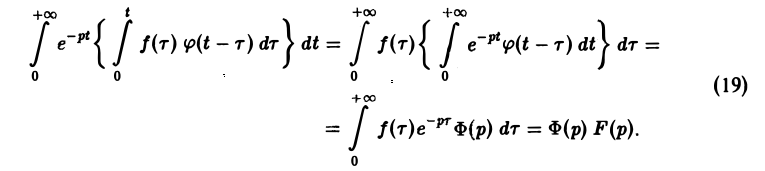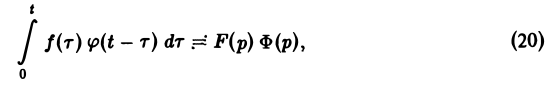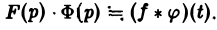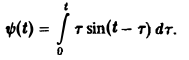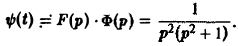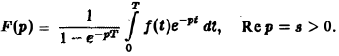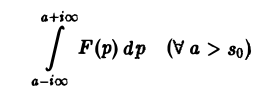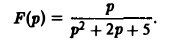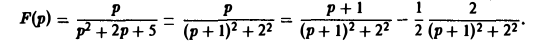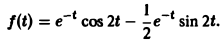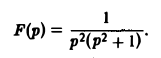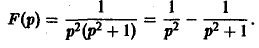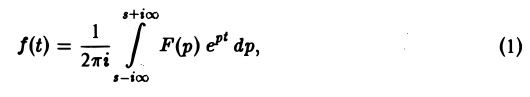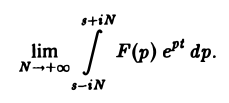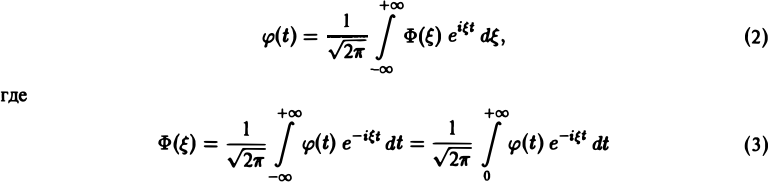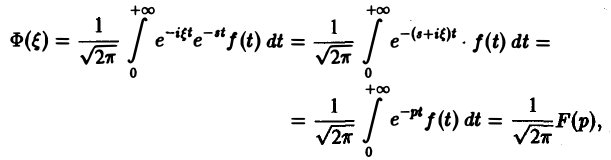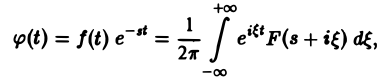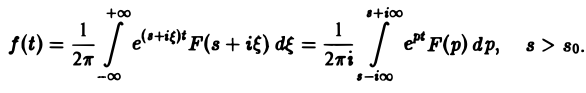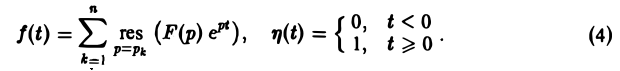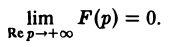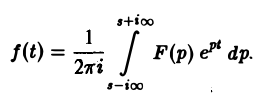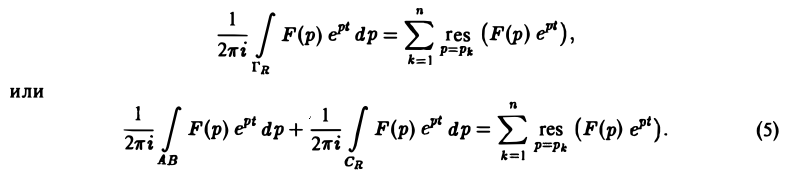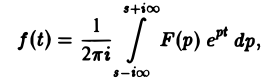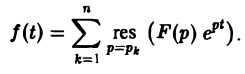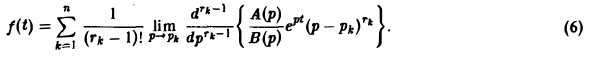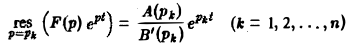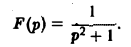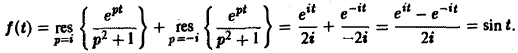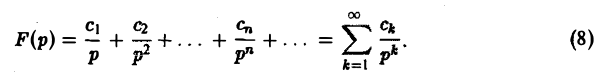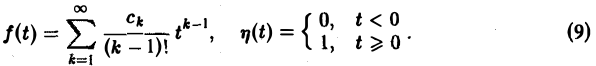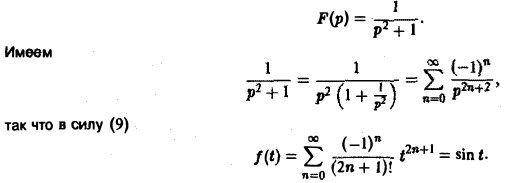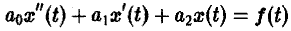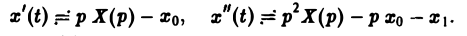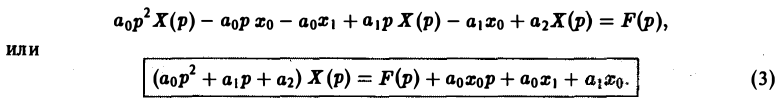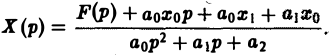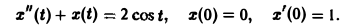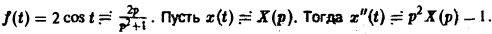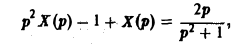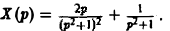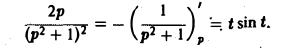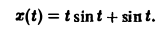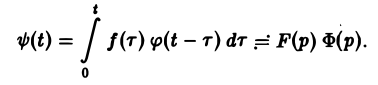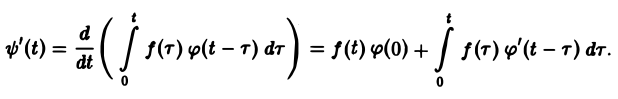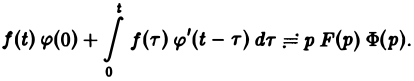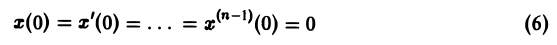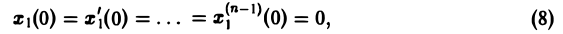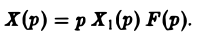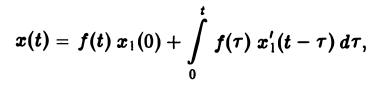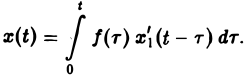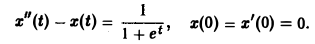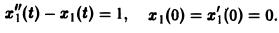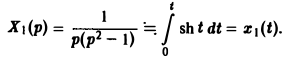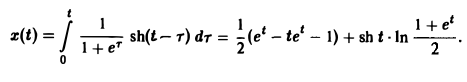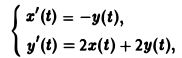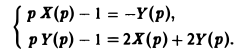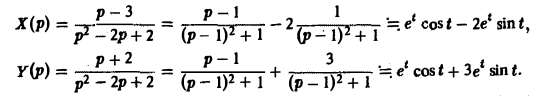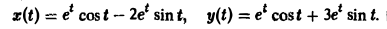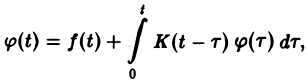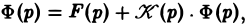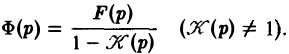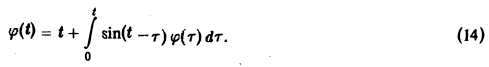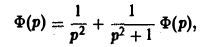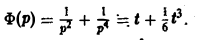Как показать что функция удовлетворяет уравнению лапласа (6 видео)

Преобразование Лапласа с примерами решения и образцами выполнения

Ранее мы рассмотрели интегральное преобразование Фурье

с ядром K(t, ξ) = .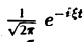

Преобразование Фурье неудобно тем, что должно быть выполнено условие абсолютной интегрируемости функции f(t) на всей оси t,

Преобразование Лапласа позволяет освободиться от этого ограничения.

Определение:

Функцией-оригиналом будем называть всякую комплекснозначную функцию f(t) действительного аргумента t, удовлетворяющую следующим условиям:

f(t) непрерывна на всей оси t, кроме отдельных точек, в которых f(t) имеет разрыв 1-го рода, причем на каждом конечном интервале оси t таких точек может быть лишь конечное число;
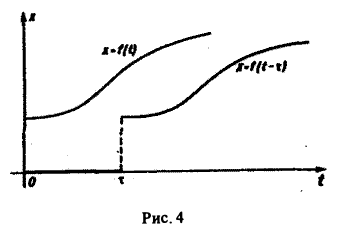
функция f(t) равна нулю при отрицательных значениях t, f(t) = 0 при t 0 и з такие, что для всех t

Ясно, что если неравенство (1) выполняется при некотором s = s1, то оно будет выполнятся при всяком s2 > s1.

Точная нижняя грань sо всех чисел s, so = infs, для которых выполняется неравенство (1), называется показателем роста функции f(t).

Замечание:

В общем случае неравенство

не имеет места, но справедлива оценка

где ε > 0 — любое. Так, функция f(t) = t, t ≥ 0, имеет показатель роста so =0. Для нее неравенство |t| ≤ М ∀t ≥ 0 не выполняется, но ∀ε > О, ∀t > 0 верно неравенство

Условие (1) гораздо менее ограничительное, чем условие (*).

Пример:

не удовлетворяет условию (*), но условие (1) выполнено при любом s ≥ 1 и М ≥ 1; показатель роста so = 1. Так что f(t) является функцией-оригиналом. С другой стороны, функция

не является функцией-оригиналом: она имеет бесконечный порядок роста, sо = +∞. Простейшей функцией-оригиналом является
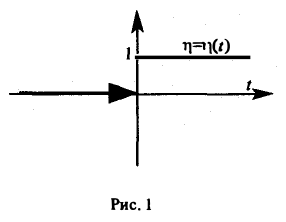
так называемая единичная функция

Если некоторая функция φ(t) удовлетворяет условиям 1 и 3 определения 1, но не удовлетворяет условию 2, то произведение f(t) = φ(t) η(t) уже является функцией-оригиналом.

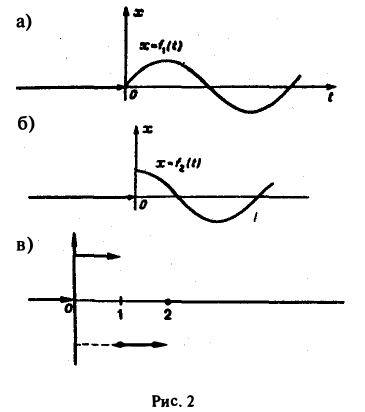
Для простоты записи мы будем, как правило, множитель η(t) опускать, условившись, что все функции, которые мы будем рассматривать, равны нулю для отрицательных t, так что если речь идет о какой-то функции f(t) например, о sin t, cos t, e t и т. д., то всегда подразумеваются следующие функции (рис. 2):

Определение:

Пусть f(t) есть функция-оригинал. Изображением функции f(t) по Лапласу называется функция F(p) комплексного переменного р = s + iσ, определяемая формулой

где интеграл берется по положительной полуоси t. Функцию F(p) называют также преобразованием Лапласа функции f(t); ядро преобразования K(t, р) = e -pt .
Тот факт, что функция f(x) имеет своим изображением F(p), будем записывать так:

Пример:

Найти изображение единичной функции η(t).

Функция 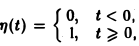является функцией-оригиналом с показателем роста s0 = 0. В силу формулы (2) изображением функции η(t) будет функция

Если р = s + iσ, то при s > 0 интеграл в правой части последнего равенства будет сходящимся, и мы получим

так что изображением функции η(t) будет функция 1/p. Как мы условились, будем писать, что η(t) = 1, и тогда полученный результат запишется так:

Теорема:

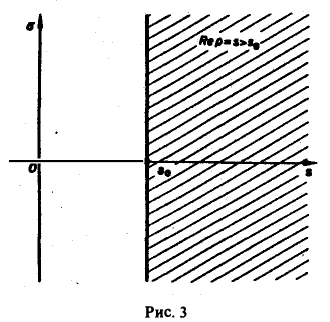
Для всякой функции-оригинала f(t) с показателем роста sо изображение F(p) определено в полуплоскости Re p = s > So и является в этой полуплоскости аналитической функцией (рис. 3).

Для доказательства существования изображения F(p) в указанной полуплоскости достаточно установить, что несобственный интеграл (2) абсолютно сходится при s > so. Используя (3), получаем

что и доказывает абсолютную сходимость интеграла (2). Одновременно мы получили оценку преобразования Лапласа F(p) в полуплоскости сходимости Re р = s > so

Дифференцируя выражение (2) формально под знаком интеграла по р, находим

Существование интеграла (5) устанавливается так же, как было установлено существование интеграла (2).

Применяя для F'(p) интегрирование по частям, получаем оценку

откуда следует абсолютная сходимость интеграла (5). (Внеинтегральное слагаемое 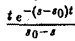— при t → + ∞ имеет предел, равный нулю). В любой полуплоскости Re р ≥ S1 > So интеграл (5) сходится равномерно относительно р, поскольку он мажорируется сходящимся интегралом

не зависящим от р. Следовательно, дифференцированиепо р законно и равенство (5) справедливо.

Поскольку производная F'(p) существует, преобразование Лапласа F(p) всюду в полуплоскости Re p = s > sо является аналитической функцией.

Из неравенства (4) вытекает

Следствие:

Если точка р стремится к бесконечности так, что Re р = s неограниченно возрастает, то

Пример:

Найдем еще изображение функции f(t) =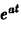, где а = а + iβ — любое комплексное число.

Показатель роста sо функции f(t) равен а.

Считая Rep = s> а, получим

При а = 0 вновь получаем формулу

Обратим внимание на то, что изображение функции 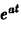является аналитической функцией аргумента р не только в полуплоскости Re p > а, но и во всех точках р, кроме точки р = а, где это изображение имеет простой полюс. В дальнейшем мы не раз встретимся с подобной ситуацией, когда изображение F(p) будет аналитической функцией во всей плоскости комплексного переменного р, за исключением изолированных особых точек. Противоречия с теоремой 1 нет. Последняя утверждает лишь, что в полуплоскости Re p > So функция F(p) не имеет особых точек: все они оказываются лежащими или левее прямой Re p = So, или на самой этой прямой.

Замечание:

В операционном исчислении иногда пользуются изображением функции f(t) по Хевисайду, определяемым равенством

и отличаюикмся от шоСражения по Лапласу множителем р.

Содержание

Свойства преобразования Лапласа
Свертка функций. Теорема умножения
Отыскание оригинала по изображению
Отыскание оригинала с помощью таблиц изображений
Использование теоремы обращения и следствий из нее
Приложения преобразования Лапласа (операционного исчисления)
Решение линейных дифференциальных уравнений с постоянными коэффициентами
Формула Дюамеля
Интегрирование систем линейных дифференциальных уравнений с постоянными коэффициентами
Решение интегральных уравнений
Таблица преобразования Лапласа
Дополнение к преобразованию Лапласа
Электронная библиотека
Преобразование Лапласа
💡 Видео

Видео:показать, что функция удовлетворяет соотношениюСкачать

Свойства преобразования Лапласа

В дальнейшем через f(t), φ(t), … будем обозначать функции-оригиналы, а через F(p), Ф(р), … — их изображения по Лапласу,

Из определения изображения следует, что если f(t) = 9 ∀t, то F(p) = 0.

Теорема единственности:

Теорема:

Справедливость утверждения вытекает из свойства линейности интеграла, определяющего изображение:

— показатели роста функций f(t) и φ(t) соответственно).

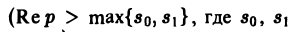
На основании этого свойства получаем

Аналогично находим, что
(4)

Теорема подобия:

Если f(t) — функция-оригинал и F(p) — ее изображение по Лапласу, то для любого постоянного а > 0

Полагая at = т, имеем

Пользуясь этой теоремой, из формул (5) и (6) получаем

Теорема:

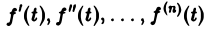
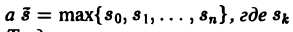
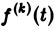
О дифференцировании оригинала. Пусть f(t) является функцией-оригиналом с изображением F(p) и пусть — также функции-оригиналы, — показатель роста функции (k = 0, 1,…, п). Тогда

Здесь под fk(0) (k = 0,1,… , п — 1) понимается правое предельное значение .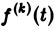

Пусть f(t) = F(p). Найдем изображение f'(t). Имеем

Интегрируя по частям, получаем

Внеинтегральное слагаемое в правой части (10) обращается в нуль при t → + ∞, т. к. при Re р = s > 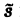имеем

подстановка t = 0 дает -f(0).

Второе слагаемое справа в (10) равно pF(p). Таким образом, соотношение (10) принимаетвид

и формула (8) доказана. В частности, если f(0) = 0, то f'(t) = pF(p). Для отыскания изображения 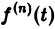запишем

откуда, интегрируя п раз по частям, получим

Пример:

Пользуясь теоремой о дифференцировании оригинала, найти изображение функции f(t) = sin 2 t.

Пусть f(t) = F(p). Тогда

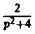
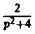
Но f(0) = О, а f'(0) = 2 sin t cos t = sin 2t = . Следовательно, = pF(p), откуда F(p) =

Теорема 5 устанавливает замечательное свойство интегрального преобразования Лапласа: оно (как и преобразование Фурье) переводит операцию дифференцирования в алгебраическую операцию умножения на р.

Формула включения. Если f(t) и f'(t) являются функциями-оригиналами, то (11)

В самом деле, f'(

Так как функция F(p) в полуплоскости Rep = s > so является аналитической, то ее можно дифференцировать по р. Имеем

Последнее как раз и означает, что

Пример:

Пользуясь теоремой 6, найти изображение функции .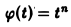

Как известно, 1 = 1/p. Здесь f(t) = 1, F(p) = 1/p. Отсюда (1/p)’= (-t) • 1, или 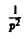= t. Вновь применяя теорему 6, найдем

Теорема:

Интегрирование оригинала. Интегрирование оригинала сводится к делению изображения на р: если f(t) = F(p), то

Нетрудно проверить, что если f(t) есть функция-оригинал, то и φ(t) будет функцией-оригиналом, причем φ(0) = 0. Пусть φ(t) = Ф(р). В силу (14)

С другой стороны, f(t) =’ F(p), откуда F(p) = рФ(р), т.е. Ф(р) =.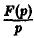

Последнее равносильно доказываемому соотношению (13).

Пример:

Найти изображение функции

В данном случае f(t) = cos t, так что F(p) = 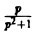. Поэтому

Теорема:

Интегрирование изображения. Если f(t) = F(p) и интеграл 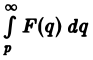сходится, то он служит изображением функции

Предполагая, что путь интегрирования (р, ∞) лежит в полуплоскости Re p ≥ а> so, мы можем изменить порядок интегрирования (t > 0):

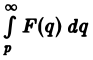
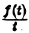
Последнее равенство означает, что является изображением функции .

Пример:

Найти изображение функции .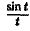

Как известно, sin t = .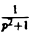

Теорема запаздывания:

Положим ξ = t- τ. Тогда dt = d ξ. При t = τ получаем ξ = 0, при t = + ∞ имеем ξ = + ∞.

Поэтому соотношение (16) принимает вид

Пример:

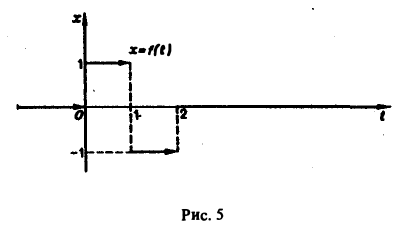
Найти изображение функции f(t), заданной графически (рис. 5).

Запишем выражение для функции f(t) в следующем виде:

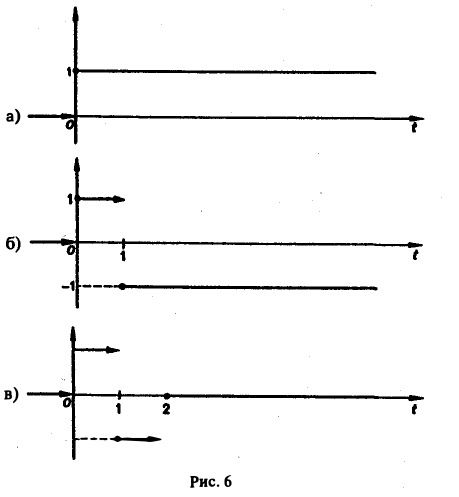
Это выражение можно получить так. Рассмотрим функцию f1(t) = η(t) для t ≥ 0 (рис. 6 а) и вычтем из нее функцию

Разность f(t) — h(t) будет равна единице для t ∈ [0,1) и -1 для t ≥ 1 (рис. 6 b). К полученной разности прибавим функцию

В результате получим функцию f(t) (рис. 6 в), так что

Отсюда, пользуясь теоремой запаздывания, найдем

Теорема смещения:

Теорема позволяет по известным изображениям функций находить изображения тех же функций, умноженных на показательную функцию 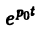, например,

Свертка функций. Теорема умножения

Пусть функции f(t) и φ(t) определены и непрерывны для всех t. Сверткой (f *φ)(t) этих функций называется новая функция от t, определяемая равенством

(если этот интеграл существует).

Для функций-оригиналов f(t) и φ(t) операция свертки всегда выполнима, причем
(17)

В самом деле, произведение функций-оригиналов f( τ ) φ(t — τ), как функция от τ, является финитной функцией, т.е. обращается в нуль вне некоторого конечного промежутка (в данном случае вне отрезка 0 ≤ τ ≤ t). Для финитных непрерывных функций операция свертки выполнима, и мы получаем формулу (17).

Нетрудно проверить, что операциясвертки коммутативна,

Теорема умножения:

Нетрудно проверить, что свертка (f * φ)(t) функций-оригиналов есть функция-оригинал с показателем роста s* = mах, где s1, s2

показатели роста функций f(t) и φ(t) соответственно. Найдем изображение свертки,

Воспользовавшись тем, что

Меняя порядок интегрирования в интеграле справа (при Re р = s > s* такая операция законна) и применяя теорему запаздывания, получим

Таким образом, из (18) и (19) находим

— умножению изображений отвечает свертывание оригиналов,

Пример:

Найти изображение функции

Функция ψ(t) есть свертка функций f(y) = t и φ(t) = sin t. В силу теоремы умножения

Задача:

Пусть функция f(t), периодическая с периодом Т, есть функция-оригинал. Показать, что ее изображение по Лапласу F[p) дается формулой

Видео:Показать, что функция y=e^(-x)sinx удовлетворяет дифференциальному уравнению. Как решать?Скачать

Отыскание оригинала по изображению

Задача ставится так: дана функция F(p), надо найти функцию f(t). изображением которой является F(p).

Сформулируем условия, достаточные для того, чтобы функция F(p) комплексного переменного р служила изображением.

Теорема:

Если аналитическая в полуплоскости Rep = s > so функция F(p)

1) стремится к нулю при |р| —» + ∞ в любой полуплоскости Re р = а > So равномерно относительно arg р;

сходится абсолютно, то F(p) является изображением некоторой функции-оригинала f<t).

Задача:

Может ли функция F(p) = 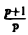служить изображением некоторой функции-оригинала? Укажем некоторые способы отыскания оригинала по изображению.

Отыскание оригинала с помощью таблиц изображений

Прежде всего стоит привести функцию F(p) к более простому, «табличному» виду. Например, в случае, когда F(p) — дробно-рациональная функция аргумента р,ее разлагают на элементарные дроби и пользуются подходящими свойствами преобразования Лапласа.

Пример:

Найти оригинал для

Запишем функцию F(p) в виде:

Пользуясь теоремой смещения и свойством линейности преобразования Лапласа, получаем

Пример:

Найти оригинал для функции

Запишем F(p) в виде

Отсюда f(t) = t — sin t.

Использование теоремы обращения и следствий из нее

Теорема обращения:

где интеграл берется вдоль любой прямой Re p = s > So и понимается в смысле главного значения, т. е. как

Формула (1) называется формулой обращения преобразования Лапласа, или формулой Меллина. В самом деле, пусть, например, f(t) — кусочно-гладкая на каждом конечном отрезке [0, а] функция-оригинал-с показателем роста so. Рассмотрим функцию φ(t) = 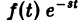, где s>so — любое.

Функция φ(t) удовлетворяет условиям применимости интегральной формулы Фурье, и, следовательно, справедлива формула обращения преобразования Фурье,

(φ(t) ≡ 0 при t

откуда получаем формулу обращения преобразования Лапласа

Как следствие из теоремы обращения получаем теорему единственности.

Теорема:

Две непрерывные функции f(t) и φ(t), имеющие одно и то же изображение F(p), тождественны.
Непосредственное вычисление интеграла обращения (1) обычно затруднительно. Отыскание оригинала по изображению упрощается при некоторых дополнительных ограничениях на F(p).

Теорема:

Пусть изображение F(p) — дробно-рациональная функция с полюсами р1, p2….pп. Тогда оригиналом для F(p) будет функция f(t) η(t), где

Пусть изображение F(p) — дробно-рациональная функция, F(p) = 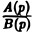, где А(р), В(р) — многочлены относительно р (взаимно простые), причем степень числителя А(р) меньше степени знаменателя В(р), т. к. для всякого изображения должно выполняться предельное соотношение

Пусть корни знаменателя В(р), являющиеся полюсами изображения F(p), суть р1, р2, …, рп, а их кратности равны r1, r2, …, rп соответственно.

Если число s, фигурирующее в формуле (1), взять большим всех Re pk (k = 1,2,…, п), то по формуле обращения, которая в этих условиях применима, получим

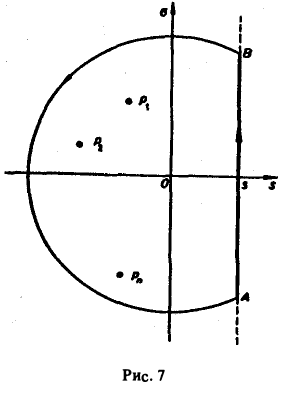
Рассмотрим замкнутый контур ГR (рис.7), состоящий из дуги CR окружности радиуса R с центром в начале координат и стягивающей ее хорды АВ (отрезка прямой Re р = s), и проходимый в положительном направлении, причем радиус R настолько велик, что все полюсы F(p) лежат внутри ГR.

По теореме Коши о вычетах при любом R, удовлетворяющем указанному условию, будем иметь

Второе слагаемое слева в равенстве (5) стремится к нулю при R → ∞. Это следует из леммы Жордана, если в ней заменить р на iz и учесть, что F(p) → 0 при Re p → + ∞. Переходя в равенстве (5) к пределу при R → ∞, мы получим слева

а справа — сумму вычетов по всем полюсам функции F(p)

Замечание:

Воспользовавшись формулой для вычисления вычетов, найдем, что

Если все полюсы p1, р2,…, рn — простые, то

и формула (6) принимает вид

Пример:

Найти оригинал для функции

Функция F(p) имеет простые полюсы р1 = i. p2 = -i. Пользуясь формулой (7), находим

Теорема:

Пусть изображение F(p) является аналитической функцией в бесконечно удаленной точке р = ∞, причем ее разложение в окрестности |р| > R бесконечно удаленной точки имеет вид

Тогда оригиналом для F(p) будет функция f(t) η<t), где

Пример:

Видео:21. Частные производные второго порядка. Часть 4.Скачать

Приложения преобразования Лапласа (операционного исчисления)

Решение линейных дифференциальных уравнений с постоянными коэффициентами

Дано линейное дифференциальное уравнение второго порядка с постоянными коэффициентами
(1)

(ао, а1, а2 — действительные числа) и требуется найти решение уравнения (1) для t > 0, удовлетворяющее начальным условиям

Будем считать, что f(t) есть функция-оригинал. Тогда x(t) — также функция-оригинал. Пусть

f(t) = F(p), x(t) = X(p).

По теореме о дифференцировании оригинала имеем

Перейдем в уравнении (1) от оригиналов к изображениям. Имеем

Это уже не дифференциальное, а алгебраическое уравнение относительно изображения Х(р) искомой функции. Его называют операторным уравнением. Решая его, найдем операторное решение задачи (1)-(2) —

Оригинал для Х(р) будет искомым решением х(t) задачи (1)-(2).

Общий случай линейного дифференциального уравнения n-го порядка (n ≥ 1) с постоянными коэффициентами от случая п = 2 принципиально ничем не отличается.

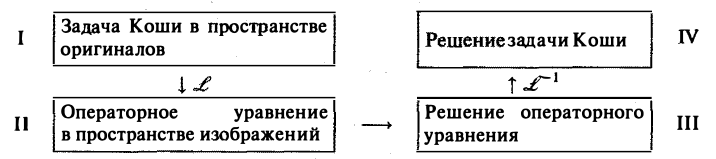
Приведем общую схему решения задачи Коши

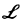
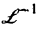
Здесь означает применение к 1 преобразование Лапласа, — применение к III обратного преобразования Лапласа.

Пример:

Решить задачу Коши

По теореме о дифференцировании изображения

Формула Дюамеля

В приложениях операционного исчисления к решению дифференциальных уравнений часто пользуются следствием из теоремы умножения, известным под названием формулы Дюамеля.

Пусть f(t) и φt) — функции-оригиналы, причем функция f(t) непрерывна на [0, + ∞), a φ(t) — непрерывно дифференцируема на [0,+ ∞). Тогда если f(t) = F(p), φ<t) = Ф(р),то по теореме умножения получаем, что

Нетрудно проверить, что функция ψ(t) непрерывно дифференцируема на [0, + ∞), причем

Отсюда, в силу правила дифференцирования оригиналов, учитывая, что ψ(0) = 0, получаем формулу Дюамеля
(4)

Покажем применение этой формулы.

Пусть требуется решить линейное дифференциальное уравнение n-го порядка (n ≥ 1) с постоянными коэффициентами

при нулевых начальных условиях

(последнее ограничение несущественно: задачу с ненулевыми начальными условиями можно свести к задаче с нулевыми условиями заменой искомой функции).

Если известно решение x(t) дифференциального уравнения с той же левой частью и правой частью, равной единице,

L[x(t)] = l (7)

при нулевых начальных условиях

то формула Дюамеля (4) позволяет сразу получить решение исходной задачи (5)-(6).

В самом деле, операторные уравнения, отвечающие задачам (5)-(6) и (7)-(8), имеют соответственно вид

где F(p) — изображение функции f(t). Из (9) и (10) легко находи

Отсюда по формуле Дюамеля

или, поскольку x1(0) = 0, (11)

Пример:

Решить задачу Коши

Рассмотрим вспомогательную задачу

Применяя операционный метод, находим

По формуле (11) получаем решение x(t) исходной задачи:

Интегрирование систем линейных дифференциальных уравнений с постоянными коэффициентами

Интегрирование систем осуществляется так же, как и решение одного линейного дифференциального уравнения — путем перехода от системы дифференциальных уравнений к системе операторных уравнений. Решая последнюю как систему линейных алгебраических уравнений относительно изображений искомых функций, получаем операторное решение системы. Оригинал для негобудетрешением исходной системы дифференциальных уравнений.

Пример:

Найти решение линейной системы

удовлетворяющее начальным условиям х(0) = у(0) = I.

Пусть х(

Решая последнюю относительно Х(р) и У(р), получаем

Решение исходной задачи Коши

Решение интегральных уравнений

Напомним, что интегральным уравнением называют уравнение, в котором неизвестная функция входит под знак интеграла. Мы рассмотрим лишь уравнение вида (12)

называемое линейным интегральным уравнением Вольтерра второго рода с ядром K(t — т), зависящим от разности аргументов (уравнение типа свертки). Здесь φ(t) — искомая функция, f(t) и K(t) — заданные функции.

Пусть f(t) и K(t) есть функции-оригиналы, f(t) =’ F(p), K(t) =’ K(p).

Применяя к обеим частям (12) преобразование Лапласа и, пользуясь теоремой умножения, получим
(13)

где Ф(р) = φ(t). Из (13)

Оригинал для Ф(р) будет решением интегрального уравнения (12).

Пример:

Решить интегральное уравнение

Применяя преобразование Лапласа к обеим частям (14), получим

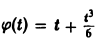
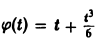
Функция является решением уравнения (14) (подстановка в уравнение (14) обращает последнее в тождество по t).

Замечание:

Преобразование Лапласа может быть использовано также при решении некоторых задач для уравнений математической физики.

Видео:Частные производные функции многих переменныхСкачать

Таблица преобразования Лапласа

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Дополнение к преобразованию Лапласа

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

Видео:7.1 Решение уравнения Лапласа в прямоугольникеСкачать

Электронная библиотека

Пусть имеется однородное тело V, ограниченное поверхностью S. Как известно, температура тела удовлетворяет уравнению:

Если процесс установившийся (стационарный), т.е. u(x,y,z) не зависит от времени, то . Следовательно, температура u(x,y,z) удовлетворяет уравнению Лапласа:

Функции u, удовлетворяющие уравнению Лапласа называются гармоническими (см. главу 2).

Чтобы температура в теле определялась однозначно из уравнения Лапласа, нужно знать температуру на поверхности S. Таким образом, для уравнения Лапласа краевая задача формулируется так: найти функцию u(x,y,z), удовлетворяющую уравнению (4.71) внутри объема V и принимающую в каждой точке заданные значения:

Эта задача называется задачей Дирихле или первой краевой задачей для уравнения Лапласа (4.71).

Если рассматривать плоский случай, то уравнению Лапласа должна удовлетворять функция u(x,y), а краевые условия должны иметь место на контуре С, ограничивающем односвязную область D плоскости хОу.

Замечание. В практике часто пользуются уравнением Лапласа, записанного в цилиндрических координатах (полярных, если случай плоский).

Если ввести в рассмотрение цилиндрические координаты: , то заменяя x, y, z на r, , z, приходят к функции и * ( r, , z), а уравнение Лапласа этой функции будет иметь вид:

Если функция u не зависит от z, а зависит только от х и у, то функция и * =и * ( r, ) и удовлетворяет уравнению Лапласа:

Найдём решение задачи Дирихле для круга. Пусть в плоскости Х0У задан круг радиусом R с центром в начале координат и на его окружности задана функция , где – полярный угол. Требуется найти функцию и( r, ), непрерывную в круге, включая границу, удовлетворяющую внутри круга уравнению Лапласа:

и на окружности круга принимающую заданные значения:

Задачу решаем в полярных координатах. Тогда уравнение (4.75) будет:

Решение ищем методом разделения переменных, полагая

Подставляя в уравнение Лапласа, приходим:

Последнее равенство дает два уравнения:

Общее решение уравнения (4.80) будет:

Общее решение уравнения (4.81):

(решение ищется в форме ).

Запишем решение в виде:

Если k = 0, то должны взять (решение должно быть периодической функцией).

Как и ранее решение задачи получим, суммируя все u_k в (4.84), а следовательно, сумма должна быть периодической функцией от , Для этого k должно принимать целые значения (в самом начале мы взяли , а не , так как числу не отвечало бы периодическим решениям). Функция ограниченна только положительными значениями k = 1, 2,…,n,…, так как в силу произвольности A, B, C, D отрицательные значения k новых частных решений не дают.

Подставив в равенство (4.85) r = R, получим:

Отсюда видно, что функция должна разлагаться в ряд Фурье в интервале и , должны быть коэффициентами Фурье. Следовательно,

Подставляя в формулу (4.85) значения А_n и В_n из (4.87) и проведя тождественные преобразования (рекомендуется выполнить самостоятельно в качестве упражнения), получим:

Формула (4.88) называется интегралом Пуассона. Этим и завершается решение задачи Дирихле для круга.

Показать, что функция есть гармоническая функция.

Решение. По определению функция u(x,y) называется гармонической в некоторой области, если в каждой точке этой области она удовлетворяет уравнению Лапласа:

Вывод: функция гармоническая.

Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00

Видео:Дифференциальные уравнения, 1 урок, Дифференциальные уравнения. Основные понятияСкачать

Преобразование Лапласа

По этой ссылке вы найдёте полный курс лекций по математике:

рассмотрели интегральное преобразование Фурье с ядром K(t, О = е Преобразование Фурье неудобно тем, что должно быть выполнено условие абсолютной интегрируемости функции f(t) на всей оси t, Преобразование Лапласа позволяет освободиться от этого ограничения. Определение 1. Функцией-оригиналом будем называтьвсякую комплекснозначную функцию f(t) действитсл ьного аргумента t, удовлетворя юшую следующим условиям:

1. f(t) непрерывна на всей оси t, кроме отдельных точек, в которых f(t) имеет разрыв 1-го рода, причем накаждом конечном интервалеоси *такихточек можетбыть лишь конечное число; 2. функция f(t) равна нулю при отрицательных значениях t, f(t) = 0 при 3. при возрастании t модуль f(t) возрастает не быстрее показательной функции, т. е. существуют числа М > 0 и s такие, что для всех t Ясно, что если неравенство (1) выполняется при некотором s = aj, то оно будет ВЫПОЛНЯТЬСЯ и при ВСЯКОМ 82 > 8].

Точная нижняя грань s0 всех чисел з, «о = infs, для которых выполняется неравенство (1), называется показателем роста функции f(t). Замечание. В общем случае неравенство не имеет места, но справедлива оценка где е > 0 — любое. Так, функция имеет показатель роста в0 = Для нее неравенство t ^ М V* ^ 0 не выполняется, но верно неравенство |f| ^ Меи. Условие (1) гораздо менее ограничительное, чем условие (*). Пример 1. функция не удовлетворяет условию (»), но условие (1) выполнено при любом s ^ I и А/ ^ I; показатель роста 5о = • •

Так что является функцией-оригиналом. С другой стороны, функция не является функцией-оригиналом: она имеет бесконечный порядок роста, «о = +оо. Простейшей функцией-оригиналом является так называемая единичная функция Если некоторая функция удовлетворяет условиям 1 и 3 определения 1, но не удовлетворяет условию 2, то произведение уже является функцией-оригиналом.

Для простоты записи мы будем, как правило, множитель rj(t) опускать, условившись, что все функции, которые мы будем рассматривать, равны нулю для отрицательных t, так что если речь идет о какой-то функции f(t), например, о sin ty cos t, el и т. д., то всегда подразумеваются следующие функции (рис. 2): п=п(0 Рис. 1 Определение 2. Пусть f<t) есть функция-оригинал. Изображением функции f(t) по Лапласу называется функция F(p) комплексного переменного , определяемая формулой ПРЕОБРАЗОВАНИЕ ЛАПЛАСА Основные определения

Свойства Свертка функций Теорема умножения Отыскание оригинала по изображению Использование теоремы обращения операционного исчисления Формула Дюамеля Интегрирование систем линейных дифференциальных уравнений с постоянными коэффициентами Решение интегральных уравнений где интеграл берется по положительной полуоси t. Функцию F(p) называют также преобразованием Лапласа функции /(/); ядро преобразования K(t> р) = e

pt. Тот факт, что функция имеет своим изображением F(p), будем записывать Пример 2. Найти изображение единичной функции r)(t).

Возможно вам будут полезны данные страницы:

Функция является функцией-оригиналом с показателем роста в0 — 0. В силу формулы (2) изображением функции rj(t) будет функция Если то при интеграл в правой части последнего равенства будет сходящимся, и мы получим так что изображением функции rj(t) будет функция £. Как мы условились, будем писать, что rj(t) = 1, и тогда полученный результат запишется так: Теорема 1. Лгя всякой функции-оригинала f(t) с показателем роста з0 изображение F(p) определено в полуплоскости R ер = s > s0 и является в этой полуплоскости аналитической функцией (рис. 3).

Пусть Для доказательства существования изображения F(p) в указанной полуплоскости достаточно установить, что несобственный интеграл (2) абсолютно сходится при a > Используя (3), получаем что и доказывает абсолютную сходимость интеграла (2). Одновременно мы получили оценку преобразования Лапласа F(p) в полуплоскости сходимости Дифференцируя выражение (2) формально под знаком интеграла по р, находим Существование интеграла (5) устанавливается так же, как было установлено существование интеграла (2).

Применяя для F'(p) интегрирование по частям, получаем оценку откуда следует абсолютная сходимость интеграла (5). (Внеинтегральное слагаемое ,0.,— при t +оо имеет предел, равный нулю). В любой полуплоскости Rep ^ sj > «о интеграл (5) сходится равномерно относительно р, поскольку он мажорируется сходящимся интегралом не зависящим от р. Следовательно, дифференцированиепо р законно и равенство (5) справедливо. Поскольку производная F'(p) существует, преобразование Лапласа F(p) всюду в полуплоскости Rep = 5 > 5о является аналитической функцией. Из неравенства (4) вытекает Следствие.

Если тонка р стремится к бесконечности так, что Re р = s неограниченно возрастает, то Пример 3. Найдем еще изображение функции любое комплексное число. Показатель росга «о функции /(() равен а. 4 Считая Rep = я > а, получим Таким образом, При а = 0 вновь получаем формулу Обратим внимание на то, что изображение функции eat является аналитической функцией ар1умента р не только в полуплоскости Rep > а, но и во всех точках р, кроме точки р = а, где это изображение имеет простой полюс.

В дальнейшем мы не раз встретимся с подобной ситуацией, когда изображение F(p) будет аналитической функцией во всей плоскости комплексного переменного р, за исключением изолированных особых точек. Противоречия с теоремой 1 нет. Последняя утверждает лишь, что в полуплоскости Rep > «о функция F(p) не имеет особых точек: все они оказываются лежащими или левее прямой Rep = so, или на самой этой прямой. Замечай не. В операционном исчислении иногда пользуются изображением функции /(f) по Хевисайду, определяемым равенством и отличающимся от мображения по Лапласу множителем р. §2.

Свойства преобразования Лапласа В дальнейшем через будем обозначать функции-оригиналы, а через — их изображения по Лапласу, Из определения изображения следует, что если Теорема 2 (единстве* мости ). £biw dee непрерывные функции ) имеют одно и тоже изображение , то они тождественно равны. Teopewa 3 (п«иейиост* преобраэдоияя Лапласа). Если функции-оригиналы, то для любых комплексных постоянных аир Справедливость утверждения вытекает из свойства линейности интеграла, определяющего изображение: , — показатели роста функций соответственно).

На основании этогосвойства получаем Аналогично находим, что и, далее, Теорема 4 (подобия). Если f(t) — функция-оригинал и F(p) — ее изображение по Лапласу, то для любого постоянного а > О Полагая at = т, имеем Пользуясь этой теоремой, из формул (5) и (6) получаем Теорема 5 (о дифференцировании оригинала). Пусть является функцией-оригиналом с изображением F(p) и пусть — также функции-оригиналы, а где — показатель роста функции Тогда и вообще Здесь под понимается правое предельное значение Пусть .

Пусть Следовательно, Теорема 5 устанавливает замечательное свойство интегрального преобразования Лапласа: оно (как и преобразование Фурье) переводит операцию дифференцирования в алгебраическую операцию умножения на р. Формула включения. Если являются функциями-оригиналами, то В самом деле, В силу следствия из теоремы 1, всякое изображение стремится к нулю при . Значит, , откуда вытекает формула включения ( Теорема 6 (о дифференцировании изображения).

Дифференцирование изображения сводится к умножению на оригинала, Так как функция F(p) в полуплоскости so является аналитической, то ее можно дифференцировать по р. Имеем Последнее как раз и означает, что Пример 5. Пользуясь теоремой 6, найти изображение функции 4 Как известно, Отсюда ( Вновь применяя теорему 6, найдем , вообще Теорема 7 (интегрирование оригинала). Интегрирование оригинала сводится к делению изображения на Положим Нетрудно проверить, что если есть функция-оригинал, то и будет функцией-оригиналом, причем .

Пусть . В силу так что С другой стороны, , откуда F= Последнее равносильно доказываемому соотношению (13). Пример 6. Найти изображение функции M В данном случае , так что . Поэтому Теорема 8 (интегрирование изображения). Если и интеграл сходится, то он служит изображением функции ^:

ПРЕОБРАЗОВАНИЕ ЛАПЛАСА Основные определения Свойства Свертка функций Теорема умножения Отыскание оригинала по изображению Использование теоремы обращения операционного исчисления Формула Дюамеля Интегрирование систем линейных дифференциальных уравнений с постоянными коэффициентами Решение интегральных уравнений Действительно, Предполагая, что путь интегрирования лежите полуплоскости so, мы можем изменить порядок интегрирования Последнее равенство означает, что является изображением функции Пример 7. Найти изображение функции М Как известно, .

Поэтому Так как Положим получаем £ = 0, при. Поэтому соотношение (16) принимает вид Примере. Найти изображение функции f(t), заданной графически (рис.5). Запишем выражение для функции f(t) в следующем виде: Это выражение можно получить так. Рассмотрим функцию и вычтем из нее функцию Разность будет равна единице для . К полученной разности прибавим функцию В результате получим функцию f(t) (рис. 6 в), так что Отсюда, пользуясь теоремой запаздывания, найдем Теорема 10 (смещения). то для любого комплексного числа ро.

В самом деле, Теорема позволяет по известным изображениям функций находить изображения тех же функций, умноженных на показательную функцию , например, 2.1.

Свертка функций. Теорема умножения Пусть функции /(£) и определены и непрерывны для всех t. Сверткой этих функций называется новая функция от t, определяемая равенством (если этот интеграл существует). Для функций-оригиналов операция свертим всегда выполнима, причем (17) 4 В самом деле, произведение функций-оригиналов как функция от т, является финитной функцией, т.е. обращается в нуль вне некоторого конечного промежутка (в данном случае вне отрезка .

Для финитных непрерывных функций операция свертки выполнима, и мы получаем формулу Нетрудно проверить, что операциясвертки коммутативна, Теорема 11 (умножения). Если , то свертка t) имеет изображение Нетрудно проверить, что свертка ( функций-оригиналов есть функция-оригинал с показателем роста » где , — показатели роста функций соответственно. Найдем изображение свертки, Воспользовавшись тем, что будем иметь Меняя порядок интегрирования в интеграле справа ( такая операция законна) и применяя теорему запаздывания, получим.

Таким образом, из (18) и (19) находим — умножению изображений отвечает свертывание оригиналов, Пртер 9. Найти изображение функции А функция V(0 ость свортка функций . В силу теоремы умножения Задача. Пусть функция /(£), пориодическая с периодом Т, есгъ функция-оригинал. Показать, что ее изображение по Лапласу F(p) дается формулой 3. Отыскание оригинала по изображению Задача ставится так: дана функция F(p), надо найти функцию /( изображением которой является F(p). Сформулируем условия, достаточные для того, чтобы функция F(p) комплексного переменного р служила изображением.

Теорема 12. Если аналитическая в полуплоскости so функция F(p) 1) стремится к нулю при в любой полуплоскости R s0 равномерно относительно arg р; 2) интеграл сходится абсолютно, то F(p) является изображением некоторой функции-оригинала Задача. Может ли функция F(p) = служить изображением некоторой функции-оригинала? Укажем некоторые способы отыскания оригинала по изображению. 3.1. Отыскание оригинала с помощью таблиц изображений Прежде всего стоит привести функцию F(p) к более простому, «табличному» виду.

Например, в случае, когда F(p) — дробно-рациональная функция аргумента р,ее разлагают на элементарные дроби и пользуются подходящими свойствами преобразования Лапласа. Пример 1. Найти оригинал для Запишем функцию F<p) в виде Пользуясь теоремой смещения и свойством линейности преобразования Лапласа, получаем Пример 2. Найти оригинал для функции 4 Запишем F(p) в виде Отсюда 3.2.

Использование теоремы обращения и следствий из нее Теорема 13 (обращения). Если функция fit) есть функция-оригинал с показателем роста s0 и F(p) — ее изображение, то в любой точке непрерывности функции f(t) выполняется соотношение где интеграл берется вдоль любой прямой и понимается в смысле главного значения, т. е. как Формула (1) называется формулой обращения преобразования Лапласа, или формулой Меллина.

В самом деле, пусть, например, f(t) — кусочно-гладкая на каждом конечном отрезке [0, а) функция-оригинал-с показателем роста s0. Рассмотрим функцию любое. Функция удовлетворяет условиям применимости интегральной формулы Фурье, и, следовательно, справедлива формула обращения преобразования Фурье, Подставляя в (3) выражение найдем где F(p) — преобразование Лапласа функции f(t) при р = 8 + Формулу (2) можно переписать в виде откуда получаем формулу обращения преобразования Лапласа Как следствие из теоремы обращения получаем теорему единственности.

Теорема 14. Две непрерывные функции , имеющие одно и то же изображение F(p), тождественны. Непосредственное вычисление интеграла обращения (1) обычно затруднительно. Отыскание оригинала по изображению упрощается при некоторых дополнительных ограничениях на F(p). Теорема 15. Пусть изображение F(p) — дробно-рациональная функция с пмюсами Рп-

Тогда оригиналом для F(p) будет функция , где Пусть изображение F(p) — дробно-рациональная функция, многочлены относительно р (взаимно простые), причем степень числителя А(р) меньше степени знаменателя В(р), т.к. для всякого изображения должно выполняться предельное соотношение Пусть корни знаменателя В(р), являющиеся полюсами изображения а их кратности равны тп соответственно.

Если число 5, фигурирующее в формуле (1), взять большим всех то по формуле обращения, которая в этих условиях применима, получим Рассмотрим замкнутый контур Гд (рис.7), состоящий из дуги CR окружности радиуса R с центром в начале координат и стягивающей ее хорды АВ (отрезка прямой Re р = з), и проходимый в положительном направлении, причем радиус R настолько велик, что все полюсы F(p) лежат внутри Гл. По теореме Коши о вычетах при любом R, удовлетворяющем указанному условию, будем иметь Второе слагаемое слева в равенстве (5) стремится к нулю при R оо.

Это следует из леммы Жордана

если в ней заменить р на iz и учесть, что F(p) 0 при Rep +оо. Переходя в равенстве (5) к пределу при R-* оо, мы получим слева а справа,— сумму вычетов по всем полюсам функции F(p) ПРЕОБРАЗОВАНИЕ ЛАПЛАСА Основные определения Свойства Свертка функций Теорема умножения Отыскание оригинала по изображению Использование теоремы обращения операционного исчисления Формула Дюамеля Интегрирование систем линейных дифференциальных уравнений с постоянными коэффициентами Решение интегральных уравнений Замечание.

Воспользовавшись формулой для вычисления вычетов, найдем, что Если все полюсы р, рз. рп — просгые, то и формула (6) принимает вид Пример 3. Найти оригинал для функции Теорема 16. Пусть изображение F(p) является аналитической функцией в бесконечно удаленной точке р = оо, причем ее раз,южение в окрестности > R бесконечно удаленной точки имеет вид Тогда оригиначом для F<p) будет функция , где § 4. Приложения преобразования Лапласа (операционного исчисления) 4.1.

Решение линейных дифференциальных уравнений с постоянными коэффициентами Дано линейное дифференциальное уравнение второго порядка с постоянными коэффициентами действительные числа) и требуется найти решение x(t) уравнения (1) для t > 0, удовлетворяющее начальным условиям Будем считать, что f(t) есть функция-оригинал. Тогда x(t) — также функция-оригинал. Пусть По теореме о дифференцировании оригинала имеем ,.

Перейдем в уравнении (1) от оригиналов к изображениям. Имеем Это уже не дифференциальное, а алгебраическое уравнение относительно изображения Х(р) искомой функции. Его называют операторным уравнением. Решая его, найдем операторное решение задачи (1)-(2) — Оригинал для Х(р) будет искомым решением x(t) задачи (1)-(2). Обший случай линейного дифференциального уравнения n-го порядка (n ^ 1) с постоянными коэффициентами от случая п = 2 принципиально ничем не отличается.

Приведем общую схему решения задачи Коши Х(р) = Задача Коши в пространстве оригиналов IV I Решение задачи Коши Т-Г’ Операторное уравнение в пространстве изображений Решение операторного уравнения III II Здесь Л означает применение к 1 преобразование Лапласа, JT1 — применение к III обратного преобразования Лапласа. Пример 1. Решить задачу Коши I. Операторное уравнение откуда По теореме о дифференцировании изображения Поэтому Формула Дюамеля В приложениях операционного исчисления к решению дифференциальных уравнений часто пользуются следствием из теоремы умножения, известным под названием формулы Дюамеля.

Пусть — функции-оригиналы, причем функция f(t) непрерывна на непрерывно дифференцируема на Тогда если ,то потеоремеумножения получаем, что Нетрудно проверить, что функция ip(t) непрерывно дифференцируема на причем Отсюда, в силу правила дифференцирования оригиналов, учитывая, что , получаем формулу Дюамеля (4) Покажем применение этой формулы. Пусть требуется решить линейное дифференциальное уравнение n-го порядка (n ^ 1) с постоянными коэффициентами при нулевых начальных условиях (последнее ограничение несущественно: задачу с ненулевыми начальными условиями можно свести к задаче с нулевыми условиями заменой искомой функции).

Если известно решение Х (t) дифференциального уравнения с той же левой частью и правой частью, равной единице, при нулевых начальных условиях то формула Дюамеля (4) позволяет сразу получить решение исходной задачи В самом деле, операторные уравнения, отвечающие задачам ), имеют соответственно вид и где F(p) — изображение функции ) легко находим Отсюда по формуле Дюамеля t или, поскольку Пример 2.

Решить задачу Коши Рассмотрим вспомогательную задачу Применяя операционный метод, находим По формуле (П) получаем решение x(t) исходной задачи: ПРЕОБРАЗОВАНИЕ ЛАПЛАСА Основные определения Свойства Свертка функций Теорема умножения Отыскание оригинала по изображению Использование теоремы обращения операционного исчисления Формула Дюамеля Интегрирование систем линейных дифференциальных уравнений с постоянными коэффициентами Решение интегральных уравнений 4.2.

Интегрирование систем линейных дифференциальных уравнений с постоянными коэффициентами Интегрирование систем осуществляется так же, как и решение одного линейного дифференциального уравнения — путем перехода от системы дифференциальных уравнений к системе операторных уравнений. Решая последнюю как систему линейных алгебраических уравнений относительно изображений искомых функций, получаем операторное решение системы.

Оригинал для него будет решением исходной системы дифференциальных уравнений. Пример 3. Найти решение линейной системы удовлетворяющее начальным условиям 4 Пусть Пользуясь свойством линейности преобразования Лапласа и теоремой о дифференцировании оригиналов, сводим исходную задачу Коши к операторной системе Решение исходной задачи Коши 4.3. Решение интегральных уравнений Напомним, что интегральным уравнением называют уравнение, в котором неизвестная функция входит под знак интеграла.

Мы рассмотрим лишь уравнение вида (12) называемое линейным интегральным уравнением Вольтерра второго рода с ядром зависящим от разности аргументов (уравнение типа свертки). Здесь — искомая фуннция, — заданные функции. Пусть f(t) и K(t) есть функции-оригиналы, . Применяя к обеим частям (12) преобразование Лапласа и, пользуясь теоремой умножения, получим Решая последнюю относительно, получаем Оригинал для Ф(р) будет решением интегрального уравнения (12).

Пример 4. Решить интегральное уравнение 4 Применяя преобразование Лапласа к обеим частям (14), получим Функция является решением уравнения (14) (подстановка уравнение (14) обращает поело дне© в тождество Замечание. Преобразование Лапласа может быть использовано также при решении некоторьж задач для уравнений математической физики. Функция-оригинал Преобразование Лапласа Упражнения Установите, каше из указанных функций являются функциями-оригиналами:

Пользуясь свойствами преобразования Лапласа, найдите изображения следующих функций: Найдите изображение следующих функций, заданных графически: Найдите оригиналы по заданному изображению: Решите задачу Коши для следующих дифференциальных уравнений: Решите задачу Коши доя следующих систем дифференциальных уравнений: Решите интегральные уравнения:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.