Как по дифференциальному уравнению звена найти его передаточную функцию (5 видео)

Переход от передаточной функции к дифференциальному уравнению

Очевидно, что в обратном порядке можно от передаточной функции перейти к дифференциальному уравнению. Для этого нужно приравнять передаточную функцию, согласно ее определению, отношению изображения выхода к изображению входа, перейти к записи уравнения для изображений в строчку (П6.3.1) и затем от него перейти к уравнению для оригиналов (П6.1.1) или (П6.1.3).

Например, найдем дифференциальное уравнение для передаточной функции колебательного звена с передаточной функцией:

Для этого приравняем передаточную функцию отношению изображений Y(p)/X(p) и перепишем уравнение в строчку:

Теперь перейдем к оригиналам при нулевых начальных условиях. Формально заменим изображения Y(p), Х(р) на оригиналы y(t), x(t)

и переменную Лапласа р = а + ja — на оператор дифференцирова- d

ния р =—: dt

или в классической форме:

Дифференциальному уравнению соответствует характеристический полином

совпадающий с знаменателем передаточной функции. Чтобы записать характеристический полином или характеристическое уравнение по дифференциальному уравнению, надо в его левой части заменить производные соответствующими степенями переменной, причем y(t) заменяется на р° = 1.

Содержание

Типовые звенья систем автоматического регулирования
Как по дифференциальному уравнению звена найти его передаточную функцию
Как по дифференциальному уравнению звена найти его передаточную функцию
W n ( p )
W ос ( p )
📽️ Видео

Видео:Видеометодичка. Практикум по нахождению передаточных функций по дифференциальным уравнениямСкачать

Типовые звенья систем автоматического регулирования

По виду передаточной функции или дифференциального уравнения различают следующие звенья [4, 79, 82]:

1. Усилительное (безынерционное):

Размерность коэффициента усиления к определяется размерностями входной и выходной величины. В любом случае (к > 1 или к 0, а инверсию сигнала будем учитывать инвертирующим звеном с передаточной функцией W(p) = —1.

2. Идеальное интегрирующее:

Размерность коэффициента усиления [_с— 1 ], а постоянной времени

3. Идеальное дифференцирующее:

4. Инерционное (апериоди ческое I порядка):

Размерности коэффициента усиления и постоянной времени ано- логичны размерностям в предыдущих звеньях.

Частота сопряжения со₀ = |^с -1 J определяет полосу пропускания

Здесь ?, — коэффициент затухания (демпфирования); со₀ — чд- стота сопряжения.

Корни характеристического уравнения р_х2 =-^со₀ ± у’со₀ yjl-Z, 2 являются комплексно-сопряженными, что определяет колебательный характер переходного процесса. Отсюда и название звена.

Звено является частным случаем колебательного при % = 0.

В дифференциальном уравнении отсутствует член с первой производной, сответствующий вязкому трению и, следовательно, рассеиванию энергии. Примером консервативного звена является математический маятник (без трения и сопротивления воздуха). Выведенный из состояния равновесия маятник совершает незатухающие колебания. При этом кинетическая энергия переходит в потенциальную и обратно, а сумма энергий остается постоянной величиной.

Видео:7) ТАУ для чайников.Части 3.4 и 3.5 : Передаточная функция. Преобразование Лапласа...Скачать

Как по дифференциальному уравнению звена найти его передаточную функцию

Понятие линейного динамического звена

САУ удобно представлять для анализа и при синтезе в виде взаимосвязанной совокупности отдельных элементов динамических звеньев.

Под динамическим звеном понимают в общем случае абстрактное устройство, имеющее вход и выход, и для которого задано уравнение, связывающее сигналы на входе и выходе, как это показано на рис. 1.

Подробное изучение свойств реальных объектов управления и систем автоматического управления приводит к описанию динамических звеньев в виде нелинейных дифференциальных уравнений. Но во многих случаях их можно линеаризовать, то есть заменить нелинейные уравнения линейными, приближенно описывающими процессы в системах. Тем самым осуществляется декомпозиция задач анализа и синтеза систем, то есть первоначально используют линейное представление, а затем осуществляют учет вносимых нелинейностями особенностей. Такому подходу способствует то, что, в большинстве случаев, нормально функционирующая система работает в режиме малых отклонений, при которых нелинейности не проявляются. В дальнейшем мы будем рассматривать преимущественно аппарат изучения линейных систем, а особенности систем других классов: нелинейных, импульсных, цифровых и стохастических, будут излагаться позднее в других учебных дисциплинах.

Если уравнение, связывающее сигналы и , линейно, то говорят о линейном динамическом звене

Уравнение линейного динамического звена имеет следующий общий вид:

где — постоянные коэффициенты, .

Использовать такое описание динамического звена в задачах анализа и синтеза систем и объектов управления не рационально, поэтому существуют и иные формы описания и представления динамических звеньев и систем в целом.

Подвергнем уравнение (1) преобразованию Лапласа, считая начальные условия нулевыми и заменяя оригиналы сигналов их изображениями по Лапласу

Используя теоремы преобразования Лапласа линейности и дифференцирования, получим операторное уравнение, связывающие изображения входного и выходного сигналов

Преобразуем уравнение (2) к следующему виду

Получим из (3) отношение изображений выходного и входного сигналов

Отношение (4) не зависит от изображений сигналов, определяется только параметрами самого динамического звена (), имеет вид дробно-рациональной функции.

Отношение изображений выходного и входного сигналов называют передаточной функцией динамического звена

называют характеристическим уравнением динамического звена, так как знаменатель передаточной функции это характеристический полином дифференциального уравнения, описывающего динамическое звено.

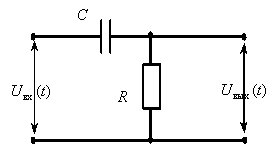
Определим передаточную функцию динамического звена по его принципиальной электрической схеме

По второму закону Кирхгоффа запишем уравнения описывающие схему

С учетом того, что

Получим операторные уравнения

Из второго уравнения выразим значение изображения тока

Подставим полученное выражение в первое уравнение системы

В итоге получаем искомую передаточную функцию

Графически передаточные функции динамического звена представляют в следующем виде:

Если известно изображение входного сигнала и передаточная функция динамического звена, всегда можно найти изображение выходного сигнала при нулевых начальных условиях

.(5)

В общем случае САУ состоит из множества динамических звеньев, сигналы с выходов звеньев могут суммироваться или вычитаться, суммироваться с внешними для САУ сигналами. Суммирование и вычитание изображений сигналов могут быть представлено графически с помощью суммирующих звеньев:

Показанная выше неоднозначность графического представления вычитания изображений на суммирующем элементе связана с различием в стандартах разных стран.

Используя графическое представление передаточных функций звеньев и суммирующие звенья, можно в графической форме представить операторные уравнения, описывающие САУ. Такое графическое представление операторных уравнений в ТАУ называют структурной схемой.

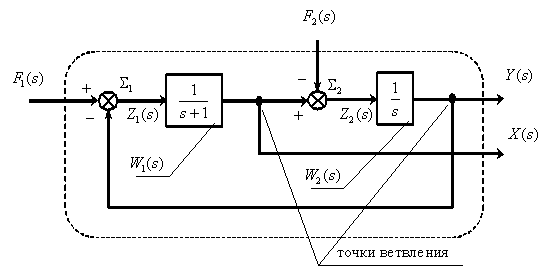
По математической модели объекта управления в форме системы дифференциальных уравнений определить структурную схему объекта.

Получим систему операторных уравнений, подвергнув исходную систему дифференциальных уравнений преобразованию Лапласа и заменив оригиналы изображениями,

Из первого уравнения системы операторных уравнений, которое описывает динамическое звено объекта управления, после преобразований получим

Тогда передаточная функция этого звена имеет вид

а выражение описывает суммирующее звено . Таким образом, получены два фрагмента структурной схемы

Из второго уравнения системы операторных уравнений, которое описывает динамическое звено объекта управления, после преобразований получим, вводя обозначение,

Тогда передаточная функция этого звена имеет вид

а выражение описывает суммирующее звено . Таким образом, получены еще два фрагмента структурной схемы

Соединим все фрагменты структурной схемы объекта управления, объединяя одноименные сигналы, либо разветвляя их с помощью точек ветвления , показанных на схеме. В результате получим

Временные характеристики динамического звена

Временной или импульсной характеристикой динамического звена называют реакцию звена на , обозначая ее как . При этом схема эксперимента имеет вид

Выясним, что представляет собой временная характеристика, то есть почему ее называют характеристикой динамического звена?

Для этого рассмотрим динамическое звено с передаточной функцией

В этом случае, в соответствии с (5), имеем

Получаем, что передаточная функция звена это изображение по Лапласу импульсной характеристики динамического звена. В свою очередь, импульсная характеристика может быть определена по передаточной функции

при использовании разложения в форму Хэвисайта и обратное преобразование Лапласа.

Знание импульсной характеристики позволяет определить реакцию динамического звена на сигнал любой формы.

Для динамического звена с передаточной функцией преобразуем (5), используя теорему об умножении изображений преобразования Лапласа,

а если легко получить , тогда

Переходной характеристикой или переходной функцией динамического звена называют реакцию динамического звена на , обозначая ее как . При этом схема эксперимента имеет вид

Для анализа переходной характеристики рассмотрим динамическое звено с передаточной функцией

В этом случае, в соответствии с (5), имеем

По теореме об интегрировании оригинала имеем

Переходная функция является интегралом по времени от импульсной характеристике и наоборот

Переходная характеристика динамического звена может быть определена по передаточной функции

Контрольные вопросы и задачи

Что такое линейное динамическое звено?

Как определить передаточную функцию линейного динамического звена?

Перечислите основные элементы структурных схем систем управления.

Как определить по передаточной функции динамического звена его временные характеристики: импульсную и переходную?

Как по переходной характеристике определить импульсную характеристику динамического звена?

Определите передаточную функцию динамического звена по его принципиальной электрической схеме

Видео:[ТАУ]Записать передаточную функцию устройства [Составить диф. ур-е для условия передачи напряжения]Скачать

Как по дифференциальному уравнению звена найти его передаточную функцию

ИССЛЕДОВАНИЕ ВРЕМЕННЫХ ХАРАКТЕРИСТИК

ДИНАМИЧЕСКИХ ЗВЕНЬЕВ И ИХ СОЕДИНЕНИЙ

Цель работы: для звеньев, заданных передаточными функциями, выбираемыми из табл. 1 прил. 2, и их соединений выполнить следующее:

1) вывести аналитические выражения кривой разгона и импульсной переходной характеристик;

2) построить графические зависимости полученных характеристик при различных значениях постоянных времени и коэффициентов усиления.

Параметры звеньев выбираются из табл. 2 прил. 2 в зависимости от варианта, задаваемого преподавателем.

2.1 Теоретические сведения

Системы автоматического регулирования (САР) принято изображать в виде структурных схем. Структурная схема – это условное изображение, в котором отдельные элементы системы представляются прямоугольниками, а связи между элементами изображаются стрелками, показывающими направление передачи сигнала, н ад которыми ставится условное обозначение сигнала.

Для создания общей методики расчета различных САР было введено понятие динамического звена. Типовым звеном системы автоматического регулирования является составной элемент, имеющий один вход и один выход, и описываемый дифференциальным уравнением не выше второго порядка. На структурной схеме объектов управления звенья изображаются в виде прямоугольников, внутри которых записывается передаточная функция звена (рис. 1).

Рисунок 1. Пример изображения звена на структурных схемах

Как по дифференциальному уравнению звена найти его передаточную функцию

Одной из основных динамических характеристик объекта, широко используемых в теории автоматического регулирования, является передаточная функция.

Передаточной функцией объекта называется отношение преобразованного по Лапласу выхода объекта у ( р ) к преобразованному по Лапласу входу х ( р ) при нулевых начальных условиях. Передаточная функция является функцией комплексного переменного p , обозначается W ( p ): . Передаточная функция характеризует динамику объекта по определенному каналу, связывающему вход объекта с выходом. Если в объекте имеется несколько входов, то каждому каналу связи входа с выходом будет соответствовать своя передаточная функция.

Так же, как и дифференциальное уравнение, передаточная функция полностью характеризует динамику объекта. Если задано дифференциальное уравнение объекта, то для получения передаточной функции необходимо преобразовать дифференциальное уравнение по Лапласу и из полученного алгебраического уравнения найти соотношение .

Если известна передаточная функция объекта, то изображение выхода объекта у ( р ) равно произведению передаточной функции на изображение входа х ( р ): .

Любая самая сложная структурная схема может быть изображена с помощью трех основных типов соединения: — параллельного (рис. 2); — последовательного и соединения с обратной связью.

Рисунок 2. Структурная схема параллельного соединения звеньев

При параллельном соединении входные сигналы всех звеньев одинаковы и равны входу системы х ( р ), а выход системы у( р ) равен сумме выходов звеньев.

Запишем уравнения выходных координат каждого звена:

;

Выход всей системы будет равен

Передаточная функция системы: .

Передаточная функция системы параллельно соединенных звеньев равна сумме передаточных функций отдельных звеньев.

Последовательное соединение звеньев. Особенностью является то, что выход предыдущего звена является входом последующего (рис. 3).

Рисунок 3. Структурная схема последовательного соединения звеньев

Уравнения выходных сигналов каждого звеньев имеют вид:

;

Выходной сигнал последнего звена является выходом всей системы , передаточная функция системы:

Таким образом, передаточная функция системы последовательно соединенных звеньев равна произведению передаточных функций отдельных звеньев. Это соотношение справедливо лишь в том случае, если выход каждого звена зависит только от его входа и не зависит от выходной координаты последующего звена.

Рисунок 4. Структурная схема соединения звеньев с обратной связью

W _n ( p )

W _ос ( p )

Соединение звеньев с обратной связью. Обратной связью называют передачу сигнала с выхода звена на его вход (рис. 4), где сигнал обратной связи х _ос алгебраически суммируется с внешним сигналом х ( p ) . Причем, если суммарный сигнал x ₁ ( p ) определяется соотношением x ₁ ( p ) = x ( p ) + x _oc ( p ), то обратная связь называется положительной, если x ₁ ( p ) = = x ( p ) – x _oc ( p ), т.е. сигнал обратной связи вычитают из внешнего сигнала, то обратная связь называется отрицательной.

В линии обратной связи в общем случае может быть включено звено, в котором выходной сигнал y ( p ) преобразуется в соответствии с передаточной функцией W _oc ( p ) в сигнал x _oc ( p ). Иногда это звено может отсутствовать, т.е. W _oc ( p ) = l и х_ос ( p ) = у ( p ) .

Найдем соотношение между передаточной функцией замкнутой системы W _зс ( p ) и передаточными функциями отдельных звеньев W _n ( p ) и W _oc ( p ). Уравнения выходных сигналов каждого звена

;

Исключив из полученной системы уравнений x ₁ ( p ) и x _ос ( p ), получим , или

откуда передаточная функция замкнутой системы с положительной обратной связью : ,

передаточная функция замкнутой системы с отрицательной обратной связью: .

В реальных условиях на объект управления оказывают влияние внешние воздействия, которые называют возмущающими. Возмущающие воздействия (возмущения) вызывают отклонение регулируемого параметра от заданного значения.

Возмущения, действующие на САР, представляют собой непрерывные функции времени с различными законами изменения. В этом случае возникают трудности принципиального характера, так как заранее неизвестны законы измерения внешних воздействий, что затрудняет анализ динамики и статики САР. Для ликвидации возникших затруднений часто используют так называемые типовые, управляющие и возмущающие воздействия, которые представляют собой либо наиболее вероятные, либо наиболее неблагоприятные законы изменения управляющих и возмущающих воздействий. Например, довольно широко в качестве типовых используют воздействия полиномиального вида:

где n = 0, 1, 2, … – натуральные числа; – постоянные величины; 1 ( t ) – единичная ступенчатая функция,

При n = 0 имеем единичное ступенчатое воздействие: .

При n = 1 получим линейное воздействие: .

На рис. 5 представлены графики единичного ступенчатого и линейного входных воздействий.

Рисунок 5. Типовые полиномиальные воздействия

В некоторых случаях в качестве типового используется единичное импульсное воздействие следующего вида: , где d ( t ) – единичная дельта-функция

Единичная дельта-функция (единичный импульс) представляет собой математическую идеализацию импульса бесконечно малой длительности, бесконечно большой амплитуды, имеющего конечную площадь, равную единицы, т.е. .

Момент приложения внешних воздействий к САР обычно принимается за ноль отсчёта времени. При таком подходе внешние воздействия для отрицательного момента времени равны нулю. В аналитические выражения для внешних воздействий в качестве множителя вводят единичную ступенчатую функцию.

Важнейшей характеристикой САР и её составных элементов являются переходные и импульсные переходные (импульсные) функции. Графическое представление переходных и импульсных функций называют временными характеристиками. Переходной функцией h ( t ) называют функцию, описывающую сигнал на выходе при условии, что на вход подано единичное ступенчатое воздействие, при нулевых начальных условиях. График переходной функции, представляющий собой зависимость функции h ( t ) от времени t , называют переходной характеристикой. В том случае, если амплитуда единичного ступенчатого воздействия отлична от единицы получают разновидность переходной характеристики, которая называется кривой разгона.

Импульсной или весовой функцией w ( t ) называют функцию, описывающую реакцию на единичное импульсное воздействие при нулевых начальных условиях. График зависимости функции w ( t ) от времени называют импульсной переходной (импульсной) характеристикой.

Любое внешнее воздействие сложной формы может быть приближенно представлено в виде совокупности типовых воздействий, связанных между собой определенными математическими операциями.

Аналитическое определение переходных функций и характеристик основано на следующих положениях. Если задана передаточная функция системы или составной части W ( p ) и известен входной сигнал x ( t ), то выходной сигнал y ( t ) определяется следующим соотношением: .

Таким образом, изображение выходного сигнала представляет собой произведение передаточной функции на изображение входного сигнала . Сигнал y ( t ) в явном виде получим после перехода от изображения к оригиналу y ( t ).

Так как изображение единичного ступенчатого воздействия равно , то изображение переходной функции определяется соотношением: . Следовательно, для нахождения переходной функции необходимо передаточную функцию разделить на p и выполнить переход от изображения к оригиналу.

Изображение единичного импульса равно 1. Тогда изображение импульсной функции — . Таким образом, передаточная функция является изображением импульсной функции.

Так как , то между импульсной и переходной функциями существует следующая зависимость: .

Импульсная и переходная функции, как и передаточная функция, являются исчерпывающими характеристиками системы при нулевых начальных условиях. По ним можно определить выходной сигнал при произвольных входных воздействиях.

В работе рассматриваются следующие звенья:

1) идеальное интегрирующее : ;

2) реальное интегрирующее : ;

3) апериодическое 1-го порядка: ;

4) апериодическое 2-го порядка: ;

5) реальное дифференцирующее : ;

6) колебательное ( 0 x ): ;

7) консервативное : ;

8) звено запаздывания: ,

где k – коэффициент пропорциональности (коэффициент усиления); T – постоянная времени интегрирования, с; t – время запаздывания, с; 0 x – коэффициент затухания колебаний (коэффициент демпфирования).

2.2 Алгоритм выполнения работы

1. Записать передаточную функцию звена с нулевыми начальными условиями.

2. Определить вид переходных процессов с учетом единичного ступенчатого и импульсного воздействий.

3. Построить графики переходных процессов при различных значениях постоянных времени и коэффициента усиления. Рассмотреть следующие случаи: — при табличных значениях параметров ( k и T ); — изменив значения коэффициентов усиления с исходными значениями постоянных времени; — изменив значения постоянных времени и исходных значениях коэффициентов усиления.

2.3 Примеры расчета

Для звеньев и соединения звеньев, заданных передаточными функциями: , ,

построить переходные процессы при различных значениях постоянных времени и коэффициента усиления.

1. Передаточная функция реального дифференцирующего звена: , откуда , где – единичное ступенчатое воздействие, или – единичная импульсная функция, следовательно: , .

2. Выполним обратное преобразование Лапласа (табл. 3 прил. 1) и получим переходной процесс для единичного ступенчатого воздействия: . Между импульсной и переходной функциями существует следующая зависимость , то .

3. Строим временные характеристики звена, рис. 6.

Рисунок 6. Временные характеристики реального дифференцирующего звена

4. Передаточная функция апериодического звена второго порядка: , откуда .

Учитывая единичное ступенчатое воздействие или единичную импульсную функцию, получим соответственно:

5. Выполним обратное преобразование Лапласа (см. табл. 3 прил. 1) и получим переходной процесс для единичного ступенчатого воздействия .

Импульсная функция .

6. Строим временные характеристики звена (рис. 7).

Рисунок 7. Временные характеристики апериодического звена II -го порядка

7. Передаточная функция для последовательного соединения звеньев . Для последовательно соединенных реального дифференцирующего звена и апериодического звена второго порядка передаточная функция запишется следующим образом:

где k ₁ – коэффициент усиления; k ₂ – коэффициент усиления апериодического звена второго порядка; T ₁ – постоянная времени реального дифференцирующего звена; T ₂ , T ₃ – постоянные времени апериодического звена второго порядка.

Учитывая единичное ступенчатое воздействие или единичную импульсную функцию, получим соответственно: