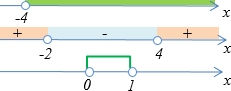
Как перейти от неравенств к уравнениям (4 видео)

Как перейти от неравенства к уравнению

Переход от неравенств к уравнениям в задачах математического программирования

Все неравенства, описанные выше определяют некоторое множество значений величин х₁, х₂, х_n, которые удовлетворяют этим неравенствам. Покажем как от системы неравенств перейти к равенстам вводя дополнительные переменные.

Рассмотрим линейное неравенство:

a₁х₁+а₂х₂+…+x_nx_n b, (7)

добавим к левой части некоторую неотрицательную величину х_n+1 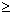0 (8) Интегрирование выражений, содержащих квадратный трехчлен Математика вычисление интеграла [an error occurred while processing this directive]

Неотрицательное значение переменной х_nн 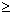0 называется дополнительной переменной.

Перепишем сформулированные выше задачи в виде условий типа равенств с введением дополнительных переменных.

Задача использования сырья

(10)

где х_n+1,… х_n+m — дополнительные положительные переменные, соответствующие им коэффициенты в целевой функции с_n+1=…c_n+m=0

53-54. Общая задача оптимизации. Постановка и различные формы записи задач линейного программирования (ЗЛП).

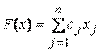
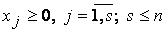
Опр.1Стандартной (или симметричной) задачей линейного программирования называется задача, которая состоит в определении максимального для «≤» (минимального для «≥») значения функции при выполнении условий и , где k = m, s = n.

Канонической формой ЗЛП называется такая, в которой все ограничения представляют уравнение с неотрицательными свободными членами.

55. Определение плана, невырожденного и вырожденного опорного плана (ОП), оптимального плана.

План, соответствующий вершине допустимой области, называется опорным планом.

Заметим, что для всех полученных решений число заполненных
(отличных от нуля) клеток транспортной таблицы в точности равно числу базисных переменных задачи, т. е. 6.

Определение 4.3.Если при решении транспортной задачи число заполненных клеток транспортной таблицы равно т+п-1, где т – число производителей, п – число потребителей, то план перевозок невырожденный.

Определение 4.4. Если число заполненных клеток транспортной таблицы меньше т+п-1, то план перевозок вырожденный.

Вырожденный план перевозок получится, если на каком-то шаге одновременно удовлетворяется спрос потребителя и исчерпывается предложение соответствующего поставщика, т. е. одновременно вычеркивается строка и столбец.

Для нахождения оптимального плана перевозок необходимо уметь расценивать полученный план наоптимальность. Как это сделать, не имея в распоряжении всех возможных планов перевозок, которые можно было бы сравнить между собой? Для оценки плана на оптимальность вводится понятие косвенных затрат. Косвенные затраты — это затраты, получаемые для маршрутов, по которым не осуществляются перевозки при данном плане. Рассчитанные косвенные затраты сравниваются с реальными затратами, которые имели бы место, если бы перевозки по данным маршрутам осуществлялись. Если для всех невыбранных маршрутов косвенные затраты не больше реальных, то данный план перевозок является оптимальным. Если хотя бы для одного маршрута косвенные затраты больше реальных, то план перевозок может быть улучшен путем введения в него данного маршрута. Ввод нового маршрута в план перевозок соответствует вводу в список базисных переменных переменной транспортной задачи, соответствующей этому маршруту. Эти рассуждения лежат в основе ряда методов, применяемых для нахождения оптимального плана перевозок. Рассмотрим один из них — метод потенциалов.

Получение оптимального плана транспортной задачис использованием метода потенциалов

Шаг 1.Получение начального плана перевозок по методу «северо-западного» угла, минимального элемента, Фогеля или любым другим методом.

Шаг 3.Проверка плана на невырожденность. Если полученный план вырожденный, формально заполняют нулями некоторые из свободных клеток так, чтобы общее число занятых клеток было равно т+п-1. Нули надо расставлять так, чтобы не образовался замкнутый цикл из занятых клеток. (Определение цикла будет дано чуть ниже)

Шаг 3.Проверка плана на оптимальность.

Шаг 3.1.Определение потенциалов производителей и потребителей. Составляют систему уравнений для заполненных клеток транспортной таблицы: U_i + V_j = С_ij , где i,j – номера строк и столбцов на пересечении которых стоят заполненные клетки, U_i – потенциал i-го поставщика,
V_j – потенциал j-го потребителя, С_ij – тариф на перевозку из пункта i
в пункт j. Число уравнений в системе равно т+п-1, а число неизвестных U_i – и V_j равно т+п. Для решения данной системы одно из неизвестных выбирают произвольно. Обычно полагают U_i = 0. Решая систему уравнений, находят значения потенциалов U_i и V_j, ; .

Шаг 3.2.Определение суммы потенциалов (косвенных тарифов) для свободных клеток: C1_qp = U_q + V_p , где q и р – номера строк U столбцов, на пересечении которых стоит свободная клетка, U_q – потенциал q-гo поставщика, V_p – потенциал р-го потребителя, C1_qp – косвенные тарифы.

Шаг 3.3.Проверка на оптимальность.

Для каждой свободной клетки транспортной таблицы составляется разность между C1_qp и C_qp (косвенным и реальным тарифами) ∆ _qp =
= C1_qp – C_qp. Если все ∆ _qp ≤ 0, то полученный план оптимален. Если хотя бы для одной свободной клетки ∆ _qp > 0, то план может быть улучшен. Переход к шагу 4.

Шаг 4.Улучшение плана.

Шаг 4.1.Выбор переменной, вводимой в список базисных переменных.

Выбирают клетку, которой соответствует максимальное положительное значение разности, полученной на шаге 3.3. Если имеется несколько одинаковых значений, то из них выбирают любое.

Переменная транспортной задачи, соответствующая этой клетке, вводится в список базисных переменных, т. е. данная клетка транспортной таблицы заполняется.

Шаг 4.2.Выбор переменной, выводимой из списка базисных переменных.

Заполнение клетки, выбранной на шаге 4.1, происходит следующим образом. Строят цикл, начинающийся и заканчивающийся в выбранной свободной клетке, содержащий в качестве вершин заполненные клетки таблицы и состоящий из горизонтальных и вертикальных отрезков. При этом в каждой клетке таблицы, являющейся вершиной цикла, соединяют обязательно горизонтальный и вертикальный отрезки. В свободной клетке условно ставят знак «+», а в остальных вершинах цикла, чередуясь, ставят «-» и «+». Затем происходит перераспределение продукции по циклу. Для этого выбирают клетку со знаком «-» , которой соответствует наименьшее число единиц продукции. Это значение прибавляют к значениям, стоящим в клетках со знаком «+» , и отнимают от значений, стоящих в клетках со знаком «-» . При таком перераспределении общий баланс не изменяется. Свободная клетка заполняется. А клетка со знаком «-» , которой соответствует наименьшее количество продукции, становится свободной; соответствующую ей переменную исключают из списка базисных.

Для нового плана повторяют все действия, т. е.. переходят к шагу 3.

Содержание

Равносильные неравенства, преобразование неравенств
Равносильные неравенства: определение, примеры
Равносильные преобразования неравенств
Результат неравносильных преобразований неравенств
40. Алгебра Читать 0 мин.
40.710. Равносильные системы
🔍 Видео

Видео:✓ Как решать логарифмические уравнения и неравенства, не помня свойства логарифмов | Борис ТрушинСкачать

Равносильные неравенства, преобразование неравенств

В процессе решения неравенств зачастую происходит переход от заданного неравенства к неравенствам иного вида, имеющим то же решение, но определяемое проще. Иными словами, в результате преобразований заданное неравенство возможно заменить равносильным ему, облегчающим поиск решения. Данная статья посвящена способам равносильных преобразований. Сформулируем определение, рассмотрим основные виды преобразований.

Видео:Подготовка к ОГЭ . Рациональные неравенства | Математика | TutorOnlineСкачать

Равносильные неравенства: определение, примеры

Равносильные неравенства – неравенства, имеющие одни и те же решения. В частном случае, неравенства, не имеющие решений, тоже называются равносильными.

Иными словами, если неравенства равносильны и имеют решения, то любое решение первого будет являться и решением второго. Ни одно из равносильных неравенств не имеет решений, не являющихся решениями других, равносильных ему неравенств.

Даны три равносильных неравенства: x > 2 , 2 · x : 2 > 2 и x > 3 — 1 . В самом деле, множества решений этих неравенств одинаковые, решение каждого их них – числовой промежуток ( 2 , + ∞ ) .

Неравенства х 6 ≥ — 2 и | х + 7 | 0 являются равносильными, поскольку оба не имеют решений.

Неравенства х > 3 и х ≥ 3 – не равносильные: х = 3 служит решением второго из этих равенств, но не служит решением первого.

Отметим, что указанное определение относится к неравенствам как с одной переменной, так и с двумя, тремя и более.

Видео:Как решать уравнения и неравенства? | Ботай со мной #072 | Борис Трушин |Скачать

Равносильные преобразования неравенств

Возможно совершить некоторые действия с правой и левой частью неравенств, что даст возможность получать новые неравенства, имеющие решения, как и у исходного.

Равносильное преобразование неравенства – это замена исходного неравенства равносильным ему, т.е. таким, которое имеет то же множество решений. Сами действия-преобразования, приводящие к равносильному неравенству, тоже называют равносильными преобразованиями.

Равносильные преобразования дают возможность находить решения неравенств, преобразуя заданное неравенство в равносильное ему, но более простое и удобное для решения.

Рассмотрим основные виды равносильных преобразований: по сути без них не обходится решение ни одного неравенства. Отметим также, что равносильные преобразования неравенств очень похожи на равносильные преобразования уравнений. Схожи и принципы доказательства, только, конечно, в данном случае доказательства будут строиться на основе свойств числовых неравенств.

Итак, перечислим основные виды равносильных преобразований неравенств:

Замена выражений в обоих частях неравенства тождественно равными выражениями на области допустимых значений (ОДЗ) переменных заданного неравенства есть равносильное преобразование неравенства.

Доказательство 1

Докажем утверждение. Пусть дано неравенство с одной переменной A ( x ) B ( x ) , где A ( x ) и B ( x ) — некие выражения с переменной x . Допустим, выражение C ( x ) является тождественно равным выражению A ( x ) , а выражение D ( x ) является тождественно равным B ( x ) на ОДЗ заданного неравенства. Найдем доказательство, что неравенство C ( x ) D ( x ) служит равносильным неравенству A ( x ) B ( x ) . С этой целью нам нужно продемонстрировать тот факт, что любое решение q заданного неравенства будет также решением неравенства C ( x ) D ( x ) , и наоборот: любое решение неравенства C ( x ) D ( x ) будет решением заданного неравенства A ( x ) B ( x ) .

Мы приняли, что q – решение неравенства A ( x ) B ( x ) , тогда верным будет числовое неравенство A ( q ) B ( q ) . Отсюда по разностному определению неравенства выводим, что A ( q ) − B ( q ) 0 .

Выражение A ( q ) − B ( q ) можно записать в виде A ( q ) + ( C ( q ) − C ( q ) ) − B ( q ) + ( D ( q ) − D ( q ) ) , что является тем же самым, ( A ( q ) − C ( q ) ) + C ( q ) − ( B ( q ) − D ( q ) ) − D ( q ) . Выражения A ( x ) и C ( x ) , B ( x ) и D ( x ) по условию тождественно равны, тогда: A ( q ) = C ( q ) и B ( q ) = D ( q ) , откуда A ( q ) − C ( q ) = 0 и B ( q ) − D ( q ) = 0 . Таким образом, ( A ( q ) − C ( q ) ) + C ( q ) − ( B ( q ) − D ( q ) ) − D ( q ) = 0 + C ( q ) − 0 − D ( q ) = C ( q ) − D ( q ) . Мы продемонстрировали, что значение выражения A ( q ) − B ( q ) равно значению выражения C ( q ) − D ( q ) , а поскольку A ( q ) − B ( q ) 0 , то и C ( q ) − D ( q ) 0 . Отсюда делаем вывод, что C ( q ) D ( q ) . И крайнее неравенство означает, что q – решение неравенства C ( x ) D ( x ) .

Таким же образом доказывается, что любое решение неравенства C ( x ) D ( x ) будет решением и неравенства A ( x ) B ( x ) , тем самым будет доказано и исходное утверждение.

Подобные преобразования не должны сужать ОДЗ заданного неравенства, тогда возможно совершать тождественные преобразования обеих сторон неравенства.

Покажем пример использования.

Рассмотрим неравенство x > 2 + 6 . В правой части возможно заменить сумму значением так, чтобы получилось равносильное неравенство x > 8 .

В неравенстве 3 · ( x + 1 ) − 2 · x + 11 ≤ 2 · y + 3 · ( y + 1 ) + x , в обоих его частях мы раскроем скобки и приведем подобные слагаемые, получив в итоге равносильное неравенство x + 14 ≤ 5 · y + 3 + x . Если детально разобрать наши действия, то мы заменили левую часть данного неравенства тождественно равным ей выражением x + 14 , а правую часть – тождественно равным ей выражением 5 · y + 3 + x на области допустимых значений переменных x и y заданного неравенства.

Еще раз особенно укажем, как важен учет ОДЗ (область допустимых значений) при совершении замены частей неравенства тождественными выражениями. В случае, когда ОДЗ нового неравенства будет отлична от ОДЗ исходного, неравенство не может считаться равносильным. Это крайне важный аспект, пренебрежение им приводит к неверным ответам при решении неравенств.

Прибавление или вычитание из обеих частей неравенства одного и того же числа является равносильным преобразованием.

Доказательство 2

Приведем обоснование указанного утверждения. Допустим, задано неравенство A ( x ) B ( x ) и некое число c . Необходимо доказать, что заданному равносильно неравенство A ( x ) + c B ( x ) + c , которое мы получим, прибавив к обеим частям исходного неравенства число c . Продемонстрируем, что любое решение q заданного неравенства будет также и решением неравенства A ( x ) + c B ( x ) + c , и наоборот.

Мы приняли, что q – решение неравенства A ( x ) B ( x ) , тогда верно следующее: A ( q ) B ( q ) . Из свойств числовых неравенств следует, что к обеим частям верного числового неравенства можно прибавить любое число. Мы прибавим число c к обеим частям крайнего неравенства, получим A ( q ) + c B ( q ) + c , и это означает, что q служит решением неравенства A ( x ) + c B ( x ) + c .

Подобным же образом можно доказать, что любое решение неравенства A ( x ) + c B ( x ) + c будет являться и решением неравенства A ( x ) B ( x ) . Мы приняли, что q — решение неравенства A ( x ) + c B ( x ) + c , тогда A ( q ) + c B ( q ) + c , из обеих частей вычтем число c , получим A ( q ) B ( q ) , где q – решение неравенства A ( x ) B ( x ) .

Таким образом, неравенства A ( x ) B ( x ) и A ( x ) + c B ( x ) + c являются равносильными. Для наглядности укажем пример: x > 2 и x − 5 > 2 − 5 – равносильные неравенства, а, учитывая рассматриваемое выше утверждение, равносильным им является и неравенство x − 5 > − 3 .

Свойство, которое мы доказали выше, возможно расширить: прибавив к левой и правой частям неравенства одно и то же выражение с учетом соблюдения ОДЗ данного неравенства, получим равносильное неравенство.

Пример 3

Исходному неравенству x 7 будет равносильно неравенство x + ( 12 · x − 1 ) 7 + ( 12 · x − 1 ) .

Указанные выше равносильные преобразования дают как следствие еще одно действие, пожалуй, основное в процессе преобразования неравенств: перенос любого слагаемого из одной части неравенства в другую с противоположным знаком служит равносильным преобразованием.

Пример 4

Исходному неравенству 3 · x − 5 · y > 12 равносильно неравенство 3 · x > 12 + 5 · y .

Равносильным преобразованием также является умножение или деление обеих частей неравенства на одно и то же положительное число. И, умножив (или разделив) обе части неравенства на одно и то же отрицательное число, поменяв при этом знак неравенства на противоположный ( на > , > на , ≤ на ≥ , а ≥ на ≤ ), получим равносильное неравенство.

Доказательство 3

Докажем сначала первую часть утверждения. Допустим, задано неравенство A ( x ) B ( x ) и c – некое положительное число. Приведем доказательство, что A ( x ) B ( x ) и A ( x ) · c B ( x ) · c — равносильные неравенства. Примем q как решение заданного неравенства, в таком случае верным будет числовое неравенство A ( q ) B ( q ) . Опираясь на свойства числовых неравенств, можем утверждать, что, умножив обе части верного числового неравенства на положительное число, получим верное числовое неравенство. Производим умножение на заданное число c , что дает нам A ( q ) · c B ( q ) · c . Это значит, что q — решение неравенства A ( x ) · c B ( x ) · c .

Теперь в обратную сторону: примем q как решение неравенства A ( x ) · c B ( x ) · c , в таком случае: A ( q ) · c B ( q ) · c . Разделим обе части этого числового неравенства на положительное число c (опираясь на свойства числовых неравенств), что даст нам верное числовое неравенство A ( q ) B ( q ) . Отсюда можно сделать вывод, что q — решение неравенства A ( x ) B ( x ) . Так, мы доказали, что при положительном числе c неравенства A ( x ) B ( x ) и A ( x ) · c B ( x ) · c являются равносильными.

Таким же образом приводится доказательство второй части утверждения. Здесь можно опереться на свойство умножения и деления числовых неравенств на отрицательное число при смене знака неравенства на противоположный.

Задано неравенство 2 · x ≤ 5 . Умножим его левую и правую части на положительное число 3 , что даст нам равносильное неравенство 6 · x ≤ 15 .

Задано неравенство — 2 3 · z 1 . Разделим левую и правую его части на отрицательное число — 2 3 , сменив знак неравенства. Получим z > — 1 1 2 — неравенство, равносильное заданному.

Расширим и это свойство неравенств:

умножив обе части заданного неравенства на одно и то же выражение, положительное при любых значениях переменных из ОДЗ заданного неравенства, не изменяющее ОДЗ, получим равносильное неравенство;
умножив обе части неравенства на одно и то же выражение, отрицательное при любых значениях переменных из ОДЗ заданного неравенства и не изменяющее ОДЗ, а также изменив знак равенства на противоположный, получим равносильное неравенство.

Пример 7

Задано неравенство x > 1 . Умножим его правую и левую части на выражение x 2 + 1 , положительное на всей ОДЗ, и получим равносильное неравенство x · ( x 2 + 1 ) > 1 · ( x 2 + 1 ) .

В целом, есть и другие равносильные преобразования, однако, они не так распространены и скорее имеют отношение к конкретному виду неравенств, например, к логарифмическим неравенствам. Познакомиться с ними можно подробнее в соответствующей теме.

Видео:Система уравнений VS Система неравенств. ОГЭ по математике №9, 13| Математика TutorOnlineСкачать

Результат неравносильных преобразований неравенств

Сколь уж существуют равносильные преобразования, имеют место и неравносильные. Такие действия приводят к искажению заданного неравенства и дают в итоге решение, не являющееся истинным для исходного неравенства. Случается, что и при неравносильных преобразованиях получается верный ответ, но это не более чем случайность.

Собственно, вывод очевиден: решая неравенства, производить только равносильные преобразования.

Разберем примеры для лучшего понимания теории.

Пусть заданы неравенства x > − 2 и 1 x — 1 x + x > — 2 . Решением первого будет числовой промежуток ( − 2 , + ∞ ) , а второго – множество — 2 , 0 ∪ 0 , + ∞ .

Пусть необходимо решить второе неравенство.

Конечно, сазу приходит мысль об упрощении левой части приведением слагаемых, произведя замену просто на х, что даст переход к простому неравенству x > − 2 . Однако мы намеренно не учтем, что переход надо осуществить на ОДЗ переменной х ( х ≠ 0 ) , тогда предложенное выше преобразование даст нам неравносильное неравенство x > − 2 , а следовательно – неверный ответ ( − 2 , + ∞ ) взамен нужного — 2 , 0 ∪ 0 , + ∞ .

Посмотрим с другой стороны:

Мы решим неравенство x > − 2 . При этом нам захотелось заменить его якобы равносильным неравенством 1 x — 1 x + x > — 2 . Однако оно не является таковым: нуль не служит его решением, однако служит решением исходного неравенства. Суть в том, что выражение в его левой части тождественно равно не на всей области допустимых значений исходного неравенства: когда х = 0 , неравенство не равно x (при х = 0 оно не определено). Совершенные действия приведут нас к неверному ответу — 2 , 0 ∪ 0 , + ∞ взамен правильного ( − 2 , + ∞ ) .

Признак вероятного неравносильного преобразования – сужение области допустимых значений. Вновь обратимся к примеру выше: когда мы производили переход от неравенства x > − 2 к неравенству 1 x — 1 x + x > — 2 , произошло сужение ОДЗ со всего множества действительных чисел до множества без нуля. Такое положение вещей точно указывает на то, что полученное в итоге неравенство никак не будет равносильным исходному, т.е. такой переход не приведет к необходимому верному результату.

Неравносильные преобразования чаще всего происходят при невнимательном использовании свойств корней, логарифмов и модуля. Эти моменты будут детально рассмотрены в темах о решении неравенств соответствующих видов.

Видео:Как понять неравенства? Квадратные неравенства. Линейные и сложные неравенства | TutorOnlineСкачать

40. Алгебра Читать 0 мин.

Видео:Равносильность уравнений и неравенств. Видеоурок 7. Алгебра 10 классСкачать

40.710. Равносильные системы

Два неравенства являются равносильными, если множества их решений совпадают. При решении неравенств иногда приходится переходить от одного неравенства к другому, более простому. Рассмотрим несколько равносильных переходов: для решения иррациональных, показательных, логарифмических неравенств, неравенств с модулем, дробно-рациональных неравенств.

1. Равносильные переходы для решения иррациональных неравенств

Для избавления от радикалов в иррациональных неравенствах требуется умение возводить обе части неравенства в соответствующую степень. Однако нужно быть осторожными при возведении в четную степень, если хотя бы одна из частей неравенства отрицательная. Неосторожное возведение в квадрат неравенства может повлечь за собой приобретение или потерю решений.

Корни четной степени извлекаются только из неотрицательных чисел, это непосредственно относится к возведению корня четной степени $ sqrt[2n] $ в соответствующую четную степень, после чего $f(x)$ стоит уже не под корнем, а значит, лишено неявного ограничения $f(x)geq 0$. Следовательно, это неявное ограничение мы должны учесть, однако, учитываем мы его для меньшего подкоренного выражения (т.к. для большего это ограничение выполнится автоматически).

$sqrt[2n]geq sqrt[2n]leftrightarrow left< begin f(x)geq g(x) \ g(x)geq 0. end right. $

Пример. Решите неравенство

Решение. Применим равносильный переход:

$left< begin x^-5x+6geq 0 \ (x-3)(x-1)geq 0 end right. leftrightarrow left< begin (x-2)(x-3)geq 0 \ (x-3)(x-1)geq 0 end right. $

Видим, что решением системы является промежуток $xin (-infty ;1]cup lbrack 3;infty )$

Ответ: $xin (-infty ;1]cup lbrack 3;infty )$

Встречаются такие неравенства, в которых корень сравнивают с выражением. Тогда тоже пользуемся возведением в квадрат для избавления от иррациональности, однако, накладываем дополнительное ограничение – неотрицательность выражения, поскольку значение корня четной степени – число неотрицательное.

$sqrt[2n] &lt g(x) leftrightarrow left < begin f(x)&lt g^(x), \ f(x)geq 0, \ g(x)>0. end right. $

$sqrt[2n]leq g(x)leftrightarrow left< begin f(x)leq g^(x), \ f(x)geq 0, \ g(x)geq 0. end right. $

Пример. Решите неравенство

$sqrt 0 end right. leftrightarrow left< begin x+5 -7 end right. leftrightarrow left< begin x^-15x+44>0 \ xgeq -5 \ x 0 \ xgeq -5 \ x g(x)leftrightarrow left[ begin left< begin f(x)>g^(x) \ g(x)geq 0, end right. \ left< begin f(x)geq 0, \ g(x) 7-x$

Воспользуемся равносильным переходом.

Пример. Решите неравенство $sqrt[3]>sqrt[3]$

Решение. Воспользуемся равносильным переходом:

$x 1$, тогда неравенство $a^vee a^$ равносильно неравенству $fvee g$.

В этом правиле последнее неравенство имеет тот же знак, что и первое, т.к. показательная функция с основанием $a>1$ возрастает.

Пример. Решите неравенство: $0,1^<x^+4x> 0;$

Ответ $xin (-infty ;-2)cup (-2;+infty )$.

Ответ: $xin (-infty ;-2)cup (-2;+infty )$

Если неизвестная входит как в основание, так и в показатель степени, то заранее неизвестно, будет ли основание степени больше или меньше единицы, поэтому при решении неравенства нужно учитывать оба этих случая. Если неравенство строгое, то получаем следующий равносильный переход:

$(phi (x))^ &gt (phi (x))^Leftrightarrow left[ begin left< begin f(x)>g(x) \ phi (x) &gt 1 end right. \ left< begin f(x) &lt g(x) \ 0 &lt phi (x) (x+5)^$

Используем следующий равносильный переход:

Если неравенство нестрогое, то нужно дополнительно рассмотреть случай – основание равно единице, т.к. тогда получается, что единица в любой степени равна единице, неравенство выполнится. Т.е. получаем следующий равносильный переход:

$(phi (x))^geq (phi (x))^Leftrightarrow left[ begin left< begin f(x)>g(x) \ phi (x)>1 endright. \ left< begin f(x) &lt g(x) \ 0 0 end right. leftrightarrow left< begin xneq 0 \ x>0 end right. $

Используем следующий равносильный переход:

$left[ begin left< begin x^geq -(x^-4) \ fracx>1 end right. \ left< begin x^leq -(x^-4) \ 0 &lt fracx &lt 1 end right. \ fracx=1 end right. leftrightarrow left[ begin left< begin x^+x^-4geq 0 \ x>frac end right. \ left< begin x^+x^-4leq 0 \ 0 &lt frac<>x &lt frac end right. \ x=frac end right. leftrightarrow left[ begin left< begin 2x^+4geq 0 \ x>frac end right. \ left< begin 2x^+4leq 0 \ 0 &lt x &lt frac end right. \ x=frac end right. leftrightarrow left[ begin left< begin 2(x^+2)geq 0 \ x>frac end right. \ left< begin 2(x^+2)leq 0 \ 0 &lt x &lt frac end right. \ x=frac end right. leftrightarrow $

Таким образом, решение неравенства: $xin lbrack frac;infty )$

Ответ $xin lbrack 2,25;infty )$

3. Равносильные переходы для решения логарифмических неравенств

Метод решений простейших логарифмических неравенств опирается на монотонность логарифмической функции, т.е. на правило отбрасывания логарифмов. Однако есть отличие от аналогичного правила отбрасывания оснований, которое объясняется тем, что при отбрасывании логарифмов расширяется ОДЗ неравенства. Значит, выражения, стоящие под логарифмами после отбрасывания последних могут стать отрицательными или равными нулю, следовательно, мы должны дополнительно учесть, что подлогарифмическое выражение положительно.

Если неизвестная входит как в основание, так и под знак логарифма, то заранее неизвестно, будет ли основание больше или меньше единицы, поэтому при решении неравенства нужно учитывать оба этих случая.

Воспользуемся равносильным переходом:

$left[ begin left< begin 2-x>1+x \ 2-x>0 \ 1+x>0 \ 1+x>1 end right. \ left< begin 2-x &lt 1+x \ 2-x>0 \ 1+x>0 \ 0 &lt 1+x &lt 1 end right. end right. leftrightarrow left[ begin left< begin -x-x>1-2 \ -x>-2 \ x>-1 \ x>0 end right. \ left< begin -x-x &lt 1-2 \ -2> \ -1> \ -1 &lt x &lt 0 end right. end right. leftrightarrow left[ begin left< begin -2x>-1 \ x &lt 2 \ x>-1 \ x>0 end right. \ left< begin -2x &lt -1 \ x &lt 2 \ x>-1 \ end right. end right. leftrightarrow left[ begin left< begin x &lt 0,5 \ x &lt 2 \ x>-1 \ x>0 end right. \ left< begin x>0,5 \ x &lt 2 \ x>-1 \ end right. end right. $

Решением первой системы является интервал (0;0,5)

При решении неравенств второй системы видим, что пересечений решений нет.

Таким образом, решением совокупности является интервал (0;0,5)

Пример. Решите неравенство

Воспользуемся равносильным переходом:

$left[ begin left< begin x^-2x-8geq x^ \ x^-2x-8>0 \ x^>0 \ x>1 end right. \ left< begin x^-2x-8leq x^ \ x^-2x-8>0 \ x^>0 \ 0 &lt x &lt 1 end right. end right. leftrightarrow left[ begin left< begin x^-2x-8-x^geq 0 \ (x-4)(x+2)>0 \ xneq 0 \ x>1 endright. \ left< begin x^-2x-8-x^leq 0 \ (x-4)(x+2)>0 \ xneq 0 \ 0 &lt x &lt 1 end right. end right. leftrightarrow left[ begin left< begin -2x-8geq 0 \ (x-4)(x+2)>0 \ xneq 0 \ x>1 end right. \ left< begin -2x-8leq 0 \ (x-4)(x+2)>0 \ xneq 0 \ 0 &lt x &lt 1 end right. end right. $

$left[ begin left< begin -2(x+4)geq 0 \ (x-4)(x+2)>0 \ xneq 0 \ x>1 end right. \ left< begin -2(x+4)leq 0 \ (x-4)(x+2)>0 \ xneq 0 \ 0 &lt x &lt 1 end right. end right. leftrightarrow left[ begin left< begin x+4leq 0 \ (x-4)(x+2)>0 \ xneq 0 \ x>1 end right. \ left< begin x+4geq 0 \ (x-4)(x+2)>0 \ xneq 0 \ 0 &lt x &lt 1 end right. end right. $

$left< begin x+4leq 0 \ (x-4)(x+2)>0 \ xneq 0 \ x>1 end right. leftrightarrow left< begin xleq -4 \ (x-4)(x+2)>0 \ xneq 0 \ x>1 end right. $

видим, что для указанной системы нет решений, т.к. и $x>1$

$left< begin x+4geq 0 \ (x-4)(x+2)>0 \ xneq 0 \ 0 &lt x &lt 1 end right. leftrightarrow left< begin xgeq -4 \ (x-4)(x+2)>0 \ xneq 0 \ 0 &lt x &lt 1 end right. $

$left< begin xgeq -4 \ (x-4)(x+2)>0 \ xneq 0 \ 0 &lt x &lt 1 endright. $

При нанесении решений каждого неравенства системы на числовую прямую видим, что пересечений решений нет. Значит, неравенство не имеет решений.

Ответ: решений нет.

4. Равносильные переходы для решения неравенств, содержащих знак модуля

Если модуль меньше функции, то избавляемся от модуля, но взамен получаем систему из двух неравенств. Учитываем случаи: если число под модулем положительно и если число под модулем отрицательно:

$leftvert f(x)rightvert &ltg(x) leftrightarrow left< begin f(x) &lt g(x) \ f(x)>-g(x), end right. $

$leftvert f(x)rightvert leq g(x)leftrightarrow left< begin f(x)leq g(x) \ f(x)geq -g(x), end right. $

Этот метод работает всегда, даже если выражение $g(x)$ отрицательно. Убедимся в этом на примерах.

Пример. Решите неравенство: -5, end right. leftrightarrow left< begin x &lt 8 \ x>-2 end right. $

Пример. Решите неравенство: $leftvert x-3rightvert &lt -5$

Решение. Воспользуемся равносильным переходом:

$left< begin x-3 &lt -5 \ x-3>-5 end right. leftrightarrow left< begin x &lt -2 \ x>8 endright. $

Ответ: решений нет

Рассмотренный пример наглядно демонстрирует, что метод работает всегда. Мы помним, что модуль числа по определению является величиной неотрицательной. В примере модуль меньше отрицательного числа, очевидно, что такое неравенство не имеет решений.

Пример. Решите неравенство

$leftvert x+4rightvert &lt 2x$

Воспользуемся равносильным переходом.

$left< begin x+4 &lt 2x \ x+4>-2x end right. leftrightarrow left< begin x+4-2x &lt 0 \ x+4+2x>0 end right. leftrightarrow left< begin -x+4 &lt 0 \ 3x+4>0 end right. leftrightarrow left< begin x>4 \ x>-frac end right. $

Решением системы является луч (4;∞).

Ответ: $xin (4;infty )$

Пример. Решите неравенство

$leftvert x+2rightvert leq 5x$

Воспользуемся равносильным переходом.

$left< begin x+2leq 5x \ x+2geq -5x end right. leftrightarrow left< begin x+2-5xleq 0 \ x+2+5xgeq 0 end right. leftrightarrow left< begin -4xleq -2 \ 6xgeq -2 end right. leftrightarrow left< begin xgeq 0,5 \ xgeq -frac end right. $

Решением системы является луч (0,5;∞).

Ответ: $xin (0,5;infty )$

Если модуль больше выражения, то здесь иной равносильный переход.

$leftvert f(x)rightvert >g(x)leftrightarrow left< begin f(x)>g(x) \ f(x) &lt -g(x) end right. $

$leftvert f(x)rightvert geq g(x)leftrightarrow left< begin f(x)geq g(x) \ f(x)leq -g(x) end right. $

Другими словами, мы рассматриваем два случая: 1) сначала просто игнорируем модуль — решаем обычное неравенство; 2) затем по сути раскрываем модуль со знаком «минус», а затем умножаем обе части неравенства на −1, меня при этом знак. При этом варианты объединены квадратной скобкой, т.е. перед нами совокупность двух требований.

Пример. Решите неравенство

$leftvert x-7rightvert >8x$

Воспользуемся равносильным переходом.

$left[ begin x-7>8x \ x-7 &lt -8x end right. leftrightarrow left[ begin x-7-8x>0 \ x-7+8x &lt 0 end right. leftrightarrow left[ begin -7x>7 \ 9x &lt 7 endright. leftrightarrow left[ begin x &lt 1 \ x &lt frac end right. $

Решением совокупности является луч (-∞;1).

Ответ: $xin (-infty ;1)$

Пример. Решите неравенство

$leftvert 2x+8rightvert geq x-5$

Воспользуемся равносильным переходом.

$left[ begin 2x+8geq x-5 \ 2x+8leq -(x-5) end right. leftrightarrow left[ begin 2x-xgeq -5-8 \ 2x+xleq 5-8 end right. leftrightarrow left[ begin 2x-xgeq -5-8 \ 2x+xleq 5-8 end right. leftrightarrow left[ begin xgeq -13 \ 3xleq -3 end right. leftrightarrow left[ begin xgeq -13 \ xleq -1 end right. $

Решением совокупности является луч все множество действительных значений

Ответ: $xin (-infty ;infty )$

5. Метод расщепления неравенств

Ключевой момент в решении неравенства – преобразование его к виду, в котором левая часть представляет собой произведение каких-либо функций, а правая – равна нулю. Дробно-рациональные неравенства $frac

vee 0$ можно привести к равносильной системе:

$fracgeq 0leftrightarrow left[ begin left< begin f(x)geq 0 \ g(x)>0 end right. \ left< begin f(x)leq 0 \ g(x) &lt 0 end right. endright. $

$fracleq 0leftrightarrow left[ begin left< begin f(x)leq 0 \ g(x)>0 end right. \ left< begin f(x)geq 0 \ g(x) &lt 0 end right. end right. $

То есть иными словами, дробь положительна, когда числитель и знаменатель одного знака; дробь отрицательна, когда числитель и знаменатель разных знаков.

Произведение двух множителей равносильно совокупности систем:

$f(x)cdot g(x)geq 0leftrightarrow left[ begin left< begin f(x)geq 0 \ g(x)geq 0 end right. \ left< begin f(x) leq 0 \ g(x)leq 0end right. end right. $

$f(x)cdot g(x)leq 0leftrightarrow left[ begin left< begin f(x)leq 0 \ g(x)geq 0 end right. \ left< begin f(x)geq 0 \ g(x)leq 0 end right. end right. $

То есть иными словами, произведение двух множителей положительно, когда оба множителя одного знака; произведение отрицательно, когда оба множителя разных знаков.

Пример. Решите неравенство $fracgeq 0$

Решение. Воспользуемся равносильным переходом.

$left[ begin left< begin x-15geq 0 \ x-4>0 end right. \ left< begin x-15leq 0 \ x-4 &lt 0 end right. end right. leftrightarrow left[ begin left< begin xgeq 15 \ x>4 end right. \ left< begin xleq 15 \ x &lt 4 end right. end right. $

Решение первой системы – луч [15;∞)

Решение второй системы – открытый луч (-∞;4).

Значит, решением совокупности является объединение полученных решений, т.е. $xin (-infty ;4)cup lbrack 15;infty )$

Ответ: $xin (-infty ;4)cup lbrack 15;infty )$

Пример. Решите неравенство $fracleq 0$

Решение. Воспользуемся равносильным переходом.

$left[ begin left< begin 2x-3leq 0 \ x-1>0 end right. \ begin 2x-3geq 0 \ x-1 &lt 0 end end right. leftrightarrow left[ begin left< begin 2xleq 3 \ x>1 end right. \ begin 2xgeq 3 \ x &lt 1 end end right. leftrightarrow left[ begin left< begin xleq 1,5 \ x>1 end right. \ begin xgeq 1,5 \ x &lt 1 end end right. $

Решение первой системы – полуинтервал (1;1,5]

Вторая система не имеет решений.

Значит, решением совокупности является $xin (1;1,5]$