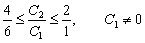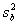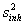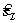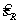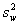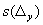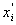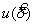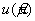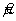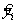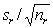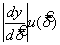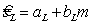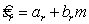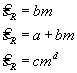Модель линейного программирования является как бы «моментальным снимком» реальной ситуации, когда параметры модели (коэффициенты целевой функции и неравенств ограничений) предполагаются неизменными. Естественно изучить влияние изменения параметров модели на полученное оптимальное решение задачи ЛП. Такое исследование называется Анализом на чувствительность. В этом разделе анализ чувствительности основывается на графическом решении задачи ЛП.
Компания производит краску для внутренних и наружных работ из сырья двух типов: М1 и М2.
Необходимая информация представлена в следующей таблице:
На 1 тонну краски
Ежедневный
расход сырья
Для наружных работ
Для внутренних работ
Доход на тонну краски (тыс. дол.)
Отдел маркетинга компании ограничил ежедневное производство краски для внутренних работ до 2 т, а кроме того этот показатель не должен превышать более чем на тонну показатель выпуска краски для внешних работ.
Определить оптимальное соотношение между видами выпускаемой продукции для максимизации общего ежедневного дохода.
Составленная математическая модель задачи выглядит следующим образом:
Максимизировать Z(x) = 5X1 + 4X2
При выполнении ограничений
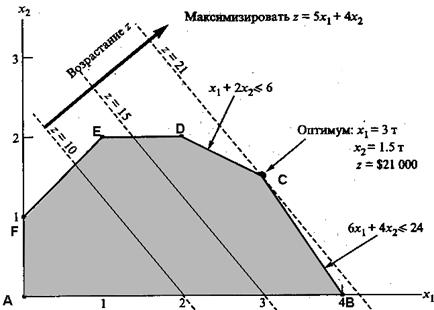
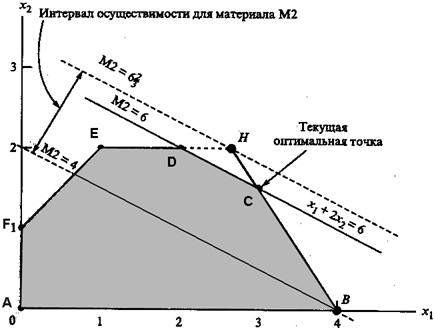
В результате применения графического метода решения ЗЛП, рассмотренного в параграфе 3.2, получен график (рис. 3.6).
Решением задачи является точка с координатами: Х1 = 3;Х2 = 1,5. Целевая функция при таком решении принимает значение Z = 21 тыс. дол.
Проведем для данной задачи анализ чувствительности. Рассмотрим два случая:
1) изменение коэффициентов целевой функции;
2) изменение значений констант в правой части неравенств-ограничений.
1. Изменение коэффициентов целевой функции. В общем виде целевую функцию задачи ЛП можно записать следующим образом:
Изменение значений коэффициентов С1 и С2 приводит к изменению угла наклона прямой Z. Графический способ решения показывает, что это может привести к изменению оптимального решения: оно будет достигаться в другой угловой точке пространства решений. Вместе с тем, очевидно, существуют интервалы изменения коэффициентов С1 и С2, когда текущее оптимальное решение сохраняется. Задача анализа чувствительности и состоит в получении такой информации. В частности, представляет интерес определение интервала оптимальности для отношения С1 /С2 (или, что то же самое, для С2 /С1); если значение отношения С1 /С2 не выходит за пределы этого интервала, то оптимальное решение в данной модели сохраняется неизменным.
На рис. 3.6 видно, что функция Z(x) = 5X1 + 4X2 достигает максимального значения в угловой точке С. При изменении коэффициентов целевой функции Z(x) = С1 X1 + C2 X2 точка С останется точкой оптимального решения до тех пор, пока угол наклона линии Z будет лежать между углами наклона двух прямых, пересечением которых является точка С. Этими прямыми являются 6Х1 + 4Х2 ≤ 24 (ограничение на сырье М1) и Х1 + 2Х2 ≤ 6 (ограничение на сырье М2). Алгебраически это можно записать следующим образом:
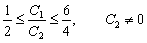
В первой системе неравенств условие 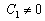
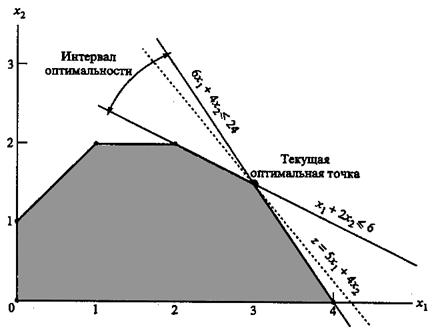
Рис. 3.7. Интервал оптимальности
Итак, если коэффициенты С1 и С2 удовлетворяют приведенным выше неравенствам, оптимальное решение по-прежнему будет достигаться в точке С. Отметим, если прямая Z(x) = С1 X1 + C2 X2 совпадет с прямой Х1 + 2Х2 ≤ 6, то оптимальным решением будет любая точка отрезка CD. Аналогично, если прямая, соответствующая целевой функции, совпадет с прямой 6Х1 + 4Х2 = 24, тогда любая точка отрезка ВС будет оптимальным решением. Однако очевидно, что в обоих случаях точка С остается точкой оптимального решения.
Приведенные выше неравенства можно использовать при определении интервала оптимальности для какого-либо одного коэффициента целевой функции, если предположить, что другой коэффициент остается неизменным. Например, зафиксируем значение коэффициента С2 (пусть С2 = 4), тогда интервал оптимальности для коэффициента С1 получаем из неравенств 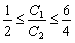
Это означает, что при фиксированной цене на краску для внутренних работ цена на краску для наружных работ может меняться в интервале от 2 тыс. дол. за тонну до 6 тыс. дол. за тонну, при том, что оптимальное соотношение (решение) останется неизменным.
Аналогично, если зафиксировать значение коэффициента С1 (пусть С1 = 5), тогда из неравенства 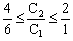
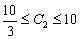
2. Изменение значений констант в правой части неравенств-ограничений. Стоимость ресурсов. Во многих моделях линейного программирования ограничения трактуются как условия ограниченности ресурсов. В таких ограничениях правая часть неравенств является верхней границей количества доступных ресурсов. Рассмотрим на примере чувствительность оптимального решения к изменению ограничений, накладываемых на ресурсы. Такой анализ задачи ЛП предлагает простую меру чувствительности решения, называемую Стоимостью единицы ресурса; при изменении количества доступных ресурсов (на единицу) значение целевой функции в оптимальном решении изменится на стоимость единицы ресурса.
В данной примере первые два неравенства представляют собой ограничения на использование сырья М1 и М2 соответственно. Определим стоимость единиц этих ресурсов.
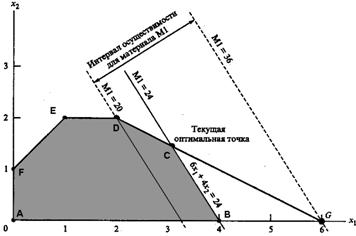
В данной задаче оптимальное решение достигается в точке С, являющейся точкой пересечения прямых, соответствующих ограничениям на сырье М1 и М2. При изменении уровня доступности материала М1 (увеличение или уменьшение текущего уровня, равного 24 т) точка С оптимального решения «плывет» вдоль отрезка DG (рис. 3.8).
Любое изменение уровня доступности материала М1, приводящее к выходу точки пересечения С из этого отрезка, ведет к неосуществимости оптимального решения в точке С. Поэтому можно сказать, что концевые точки D = (2,2) и G = (6,0) отрезка DG определяют Интервал осуществимости для ресурса М1. Количество сырья М1, соответствующего точке D = (2,2), равно 6Х1 + 4Х2 = 20 т. Аналогично, количество сырья, соответствующего точке G = (6,0), равно 36 т. Таким образом, интервал осуществимости для ресурса М1 составляет 20 ≤ М1 ≤ 36. Если определить М1 как М1 = 24 + D1, где D1 – отклонение количества материала М1 от текущего уровня в 24 т, тогда последние неравенства можно переписать как 20 ≤ 24 + D1 ≤ 36 или -4 ≤ D1 ≤ 12. Это означает, что текущий уровень ресурса М1 может быть уменьшен не более чем на 4 т и увеличен не более чем на 12 т. В этом случае структура оптимального решения не изменится.
Вычислим стоимость единицы материала М1. При изменении количества сырья М1 от 20 до 36 тонн, значения целевой функции Z будут соответствовать положению точки С на отрезке DG. Обозначив через y1 стоимость единицы ресурса М1, получим следующую формулу:
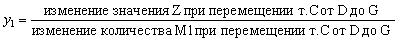
Если точка С совпадает с точкой D = (2,2), то Z = 5 ´ 2 + 4 ´ 2 = 18 (тыс. дол.), если же точка С совпадает с точкой G = (6,0), тогда Z = 5´6 + 4´0 = 30 (тыс. дол.). Отсюда следует, что
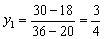
Этот результат показывает, что изменение количества ресурса М1 на одну тонну приводит к изменению в оптимальном решении значения целевой функции на 750 дол.
Рассмотрим ресурс М2. На рис. 3.9 видно, что интервал осуществимости для ресурса М2 определяется концевыми точками В и Н отрезка ВН, где В = (4,0) и Н = (8/3,2).
Точка Н находится на пересечении прямых ЕD и ВС. Находим, что количество сырья М2, соответствующего точке В, равно Х1 + 2Х2 = 4 + 2 ´ 0 = 4т, а в точке Н – 20/3 т. Значение целевой функции в точке В равно Z = 5 ´ 4 + 4 ´ 0 = 20 тыс. дол., а в точке Н: Z = 5 ´ ´ 8/3 + 4 ´ 2 = 64/3 тыс. дол. Отсюда следует, что количество сырья М2 может изменяться от 4 до 20/3 тонн, а стоимость единицы ресурса М2, обозначенная как y2, равна 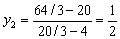
- Тема 8. Оценка неопределенности испытаний (стр. 1 )
- Тема 8. Оценка неопределенности испытаний.
- Вопросы:
- 1. Оценка неопределенности методом моделирования.
- Вопрос 1. Оценка неопределенности методом моделирования.
- Р 50.1.060-2006 Статистические методы. Руководство по использованию оценок повторяемости, воспроизводимости и правильности при оценке неопределенности измерений
- 1 Область применения
- 2 Нормативные ссылки
- 3 Термины и определения
- 4 Обозначения
- 5 Принципы
- 5.1 Отдельные результаты и свойства процесса измерений
- 5.2 Применение данных воспроизводимости
- 5.3. Основные уравнения статистической модели
- 5.4 Данные повторяемости
- 6 Оценка неопределенности с использованием оценок повторяемости, воспроизводимости и правильности
- 6.1 Процедура оценки неопределенности измерений
- 6.2 Различия между фактической прецизионностью и ее математическим ожиданием
- 7 Установление соответствия данных выполнения метода результатам измерений для конкретного процесса измерений
- 7.1 Общие положения
- 7.2 Демонстрация контролируемости лабораторной составляющей смещения
- 7.2.1 Общие требования
- 7.2.2 Методы демонстрации контролируемости лабораторной составляющей смещения.
- 7.2.3 Выявление существенной лабораторной составляющей смещения
- 7.3 Верификация повторяемости
- 7.4 Постоянная верификация
- 8 Учет особенностей объекта испытаний
- 8.1 Общие положения
- 8.2 Отбор выборки
- 8.2.1 Процесс отбора выборки
- 8.2.2 Негомогенность
- 8.3 Подготовка и предварительная обработка выборки
- 8.4 Изменение типа объекта испытаний
- 8.5 Изменение неопределенности в зависимости от уровня отклика
- 8.5.1 Корректировка sR
- 8.5.2 Изменение других вкладов в неопределенность
- 9 Дополнительные факторы
- 10 Общее выражение для суммарной стандартной неопределенности
- 11 Бюджет неопределенности, основанный на данных совместных исследований
- 12 Оценка неопределенности комбинированного результата
- 13 Представление информации о неопределенности
- 13.1 Общие положения
- 13.2 Выбор коэффициента охвата
- 13.2.1 Общие положения
- 13.2.2 Уровень доверия
- 13.2.3 Степени свободы, соответствующие оценке
- 14 Сравнение данных выполнения метода и неопределенности
- 14.1 Основные предположения
- 14.2 Процедура сравнения
- 14.3 Причины различий
- Приложение А (справочное) Подходы к оценке неопределенности
- Приложение В (справочное) Экспериментальная оценка неопределенности
- Приложение С (справочное) Примеры расчета неопределенности
Видео:Расстановка Коэффициентов в Химических Реакциях // Подготовка к ЕГЭ по ХимииСкачать

Тема 8. Оценка неопределенности испытаний (стр. 1 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 |
Видео:Как расставлять коэффициенты в уравнении реакции? Химия с нуля 7-8 класс | TutorOnlineСкачать

Тема 8. Оценка неопределенности испытаний.
Видео:Оценка неопределенности измеренийСкачать

Вопросы:
Видео:Расстановка коэффициентов в химических реакциях: как просто это сделатьСкачать

1. Оценка неопределенности методом моделирования.
2. Источники неопределенности.
3. Эмпирический метод оценки неопределенности.
Видео:Математика без Ху!ни. Метод неопределенных коэффициентов.Скачать

Вопрос 1. Оценка неопределенности методом моделирования.
В настоящее время выделяют три надежных способа (подхода) по количественной оценке неопределенности измерения:
1. Метод моделирования, изложенный в GUM, с применением закона распределения неопределенности;
2. Метод моделирования Монте-Карло (Приложения 1 к GUM);
3. Эмпирические методы, основанные на внутрилабораторном или межлабораторном исследовании выполнения методов измерений (испытаний).
Метод моделирования является наиболее разработанным и широко используемым для оценки неопределенности измерений.
Метод состоит в установлении модели измерений, которая связывает измеряемую величину с влияющими величинами, расчете стандартной неопределенности каждой влияющей величины и оценке, с учетом коэффициентов чувствительности, стандартной неопределенности измеряемой величины. При использовании этого метода предполагается, что поправки на значимые систематические эффекты включены в модель. Применение закона распространения неопределенности дает возможность оценить суммарную неопределенность, связанную с результатом. Подход зависит от частных производных для каждой влияющей величины, следовательно, зависит от вида функциональной зависимости результата или, если формой является алгоритм, от численного дифференцирования.
Типичными выходными данными подхода моделирования является «бюджет неопределенности», дающий итоговую оценку суммарной стандартной неопределенности результата измерения из неопределенностей входных величин. Бюджет неопределенности включает данные о каждой «входной величине» и ее вкладе в результат измерения и неопределенность и сами данные о результате измерения и ее неопределенности как показано ниже на схеме (рис. 3).
Бюджет неопределенности относится к определенному результату измерения. Однако, разработанный алгоритм бюджета неопределенности, обычно изложенный в методике расчета неопределенности, можно применить ко всем измерениям, проведенным с использованием того же метода. Для любого нового измерения (суммарная) стандартная неопределенность u(y) получается через введение в алгоритм входных данных xi и u(xi) для этого измерения, на основании которых затем будут получены y и u(y).
стандартная неопределенность u(xi)
(суммарная) стандартная неопределенность u(y)
коэффициент охвата k
вклад в неопределенность
расширенная неопределенность
U(y) = k·u(y)
Рис.3. Элементы бюджета неопределенности
Так как бюджет неопределенности содержит информацию об относительных величинах вкладов различных входных величин в неопределенность, то эта информация может быть использована для улучшения методики измерения и повышения ее точности.
Процесс оценивания неопределенности по методу моделирования состоит из следующих этапов.
1. Описание измерения, составление его модели и выявление источников неопределенности.
Любой процесс измерения можно представить в виде последовательности выполняемых операций. Поэтому для описания измеряемой величины и выявления источников неопределенности целесообразно представить цепь преобразования измеряемой величины в виде схемы, отображающей последовательность процесса измерений.
В большинстве случаев измеряемая величина Y не является прямо измеряемой, а зависит от N других измеряемых величин Х1, Х2 … ХN и выражается через функциональную зависимость

Y – выходная величина.
Входные величины X1, X2, … XN, от которых зависит выходная величина Y, являются непосредственно измеряемыми величинами и сами могут зависеть от других величин, включая поправки и поправочные коэффициенты на систематические эффекты:


Описание измеряемой величины в виде функциональной зависимости (математической модели), связывающей измеряемую величину с параметрами, от которых она зависит, называется моделированием.
Стадия моделирования является чрезвычайно важной, так как от правильности и тщательности составления модели измерения, которая определяется необходимой точностью, зависит количество источников неопределенности.
С целью обобщения источников неопределенности измеряемую (выходную) величину и выявленные источники неопределенности: входные величины и величины, на них влияющие целесообразно представить на диаграмме «причина – следствие» (рис. 4):
Рис. 4. Диаграмма «причина-следствие»
Источниками неопределенности могут быть пробоотбор, условия хранения, аппаратурные эффекты, чистота реактивов, условия измерений, влияние пробы, вычислительные и случайные эффекты, влияние оператора.
2.Оценивание значений и стандартных неопределенностей входных величин. Следующим этапом после выявления источников неопределенности является количественное описание неопределенностей, возникающих от этих источников. Это может быть сделано двумя путями:
– оцениванием неопределенности, возникающей от каждого отдельного источника с последующим суммированием составляющих;
– непосредственным определением суммарного вклада в неопределенность от некоторых или всех источников с использованием данных внутрилабораторных или межлабораторных исследований об эффективности метода в целом.
Для каждой входной величины необходимо определить оценку и стандартную неопределенность. При этом все входные величины вследствие того, что их значения не могут быть точно известны, являются случайными непрерывными. Тогда оценками входных величин (x1, x2 … xN), обозначаемыми малыми буквами, являются их математические ожидания, а стандартными неопределенностями u(xi) входных величин – стандартные отклонения. Оценку входных величин 
Оценивание неопределенности от каждого источника возможно двумя способами: по типу А (путем статистического анализа ряда наблюдений) и по типу В (иным способом, чем статистический анализ ряда наблюдений).
Исходными данными для оценивания стандартной неопределенности по типу А являются результаты многократных измерений xi1, … xim; i=1, …, m. На основании полученных результатов рассчитывается среднее арифметическое 

Стандартная неопределенность, связанная с оценкой 
Стандартная неопределенность u(xi) вычисляется по формуле:

для результата измерения 
Исходными данными для оценивания стандартной неопределенности по типу В является следующая априорная информация:
– данные предшествовавших измерений величин, входящих в уравнение измерения;
– сведения о виде распределения вероятностей;
– данные, основанные на опыте исследователя или общих знаниях о поведении и свойствах соответствующих средств измерений и материалов;
– неопределенности констант и справочных данных;
– данные поверки, калибровки, сведения изготовителя о средстве измерения и др.
Если оценка xi берется из спецификации изготовителя, свидетельства о поверке, справочника или другого источника, то неопределенность обычно дается как интервал ±a отклонения входной величины от ее оценки. Имеющуюся информацию о величинах xi необходимо правильно описать с помощью функции распределения вероятностей. Для определения стандартной неопределенности входных величин необходимо воспользоваться законом распределения вероятностей xi. При этом чаще всего используют следующие основные законы распределения:
Формулы и способы применения представлены в таблице 2.
Формулы расчета стандартной неопределенности
Видео:Метод неопределенных коэффициентовСкачать

Р 50.1.060-2006 Статистические методы. Руководство по использованию оценок повторяемости, воспроизводимости и правильности при оценке неопределенности измерений
ФЕДЕРАЛЬНОЕ АГЕНТСТВО
ПО ТЕХНИЧЕСКОМУ РЕГУЛИРОВАНИЮ И МЕТРОЛОГИИ
РЕКОМЕНДАЦИИ
ПО СТАНДАРТИЗАЦИИ
РУКОВОДСТВО ПО ИСПОЛЬЗОВАНИЮ ОЦЕНОК ПОВТОРЯЕМОСТИ, ВОСПРОИЗВОДИМОСТИ И ПРАВИЛЬНОСТИ ПРИ ОЦЕНКЕ НЕОПРЕДЕЛЕННОСТИ ИЗМЕРЕНИЙ
Москва
Стандартинформ
2007
Цели и принципы стандартизации в Российской Федерации установлены Федеральным законом от 27 декабря 2002 г. № 184-ФЗ «О техническом регулировании», а правила применения национальных стандартов Российской Федерации — ГОСТ Р 1.0-2004 «Стандартизация в Российской Федерации. Основные положения»
Сведения о рекомендациях по стандартизации
1 ПОДГОТОВЛЕНЫ Открытым акционерным обществом «Научно-исследовательский центр контроля и диагностики технических систем» (ОАО НИЦ КД) и Техническим комитетом по стандартизации ТК 125 «Статистические методы в управлении качеством продукции» на основе собственного аутентичного перевода стандарта, указанного в пункте 4
2 ВНЕСЕНЫ Управлением развития, информационного обеспечения и аккредитации Федерального агентства по техническому регулированию и метрологии
3 УТВЕРЖДЕНЫ И ВВЕДЕНЫ В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 19 декабря 2006 г. № 319-ст 4
4 Настоящие рекомендации являются идентичными по отношению к международному стандарту ИСО/ТУ 21748:2004 «Руководство по использованию оценок повторяемости, воспроизводимости и правильности при оценке неопределенности измерений» (ISO/TS 21748:2004 «Guidance for the use of repeatability, reproducibility and trueness estimates in measurement uncertainty estimation»).
Наименование настоящих рекомендаций изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2004 (подраздел 3.5).
При применении настоящих рекомендаций рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты, сведения о которых приведены в дополнительном приложении А
5 ВВЕДЕНЫ ВПЕРВЫЕ
1 Область применения
2 Нормативные ссылки
3 Термины и определения
5.1 Отдельные результаты и свойства процесса измерений
5.2 Применение данных воспроизводимости
5.3. Основные уравнения статистической модели
5.4 Данные повторяемости
6 Оценка неопределенности с использованием оценок повторяемости, воспроизводимости и правильности
6.1 Процедура оценки неопределенности измерений
6.2 Различия между фактической прецизионностью и ее математическим ожиданием
7 Установление соответствия данных выполнения метода результатам измерений для конкретного процесса измерений
7.1 Общие положения
7.2 Демонстрация контролируемости лабораторной составляющей смещения
7.2.1 Общие требования
7.2.2 Методы демонстрации контролируемости лабораторной составляющей смещения.
7.2.3 Выявление существенной лабораторной составляющей смещения
7.3 Верификация повторяемости
7.4 Постоянная верификация
8 Учет особенностей объекта испытаний
8.1 Общие положения
8.2 Отбор выборки
8.2.1 Процесс отбора выборки
8.3 Подготовка и предварительная обработка выборки
8.4 Изменение типа объекта испытаний
8.5 Изменение неопределенности в зависимости от уровня отклика
8.5.2 Изменение других вкладов в неопределенность
9 Дополнительные факторы
10 Общее выражение для суммарной стандартной неопределенности
11 Бюджет неопределенности, основанный на данных совместных исследований
12 Оценка неопределенности комбинированного результата
13 Представление информации о неопределенности
13.1 Общие положения
13.2 Выбор коэффициента охвата
13.2.1 Общие положения
13.2.2 Уровень доверия
13.2.3 Степени свободы, соответствующие оценке
14 Сравнение данных выполнения метода и неопределенности
14.1 Основные предположения
14.2 Процедура сравнения
14.3 Причины различий
Приложение А (справочное) Подходы к оценке неопределенности
Приложение В (справочное) Экспериментальная оценка неопределенности
Приложение С (справочное) Примеры расчета неопределенности
Приложение D (справочное) Сведения о соответствии ссылочных международных стандартов национальным стандартам Российской Федерации
Знание неопределенности, связанной с результатами измерений, является важным для интерпретации результатов. Без количественных оценок неопределенности невозможно решить, превышают ли наблюдаемые отклонения результатов экспериментальную изменчивость, соответствуют ли объекты испытаний установленным требованиям. Без информации о неопределенности существует риск неверного толкования результатов, а неправильные решения могут привести к ненужным расходам при производстве, неправильным судебным выводам, неблагоприятным последствиям для здоровья или неблагоприятным социальным последствиям.
Лаборатории, аккредитованные в соответствии с ИСО/МЭК 17025:2005 «Общие требования к компетентности испытательных и поверочных лабораторий», обязаны оценивать неопределенность результатов измерений и испытаний и составлять соответствующий отчет. Руководство GUM ( Guide to the expression of uncertainty in measurement ), изданное ИСО, основано на принятом стандартном подходе. Однако оно относится к ситуации, когда известна модель процесса измерений. Очень широкий диапазон стандартных методов испытаний может быть подвергнут совместному исследованию в соответствии с ИСО 5725-2:1994, Настоящие рекомендации устанавливают соответствующие методы оценки неопределенности результатов измерений и испытаний, основанные на принципах GUM при анализе общих данных.
Общий подход, используемый в настоящих рекомендациях, требует, чтобы:
— оценки повторяемости, воспроизводимости и правильности метода, полученные при совместном исследовании в соответствии с ИСО 5725-2:1994, могли быть получены по опубликованной информации об использовании метода испытаний. Эти оценки позволяют получать внутрилабораторные и межлабораторные составляющие неопределенности, а также оценку неопределенности результатов, связанную с правильностью метода;
— лаборатория подтвердила на основе проверок присущих ей смещения и прецизионности, что выполнение ею метода испытаний совместимо с установленными требованиями к методу испытаний. Это подтверждает, что опубликованные данные согласуются с результатами измерений и испытаний, полученными лабораторией;
— любые влияния на результаты измерений, которые не охвачены совместными исследованиями, были идентифицированы, а отклонения, вызванные этими воздействиями, определены количественно.
Оценку неопределенности определяют объединением оценок дисперсии, полученных в соответствии с GUM .
Для контроля полного понимания метода разброс результатов, полученных в совместном исследовании, часто полезно сравнивать с оценками неопределенности измерений, полученными с использованием процедур GUM . Такие сравнения будут более эффективны при использовании последовательных оценок одного и того же параметра, полученных на основе данных совместных исследований.
РЕКОМЕНДАЦИИ ПО СТАНДАРТИЗАЦИИ
РУКОВОДСТВО ПО ИСПОЛЬЗОВАНИЮ ОЦЕНОК ПОВТОРЯЕМОСТИ, ВОСПРОИЗВОДИМОСТИ И ПРАВИЛЬНОСТИ ПРИ ОЦЕНКЕ НЕОПРЕДЕЛЕННОСТИ ИЗМЕРЕНИЙ
Statistical methods.
Guidance for the use of repeatability, reproducibility and trueness estimates in measurement uncertainty estimation
Дата введения — 2007-06-01
Видео:Метод неопределенных коэффициентов. 10 класс.Скачать

1 Область применения
Настоящие рекомендации дают руководство для:
— оценки неопределенности измерений на основе данных, полученных в результате исследований, проводимых в соответствии с ИСО 5725-2;
— сравнения результатов совместного исследования с неопределенностью измерений, полученной с использованием формальных принципов переноса неопределенности (см. раздел 14).
ИСО 5725-3 устанавливает дополнительные модели для анализа промежуточной прецизионности. Однако, хотя этот общий подход может быть применен к использованию расширенных моделей, оценка неопределенности с использованием этих моделей не включена в настоящие рекомендации.
Настоящие рекомендации применимы во всех областях измерений и испытаний, когда должна быть определена неопределенность результатов.
Настоящие рекомендации не описывают применение данных повторяемости в отсутствие данных воспроизводимости.
Настоящие рекомендации предполагают, что признанные значимыми систематические воздействия устранены или путем численной корректировки, включенной в метод измерений, или путем анализа и устранения причины воздействий.
Настоящие рекомендации содержат общее руководство. Представленный подход к оценке неопределенности применим для многих целей, однако возможно применение других подходящих методов.
В общем случае информация, приведенная в настоящих рекомендациях, относительно результатов, методов и процессов измерений относится также к результатам, методам и процессам испытаний.
Видео:USMLE Step 1 - Диагностические тесты: чувствительность и специфичностьСкачать

2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие стандарты:
ИСО Руководство 33:2000 Использование стандартных образцов
ИСО/МЭК Руководство 43-1:1997 Проверка компетентности путем межлабораторных сравнений. Часть 1. Разработка и применение программ проверок компетентности лабораторий
ИСО 3534-1:1993 Статистика. Словарь и условные обозначения. Часть 1. Вероятность и основные статистические термины
ИСО 5725-1:1994 Точность (правильность и прецизионность) методов и результатов измерений. Часть 1. Основные положения и определения
ИСО 5725-2:1994 Точность (правильность и прецизионность) методов и результатов измерений. Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерений
ИСО 5725-3:1994 Точность (правильность и прецизионность) методов и результатов измерений. Часть 3. Промежуточные показатели прецизионности стандартного метода измерений
ИСО 5725-4:1994 Точность (правильность и прецизионность) методов и результатов измерений. Часть 4. Основные методы определения правильности стандартного метода измерений
ИСО 5725-5:1998 Точность (правильность и прецизионность) методов и результатов измерений. Часть 5. Альтернативные методы определения прецизионности стандартного метода измерений
ИСО 5725-6:1994 Точность (правильность и прецизионность) методов и результатов измерений. Часть 6. Использование значений точности на практике
ИСО/ТО 7871:1997 Контрольные карты кумулятивных сумм. Руководство по управлению качеством и анализу данных с помощью метода кумулятивных сумм
ИСО 8258:1991 Контрольные карты Шухарта
ИСО 10576-1:2003 Руководство по оценке соответствия установленным требованиям. Часть 1. Общие принципы
ИСО 11648-1:2003 Статистические аспекты выборочного контроля нештучной продукции. Часть 1. Общие принципы
Видео:Урок 100 (осн). Коэффициенты линейного и объемного расширения телСкачать

3 Термины и определения
В настоящем стандарте применены термины по ИСО 5725-3, а также следующие термины с соответствующими определениями:
3.1 смещение ( bias ): Разность между математическим ожиданием результатов наблюдений 1) и принятым опорным значением.
Примечание — Смещение — общая систематическая ошибка 2) в противоположность случайной ошибке. Может быть один или более компонентов, образующих систематическую ошибку. Большее систематическое смещение от принятого значения соответствует большему значению смещения.
1) Применительно к настоящим рекомендациям под наблюдениями следует понимать испытания и измерения.
2) Применительно к измерениям под ошибкой следует понимать «погрешность».
3.2 суммарная стандартная неопределенность ( combined standard uncertainty ) u (у) : Стандартная неопределенность результата измерений, полученного через значения нескольких других величин, равная положительному квадратному корню из суммы членов, представляющих собой дисперсии или ковариации этих других величин, взятых с весами, соответствующими степени влияния этих величин на результат измерений.
3.3 коэффициент охвата ( coverage factor ) к: Числовой коэффициент, используемый как множитель суммарной стандартной неопределенности при определении расширенной неопределенности.
Примечание — Коэффициент охвата к находится обычно в диапазоне от 2 до 3.
3.4 расширенная неопределенность ( expanded uncertainty ) U : Величина, определяемая интервалом вокруг математического ожидания результатов измерений, охватывающим большую долю распределения значений, которые обоснованно могут быть приписаны измеряемой величине.
1 Эта доля может быть определена через доверительную вероятность или уровень доверия интервала.
2 Чтобы связать определенный уровень доверия с интервалом расширенной неопределенности, необходимы предположения (в явной или неявной форме) о характере распределения вероятностей результатов измерений и их суммарной стандартной неопределенности. Уровень доверия, который соответствует этому интервалу, может соответствовать действительности только в той степени, в какой могут быть справедливы предположения.
3 Расширенную неопределенность называют полной неопределенностью в рекомендациях [2] INC-1 (1980).
3.5 прецизионность ( precision ): Близость между независимыми результатами наблюдений, полученными при определенных принятых условиях.
1 Прецизионность зависит от распределения случайных ошибок и не связана ни с истинным, ни с заданным значениями.
2 Меру прецизионности обычно выражают в терминах рассеяния и вычисляют как стандартное отклонение результатов наблюдений. Малой прецизионности соответствует большое стандартное отклонение.
3 Независимость результатов наблюдений означает, что результаты получены таким образом, что отсутствует влияние предыдущих результатов на том же самом или аналогичном объекте наблюдений. Количественные меры прецизионности решающим образом зависят от принятых условий. Условия повторяемости и условия воспроизводимости являются разными степенями принятых условий.
3.6 повторяемость ( repeatability ): Прецизионность в условиях повторяемости, то есть в условиях, когда независимые результаты наблюдений получены одним методом на идентичных объектах наблюдений в одной лаборатории одним и тем же оператором с использованием одного оборудования и за короткий интервал времени.
3.7 стандартное отклонение повторяемости ( repeatability standard deviation ): Стандартное отклонение результатов наблюдений, полученных в условиях повторяемости.
1 Это мера рассеяния результатов наблюдений в условиях повторяемости.
2 Аналогично «дисперсию повторяемости» и «коэффициент вариации повторяемости» надо определять как меры рассеяния результатов наблюдений в условиях повторяемости.
3.8 воспроизводимость ( reproducibility ): Прецизионность в условиях воспроизводимости, то есть в условиях, когда результаты наблюдений получены одним методом на идентичных объектах наблюдений в различных лабораториях с разными операторами с использованием различного оборудования.
Примечание — Для обоснованного заявления воспроизводимости необходимые требования на изменения условий. Воспроизводимость представляют количественно через дисперсию результатов.
3.9 стандартное отклонение воспроизводимости ( reproducibility standard deviation ): Стандартное отклонение результатов наблюдений, полученных в условиях воспроизводимости.
1 Это мера рассеяния распределения результатов наблюдений в условиях воспроизводимости.
2 Аналогично «дисперсию воспроизводимости» и «коэффициент вариации воспроизводимости» надо определять как меры рассеяния результатов наблюдений в условиях воспроизводимости.
3.10 стандартная неопределенность ( standard uncertainty ) u (х i ) : Неопределенность результатов измерений, выраженная в виде стандартного отклонения.
3.11 правильность ( trueness ): Близость среднего значения, полученного на основании серии результатов наблюдений, к принятому опорному значению.
Примечание — Меру правильности обычно выражают в терминах смещения. Ссылка на правильность как «точность среднего» не рекомендуется.
3.12 неопределенность (измерения) ( uncertainty ): Параметр, связанный с результатом измерений, характеризующий рассеяние значений, которые обоснованно могут быть приписаны измеряемой величине.
1 Параметром может быть, например, стандартное отклонение (или величина, кратная ему) или полуширина интервала, имеющего установленный уровень доверия.
2 Неопределенность измерений включает в себя в общем случае несколько составляющих. Некоторые из этих составляющих могут быть оценены по статистическим распределениям результатов серии измерений и охарактеризованы экспериментальным стандартным отклонением. Другие составляющие, которые также могут быть охарактеризованы стандартными отклонениями, оцениваются на основе предположений о распределении вероятностей, основанных на экспериментальной или другой информации.
3 Понятно, что результат измерений является лучшей оценкой измеряемой величины, а все составляющие неопределенности, включая те, которые являются результатом систематических воздействий, таких как поправки корректировки и эталоны, вносят свой вклад в рассеяние результатов.
3.13 бюджет неопределенности ( uncertainty budget ): Список источников неопределенности с соответствующими им стандартными неопределенностями, собранный для определения суммарной стандартной неопределенности результата измерений.
Примечание — Список часто включает в себя дополнительную информацию, такую как коэффициент чувствительности (интенсивность изменения результатов в зависимости от величины воздействия на результат), степени свободы для каждой стандартной неопределенности и идентификацию средних, соответствующих каждой стандартной неопределенности, в терминах оценок типа А или типа В.
Видео:Чувствительность и специфичность тестаСкачать

4 Обозначения
— коэффициент, указывающий отрезок, отсекаемый прямой на оси абсцисс в эмпирической функции 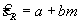
— лабораторная составляющая смещения;
— коэффициент наклона прямой в эмпирической функции 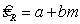
— коэффициент в эмпирической функции 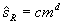
— коэффициент чувствительности 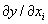
— коэффициент показателя степени в эмпирической функции 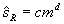
— случайная погрешность результата измерений (остаточная ошибка);
— случайная погрешность результата измерений (остаточная ошибка) в условиях повторяемости;
— числовой коэффициент, используемый как множитель суммарной стандартной неопределенности u при определении расширенной неопределенности U ;
— среднее измеряемой величины;
— количество составляющих, используемых в вычислениях неопределенности;
— количество объединяемых составляющих при вычислении суммарной неопределенности в дополнение к совместно исследуемым данным;
— количество повторений на одном уровне лабораторией l ;
— количество повторений измерения;
— количество объектов испытаний из большей (по количеству) партии;
— количество назначенных величин в соответствии с соглашением в процесс совместных исследований;
— коэффициент корреляции xi и xj (изменяется от — 1 до + 1);
— стандартное отклонение, представляющее межгрупповую составляющую дисперсии;
— межгрупповая составляющая дисперсии;
— оценочное или экспериментальное стандартное отклонение результатов наблюдений, полученных повторными измерениями на образце сравнения, используемом при контроле смещения;
— стандартное отклонение повторяемости c 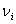
— неопределенность, соответствующая неоднородности образца;
— составляющая дисперсии, соответствующая неоднородности образца;
— экспериментальное или оценочное межлабораторное стандартное отклонение;
— скорректированная неопределенность, соответствующая В, когда вклад зависит от выходной переменной;
— оцениваемая дисперсия В;
— внутрилабораторное стандартное отклонение;
— скорректированная оценка внутрилабораторного стандартного отклонения, когда вклад зависит от выходной переменной;
— оцениваемая дисперсия er
— оцениваемое стандартное отклонение воспроизводимости;
— скорректированная оценка стандартного отклонения воспроизводимости;
— скорректированное стандартное отклонение воспроизводимости, вычисленное по эмпирической модели, когда вклады зависят от выходной переменной;
— внутрилабораторное стандартное отклонение, полученное из повторных измерений или других повторных исследований;
— внутригрупповая составляющая дисперсии (часто внутрилабораторная составляющая дисперсии);
— лабораторное стандартное отклонение разностей при сравнении обычного метода с точным методом;
— i -е исходное значение при определении результата;
— отклонение i -го исходного значения от номинального значения х;
— j -е исходное значение при определении результата;
— неопределенность, соответствующая δ, вызванная неопределенностью оценки δ, по измерениям исходного эталона или сравнения образца с сертифицированным значением 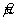
— неопределенность, соответствующая сертифицированному значению
— суммарная стандартная неопределенность, соответствующая y 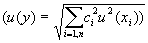
— суммарная неопределенность для результата Y = f ( y 1 , y 2 ,…) 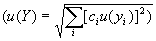
— суммарная стандартная неопределенность, соответствующая у, выраженная через дисперсию 3) ;
— неопределенность, соответствующая неоднородности выборки;
— расширенная неопределенность, равная стандартной неопределенности u , умноженной на k ;
— расширенная неопределенность у, когда U ( y ) = ku (у) ( k — коэффициент охвата);
— результат испытаний i -го объекта точного метода при сравнении методов;
— результат испытаний i -го объекта от обычного метода испытаний при сравнении методов;
— заданное значение для проверки квалификации;
— оценка смещения i -й лаборатории, равная среднему лаборатории m , минус сертифицированное значение 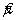
— среднее смещение лаборатории при сравнении обычного метода с фиксированным;
— смещение, соответствующее используемому методу измерений;
— оцененное или измеренное смещение;
— неизвестное математическое ожидание результата 4) ;
— сертифицированное значение образца сравнения;
— стандартное отклонение при проверке квалификации;
— истинное значение стандартного отклонения результатов, полученных повторными измерениями на образце сравнения, используемом для контроля смещения;
— межлабораторное стандартное отклонение; стандартное отклонение В;
— дисперсия B ; межлабораторная дисперсия;
— внутрилабораторное стандартное отклонение; стандартное отклонение е r ;
— дисперсия е r ; внутрилабораторная дисперсия;
— стандартное отклонение внутри группы;
— стандартное отклонение, требуемое для адекватной работы ИСО Руководство 33;
— эффективная степень свободы для стандартного отклонения или неопределенности, соответствующей входному значению х i ;
— число степеней свободы.
3) В соответствии с GUM [1] u 2 (у) — суммарная дисперсия, соответствующая оценке y выходной величины.
4) В соответствии с ГОСТ Р ИСО 5225.1 μ-истинное или принятое опорное значение измеряемой величины.
Видео:Метод неопределенных коэффициентовСкачать

5 Принципы
Видео:Расстановка коэффициентов в химических реакциях: как просто это сделатьСкачать
5.1 Отдельные результаты и свойства процесса измерений
5.1.1 Неопределенность измерений относят к отдельным результатам измерений. Повторяемость, воспроизводимость и правильность, напротив, относят к выполнению процесса измерений или испытаний. Для анализа в соответствии со всеми частями ИСО 5725 процесс измерений или испытаний является единым методом измерений, используемым всеми лабораториями, принимающими участие в исследовании. Следует заметить, что в настоящих рекомендациях под методом измерений понимают единственную детальную процедуру (как определено в Международном словаре основных и общих терминов в метрологии ( VIM ) [2] ). Неявно в настоящих рекомендациях предполагается, что графики, отражающие выполнение процесса, полученные при исследовании метода, соответствуют всем отдельным результатам измерений, полученным с помощью процесса. Это предположение требует подтверждающих доказательств в виде данных соответствующего контроля качества и уверенности в качестве процесса измерений ( раздел 7).
5.1.2 Ниже будет показано, что дополнительно может потребоваться учитывать различия между отдельными объектами испытаний. Однако в этом случае не нужно предпринимать индивидуальные и детальные исследования неопределенности для каждого объекта испытаний при наличии хорошо охарактеризованного и устойчивого процесса измерений.
Видео:Как расставить коэффициенты? Как превратить схему химической реакции в уравнение химической реакции.Скачать

5.2 Применение данных воспроизводимости
Применение данного документа основано на двух принципах:
— стандартное отклонение воспроизводимости, полученное при совместных исследованиях, является правомерной основой для оценки неопределенности измерений (см. 2.1);
— воздействия, не наблюдаемые в процессе совместных исследований, должны быть незначительными или явно учитываться. Последний принцип является расширением основной модели, используемой для совместных исследований (см. А.2.3).
Видео:Определение коэффициента вязкости жидкости. Проверка закона СтоксаСкачать

5.3. Основные уравнения статистической модели
5.3.1 Статистическая модель, на которой основано данное руководство, сформулирована в виде уравнения:
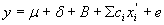
μ — неизвестное математическое ожидание;
δ — смещение, присущее методу измерений;
B — лабораторная составляющая смещения;
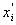
е — остаточная ошибка.
Предполагается, что B и е подчиняются нормальному распределению с нулевым средним и дисперсиями 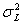
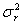
Так как наблюдаемые стандартные отклонения смещения метода δ, лабораторные смещения B и остаточные ошибки е являются полными мерами разброса в условиях совместного исследования, сумма 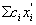
Примерами таких действий являются следующие:
а) подготовка объекта испытаний, выполняемая практически для каждого испытываемого объекта, но выполненная до совместных исследований;
b ) влияние подвыборки в случае, когда объекты, подвергаемые совместному исследованию, были гармонизированы до исследования. Предполагается, что 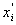
Пояснения для этой модели приведены в приложении А.
Примечание — Ошибка обычно определяется как разность между установленным значением и результатом измерений. В ( GUM [1] «ошибку» четко отличают от «неопределенности» (разброса значений). При оценке неопределенности, однако, важно характеризовать разброс значений, вызванный случайными воздействиями, и включать его в модель. Для представленных целей это достигается включением члена, характеризующего «ошибку» с нулевым математическим ожиданием, как в уравнении (1).
5.3.2 Учитывая модель, описываемую уравнением (1), неопределенность u (у) , связанную с наблюдениями, можно оценить, применяя уравнение:
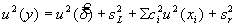
где 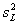
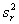
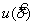
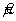
u ( xi ) — неопределенность, связанная с 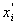
Учитывая, что стандартное отклонение воспроизводимости sR , задаваемое равенством, 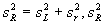
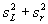
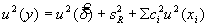
Видео:Андреев В.В. Чувствительность. Методика оценки.Скачать

5.4 Данные повторяемости
Данные повторяемости используют в настоящих рекомендациях прежде всего для проверки прецизионности, которая в соединении с другими тестами подтверждает, что конкретная лаборатория может применять данные воспроизводимости математического ожидания и правильности при оценке неопределенности. Данные повторяемости используют также при вычислении составляющей воспроизводимости в неопределенности (см. 7.3 и 11).
Видео:Метод неопределенных коэффициентовСкачать

6 Оценка неопределенности с использованием оценок повторяемости, воспроизводимости и правильности
Видео:Расстановка коэффициентов в окислительно-восстановительных реакцияхСкачать

6.1 Процедура оценки неопределенности измерений
Принципы, на которых основаны настоящие рекомендации (см. 5.1), приводят к следующей процедуре оценки неопределенности измерений:
а) получение оценок повторяемости, воспроизводимости и правильности метода на основе опубликованной информации о методе;
b ) проверка, не превышает ли лабораторное смещение, рассчитанное по измерениям на основе данных, полученных в соответствии с перечислением а);
с) проверка, не превышает ли прецизионность, полученная по текущим измерениям прецизионности, полученной на основе оценок повторяемости и воспроизводимости в соответствии с перечислением а);
d ) идентификация любых воздействий на измерение, которые не были учтены в процессе исследований в соответствии с перечислением а), и определение количественной оценки отклонения, которое может вызывать эти воздействия, учитывая коэффициент чувствительности и неопределенности каждого воздействия;
е) объединение оценки воспроизводимости (перечисление а)) с неопределенностью соответствующей правильности (перечисления а) и b)) и результатами дополнительных воздействий (перечисление d )) для формирования оценки суммарной неопределенности, когда смещение и прецизионность находятся под контролем в соответствии с перечислениями b ) и с).
Этапы этой процедуры описаны более подробно в разделах 7- 11.
Примечание — В рекомендациях предполагается, что в случае, когда смещение является неконтролируемым, выполняют корректирующие действия, чтобы привести процесс в управляющую зону.
Видео:46. Вычисление пределов с помощью эквивалентных бесконечно малых функцийСкачать

6.2 Различия между фактической прецизионностью и ее математическим ожиданием
Если фактическая прецизионность отличается от математического ожидания прецизионности, полученного на основе исследований в соответствии с перечислением а), соответствующие вклады в неопределенность должны быть учтены. В 8.5 описаны регуляторы оценок воспроизводимости для общего случая, когда прецизионность приближенно пропорциональна уровню отклика.
Видео:Погрешности измеренияСкачать

7 Установление соответствия данных выполнения метода результатам измерений для конкретного процесса измерений
7.1 Общие положения
Результатами совместного исследования являются sR , sr и, в некоторых случаях, оценка смещения метода, которые формируют требования для выполнения метода. При принятии метода для применения ожидается, что лаборатория продемонстрирует, что она выполняет эти требования. В большинстве случаев это достигается исследованиями, направленными на подтверждение контроля повторяемости (см. 7.3) и лабораторной составляющей смещения (см. 7.2), и постоянными проверками выполнения метода (контроль и обеспечение качества (см. 7.4)).
7.2 Демонстрация контролируемости лабораторной составляющей смещения
7.2.1 Общие требования
7.2.1.1 Лаборатория должна продемонстрировать, что ее смещение при выполнении метода находится под контролем, то есть лабораторная составляющая смещения не выходит за пределы смещения, полученного из совместных исследований. В следующих описаниях предполагается, что контроль смещения выполнен на материалах значениями, близкими к объектам исследования при обычных испытаниях. В тех случаях, когда материалы, используемые для проверки смещения, не имеют значений, близких к материалам, исследуемым при обычных испытаниях, итоговые вклады в неопределенность должны быть исправлены в соответствии с условиями 8.4 и 8.5.
7.2.1.2 В общем случае проверка лабораторной составляющей смещения сводится к сравнению лабораторных результатов с некоторыми эталонными значениями и представляет собой оценку В. Уравнение (2) показывает, что неопределенность, связанная с изменениями В, характеризуется sL , непосредственно входящей в sR . Однако, поскольку проверка смещения имеет собственную неопределенность, неопределенность сравнения в принципе увеличивает неопределенность результатов, получаемых при будущих применениях метода. По этой причине важно гарантировать, что неопределенность, связанная с проверкой смещения, мала по сравнению с sR (в идеале меньше, чем 0,2 sR ) и, следовательно, соответствующее увеличение неопределенности является незначительным. В этом случае, если свидетельства чрезмерной лабораторной составляющей смещения не обнаружены, уравнение (3) применяют без изменений. Если неопределенность, связанная с проверкой смещения, является большой, благоразумно увеличивать неопределенность, оцененную на основе уравнения (3) (см. 3.13). Если на основе совместных исследований правильности известно, что метод имеет незначительное смещение, известное смещение метода следует учитывать при оценке лабораторного смещения, например, путем исправления результатов на известное смещение метода.
7.2.2 Методы демонстрации контролируемости лабораторной составляющей смещения.
7.2.2.1 Общие положения
Контролируемость смещения может быть продемонстрирована одним из следующих методов. Последовательно одни и те же общие критерии используются для всех тестов на смещение, приведенных в настоящих рекомендациях, Допускается использовать более строгие тесты и проверки.
7.2.2.2 Исследование образца сравнения или эталона стандартного метода измерений Лаборатория l должна исполнить nl повторных измерений на исходном эталоне в условиях повторяемости, чтобы получить оценку смещения на этом веществе Δ l ; (равную среднему лаборатории m минус стандартное значение 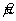
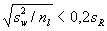
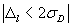
Заменив σ0 на его приближение sD в уравнении (4), получаем уравнение:
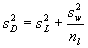
где nl — количество повторений лаборатории l ;
sw — внутрилабораторное стандартное отклонение, полученное на основе nl повторений или других исследований повторяемости;
sL — межлабораторное стандартное отклонение.
Соответствие критерию, описываемому уравнением (4), является подтверждением того, что лабораторная составляющая смещения B находится в интервале значений, установленном при совместных исследованиях. Следует обратить внимание на то, что образец сравнения или эталон используют здесь для независимой проверки или в качестве контрольного вещества, а не для калибровки.
1 Лаборатория может применять более строгий критерий, чем уравнение (4), используя коэффициент охвата менее 2 или выполняя альтернативный и более чувствительный тест на смещение.
2 Эти процедуры предполагают, что неопределенность, связанная с эталонным значением, мала по сравнению с σ D.
7.2.2.3 Сравнения с заданным методом испытаний, обладающим известной неопределенностью Лаборатория l должна проверить соответствующее количество nl объектов испытаний, применяя заданный метод испытаний и метод, использованный лабораторией, получив, таким образом, nl пар 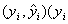
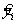
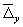
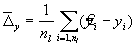
На практике значение nl должно быть выбрано так, чтобы неопределенность удовлетворяла неравенству 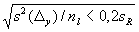
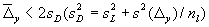
1 Лаборатория может выбирать более строгий критерий, чем уравнение (4), используя коэффициент охвата менее 2 или выполняя альтернативный и более чувствительный тест на смещение.
2 Эти процедуры предполагают, что неопределенность, связанная с эталонным методом, мала по сравнению с σ0.
7.2.2.4 Сравнение с другими лабораториями при использовании того же метода
Если лаборатория l участвует в дополнительных совместных исследованиях (например, при проверке квалификации в соответствии с ИСО/МЭК Руководство 43-1), для которых она может оценивать смещение, эти данные можно использовать для контроля смещения. Есть два возможных варианта:
а) при выполнении испытаний используют эталон или образец сравнения с независимо назначенными значениями неопределенности. Затем применяют процедуру 7.2.2.2 без изменений;
b ) проводят проверку соответствия q (≥1) заданных значений у1, у2, . у q Лаборатории, чьи результаты представлены значениями 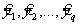
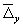
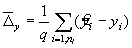
Процесс измерений удовлетворяет требованиям, если 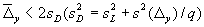
1 Эта процедура предполагает, что заданные значения основаны на количестве результатов, превышающем q, и обладают незначительной неопределенностью.
2 В некоторых схемах проверки квалификации все значения у i, преобразуют в z-множество zi = (у i–у0)/σ0 вычитанием заданного значения у0 и делением на стандартное отклонение σ0 (см. ИСО/МЭК Руководство 43-1). Если стандартное отклонение метода менее или равно sR, среднее z-множества лежит между 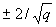
7.2.3 Выявление существенной лабораторной составляющей смещения
Как отмечено в разделе 1, настоящие рекомендации применимы только в тех случаях, когда лабораторная составляющая смещения находится под контролем. Если обнаружено чрезмерное смещение, предполагается, что будут предприняты действия для приведения смещения в границы требуемого диапазона до продолжения измерений. Такие действия обычно требуют проведения исследований и устранения причины смещения.
7.3 Верификация повторяемости
7.3.1 Испытательная лаборатория должна продемонстрировать, что ее повторяемость совместима со стандартным отклонением повторяемости, полученным при совместных исследованиях. Демонстрация достигается проведением анализа одного или более подходящих испытываемых материалов для получения (объединяя результаты при необходимости) стандартного отклонения повторяемости si vi степенями свободы. Значения si необходимо сравнивать, используя F -тест с 95 %-ным уровнем доверия, со стандартным отклонением повторяемости sr , полученным при совместных исследованиях. На практике для получения vi ≥ 15 следует выполнять достаточно повторений.
7.3.2 Если si значительно больше sr , лаборатория должна или идентифицировать и устранять соответствующие причины, или использовать si вместо sr во всех оценках неопределенности, рассчитанных с использованием настоящих рекомендаций. Следует обратить внимание, что это вызывает увеличение оценки стандартного отклонения повторяемости sr , так как 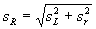
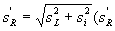
Наоборот, если si , значительно меньше sr , лаборатория может также использовать si , вместо sr , получая меньшую оценку неопределенности.
Во всех исследованиях прецизионности важно подтверждать, что данные свободны от неизвестных смещений, и проверять постоянство стандартного отклонения sw для различных объектов испытаний. Если стандартное отклонение sw непостоянно, может быть полезно оценить прецизионность отдельно для каждого различного класса объектов или построить общую модель (см. 8.5) для этой зависимости.
Примечание — Если требуется сравнение с заданным значением прецизионности, Руководство ИСО 33 более детально описывает соответствующий тест, основанный на 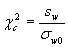
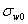
7.4 Постоянная верификация
Кроме предварительной оценки смещения и прецизионности, лаборатория должна принимать должные меры для гарантии того, что процедура измерений остается в состоянии статистического контроля. В частности, это включает следующее:
— соответствующий контроль качества, включая регулярные проверки смещения и прецизионности. Для этих проверок допускается использовать любые уместные устойчивые гомогенные объекты испытаний или материалы. Настоятельно рекомендуется использование контрольных карт (см. ИСО/ТО 7871 и ИСО 8258);
— меры по проверке качества, включая использование соответственно обученного и квалифицированного персонала, работающего в соответствующей системе качества.
8 Учет особенностей объекта испытаний
8.1 Общие положения
В совместных исследованиях или оценке промежуточных показателей прецизионности в соответствии с ИСО 5725-2 и ИСО 5725-3 обычно проводят измерения на гомогенных материалах или объектах небольшого количества типов. Это является обычной практикой для разделения подготовленных материалов. Однако объекты испытаний могут изменяться в широком диапазоне, что может требовать дополнительной обработки до испытаний. Например, образцы для экологических испытаний часто поставляют высушенными и гомогенизированными. Обычные образцы, как правило, являются влажными, неоднородными и грубо разделенными. Соответственно необходимо исследовать и, если необходимо, учитывать эти различия.
8.2 Отбор выборки
8.2.1 Процесс отбора выборки
Совместные исследования редко включают в себя этап отбора выборки. Если метод, использованный внутри лаборатории, включает в себя подвыборки или процедура оценивает свойство большого объема материала по маленькому образцу, то влияние отбора выборки необходимо исследовать. Может быть полезно обращаться к документации по отбору выборки, например к ИСО 11648-1 или другим стандартам.
8.2.2 Негомогенность
Негомогенность обычно исследуют экспериментально с применением дисперсионного анализа ( ANOVA ) 5) к нескольким объектам испытаний, для которых составляющая дисперсии 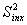
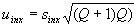
5) Принятая в международной практике аббревиатура для обозначения дисперсионного анализа ( Analysis of Variance).
8.3 Подготовка и предварительная обработка выборки
В большинстве исследований образцы являются гомогенными и могут быть дополнительно стабилизированы до распределения. Могут потребоваться исследования, позволяющие учитывать воздействия специфических процедур предварительной обработки внутри лаборатории. Как правило, такие исследования устанавливают воздействие этой процедуры на результаты измерений на исследуемых материалах с приблизительно или точно установленными свойствами. Воздействием может быть изменение разброса или систематических воздействий. Существенные изменения разброса следует устранять прибавлением соответствующей составляющей к бюджету неопределенности (предполагая, что воздействия увеличивают разброс). Если выявлены существенные систематические воздействия, наиболее удобно устанавливать соответствующий верхний предел. Следуя рекомендациям GUM [1] , этот предел можно рассматривать как границу прямоугольного или другого ограниченного симметричного распределения, а оценку стандартной неопределенности можно задавать в виде полуширины области изменений функции распределения, деленной на соответствующий коэффициент.
8.4 Изменение типа объекта испытаний
При необходимости следует исследовать неопределенность, являющуюся результатом изменения типа или состава объектов испытаний по сравнению с используемыми в совместных исследованиях. Как правило, подобные воздействия должны быть предсказаны на основе установленных воздействий, объемных свойств материала (которые дают оценку неопределенности, полученную в соответствии с GUM [1] ) или исследованы введением систематических или случайных изменений типа или состава объектов испытаний (см. приложение В).
8.5 Изменение неопределенности в зависимости от уровня отклика
8.5.1 Корректировка sR
Обычно некоторые или большая часть составляющих неопределенности измерений зависят от измеренного значения. ИСО 5725-2 рассматривает три простых случая, когда стандартное отклонение воспроизводимости для положительной величины m приближенно описывается одной из моделей
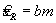
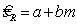
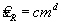
где 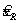
а, b , c и d — эмпирические коэффициенты, полученные на основе пяти или большего количества различных объектов испытаний с различными средними отклика m (а, b и c являются положительными).
При использовании уравнений (8)-(10) неопределенность должна основываться на оценке воспроизводимости, рассчитанной с использованием соответствующей модели.
В условиях 7.3 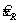
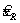
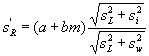
где 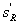
8.5.2 Изменение других вкладов в неопределенность
В общем случае, если любая составляющая неопределенности изменяется в соответствии с измеренным откликом предсказуемым способом, соответствующая стандартная неопределенность у должна быть откорректирована соответственно.
Примечание — Если вклады в неопределенность прямо пропорциональны у, часто бывает удобно выражать все существенные воздействия в терминах мультипликативных воздействий на у, а всю неопределенность — в форме относительных стандартных отклонений.
9 Дополнительные факторы
Раздел 8 рассматривает главные факторы, которые обычно различаются в совместных исследованиях и обычных испытаниях. Возможно, что в специфических случаях могут проявляться другие воздействия. Это может быть вызвано тем, что контролируемые переменные случайно или преднамеренно были постоянными в течение совместного исследования, или тем, что полный диапазон условий, достижимых в обычной практике, не был охвачен при совместных исследованиях.
Воздействия факторов, которые считаются постоянными или которые изменяются недостаточно при совместных исследованиях, следует оценивать отдельно либо в процессе экспериментального изменения, либо в соответствии с прогнозом на основе теории. В тех случаях, когда воздействия являются существенными, неопределенность, связанную с соответствующими факторами, необходимо оценивать, регистрировать и объединять с другими вкладами обычным способом (то есть суммировать в соответствии с уравнением (3)).
10 Общее выражение для суммарной стандартной неопределенности
Уравнение (3), при необходимости использовать скорректированную оценку 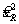
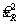
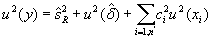
Значение 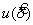
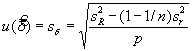
где p — количество лабораторий;
n — количество повторений в каждой лаборатории.
Переменная u ( B ) не использована в уравнении (12), потому что неопределенность sL , соответствующая B , уже включена в 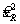
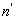
11 Бюджет неопределенности, основанный на данных совместных исследований
Настоящие рекомендации используют только одну приведенную в уравнении (3) модель для описания результатов измерений или испытаний. Информацию, подтверждающую справедливость модели, можно получать из различных источников, но если неопределенность, соответствующая испытаниям, остается незначительной, используют уравнение (3). Однако есть несколько различных ситуаций, при которых уравнение (3) немного изменяется. Например, если параметры воспроизводимости или повторяемости зависят от отклика. Бюджет неопределенности, если неопределенность совсем не зависит от отклика в исследуемом диапазоне, приведен в таблице 1, а для случая, когда неопределенность зависит от отклика, — в таблице 2.
Таблица 1 — Составляющие неопределенности, не зависящие от отклика
Стандартная неопределенность а , соответствующая у
Используют, если смещение, выявленное при совместных исследованиях, устранено, а неопределенность является существенной
Если среднее, полученное по nr полных повторений метода b , применяют к объекту испытаний, неопределенность, соответствующая е r , принимает вид —
См. Раздел 8 и приложение В
a Стандартная неопределенность измеряется в тех же единицах, что и у.
b Метод может включать nr повторений всего метода и любые предусмотренные повторения.
Таблица 2 — Составляющие неопределенности, зависящие от отклика
Стандартная неопределенность a, b , соответствующая у
Используют, только если выявленное при совместном исследовании смещение устранено, а неопределенность является существенной. (Производную используют, чтобы охватить случаи, когда устранение смещения не сводится к простому сложению или вычитанию)
aL и bL — коэффициенты предполагаемой линейной зависимости между sL и средним откликом m , аналогичной уравнению (9). Эта форма применима, только если установлена зависимость sL от m . В противном случае используют комбинированную оценку, соответствующую В и е r таблицы 1
ar и br — коэффициенты предполагаемой линейной зависимости между sr и средним откликом m , аналогичной уравнению (9). Если среднее, полученное по nr полных повторений метода, применяют к объекту испытаний, неопределенность, соответствующая е r , принимает вид — 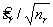
Эта форма применима, только если установлена зависимость sr от m . В противном случае используют объединенную оценку, соответствующую B и е r из таблицы 1
а и b — коэффициенты линейных отношений между sR и средним откликом m , как определено в уравнениях (9) и (10). Эту объединенную оценку следует использовать вместо отдельных оценок В и е r (см. таблицу 1), когда отдельные зависимости sL и sr от m не установлены
См. Раздел 8 и приложение В
а Стандартную неопределенность измеряют в тех же единицах, что и у.
b Предполагается простая линейная зависимость, соответствующая уравнению (9).
с Метод может включать nr повторений всего метода и любые предусмотренные повторения.
12 Оценка неопределенности комбинированного результата
12.1 Комбинированный результат формируют из совокупности результатов различных испытаний, каждый из которых охарактеризован совместными исследованиями. Например, вычисления по определению состава мяса обычно объединяют определением содержания белка (рассчитанного путем определения содержания азота), жира и влаги. При этом содержание каждого вещества определяют соответствующим стандартным методом.
12.2 Неопределенность u ( yi ) для каждого результата у, может быть получена на основе принципов, приведенных в настоящих рекомендациях, или непосредственно используя уравнения (1) или (2) соответственно. Если величины у i независимы, суммарную неопределенность u ( Y ) для результата Y = f ( y 1 , y 2 ,. ) вычисляют по формуле:
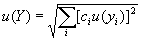
Если yi не являются независимыми, должны быть сделаны предположения относительно корреляции в соответствии с GUM [1] (также используют уравнение (А.2)).
13 Представление информации о неопределенности
13.1 Общие положения
Неопределенность может быть представлена в виде суммарной стандартной неопределенности u ( y ) или суммарной расширенной неопределенности U ( y ) = ku ( y ) ( k — коэффициент охвата) (см. 13.2 и GUM [1] ). Может быть удобно представить неопределенность в относительных величинах как коэффициент вариации или расширенную неопределенность, выражаемые в процентах зарегистрированных результатов.
13.2 Выбор коэффициента охвата
13.2.1 Общие положения
При оценке суммарной расширенной неопределенности применяют следующие исследования для выбора коэффициента охвата k .
13.2.2 Уровень доверия
Для практических целей должно быть указано значение суммарной расширенной неопределенности, соответствующее уровню доверия 95 %. Однако выбор уровня доверия зависит от диапазона факторов, таких как критичность и последствия применения неправильных результатов. Эти факторы вместе с любыми рекомендациями или юридическими требованиями, касающимися применения, должны быть рассмотрены при выборе k .
13.2.3 Степени свободы, соответствующие оценке
13.2.3.1 Для большинства практических целей, когда требуется 95 %-ный уровень доверия и число степеней свободы в доминирующих составляющих неопределенности превышает 10 (>10), выбор k = 2 обеспечивает достаточно надежный охват вероятного диапазона значений. Однако есть обстоятельства, в которых это приводит к существенной недооценке, особенно когда один или более значимых членов уравнения (12) имеют число степеней свободы менее 7.
13.2.3.2 Если один такой член ui ( y ) с vi ,- степенями свободы доминирует [признаком является выполнение неравенства ui ( y ) > 0,7 u ( y ) ], обычно достаточно взять в качестве vi эффективные степени свободы veff , соответствующие u ( y ) .
13.2.3.3 Если несколько существенных членов имеют приблизительно равную величину и степени свободы, удовлетворяющие условию vi 95 %) без хорошего знания распределения не рекомендуется.
14 Сравнение данных выполнения метода и неопределенности
14.1 Основные предположения
Оценка неопределенности измерений в соответствии с настоящими рекомендациями обеспечивает стандартную неопределенность, которая, хотя и основывается прежде всего на оценках воспроизводимости или промежуточной прецизионности, отдает должное факторам, которые не изменяются в процессе исследований, в которых эти оценки прецизионности получены. В принципе итоговая стандартная неопределенность u ( y ) должна быть идентична неопределенности, полученной на основе детальной математической модели процесса измерений. Сравнение этих двух оценок, если это возможно, обеспечивает полезную проверку качества оценки. Рекомендованная процедура описана в 14.2.
Процедура основана на двух важных предположениях:
— во-первых, оценку стандартной неопределенности u ( y ) с veff эффективными степенями свободы обычно определяют в предположении о нормальном распределении наблюдений (это означает, что ( n -1)( s 2 /σ 2 ) подчиняется χ 2 распределению с ( n -1) степенями свободы), Это предположение позволяет использовать F -критерий. Однако, поскольку суммарная неопределенность может включать неопределенность, связанную с величинами, описываемыми распределениями различной формы с различными дисперсиями, результаты испытаний необходимо рассматривать как индикатор, а уровень доверия следует выбирать с необходимой осторожностью;
— во-вторых, обычно предполагают, что две оценки неопределенности, которые будут сравниваться, полностью независимы. Это также маловероятно на практике, так как некоторые факторы могут быть общими для обеих оценок. Более тонкие воздействия являются предметом исследований для выявления влияния составляющей неопределенности, соответствующей выполнению работ в разных лабораториях. Предполагается, что приняты необходимые меры предосторожности, чтобы избежать этого воздействия. Если значимые факторы являются общими для обеих оценок неопределенности, очевидно, что оценки будут подобны значительно чаще, В этом случае, если последовательные испытания не в состоянии выявлять существенные различия, результаты не следует трактовать как свидетельство надежности модели измерений.
14.2 Процедура сравнения
Для сравнения двух оценок u ( y ) 1 и u ( y ) 2 ( u ( y ) 1 является большей из них) с эффективными степенями свободы v 1 и v 2 соответственно, используя уровень доверия α (например, для 95 %-ного уровня доверия α = 0,05), необходимо выполнить следующие действия:
найти по таблицам или получить с помощью программного обеспечения одностороннее верхнее критическое значение Fcrit = F (α/2, v 1 , v 2 ). Если даны верхнее и нижнее значения, выбирают верхнее значение, которое всегда больше 1;
14.3 Причины различий
Существует много причин для существенного различия между суммарными оценками неопределенности. Они включают в себя следующее:
— подлинные различия в работе лабораторий;
— неудачную модель, не учитывающую влияние всех существенных воздействий на измерения;
— неверную оценку значимого вклада в неопределенность.
Приложение А (справочное)
Подходы к оценке неопределенности
Руководство по оценке неопределенности измерений ( GUM [1] ), изданное ИСО, устанавливает методологию оценки неопределенности измерений, связанную с результатом y в соответствии с моделью процесса измерений. Методология GUM базируется на рекомендациях Международной палаты мер и весов ( BIPM [3], которые признают, что составляющие неопределенности можно оценивать либо на основе статистического анализа серии наблюдений (оценка типа А), либо другими средствами (оценка типа В), например, используя данные публикаций о неопределенности образцов сравнения или эталонов или, при необходимости, мнения специалистов. Отдельные составляющие выражают в виде стандартных отклонений и, при необходимости, затем объединяют.
Выполнение рекомендаций В I РМ [3] в GUM [1] начинается с модели измерений в виде функции у = f ( x 1 , х2, . , х N ), связывающей результат измерений у со входными величинами х i . Тогда в случае независимых входных величин GUM дает неопределенность u ( y ) в соответствии с уравнением (А.1):
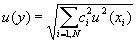
где с i — коэффициент чувствительности, оцениваемый в соответствии с уравнением с i = dy / dxi , (частная производная у по х i );
u ( xi ) и u ( y ) — стандартные неопределенности, то есть неопределенности измерений, выраженные в виде стандартных отклонений.
Если переменные не являются независимыми, выражение для неопределенности является более сложным и определяется уравнением:
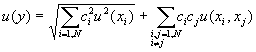
ci и cj — коэффициенты чувствительности, соответствующие уравнению (А.1). На практике часто ковариацию выражают через коэффициент корреляции rij :
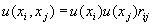
где — 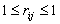
В случаях, учитывающих нелинейность модели измерений, уравнение (А.1) расширяют, включая члены более высокого порядка. Эта ситуация более подробно описана в GUM [1] . После вычисления комбинированной стандартной неопределенности с использованием уравнений (А.1)-(А.3) расширенную неопределенность определяют, умножая u ( y ) на коэффициент охвата k , который выбирают на основе числа степеней свободы для u ( y ) . Более подробно это описано в разделе 13.
В подходе GUM существует неявное предположение, что входные данные измерены или назначены. Если возникают воздействия, которые могут быть не определены через измеримые величины (например, воздействие оператора), удобно сформировать суммарную стандартную неопределенность u ( xi ) , которая учитывает такие воздействия, или ввести дополнительные переменные в f (х1, х2. х N ).
Из-за ориентации на входные величины этот подход иногда называют восходящим походом оценки неопределенности.
Физическая интерпретация u ( y ) не является однозначной, так как она может включать члены, полученные на основе экспертной оценки, и таким образом u ( y ) лучше всего рассматривать как функцию, характеризующую степень доверия. Однако можно получить более прямую физическую интерпретацию, определив разброс результатов вычисления u ( y ) , который был бы получен, если бы все входные переменные изменялись случайным образом в соответствии с принятым для них распределением.
А.2 Принцип совместных исследований
А.2.1 Основная модель
Планирование эксперимента при совместных исследованиях, их организация и статистическая обработка подробно описаны в ИСО 5725-1 — ИСО 5725-6. Самая простая модель, лежащая в основе статистической обработки данных совместных исследований, задается уравнением:
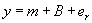
где m -математическое ожидание у;
В — лабораторная составляющая смещения в условиях повторяемости и предположения о нормальном распределении со средним 0 и стандартным отклонением σ L ;
е r — случайная ошибка в условиях повторяемости и предположения о нормальном распределении со средним 0 и стандартным отклонением σ w .
Кроме того, предполагается, что В и е r , некоррелированы.
Применение уравнения (А.1) к этой простой модели с учетом того, что σ w определяется через стандартное отклонение повторяемости sr , полученное при межлабораторном исследовании, приводит к уравнению (А.5) для единственного результата у и уравнению (А.6) для суммарной стандартной неопределенности результата u ( y ) :
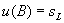
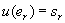
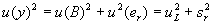
По сравнению с ИСО 5725-2 уравнение (А.6) представляет собой лишь оценку стандартного отклонения воспроизводимости sR .
Так как этот подход ориентируется на полное выполнение метода, его называют иногда нисходящим подходом.
Следует учитывать, что каждая лаборатория вычисляет свою оценку по уравнению у = f ( x 1 , х2. ), предполагая ее наилучшей оценкой измеряемой величины у для лаборатории. Тогда, если у = f ( x 1 , х2. ) — общая модель, используемая для описания поведения измерительной системы, то, следовательно, при вычислении m предполагается, что дисперсии, характеризующиеся оценками sL и sr , являются результатом изменения величин х1. хn. Если предполагается, что условия воспроизводимости обеспечиваются для случайной величины при всех существенных воздействиях и применяется физическая интерпретация u ( y ) , приведенная выше, то из этого следует, что u ( y ) в уравнении (А.6) является оценкой u ( y ) , описанной уравнениями (А.1) или (А.2).
Первый принцип, на котором основаны настоящие рекомендации, состоит в том, что стандартное отклонение воспроизводимости, полученное в совместном исследовании, является основой для оценки неопределенности измерений.
А.2.2 Включение данных правильности
Правильность в общем случае измеряется смещением относительно принятого опорного значения. В некоторых совместных исследованиях правильность метода в конкретной системе измерений (обычно СИ) исследуют путем анализа образца сравнения ( CRM ) или эталона единицы физической величины с сертифицированным значением 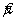
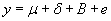
где μ — эталонное значение;
δ — смещение метода.
Совместное исследование может дать смещение 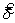
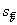
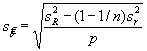
где n — количество повторений в каждой лаборатории;
р — количество лабораторий.
Неопределенность 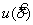
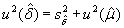
где 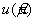
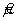
Если смещение, оцененное в процессе испытаний, используют при вычислении результатов в лабораториях, соответствующая ему неопределенность, если она не является незначительной, должна включаться в бюджет неопределенности.
А.2.3 Другие воздействия. Объединенная модель
На практике конечно sR и 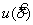
Проще всего учесть эти воздействия, рассматривая воздействие отклонений 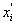
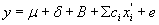
Суммирование ведется по всем воздействиям, кроме представленных в B , δ, е.
Примеры включают в себя воздействие отбора выборки, подготовки испытаний объекта и изменения состава или типа отдельных объектов испытаний. В строгом смысле это линеаризованная форма самой общей модели. При необходимости можно включать в нее члены более высокого порядка или члены, учитывающие корреляцию, как описано в [1] .
Очевидно, что центрирование 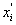
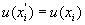
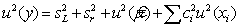
Суммирование ведется по воздействиям, не учтенным в других членах уравнения.
Следует отметить, что при оценке выполнения метода условия промежуточной прецизионности также могут быть описаны уравнением (А.10), хотя число членов суммы соответственно будет больше, поскольку по сравнению с условиями воспроизводимости в промежуточных условиях меньшее количество переменных будет меняться случайным образом. В общем случае уравнение (А.10) можно применять к любым условиям прецизионности, учитывая, что воздействия суммируются. В предельном случае, когда sr и sL равны нулю, а неопределенность общего смещения не определена, уравнение (А.11) становится идентичным уравнению (А.1).
Из этого следует два вывода:
— во-первых, необходимо продемонстрировать, что количественные данные, доступные для совместного исследования, согласуются с рассматриваемыми результатами испытаний;
— во-вторых, даже при согласованности данных совместного исследования для определения реальной оценки неопределенности с учетом дополнительных воздействий (х i в уравнении (А.10)) могут быть необходимы дополнительные исследования и предположения. При учете дополнительных воздействий предполагается применение уравнения (А.1).
И, наконец, настоящие рекомендации, утверждая, что надежную оценку неопределенности измерений можно получать на основе анализа данных воспроизводимости и правильности, полученных в соответствии с ИСО 5725-1 -ИСО 5725-6 , используют те же самые предположения, что и изложенные в перечисленных стандартах:
а) если используются данные воспроизводимости, предполагается, что все лаборатории подобны по выполнению работ. В частности, их прецизионность повторяемости для данного объекта испытаний одинакова, а лабораторная составляющая смещения В в уравнении (А.10) соответствует тому же распределению, что и при совместных исследованиях;
b ) испытываемые материалы, используемые в исследовании, являются гомогенными и стабильными.
Следующие разделы включают методологию проверки того, что дополнительные воздействия являются незначительными, а если это не так, их неопределенности учтены в оценке неопределенности результата.
А.3 Сопоставление подходов
Приведенные рассуждения описывают два очевидно различных подхода к оценке неопределенности. Подход GUM [1] описывает неопределенность в виде дисперсии, полученной на основе дисперсий соответствующих входных данных математической модели. Другой подход использует факт, что если одни и те же воздействия заметно изменяются в процессе исследования воспроизводимости, наблюдаемая дисперсия является оценкой той же самой неопределенности. На практике значения неопределенности, полученные на основе различных подходов, различны для разных целей, включая:
а) неполные математические модели (то есть при наличии неизвестных воздействий);
b ) неполное или несущественное изменение всех воздействующих факторов в процессе оценки воспроизводимости.
Сравнение двух различных оценок безусловно полезно для оценки полноты модели измерений. Однако следует обратить внимание, что наблюдаемую повторяемость или другую оценку прецизионности очень часто рассматривают как отдельную составляющую неопределенности даже в подходе GUM [1] . Точно так же индивидуальные воздействия обычно проверяют на их значимость или оценивают количественно до оценки воспроизводимости. На практике для оценки неопределенности часто используют некоторые элементы обоих подходов.
Когда оценка неопределенности для интерпретации сопровождается результатами, важно, чтобы пробелы в каждом подходе были заполнены. Возможности неполных моделей на практике обычно дополняют консервативными оценками, позволяющими расширять ограничения для неопределенности модели. В настоящих рекомендациях для устранения неадекватных изменений входных воздействий рекомендуется определять оценки дополнительных воздействий. Это является гибридным подходом, объединяя элементы и нисходящего, и восходящего подходов.
Приложение В (справочное)
Экспериментальная оценка неопределенности
B .1 Процедура оценки коэффициента чувствительности
Если входные величины xi могут изменяться непрерывно по всему диапазону значений, рекомендуется исследовать воздействие таких изменений. Простая процедура, предполагающая приблизительно линейную зависимость результатов от xi следующая:
а) выбирают подходящий диапазон изменения переменной xi , который должен быть ориентирован на лучшую оценку (или на значение, характерное для указанного метода);
b ) выполняют всю процедуру измерений (или ту часть, которая касается xi .) в каждом из пяти или более уровней xi с повторением при необходимости;
с) рассчитывают и изображают линейную модель в соответствии с результатами, используя xi в качестве абсциссы, а результат измерений в качестве ординаты;
d ) коэффициентом чувствительности является наклон прямой, характеризуемый коэффициентом ci , в уравнениях (А.1) или (А.2).
Этот подход может дать различные коэффициенты чувствительности для различных объектов испытаний. Это может быть преимуществом во всесторонних исследованиях конкретного объекта или класса объектов. Однако если коэффициент чувствительности должен быть применен к большому диапазону различных ситуаций, важно проверять, чтобы различные объекты вели себя аналогично.
B .2 Простая процедура оценки неопределенности, вызванной случайным воздействием
Если входные величины xj , являются дискретными и/или неконтролируемыми, соответствующую неопределенность можно получать на основе анализа экспериментов, в которых переменная изменяется случайным образом. Например, тип почвы в экологических исследованиях может иметь непредсказуемое воздействие на результаты анализа. Если случайные ошибки не зависят от уровня исследуемой величины, можно исследовать дисперсию ошибки, являющейся результатом таких изменений, используя серию объектов, для которых заданное значение или доступно, или, если изменение известно, может быть выведено теоретически.
Общая процедура включает в себя:
а) выполнение полного измерения на представительном наборе объектов испытаний в условиях повторяемости, используя равное количество повторений для каждого объекта;
b ) вычисление разности с заданным значением для каждого наблюдения;
с) проведение анализа результатов (ранжированных по величине) в соответствие с ANOVA с использованием суммы квадратов для формирования оценок внутригрупповой составляющей дисперсии 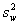
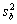
Примечание — Если различные объекты или классы объектов по-разному реагируют на исследуемую величину (то есть существует взаимосвязь величины и класса исследуемых объектов), взаимодействие увеличивает значение sb. Детальное исследование этой ситуации в настоящих рекомендациях не приводится.
Приложение С (справочное)
Примеры расчета неопределенности
С.1 Измерение содержания монооксида углерода (СО) в отработавших газах автомобиля
До выпуска на рынок легковые автомобили должны проходить испытания типа транспортного средства для проверки выполнения регулирующих требований относительно количества монооксида углерода в отработавших газах. Верхний предел составляет 2,2 г/км. Метод испытаний описан в Директиве ЕН 70/220 [4], где введены следующие требования:
— цикл двигателя задается как функция скорости (км/ч), времени (с) и оборотов двигателя. Исследуемый автомобиль помещают на специальные ролики для выполнения заданного количества циклов;
— измерительное оборудование — газоанализатор на СО;
— контроль окружающей среды проводят с использованием специальной камеры мониторинга загрязнений;
— персонал имеет специальную подготовку.
Такие испытания на соответствие можно выполнять в испытательной лаборатории предприятия по производству автомобилей или в независимой испытательной лаборатории.
С.1.2 Данные совместных исследований
Перед принятием и использованием такого метода испытаний необходимо оценивать факторы или источники, влияющие на результаты метода испытаний (и, следовательно, на неопределенность результатов испытаний). Такая оценка выполнялась по данным экспериментов, проводимых в различных лабораториях. Для контроля метода испытаний межлабораторный эксперимент проводился в соответствии с ИСО 5725-2. Цель межлабораторного эксперимента состоит в том, чтобы оценить прецизионность метода испытаний при применении его в данном наборе испытательных лабораторий. Оценка прецизионности получена на основе данных, собранных в межлабораторном эксперименте со статистическим анализом в соответствии с ИСО 5725-2. Исследование проводят так, чтобы каждый участник выполнял все необходимые процессы измерений и учитывая воздействующие факторы.
Было установлено, что повторяемость лабораторий значимо не различается, а оценка стандартного отклонения повторяемости метода испытаний равна 0,22 г/км. Оценка стандартного отклонения воспроизводимости метода испытаний равна 0,28 г/км.
С.1.3 Контроль смещения
Оценка правильности (контроль смещения по отношению к эталону) включает в себя методологические и технические вопросы. Не существует «эталонного автомобиля» как образца сравнения. Правильность следует контролировать при калибровке системы испытаний. Например, калибровку анализатора СО можно выполнять с помощью эталонного газа, а калибровку испытательного стенда можно выполнять для величин, таких как время, длина, скорость и ускорение. Знание норм выбросов для различных скоростей и наличие другой аналогичной информации подтверждают, что неопределенность, связанная с этими калибровками, не дает существенных вкладов в неопределенность, связанную с результатами измерений (то есть вся расчетная неопределенность много меньше, чем стандартное отклонение воспроизводимости). Смещение находится под контролем.
Типовые дублированные испытательные пробеги в лаборатории показали, что повторяемость приблизительно составляет 0,20 г/км и находится в пределах диапазона повторяемости, найденного при межлабораторном исследовании. Таким образом, прецизионность находится под хорошим контролем.
С.1.5 Соответствие объектов испытаний
Метод признают подходящим для всех транспортных средств, относящихся к легковым автомобилям. Хотя большинство транспортных средств признают соответствующими относительно легко и неопределенность имеет тенденцию уменьшаться для более низких уровней выхлопов, неопределенность важна на уровнях, близких к регулирующей границе. Поэтому было решено использовать оценку неопределенности, близкую к регулирующей границе, как корректную и несколько консервативную оценку неопределенности для более низких уровней выделения СО. Необходимо заметить, если испытания транспортного средства показывают выхлоп существенно больше установленной границы, может оказаться необходимым проведение дополнительных исследований неопределенности, если сравнения являются критичными. На практике, однако, такое транспортное средство в любом случае нельзя предлагать для продажи без его модернизации.
С.1.6 Оценка неопределенности
Поскольку предшествующие исследования установили должный контроль смещения и прецизионности в пределах испытательной лаборатории, а также отсутствие воздействующих факторов, не учтенных при совместных исследованиях, стандартное отклонение воспроизводимости, используемое для оценки стандартного отклонения неопределенности, дает расширенную неопределенность U = 0,56 г/км ( k = 2).
Примечание — Интерпретация неопределенности результатов в области проверки соответствия рассмотрена в ИСО 10576-1.
С.2 Определение состава мяса
Для продукции из мяса необходимо гарантировать, что состав мяса точно заявлен. Состав мяса определяют как комбинацию содержания азота (преобразованного к общему белку) и жира. Представленный пример показывает принцип объединения различных составляющих неопределенности, каждая из которых непосредственно следует в основном из оценок воспроизводимости, как описано в разделе 12.
С.2.2 Основные уравнения
Полный состав мяса Wmeat определяют в соответствии с уравнением:
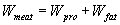
где Wpro — общий белок в мясе, выраженный в виде процента массы;
Wfat — общее содержание жира, выраженное в виде процента массы.
Белок в мясе Wpro вычисляют по формуле:
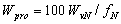
где fN является фактором азота, соответствующим материалу;
W vN — полное содержание азота в мясе.
В этом случае W mN идентично общему содержанию азота WtN , определяемому в соответствии с анализом Кьельдаля.
С.2.3 Экспериментальные шаги при определении состава мяса
При определении состава мяса применяют следующие экспериментальные шаги:
a ) определяют содержание жира Wfat ;
b ) определяют содержание азота W mN по Кьельдалю (среднее дублированных измерений);
с) вычисляют содержание обезжиренного мяса Wpro и fN (см. уравнение (С.2));
d ) вычисляют общий состав мяса Wmeat (см. уравнение (С.1)).
С.2.4 Составляющие неопределенности
Составляющие неопределенности связаны с каждой из величин, перечисленных в С.2.3. Наиболее существенным является Wpro составляющий приближенно 90 % массы Wmeat . Наибольшая неопределенность, связанная с Wpro , является результатом:
а) неопределенности фактора fN вследствие неполного знания материала;
b ) отклонений метода в условиях воспроизводимости при повторении метода и при точном выполнении метода в течение длительного времени;
с) неопределенности, связанной со смещением метода;
d ) неопределенности содержания жира Wfat .
Примечание — Неопределенности а), b) и с) связаны с образцом, лабораторией и методом соответственно. Часто бывает полезно грубо рассмотреть каждый из этих трех факторов при идентификации неопределенности, а также неопределенность отдельных шагов в процедуре.
С.2.5 Оценка составляющих неопределенности
С.2.5.1 Неопределенность, соответствующая fN
Неопределенность, соответствующая fN , может быть оценена по приведенному в публикациях диапазону значений. В [5] приведены результаты исследований содержания азота в говядине, которые показывают четкое отличие между различными источниками и кусками мяса. В [5] также даны рекомендации по вычислению наблюдаемого стандартного отклонения для fN = 0,052 и относительного стандартного отклонения 0,014 для большого диапазона типов выборок.
Примечание — Непосредственно применены данные содержания азота, определенные в [5], полученные с использованием метода Кьельдаля.
С.2.5.2 Неопределенность, соответствующая WtN
Информация о двух совместных испытаниях [6], [7] позволяет получать оценку неопределенности, вызванной плохой воспроизводимостью или ошибками выполнения метода. Тщательное расследование условий испытаний показывает, во-первых, что каждое исследование проводят по широкому диапазону типов выборки и с хорошим репрезентативным набором компетентных лабораторий, а во-вторых, что стандартное отклонение воспроизводимости sR хорошо коррелирует с уровнем азота. Для обоих испытаний наиболее подходящая линейная функция задается уравнением sR = 0,021 WtN. То же самое исследование показывает, что стандартное отклонение повторяемости пропорционально WtN = 0,018 WtN и межлабораторному члену sL = 0,011 WtN.
Метод таков, что каждое измерение дублируют и определяют выборочное среднее. Член, соответствующий повторяемости, который представляет собой оценку повторяемости единственного результата, должен быть соответствующим образом приспособлен для учета воздействия среднего двух результатов в лаборатории (см. комментарий, относящийся к sr в таблице 1). Неопределенность u ( WtN ) , соответствующая содержанию азота, имеет вид:
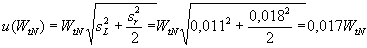
Уравнение (С.3) дает лучшую оценку неопределенности с WtN , соответствующей разумным изменениям при выполнении метода.
Воспроизводимость также используют в качестве критерия оценки прецизионности отдельной лаборатории. Метод устанавливает, что результаты должны быть отброшены, если данные попадают вне 95 %-ного доверительного интервала (приблизительно равного 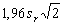
Примечание — Если эта проверка терпит неудачу чаще, чем в 5 % случаев, вероятно, что прецизионность не находится под достаточным контролем и необходимы действия по исправлению процедуры.
Необходимо также рассматривать неопределенность, соответствующую WtN и являющуюся результатом воздействия неизвестного смещения метода. В отсутствии надежных образцов сравнения сравнение с альтернативными методами, использующими другие принципы, является установленным средством оценки смещения. Сравнение метода Кьельдаля с методом анализа сжиганием для определения полного азота и различных типов выборки установило различие 0,01 WtN . Это удовлетворяет критерию 2 σD (см. ИСО Руководство 33, уравнение (4)), подтверждающему, что неопределенность, связанная со смещением, адекватна значениям воспроизводимости.
С.2.5.3 Неопределенность, соответствующая Wfat
Дополнительные данные совместных испытаний для анализа жира [8] дают оценку стандартного отклонения воспроизводимости 0,02 Wfat . Анализ снова выполняют дважды, а результаты принимают только в случае, если разность находится в соответствующих пределах повторяемости, гарантируя, что лабораторная прецизионность находится под контролем. Предшествующая верификация работы на подходящем образце сравнения для определения жира устанавливает, что неопределенность, связанная со смещением, адекватна значениям воспроизводимости.
С.2.6 Суммарная неопределенность
В таблице С.1 показаны индивидуальные значения и неопределенность, подсчитанная с использованием этих значений.
Таблица С.1 — Бюджет неопределенности для состава мяса