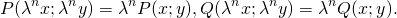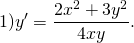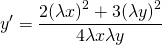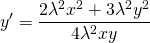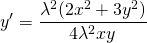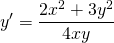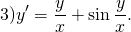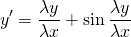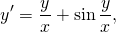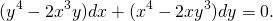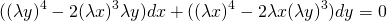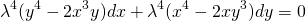Как отличить однородное дифференциальное уравнение от неоднородного

Видео:Однородное дифференциальное уравнениеСкачать

Как определить однородное уравнение

Дифференциальное уравнение 1-го порядка P(x;y)dx+Q(x;y)dy=0 называется однородным, если P(x;y) и Q(x;y) — однородные функции одинакового измерения, то есть

Как определить, что дифференциальное уравнение — однородное? На практике проверку уравнения на однородность проводят следующим образом: вместо каждого x подставляют λx, вместо каждого y — λy. При этом y’, dx и dy не трогают. После этого упрощают уравнение. Если после упрощения удается сократить на λ (или n- ю степень λ) и получить исходное уравнение, то это и означает, что данное уравнение является однородным уравнением 1-го порядка.

Другая форма записи: y’=f(x;y). Это уравнение является однородным, если функция f(x;y) является однородной функцией нулевого порядка. Это означает, что f(λx;λy)=f(x;y).

Подставляем вместо каждого x λx, вместо каждого y — λy:

Выносим лямбда в квадрате за скобки и сокращаем на него:

Пришли к исходному уравнению, а это значит, что данное уравнение — однородное.

2) (x-y)ydx-x²dy=0.

Подставляем вместо каждого x λx, вместо каждого y — λy: (λx-λy)λydx-(λx)²dy=0. Теперь выносим общий множитель λ² за скобки: λ²((x-y)ydx-x²dy)=0. Делим обе части уравнения на λ²:

(x-y)ydx-x²dy=0. Пришли к исходному уравнению, значит, это уравнение — однородное. (Здесь P(x;y) и Q(x;y) — однородные функции 2й степени).

Наличие дроби y/x уже косвенно указывает на то, что уравнение может быть однородным. Проверим, так ли это:

После сокращения на λ получаем исходное уравнение:

а это значит, что данное уравнение является однородным.

Подставляем вместо каждого x λx, вместо каждого y — λy:

Делим обе части уравнения на лямбда в 4й степени:

Получили исходное уравнение, а значит, оно является однородным. (Здесь P(x;y) и Q(x;y) — однородные функции 4й степени).

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения. Однородное уравнение.Скачать

Линейные дифференциальные уравнения высших порядков

Оговорим сразу тот факт, что нахождение решения общего аналитического вида для линейных однородных и неоднородных дифференциальных уравнений высших порядков зачастую невозможно. В основном пользуются приближенными методами решения.

Материал данной статьи представлен базовой теоретической информацией на тему решения ЛОДУ
n -ого порядка записи y ( n ) + f ( n — 1 ) ( x ) · y n — 1 + . . . + f 0 ( x ) · y = 0 и ЛНДУ n -ого порядка записи y ( n ) + f ( n — 1 ) ( x ) · y n — 1 + . . . + f 0 ( x ) · y = f ( x ) .

Сначала поговорим о линейных однородных дифференциальных уравнениях n -ого порядка, а затем займемся неоднородными ДУ.

Видео:4. Однородные дифференциальные уравнения (часть 1)Скачать

Линейные однородные дифференциальные уравнения

Общее решение для линейного однородного дифференциального уравнения n -ого порядка y ( n ) + f ( n — 1 ) ( x ) · y n — 1 + . . . + f 0 ( x ) · y = 0 при непрерывных на интервале интегрирования
X коэффициентах f 0 ( x ) , f 1 ( x ) , . . . , f n — 1 ( x ) определяет линейная комбинация y 0 = ∑ j = 1 n C j · y j , в которой y j , j = 1 , 2 , . . . , n являются линейно независимыми частными решениями ЛОДУ на X , а C j , j = 1 , 2 , . . . , n являются произвольными постоянными.

Когда тождество a 1 · y 1 + a 2 · y 2 + . . . + a n · y n ≡ 0 верно только при нулевых коэффициентах a 1 = a 2 = . . . = a n = 0 , функции y j , j = 1 , 2 , . . . , n являются линейно независимыми на неком интервале X .

Для линейно независимых функций y j , j = 1 , 2 , . . . , n определитель Вронского при любых
x из X отличен от нуля:

W ( x ) = y 1 y 2 … y n y ‘ 1 y ‘ 2 … y ‘ n y » 1 y » 2 … y » n … … … … y 1 ( n — 1 ) y 2 ( n — 1 ) … y n ( n — 1 ) ≠ 0

Тот факт, что определитель Вронского не равен нулю, возможно применять в качестве критерия линейной независимости функций на интервале.

Каким же образом определяются y j , j = 1 , 2 , . . . , n — линейно независимые частные решения линейного однородного дифференциального уравнения n -ого порядка?

В большинстве случаев данные функции возможно подобрать, используя стандартные системы линейно независимых функций:

1 ) 1 , x , x 2 , . . . , x n 2 ) e k 1 · x , e k 2 · x , . . . , e k n · x 3 ) e k 1 · x , x · e k 1 · x , . . . , x n 1 · e k 1 · x , e k 2 · x , x · e k 2 · x , . . . , x n 2 · e k 2 · x , . . . e k p · x , x · e k p · x , . . . , x n p · e k p · x

Когда подобраны все n линейно независимые частные решения y j , j = 1 , 2 , . . . , n , возможно составить общее решение линейного однородного дифференциального уравнения n -ого порядка y ( n ) + f ( n — 1 ) ( x ) · y n — 1 + . . . + f 0 ( x ) · y = 0 — оно будет иметь запись y 0 = ∑ j = 1 n C j · y j . Когда подобраны только несколько линейно независимых частных решений, мы можем понизить степень заданного уравнения при помощи замены. Детально этот пункт мы не будем рассматривать, в случае необходимости следует изучить дополнительные материалы по теме.

Видео:16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

Линейные неоднородные дифференциальные уравнения

Приступим к рассмотрению линейных неоднородных дифференциальных уравнений n -ого порядка записи y ( n ) + f ( n — 1 ) ( x ) · y n — 1 + . . . + f 0 ( x ) · y = f ( x ) .

Общее решение на интервале X линейного неоднородного дифференциального уравнения порядка n записи y ( n ) + f ( n — 1 ) ( x ) · y n — 1 + . . . + f 0 ( x ) · y = f ( x ) при непрерывных на интервале интегрирования X коэффициентах f 0 ( x ) , f 1 ( x ) , . . . , f n — 1 ( x ) и непрерывной функции f ( x ) определяется как сумма общего решения y 0 соответствующего ЛОДУ и некоторого частного решения y

заданного неоднородного уравнения: y = y 0 + y

Нахождение y 0 — общего решения соответствующего ЛОДУ n -ого порядка — было рассмотрено выше. Остается разобрать, как находится y

— частное решение линейного неоднородного дифференциального уравнения n -ого порядка.

Иногда некое частное решение y

бывает достаточно явным, то есть его возможно подобрать. Когда
y

подобрать затруднительно, при этом определены n линейно независимых частных решений y j , j = 1 , 2 , . . . , n соответствующего ЛОДУ, общее решение исходного ЛНДУ n -ого порядка возможно определить при помощи метода вариации произвольных постоянных.

В таком случае общее решение линейного неоднородного дифференциального уравнения y ( n ) + f ( n — 1 ) ( x ) · y n — 1 + . . . + f 0 ( x ) · y = f ( x ) определяется как y = ∑ j = 1 n C j ( x ) · y j , а функции C 1 ( x ) , C 2 ( x ) , … , C n ( x ) находятся интегрированием после решения системы уравнений:

∑ j = 1 n C j ‘ ( x ) · y j = 0 ∑ j = 1 n C j ‘ ( x ) · y ‘ j = 0 ∑ j = 1 n C j ‘ ( x ) · y » j = 0 … ∑ j = 1 n C j ‘ ( x ) · y j ( n — 2 ) = 0 ∑ j = 1 n C j ‘ ( x ) · y j ( n — 1 ) = 0

Видео:Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать

Линейные однородные дифференциальные уравнения и линейные неоднородные дифференциальные уравнения 2-го порядка

Линейные однородные дифференциальные уравнения (ЛОДУ) и линейные неоднородные дифференциальные уравнения (ЛНДУ) второго порядка .

Частным случаем дифференциальных уравнений (ДУ) такого типа называют линейные однородные дифференциальные уравнения и линейные неоднородные дифференциальные уравнения с постоянными коэффициентами.

Общее решение линейного однородного дифференциального уравнения на отрезке [a;b] представляет собой линейную комбинацию 2х линейно независимых частных решений y₁ и y₂ нашего уравнения, т.е.:

.

Самое сложное заключается в определении линейно независимых частных решений ДУ такого типа. Зачастую, частные решения выбирают из таких систем линейно независимых функций:

Но достаточно редко частные решения представляются именно так.

Примером линейного однородного дифференциального уравнения можно назвать .

Общее решение линейного неоднородного дифференциального уравнения определяется как ,

где y₀ является общим решением соответствующего линейного однородного дифференциального уравнения,

а является частным решением исходного ДУ. Метод определения y₀ мы сейчас обсудили, а вычисляют, используя метод вариации произвольных постоянных.

Как пример линейного неоднородного дифференциального уравнения приводим .

Познакомиться ближе с теорией и просмотреть примеры решений можете здесь: Линейные дифференциальные уравнения второго порядка.

💡 Видео

Дифференциальные уравнения, 3 урок, Однородные уравненияСкачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Однородные и неоднородные определения. Различить легко!Скачать

Математика без Ху!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.Скачать

6. Дифференциальные уравнения, приводящиеся к однороднымСкачать

13. Как решить дифференциальное уравнение первого порядка?Скачать

15. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентамиСкачать

18. Линейные неоднородные дифференциальные уравнения 2 порядка с постоянными коэффициентами. часть 3Скачать

Однородное линейное дифференциальное уравнение. Алгоритм решенияСкачать

Видеоурок "Нахождение частных решений по виду правой части"Скачать

Линейное неоднородное дифференциальное уравнение - bezbotvyСкачать

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

Линейные однородные дифференциальные уравнения n-го порядка с постоянными коэффициентамСкачать