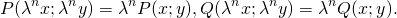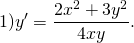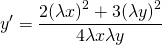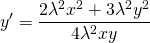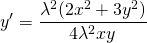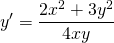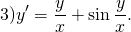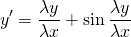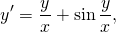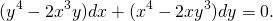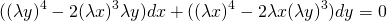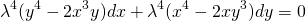Как отличить однородное дифференциальное уравнение от линейного

Думаю, нам стоит начать с истории такого славного математического инструмента как дифференциальные уравнения. Как и все дифференциальные и интегральные исчисления, эти уравнения были изобретены Ньютоном в конце 17-го века. Он считал именно это своё открытие настолько важным, что даже зашифровал послание, которое сегодня можно перевести примерно так: «Все законы природы описываются дифференциальными уравнениями». Это может показаться преувеличением, но всё так и есть. Любой закон физики, химии, биологии можно описать этими уравнениями.

Огромный вклад в развитие и создание теории дифференциальных уравнений внесли математики Эйлер и Лагранж. Уже в 18-м веке они открыли и развили то, что сейчас изучают на старших курсах университетов.

Новая веха в изучении дифференциальных уравнений началась благодаря Анри Пуанкаре. Он создал «качественную теорию дифференциальных уравнений», которая в сочетании с теорией функций комплексного переменного внесла значительный вклад в основание топологии — науки о пространстве и его свойствах.

Видео:Однородное дифференциальное уравнениеСкачать

Что такое дифференциальные уравнения?

Многие боятся одного словосочетания «дифференциальное уравнение». Однако в этой статье мы подробно изложим всю суть этого очень полезного математического аппарата, который на самом деле не так сложен, как кажется из названия. Для того чтобы начать рассказывать про дифференциальные уравнения первого порядка, следует сначала познакомиться с основными понятиями, которые неотъемлемо связаны с этим определением. И начнём мы с дифференциала.

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения. Однородное уравнение.Скачать

Дифференциал

Многие знают это понятие ещё со школы. Однако всё же остановимся на нём поподробнее. Представьте себе график функции. Мы можем увеличить его до такой степени, что любой его отрезок примет вид прямой линии. На ней возьмём две точки, находящиеся бесконечно близко друг к другу. Разность их координат (x или y) будет бесконечно малой величиной. Ее и называют дифференциалом и обозначают знаками dy (дифференциал от y) и dx (дифференциал от x). Очень важно понимать, что дифференциал не является конечной величиной, и в этом заключается его смысл и основная функция.

А теперь необходимо рассмотреть следующий элемент, который нам пригодится при объяснении понятия дифференциального уравнения. Это — производная.

Видео:4. Однородные дифференциальные уравнения (часть 1)Скачать

Производная

Все мы наверняка слышали в школе и это понятие. Говорят, что производная — это скорость роста или убывания функции. Однако из этого определения многое становится непонятным. Попробуем объяснить производную через дифференциалы. Давайте вернёмся к бесконечно малому отрезку функции с двумя точками, которые находятся на минимальном расстоянии друг от друга. Но даже за это расстояние функция успевает измениться на какую-то величину. И чтобы описать это изменение и придумали производную, которую иначе можно записать как отношение дифференциалов: f(x)’=df/dx.

Теперь стоит рассмотреть основные свойства производной. Их всего три:

1. Производную суммы или разности можно представить как сумму или разность производных: (a+b)’=a’+b’ и (a-b)’=a’-b’.
2. Второе свойство связано с умножением. Производная произведения — это сумма произведений одной функции на производную другой: (a*b)’=a’*b+a*b’.
3. Производную разности записать можно в виде следующего равенства: (a/b)’=(a’*b-a*b’)/b 2 .

Все эти свойства нам пригодятся для нахождения решений дифференциальных уравнений первого порядка.

Также бывают частные производные. Допустим, у нас есть функция z, которая зависит от переменных x и y. Чтобы вычислить частную производную этой функции, скажем, по x, нам необходимо принять переменную y за постоянную и просто продифференцировать.

Видео:Линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами.Скачать

Интеграл

Другое важное понятие — интеграл. По сути это прямая противоположность производной. Интегралы бывают нескольких видов, но для решения простейших дифференциальных уравнений нам понадобятся самые тривиальные неопределённые интегралы.

Итак, что такое интеграл? Допустим, у нас есть некоторая зависимость f от x. Мы возьмём от неё интеграл и получим функцию F(x) (часто её называют первообразной), производная от которой равна первоначальной функции. Таким образом F(x)’=f(x). Отсюда следует также, что интеграл от производной равен первоначальной функции.

При решении дифференциальных уравнений очень важно понимать смысл и функцию интеграла, так как придётся очень часто их брать для нахождения решения.

Уравнения бывают разными в зависимости от своей природы. В следующем разделе мы рассмотрим виды дифференциальных уравнений первого порядка, а потом и научимся их решать.

Видео:15. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентамиСкачать

Классы дифференциальных уравнений

«Диффуры» делятся по порядку производных, участвующих в них. Таким образом бывает первый, второй, третий и более порядок. Их также можно поделить на несколько классов: обыкновенные и в частных производных.

В этой статье мы рассмотрим обыкновенные дифференциальные уравнения первого порядка. Примеры и способы их решения мы также обсудим в следующих разделах. Будем рассматривать только ОДУ, потому что это самые распространённые виды уравнений. Обыкновенные делятся на подвиды: с разделяющимися переменными, однородные и неоднородные. Далее вы узнаете, чем они отличаются друг от друга, и научитесь их решать.

Кроме того, эти уравнения можно объединять, чтобы после у нас получилась система дифференциальных уравнений первого порядка. Такие системы мы тоже рассмотрим и научимся решать.

Почему мы рассматриваем только первый порядок? Потому что нужно начинать с простого, а описать всё, связанное с дифференциальными уравнениями, в одной статье просто невозможно.

Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Уравнения с разделяющимися переменными

Это, пожалуй, самые простые дифференциальные уравнения первого порядка. К ним относятся примеры, которые можно записать так: y’=f(x)*f(y). Для решения этого уравнения нам понадобится формула представления производной как отношения дифференциалов: y’=dy/dx. С помощью неё получаем такое уравнение: dy/dx=f(x)*f(y). Теперь мы можем обратиться к методу решения стандартных примеров: разделим переменные по частям, т. е. перенесём всё с переменной y в часть, где находится dy, и так же сделаем с переменной x. Получим уравнение вида: dy/f(y)=f(x)dx, которое решается взятием интегралов от обеих частей. Не стоит забывать и о константе, которую нужно ставить после взятия интеграла.

Решение любого «диффура» — это функция зависимости x от y (в нашем случае) или, если присутствует численное условие, то ответ в виде числа. Разберём на конкретном примере весь ход решения:

Переносим переменные в разные стороны:

Теперь берём интегралы. Все их можно найти в специальной таблице интегралов. И получаем:

Если требуется, мы можем выразить «игрек» как функцию от «икс». Теперь можно сказать, что наше дифференциальное уравнение решено, если не задано условие. Может быть задано условие, например, y(п/2)=e. Тогда мы просто подставляем значение этих переменных в решение и находим значение постоянной. В нашем примере оно равно 1.

Видео:Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать

Однородные дифференциальные уравнения первого порядка

Теперь переходим к более сложной части. Однородные дифференциальные уравнения первого порядка можно записать в общем виде так: y’=z(x,y). Следует заметить, что правая функция от двух переменных однородна, и её нельзя разделить на две зависимости: z от x и z от y. Проверить, является ли уравнение однородным или нет, достаточно просто: мы делаем замену x=k*x и y=k*y. Теперь сокращаем все k. Если все эти буквы сократились, значит уравнение однородное и можно смело приступать к его решению. Забегая вперёд, скажем: принцип решения этих примеров тоже очень прост.

Нам нужно сделать замену: y=t(x)*x, где t — некая функция, которая тоже зависит от x. Тогда мы можем выразить производную: y’=t'(x)*x+t. Подставляя всё это в наше исходное уравнение и упрощая его, мы получаем пример с разделяющимися переменными t и x. Решаем его и получаем зависимость t(x). Когда мы ее получили, то просто подставляем в нашу предыдущую замену y=t(x)*x. Тогда получаем зависимость y от x.

Чтобы было понятнее, разберём пример: x*y’=y-x*e y/x .

При проверке с заменой всё сокращается. Значит, уравнение действительно однородное. Теперь делаем другую замену, о которой мы говорили: y=t(x)*x и y’=t'(x)*x+t(x). После упрощения получаем следующее уравнение: t'(x)*x=-e t . Решаем получившийся пример с разделёнными переменными и получаем: e -t =ln(C*x). Нам осталось только заменить t на y/x (ведь если y=t*x, то t=y/x), и мы получаем ответ: e -y/x =ln(x*С).

Видео:Однородное линейное дифференциальное уравнение. Алгоритм решенияСкачать

Линейные дифференциальные уравнения первого порядка

Пришло время рассмотреть ещё одну обширную тему. Мы разберём неоднородные дифференциальные уравнения первого порядка. Чем они отличаются от предыдущих двух? Давайте разберёмся. Линейные дифференциальные уравнения первого порядка в общем виде можно записать таким равенством: y’ + g(x)*y=z(x). Стоит уточнить, что z(x) и g(x) могут являться постоянными величинами.

А теперь пример: y’ — y*x=x 2 .

Существует два способа решения, и мы по порядку разберём оба. Первый — метод вариации произвольных констант.

Для того чтобы решить уравнение этим способом, необходимо сначала приравнять правую часть к нулю и решить получившееся уравнение, которое после переноса частей примет вид:

Теперь надо заменить константу C₁ на функцию v(x), которую нам предстоит найти.

Проведём замену производной:

y’=v’*e x2/2 -x*v*e x2/2 .

И подставим эти выражения в исходное уравнение:

v’*e x2/2 — x*v*e x2/2 + x*v*e x2/2 = x 2 .

Можно видеть, что в левой части сокращаются два слагаемых. Если в каком-то примере этого не произошло, значит вы что-то сделали не так. Продолжим:

Теперь решаем обычное уравнение, в котором нужно разделить переменные:

dv = x 2 *e — x2/2 dx.

Чтобы извлечь интеграл, нам придётся применить здесь интегрирование по частям. Однако это не тема нашей статьи. Если вам интересно, вы можете самостоятельно научиться выполнять такие действия. Это не сложно, и при достаточном навыке и внимательности не отнимает много времени.

Обратимся ко второму способу решения неоднородных уравнений: методу Бернулли. Какой подход быстрее и проще — решать только вам.

Итак, при решении уравнения этим методом нам необходимо сделать замену: y=k*n. Здесь k и n — некоторые зависящие от x функции. Тогда производная будет выглядеть так: y’=k’*n+k*n’. Подставляем обе замены в уравнение:

Теперь надо приравнять к нулю то, что находится в скобках. Теперь, если объединить два получившихся уравнения, получается система дифференциальных уравнений первого порядка, которую нужно решить:

Первое равенство решаем, как обычное уравнение. Для этого нужно разделить переменные:

Берём интеграл и получаем: ln(n)=x 2 /2. Тогда, если выразить n:

Теперь подставляем получившееся равенство во второе уравнение системы:

И преобразовывая, получаем то же самое равенство, что и в первом методе:

Мы также не будем разбирать дальнейшие действия. Стоит сказать, что поначалу решение дифференциальных уравнений первого порядка вызывает существенные трудности. Однако при более глубоком погружении в тему это начинает получаться всё лучше и лучше.

Видео:13. Как решить дифференциальное уравнение первого порядка?Скачать

Где используются дифференциальные уравнения?

Очень активно дифференциальные уравнения применяются в физике, так как почти все основные законы записываются в дифференциальной форме, а те формулы, которые мы видим — решение этих уравнений. В химии они используются по той же причине: основные законы выводятся с их помощью. В биологии дифференциальные уравнения используются для моделирования поведения систем, например хищник — жертва. Они также могут использоваться для создания моделей размножения, скажем, колонии микроорганизмов.

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Как дифференциальные уравнения помогут в жизни?

Ответ на этот вопрос прост: никак. Если вы не учёный или инженер, то вряд ли они вам пригодятся. Однако для общего развития не помешает знать, что такое дифференциальное уравнение и как оно решается. И тогда вопрос сына или дочки «что такое дифференциальное уравнение?» не поставит вас в тупик. Ну а если вы учёный или инженер, то и сами понимаете важность этой темы в любой науке. Но самое главное, что теперь на вопрос «как решить дифференциальное уравнение первого порядка?» вы всегда сможете дать ответ. Согласитесь, всегда приятно, когда понимаешь то, в чём люди даже боятся разобраться.

Видео:Дифференциальные уравнения, 3 урок, Однородные уравненияСкачать

Основные проблемы при изучении

Основной проблемой в понимании этой темы является плохой навык интегрирования и дифференцирования функций. Если вы плохо берёте производные и интегралы, то, наверное, стоит ещё поучиться, освоить разные методы интегрирования и дифференцирования, и только потом приступать к изучению того материала, что был описан в статье.

Некоторые люди удивляются, когда узнают, что dx можно переносить, ведь ранее (в школе) утверждалось, что дробь dy/dx неделима. Тут нужно почитать литературу по производной и понять, что она является отношением бесконечно малых величин, которыми можно манипулировать при решении уравнений.

Многие не сразу осознают, что решение дифференциальных уравнений первого порядка — это зачастую функция или неберущийся интеграл, и это заблуждение доставляет им немало хлопот.

Видео:Линейные однородные дифференциальные уравнения n-го порядка с постоянными коэффициентамСкачать

Что ещё можно изучить для лучшего понимания?

Лучше всего начать дальнейшее погружение в мир дифференциального исчисления со специализированных учебников, например, по математическому анализу для студентов нематематических специальностей. Затем можно переходить и к более специализированной литературе.

Стоит сказать, что, кроме дифференциальных, есть ещё интегральные уравнения, так что вам всегда будет к чему стремиться и что изучать.

Видео:Математика без Ху!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.Скачать

Заключение

Надеемся, что после прочтения этой статьи у вас появилось представление о том, что такое дифференциальные уравнения и как их правильно решать.

В любом случае математика каким-либо образом пригодится нам в жизни. Она развивает логику и внимание, без которых каждый человек как без рук.

Видео:7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

Как определить однородное уравнение

Дифференциальное уравнение 1-го порядка P(x;y)dx+Q(x;y)dy=0 называется однородным, если P(x;y) и Q(x;y) — однородные функции одинакового измерения, то есть

Как определить, что дифференциальное уравнение — однородное? На практике проверку уравнения на однородность проводят следующим образом: вместо каждого x подставляют λx, вместо каждого y — λy. При этом y’, dx и dy не трогают. После этого упрощают уравнение. Если после упрощения удается сократить на λ (или n- ю степень λ) и получить исходное уравнение, то это и означает, что данное уравнение является однородным уравнением 1-го порядка.

Другая форма записи: y’=f(x;y). Это уравнение является однородным, если функция f(x;y) является однородной функцией нулевого порядка. Это означает, что f(λx;λy)=f(x;y).

Подставляем вместо каждого x λx, вместо каждого y — λy:

Выносим лямбда в квадрате за скобки и сокращаем на него:

Пришли к исходному уравнению, а это значит, что данное уравнение — однородное.

2) (x-y)ydx-x²dy=0.

Подставляем вместо каждого x λx, вместо каждого y — λy: (λx-λy)λydx-(λx)²dy=0. Теперь выносим общий множитель λ² за скобки: λ²((x-y)ydx-x²dy)=0. Делим обе части уравнения на λ²:

(x-y)ydx-x²dy=0. Пришли к исходному уравнению, значит, это уравнение — однородное. (Здесь P(x;y) и Q(x;y) — однородные функции 2й степени).

Наличие дроби y/x уже косвенно указывает на то, что уравнение может быть однородным. Проверим, так ли это:

После сокращения на λ получаем исходное уравнение:

а это значит, что данное уравнение является однородным.

Подставляем вместо каждого x λx, вместо каждого y — λy:

Делим обе части уравнения на лямбда в 4й степени:

Получили исходное уравнение, а значит, оно является однородным. (Здесь P(x;y) и Q(x;y) — однородные функции 4й степени).

Видео:16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

16. Однородные и линейные уравнения первого порядка

Прежде всего, рассмотрим простые и важные классы уравнений первого порядка, приводящихся к уравнениям с разделяющимися переменными.

I. Однородные уравнения.

Называется однородным, если функция может быть представлена как функция отношения своих аргументоВ:

Однородное, так как его можно записать в виде

В общем случае переменные в однородном уравнении не разделяются. Однако, вводя вспомогательную неизвестную функцию U по формуле

или

Мы сможем преобразовать однородное уравнение в уравнение с разделяющимися переменными.

И уравнение прИНимает вид

, т. е.

После интегрирования получаем:

Найдя отсюда выражение для И как функции от Х, и возвращаясь к переменной , получим искомое решение однородного уравнения.

Чаще всего не удается просто найти явное выражение для И. Тогда после интегрирования следует в левую часть вместо U ПодстаВить ; в результате мы получим решение уравнения в неявном виде.

Разумеется, мы предполагаем, что . Если , то и не нужно делать никаких преобразований, ибо само заданное уравнение — с разделяющимися переменными.

Нет необходимости запоминать полученные выше формулы: в каждом примере нетрудно проделать полностью указанное преобразование.

Пример. Найдем решение однородного уравнения

Замена приводит к уравнению

или

Разделяя переменные, находим:

, или

Возвращаясь к перемеННой У, приходим к общему решению:

II. Линейные уравнения. Вторым часто встречающимся типом уравнений первого порядка явлЯЕтся линейное уравнение.

Определение. Уравнение вида

(*)

Т. Е. линейное относительно искомой фуНКции и ее производНОй, называется линейным.

Здесь Р(Х) и Q(Х) — известные функции независимой переменной Х.

Уравнение (*) сводится к двум уравнениям с разделяющимися переменными путем следующего искусственного приема. Запишем функцию У в виде произведения двух функций: . одной из них мы можем распорядиться совершенно произвольно; при этом вторая должна быть определена в зависимости от первой таким образом, чтобы их произведение удовлетворяло данному линейному уравнению. Свободой выбора одной иЗ функций U и N мы воспользуемся для максимального упрощения уравнения, получающегося после замены.

Из равенства находим производную У’:

Подставляя это выражение в уравнение (*), имеем:

, или .

Выберем в качестве N какое-нибудь частное решение уравнения

. (**)

Тогда для отыскания U получим уравнение

. (***)

Сначала найдем N из уравнения (**). Разделяя переменные, имеем:

и .

Как и раньше, под неопределенным интегралом здесь понимается Какая-нибудь одна первообразная от функции Р(Х), т. е. N является вполне определенной функцией от Х.

Зная N, находим далее И из уравнения (***):

Здесь мы уже берем для U все первообразные. По И и N найдем искомую функцию У:

Полученная формула дает общее решение линейного уравнения (*).

Положение не изменится, если мы прибавим произвольную постоянную к интегралу в показателе. В самом деле, эта вторая произвольная постоянная в конечном счете исчезнет, так как один множитель будет содержать ее в знаменателе, а другой — в числителе.

Можно решать задачу с помощью определенных интегралов с переменным верхним пределом. При этом

Частное решение, соответствующее начальному условию , Получается отсюда при .

Как и раньше, мы не настаиваем на запоминании общей формулы. Следует помнить лишь способ решения и применять его в каждом конкретном случае.

Пример. Решим уравнение

Положим , тогда . Имеем: или Пусть . Отсюда и, значит, Т. е. Следовательно, откуда и, значит, Имеем окончательно:

.

Рассмотрим одну важную задачу электротехники, которая приведет нас к линейному дифференциальному уравнению первого порядка. Пусть ЭЛектрическая цепь имеет сопротивление R и самоиндукцию L.

Если через I обозначить силу тока в цепи, а через Е электродвижущую силу, то, как известно из физики,

.

Считая, что Е является известной функцией времени, получаем линейное уравнение, которое запишем в виде

Проинтегрируем это уравнение в предположении, что при начальном условии . Это означает, что мы включаем в цепь, в которой не было тока, постоянную электродвижущую силу. Воспользовавшись общей формулой, выраженной при помощи определенных интегралов, получим:

Или, выполняя интегрирование,

.

Ток I слагается как бы из двух токов: тока , соответствующего закону Ома, и экстратока замыкания , протекающего в обратном направлении. Экстраток замыкания быстро стремится к нулю, и поэтому в цепи довольно скоро устанавливается постоянный ток. Еще проще решается задача о размыкании цепи. В этом случае мы считаем, что и . Тогда получается уравнение с разделяющимися переменными Решая его, ПолуЧиМ — экстраток размыкания. Скорость СтремЛения экстратока к нулю зависит от отношения : чем это отношение больше, тем быстрее экстраток затухает.

Рекомендуем читателю самостоятельно решить задачу в случае, когда электродвижущая сила Е синусоидальна, т. е. когда .

📺 Видео

ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

Линейное дифференциальное уравнение Коши-ЭйлераСкачать

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Линейное дифференциальное уравнение первого порядка (1-x^2)*y'-xy=1Скачать