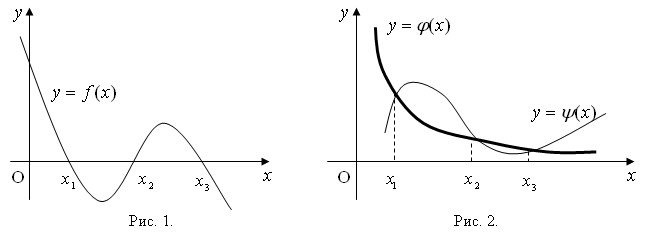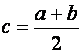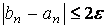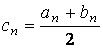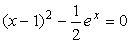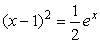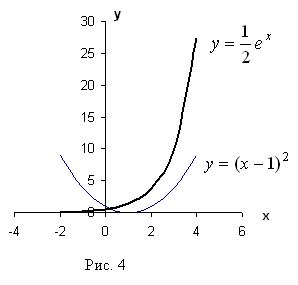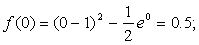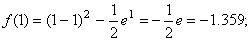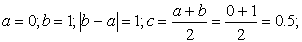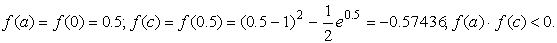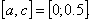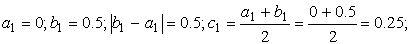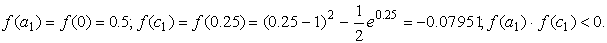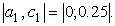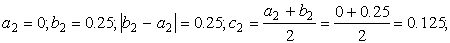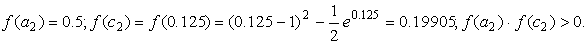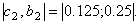Цель работы
Целью работы является изучение численных методов решения алгебраических и трансцендентных уравнений. В настоящей работе рассматриваются следующие методы нахождения корней уравнения :
· — Метод деления отрезка пополам.
· — Метод касательных (Метод Ньютона).
Примеры заданий
Найти корни уравнений :
1. x 2 — 0.5 + sin(x) =0;
2. 2 * sin(x) — x 2 + 0.3 * x = 0;
3. 0.1 * sin(x) + x 3 — 1 = 0;
4. 0.1 * x 2 — x * Ln(x) = 0;
5. 0.1 * x 3 — 2 * x 2 + x — 5 = 0;
6. x 3 — 0.39 * x 2 — 10.5 * x + 11 = 0;
8. 2.5 — 3 * sin(x + Pi / 4) = 0 ;
9. abs(x) + cos(x + Pi / 8) — 2.5 = 0.
Найти минимальный положительный корень :
10. sin(x) = P — q * x, 0 0;
13. Ln(x) = P — q * x 2 , P,q > 0.
Теоретические сведения
Пусть уравнение имеет вид f(x) = 0. Функция f(x) определена в некотором конечном или бесконечном интервале a
6.3.4 Метод деления отрезка пополам
Дана функция f(x) непрерывная на отрезке a,b и удовлетворяющая условию f(a) * f(b) k .
При k ® 


Процесс деления отрезка прекращается при условии, что
Противоположная граница будет неподвижной (точка d). Вычисления корня прекращаются при условии, что
Видео:Информатика 2. S01.E08. Отделение корня уравненияСкачать

Реферат на тему «Отделяем корни аналитически»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику
Лабораторная работа №2
Отделить корни аналитически:
F(x)=
F (0) F (2)>0 Корень находится на отрезке [0, 2]
Построим таблицу на отрезке [0, 5 ]
Из таблицы видно, что корень находится на отрезке [1, 2], т.к. F (1)=-1 F (2)=1,785>0.
Функция возрастает, т.к производная положительная
F ’( x )= 

Ответ: Корень находится на отрезке [1, 2].
2. Отделить корни аналитически и уточнить один из них методом проб:
Найдем промежутки возрастания и убывания функции.
F ’( x )=4 x 


При х 
На отрезке [- 



Видео:Отделение корней уравнений аналитическим методом. Уточнение корней методом половинного деленияСкачать

Как отделить корни уравнения аналитически
1. Приближенное решение нелинейных уравнений
Пусть дано уравнение с одним неизвестным
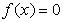
где f ( x ) — заданная алгебраическая или трансцендентная функция.
Функция называется алгебраической, если для получения её значения нужно выполнить арифметические операции и возведение в степень с рациональным показателем. Примеры трансцендентных функций — показательная , логарифмическая, тригонометрические, обратные тригонометрические.
Решить уравнение — значит найти все его корни, то есть те значения х , которые обращают уравнение в тождество, или доказать, что корней нет.
В общем случае не существует формул, по которым определяются точные значения корней уравнения (1.1). Для отыскания корней используют приближенные методы, при этом корни находятся с некоторой заданной точностью ε . Это означает, что если x — точное значение корня уравнения, а x ’ — его приближенное значение с точностью ε , то | x — x ’ | ≤ ε . Если корень найден с точностью ε , то принято писать x = x ± ε .
Будем предполагать, что уравнение (1.1) имеет лишь изолированные корни, то есть для каждого корня существует окрестность, не содержащая других корней этого уравнения.
Приближенное решение уравнения состоит из двух этапов:
1. Отделение корней, то есть нахождение интервалов из области определения функции f ( x ), в каждом из которых содержится только один корень уравнения (1).
2. Уточнение корней до заданной точности.
Отделение корней можно проводить графически и аналитически.
Для того , чтобы графически отделить корни уравнения (1.1), строят график функции y = f ( x ). Абсциссы точек его пересечения с осью Ox есть действительные корни уравнения (рис. 1). Практически бывает удобнее заменить уравнение (1.1) равносильным ему уравнением
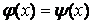
где Φ( x ) и Ψ( x ) — более простые функции, чем f ( x ). Абсциссы точек пересечения графиков функций y = Φ( x ) и y = Ψ( x ) дают корни уравнения (1.2), а значит и исходного уравнения (1.1) (рис.2).
Аналитическое отделение корней основано на следующей теореме: если непрерывная на отрезке [ a , b ] функция y = f ( x ) принимает на концах отрезка значения разных знаков, т.е. f ( a )· f ( b ) f ( x ) = 0; если при этом производная f ’ ( x ) сохраняет знак внутри отрезка [ a , b ], то корень является единственным.
Уточнение корней заключается в сужении интервала изоляции корня и выполняется одним из специальных методов. Рассмотрим самый простой из них — метод половинного деления.
Пусть корень отделён и принадлежит отрезку [ a , b ]. Находим середину отрезка [ a , b ] по формуле
Если f ( c ) = 0, то с — искомый корень. Если f ( c ) ≠ 0, то в качестве нового отрезка изоляции корня [ a 1 , b 1 ] выбираем ту половину [ a , c ] или [ c , b ], на концах которой f ( x ) принимает значения разных знаков. Другими словами, если f ( a ) ∙ f ( c ) a , c ], если f ( a ) ∙ f ( c ) — отрезку [ c , b ]. Полученный отрезок снова делим пополам, находим c1 ,
вычисляем f ( c 1 ), выбираем отрезок [ a 2 , b 2 ] и т.д. Длина каждого нового отрезка вдвое меньше длины предыдущего, то есть за n шагов отрезок сократится в 2 n раз. Как только будет выполнено условие
то в качестве приближенного значения корня, вычисленного с точностью ε , можно взять
Пример . Пусть требуется решить уравнение
с точностью ε = 0,0001. Отделим корень графически. Для этого преобразуем уравнение к виду
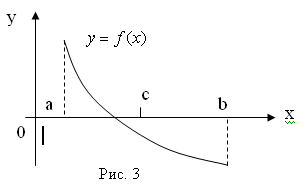
и построим графики функций (рис. 4):
Из рисунка видно, что абсцисса точки пересечения этих графиков принадлежит отрезку [0; 1].
Подтвердим аналитически правильность нахождения отрезка изоляции корня. Для отрезка [0; 1] имеем:
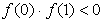
Уточнение корня выполним методом половинного деления.
Корень принадлежит отрезку
Корень принадлежит отрезку
Корень принадлежит отрезку
📸 Видео
Метод Ньютона (метод касательных) Пример РешенияСкачать

Как найти корни уравнения в Excel с помощью Подбора параметраСкачать

14 Метод половинного деления Ручной счет Численные методы решения нелинейного уравненияСкачать

Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать

7 класс, 35 урок, Графическое решение уравненийСкачать

Метод половинного деления решение нелинейного уравненияСкачать

Отбор корней по окружностиСкачать

Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

Метод половинного деления. ДихотомияСкачать

Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Метод Ньютона - отделение корнейСкачать

АЛГЕБРА 7 класс : Уравнение и его корни | ВидеоурокСкачать

Метод хордСкачать

Числовое решение. Функция root в MathCAD 14 (28/34)Скачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Консультация по решению задач по аналитической геометрии 2019-2020Скачать

5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать