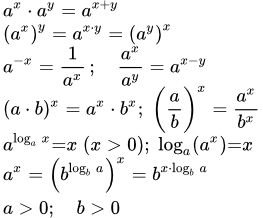Как определить уравнение показательной функции по графику

Видео:11 класс, 11 урок, Показательная функция, её свойства и графикСкачать

Показательная функция, ее свойства. Простейшие показательные уравнения

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На данном уроке мы рассмотрим показательную функцию, ее график и основные свойства. Также научимся решать простейшие показательные уравнения.

Если у вас возникнет сложность в понимании тему, рекомендуем посмотреть урок «Показательная функция и логарифм»

Видео:Показательная функция | 10 класс АлимовСкачать

Показательная функция – свойства, графики, формулы

Видео:Показательная функция. 11 класс.Скачать

Определение

Обобщение выполняется следующим образом.
При натуральном x = 1, 2, 3. , показательная функция является произведением x множителей:
.
При этом она обладает свойствами (1.5-8) (см. ниже ⇓), которые следуют из правил умножения чисел. При нулевом и отрицательных значениях целых чисел , показательную функцию определяют по формулам (1.9-10). При дробных значениях x = m/n рациональных чисел, , ее определяют по формуле(1.11). Для действительных , показательную функцию определяют как предел последовательности:
,
где – произвольная последовательность рациональных чисел, сходящаяся к x : .
При таком определении, показательная функция определена для всех , и удовлетворяет свойствам (1.5-8), как и для натуральных x .

Строгая математическая формулировка определения показательной функции и доказательство ее свойств приводится на странице «Определение и доказательство свойств показательной функции».

Видео:Алгебра 10 класс (Урок№21 - Показательная функция.)Скачать

Свойства показательной функции

Показательная функция y = a x , имеет следующие свойства на множестве действительных чисел ( ) :
(1.1) определена и непрерывна, при , для всех ;
(1.2) при a ≠ 1 имеет множество значений ;
(1.3) строго возрастает при , строго убывает при ,
является постоянной при ;
(1.4) при ;
при ;
(1.5) ;
(1.6) ;
(1.7) ;
(1.8) ;
(1.9) ;
(1.10) ;
(1.11) , .

Другие полезные формулы.
.
Формула преобразования к показательной функции с другим основанием степени:

При b = e , получаем выражение показательной функции через экспоненту:

Частные значения

Видео:ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать

Графики показательной функции

На рисунке представлены графики показательной функции
y ( x ) = a x
для четырех значений основания степени: a = 2 , a = 8 , a = 1/2 и a = 1/8 . Видно, что при a > 1 показательная функция монотонно возрастает. Чем больше основание степени a , тем более сильный рост. При 0 1 показательная функция монотонно убывает. Чем меньше показатель степени a , тем сильнее убывание.

Видео:Показательные уравнения. 11 класс.Скачать

Возрастание, убывание

Показательная функция, при является строго монотонной, поэтому экстремумов не имеет. Основные ее свойства представлены в таблице.

Видео:Показательная функцияСкачать

Обратная функция

Обратной для показательной функции с основанием степени a является логарифм по основанию a .

Если 0, ; a ne 1)» style=»width:203px;height:20px;vertical-align:-11px;background-position:-0px -492px»> , то
.
Если 0, ; a > 0, a ne 1)» style=»width:286px;height:20px;vertical-align:-11px;background-position:-386px -469px»> , то
.

Видео:ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ. ПОСТРОЕНИЕ ГРАФИКОВСкачать

Дифференцирование показательной функции

Для дифференцирования показательной функции, ее основание нужно привести к числу e , применить таблицу производных и правило дифференцирования сложной функции.

Для этого нужно использовать свойство логарифмов
и формулу из таблицы производных:
.

Пусть задана показательная функция:
.
Приводим ее к основанию e :

Применим правило дифференцирования сложной функции. Для этого вводим переменную

Тогда

Из таблице производных имеем (заменим переменную x на z ):
.
Поскольку – это постоянная, то производная z по x равна
.
По правилу дифференцирования сложной функции:
.

Производная показательной функции

Пример дифференцирования показательной функции

Найти производную функции
y = 3 5 x

Выразим основание показательной функции через число e .
3 = e ln 3
Тогда
.
Вводим переменную
.
Тогда

Из таблицы производных находим:
.
Поскольку 5ln 3 – это постоянная, то производная z по x равна:
.
По правилу дифференцирования сложной функции имеем:
.

Видео:Все графики функций за 20 секундСкачать

Интеграл

Видео:ЕГЭ/ Показательные и логарифмические графики функцийСкачать

Выражения через комплексные числа

Рассмотрим функцию комплексного числа z:
f ( z ) = a z
где z = x + iy ; i 2 = – 1 .
Выразим комплексную постоянную a через модуль r и аргумент φ :
a = r e i φ
Тогда

.
Аргумент φ определен не однозначно. В общем виде
φ = φ ₀ + 2 πn ,
где n – целое. Поэтому функция f ( z ) также не однозначна. Часто рассматривают ее главное значение
.

Видео:ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ график показательной функцииСкачать

Разложение в ряд

Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.

Автор: Олег Одинцов . Опубликовано: 21-02-2014 Изменено: 19-11-2018

Видео:Показательная функция. Видеоурок 10. Алгебра 10 классСкачать

Показательная функция: определение, формула, свойства, график

В данной публикации мы рассмотрим определение и формулу показательной функции, перечислим ее основные свойства, а также продемонстрируем, как выглядит ее график и приведем пример его построения.

Видео:ШМ. Задание 9. Показательная функция. Графики. Профильный ЕГЭ по математике 2022.Скачать

Определение показательной функции

Показательная функция – это функция вида , где:

• a – основание степени, при этом и ;
• x – показатель степени.

Примеры:

Видео:Логарифмическая функция, ее свойства и график. 11 класс.Скачать

Свойства показательной функции

1. Область определения – все действительные числа: .

Видео:Показательная функция, ее свойства и график | Алгебра 11 класс #7 | ИнфоурокСкачать

График показательной функции

Согласно Свойству 3, представленному выше, график показательной функции может быть:

• возрастающим при
• убывающим при

Асимптота – ось Ox , т.е. линия графика будет стремиться к оси абсцисс, но никогда не коснется ее.

Пример: построим график функции .

Для начала составим таблицу соответствия значений x и y .

💡 Видео

11 класс, 15 урок, Логарифмическая функция, её свойства и графикСкачать

Урок 1. Показательная функция. Свойства и график показательной функции. Алгебра 10, 11 класс.Скачать

✓ Логарифм. Начало | Показательная функция | Осторожно, спойлер! | Борис ТрушинСкачать

СТЕПЕННАЯ ФУНКЦИЯ график степенной функцииСкачать

Как запомнить графики функцийСкачать