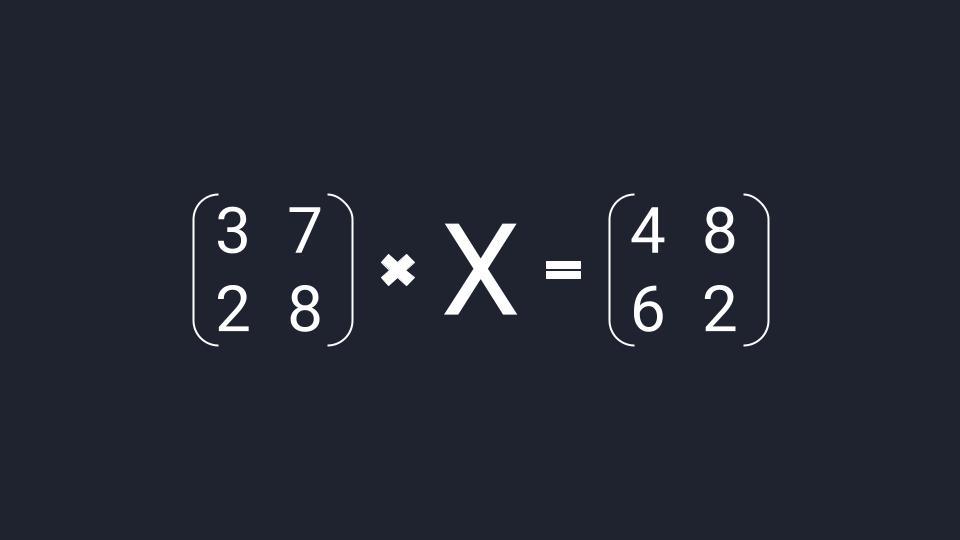Финальная глава саги.
Линейная алгебра и, в частности, матрицы — это основа математики нейросетей. Когда говорят «машинное обучение», на самом деле говорят «перемножение матриц», «решение матричных уравнений» и «поиск коэффициентов в матричных уравнениях».
Понятно, что между простой матрицей в линейной алгебре и нейросетью, которая генерирует котов, много слоёв усложнений, дополнительной логики, обучения и т. д. Но здесь мы говорим именно о фундаменте. Цель — чтобы стало понятно, из чего оно сделано.
Краткое содержание прошлых частей:
- Линейная алгебра изучает векторы, матрицы и другие понятия, которые относятся к упорядоченным наборам данных. Линейной алгебре интересно, как можно трансформировать эти упорядоченные данные, складывать и умножать, всячески обсчитывать и находить в них закономерности.
- Вектор — это набор упорядоченных данных в одном измерении. Можно упрощённо сказать, что это последовательность чисел.
- Матрица — это тоже набор упорядоченных данных, только уже не в одном измерении, а в двух (или даже больше).
- Матрицу можно представить как упорядоченную сумку с данными. И с этой сумкой как с единым целым можно совершать какие-то действия. Например, делить, умножать, менять знаки.
- Матрицы можно складывать и умножать на другие матрицы. Это как взять две сумки с данными и получить третью сумку, тоже с данными, только теперь какими-то новыми.
- Матрицы перемножаются по довольно замороченному алгоритму. Арифметика простая, а порядок перемножения довольно запутанный.
И вот наконец мы здесь: если мы можем перемножать матрицы, то мы можем и решить матричное уравнение.
❌ Никакого практического применения следующего материала в народном хозяйстве вы не увидите. Это чистая алгебра в несколько упрощённом виде. Отсюда до практики далёкий путь, поэтому, если нужно что-то практическое, — посмотрите, как мы генерим Чехова на цепях Маркова.
- Что такое матричное уравнение
- Шаг 1. Упрощаем уравнение
- Шаг 2. Вводим единичную матрицу
- Шаг 3. Находим обратную матрицу
- Шаг 4. Вычисляем неизвестную матрицу
- Шаг 5. Проверяем уравнение
- Ну и что
- Пример как работать с формулой массива в таблице Excel
- Примеры формул массива и отличие от обычных формул в Excel
- Когда формула является формулой массива, а когда обычной?
- Примеры как использовать формулу массива в Excel
- Как отличать формулу массива от обычной формулы
- Примеры вычислений и анализа формул массива
- Матричные уравнения
- 💥 Видео
Видео:C++ | Сложение элементов массиваСкачать

Что такое матричное уравнение
Матричное уравнение — это когда мы умножаем известную матрицу на матрицу Х и получаем новую матрицу. Наша задача — найти неизвестную матрицу Х.
Видео:Язык C++ с нуля | #33 Найти максимальный и минимальный элемент массива в c++Скачать

Шаг 1. Упрощаем уравнение
Вместо известных числовых матриц вводим в уравнение буквы: первую матрицу обозначаем буквой A, вторую — буквой B. Неизвестную матрицу X оставляем. Это упрощение поможет составить формулу и выразить X через известную матрицу.
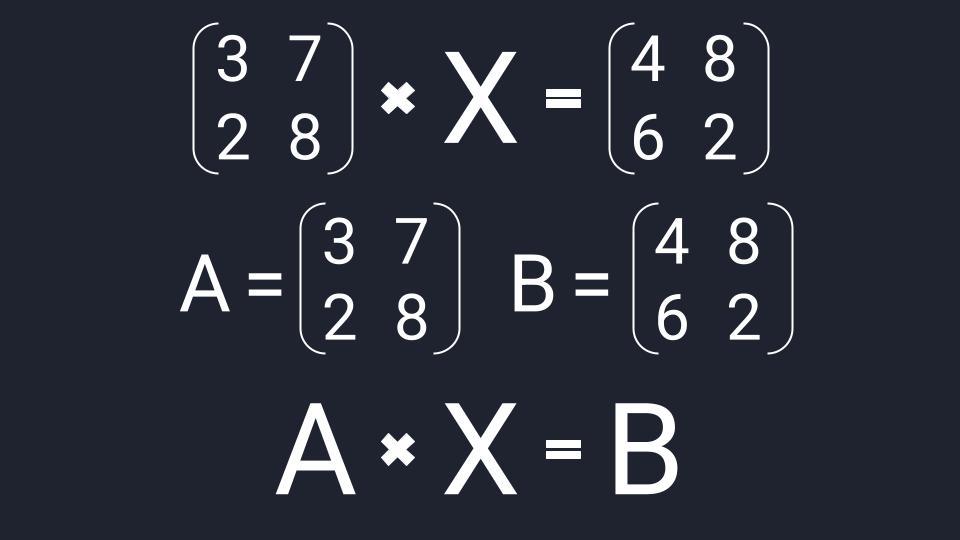
Видео:Найти минимальный элемент массива. Поиск минимального элемента в массиве. C++ для начинающих. ДЗ#8.Скачать

Шаг 2. Вводим единичную матрицу
В линейной алгебре есть два вспомогательных понятия: обратная матрица и единичная матрица. Единичная матрица состоит из нулей, а по диагонали у неё единицы. Обратная матрица — это такая, которая при умножении на исходную даёт единичную матрицу.
Можно представить, что есть число 100 — это «сто в первой степени», 100 1
И есть число 0,01 — это «сто в минус первой степени», 100 -1
При перемножении этих двух чисел получится единица:
100 1 × 100 -1 = 100 × 0,01 = 1.
Вот такое, только в мире матриц.
Зная свойства единичных и обратных матриц, делаем алгебраическое колдунство. Умножаем обе известные матрицы на обратную матрицу А -1 . Неизвестную матрицу Х оставляем без изменений и переписываем уравнение:
А -1 × А × Х = А -1 × В
Добавляем единичную матрицу и упрощаем запись:
А -1 × А = E — единичная матрица
E × Х = А -1 × В — единичная матрица, умноженная на исходную матрицу, даёт исходную матрицу. Единичную матрицу убираем
Х = А -1 × В — новая запись уравнения
После введения единичной матрицы мы нашли способ выражения неизвестной матрицы X через известные матрицы A и B.
💡 Смотрите, что произошло: раньше нам нужно было найти неизвестную матрицу. А теперь мы точно знаем, как её найти: нужно рассчитать обратную матрицу A -1 и умножить её на известную матрицу B. И то и другое — замороченные процедуры, но с точки зрения арифметики — просто.
Видео:Как найти количество уникальных элементов в массивеСкачать

Шаг 3. Находим обратную матрицу
Вспоминаем формулу и порядок расчёта обратной матрицы:
- Делим единицу на определитель матрицы A.
- Считаем транспонированную матрицу алгебраических дополнений.
- Перемножаем значения и получаем нужную матрицу.
Собираем формулу и получаем обратную матрицу. Для удобства умышленно оставляем перед матрицей дробное число, чтобы было проще считать.

Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Шаг 4. Вычисляем неизвестную матрицу
Нам остаётся посчитать матрицу X: умножаем обратную матрицу А -1 на матрицу B. Дробь держим за скобками и вносим в матрицу только при условии, что элементы новой матрицы будут кратны десяти — их можно умножить на дробь и получить целое число. Если кратных элементов не будет — дробь оставим за скобками.

Видео:Формулы массивов в Excel. Примеры использованияСкачать

Шаг 5. Проверяем уравнение
Мы решили матричное уравнение и получили красивый ответ с целыми числами. Выглядит правильно, но в случае с матрицами этого недостаточно. Чтобы проверить ответ, нам нужно вернуться к условию и умножить исходную матрицу A на матрицу X. В результате должна появиться матрица B. Если расчёты совпадут — мы всё сделали правильно. Если будут отличия — придётся решать заново.
👉 Часто начинающие математики пренебрегают финальной проверкой и считают её лишней тратой времени. Сегодня мы разобрали простое уравнение с двумя квадратными матрицами с четырьмя элементами в каждой. Когда элементов будет больше, в них легко запутаться и допустить ошибку.

Видео:Вывод массива. Массивы и циклы. Цикл с массивом. Array c++. C++ для начинающих. Урок #27.Скачать

Ну и что
Алгоритм решения матричных уравнений несложный, если знать отдельные его компоненты. Дальше на основе этих компонентов математики переходят в более сложные пространства: работают с многомерными матрицами, решают более сложные уравнения, постепенно выходят на всё более и более абстрактные уровни. И дальше, в конце пути, появляется датасет из миллионов котиков. Этот датасет раскладывается на пиксели, каждый пиксель оцифровывается, цифры подставляются в матрицы, и уже огромный алгоритм в автоматическом режиме генерирует изображение нейрокотика:
Видео:Решение задач на массивы в языке c++ | Практика на c++ урок 1.Скачать

Пример как работать с формулой массива в таблице Excel
Как узнать, является ли данная формула формулой массива? Что вообще она означает?
На этапе создания формула (или также функция) сама по себе не является ни формулой массива, ни обычной формулой. Это вы определяете, как Excel должен истолковать формулу, которую вы вводите. То, что формула является формулой массива – это не столько особенность самой формулы, а скорее способом, которым программа Excel введенную формулу «обрабатывает». Подтверждение формулы с помощью сочетания клавиш «Ctrl + Shitf + Enter» – это является для Excelя командой на выполнение (обработку данных) как массив вычислений. Тогда он используется в качестве аргумента функции и возвращает в качестве результата вычислений таблицу (массив данных).
Видео:КАК ПЕРЕВЕРНУТЬ МАССИВ !? СУММА ЧЕТНЫХ ЧИСЕЛ МАССИВА !? САМОЕ БОЛЬШОЕ ЧИСЛО В МАССИВЕ !? МАССИВЫ C#😱Скачать

Примеры формул массива и отличие от обычных формул в Excel
Некоторые функции Excelя по умолчанию в качестве аргумента принимают диапазон ячеек (массив) и в результате возвращают одно значение. Отличными примерами являются функции СУММ, СЧЕТЕСЛИ, СРЗНАЧ и т.д. Для этих функций не имеет никакого значения, вводите ли вы их как функции массива или нет. Они и так обрабатывают таблицы, и найдут выход (сработают правильно) из любой ситуации. Вот такие маленькие Excel-евские приспособленцы.
К счастью, существуют другие функции, которые работают совершенно иначе, т.е. в зависимости от вашего решения относительно их принадлежности к «функциям массива» (иногда они вообще не хотят работать). Прекрасным примером является функция ЕСЛИ.
Видео:Уравнения стороны треугольника и медианыСкачать

Когда формула является формулой массива, а когда обычной?
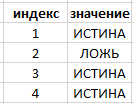
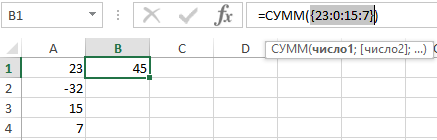
Для начала определимся как выглядит обычный массив значений в Excel. Это значения, которые находятся внутри фигурных скобок и разделены между собой точкой с запятой. Например:
– это синтаксис массива значений в Excel. Он может быть использован в аргументах функций.
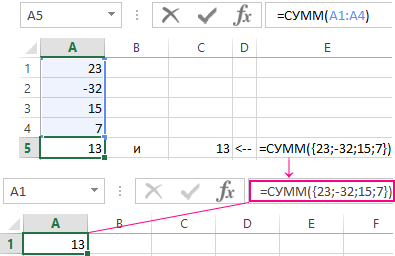
Диапазон ячеек A1:A4 – так же является массивом значений в Excel. Естественно так же используется в аргументах функций. Например сравним результаты вычислений двух формул: =СУММ(A1:A4) и =СУММ() – они идентичны:
Визуально формула массива находится так же внутри фигурных скобок, но они не должны быть введены вручную, а только лишь при помощи комбинации клавиш CTRL+SHIFT+Enter. Если ввести вручную фигурные скобки, то формула не будет выполнятся в массиве – это будет синтаксическая ошибка в Excel.
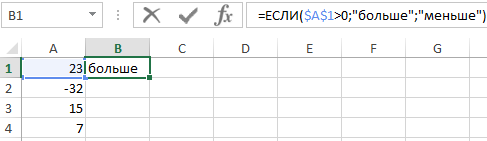
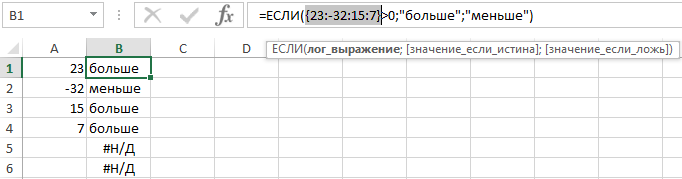
Формула массива (введенная с помощью сочитания CTRL+SHIFT+Enter) будет использоваться везде, где вы хотите, чтобы функция, которая обычно работает с отдельными значениями (ячейками), внезапно повела себя иначе и приняла в качестве аргумента и вернула в качестве результата массив значений (таблицу). Вернемся к уже упомянутой функции ЕСЛИ. В качестве аргумента она принимает логическое значение ИСТИНА или ЛОЖЬ. В классической форме:
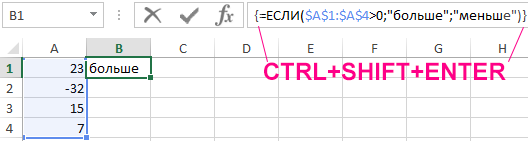
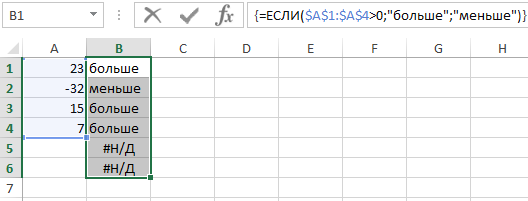
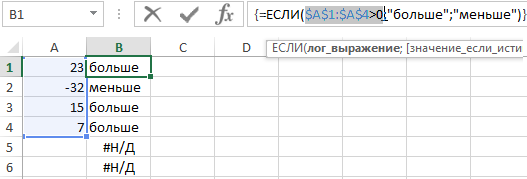
Если значение в ячейке A1 больше нуля, в качестве аргумента функция получит значение ИСТИНА и в качестве результата вернет текстовую строку «больше». Однако, если бы вы хотели проверить несколько ячеек сразу и передать результат такой проверки другой функции, вы должны были бы использовать вышеуказанную формулу как формулу массива. Для этого при вводе нажмем сочитание клавиш CTRL+SHIFT+Enter, а не как обычно (просто Enter):
В качестве аргумента функция принимает целый диапазон $A$1:$A$4. В результате проверки каждой ячейки диапазона в памяти компьютера создается таблица значений в массиве. Схематически таблицу можно отобразить так:
А так выглядят эти значения в массиве:
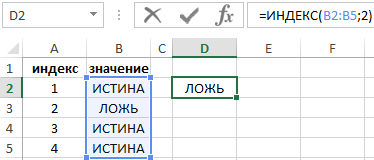
Например, чтобы прочитать этот массив и получить второе значение (сделать выборку значений) воспользуемся функцией:
Тоже самое что и:
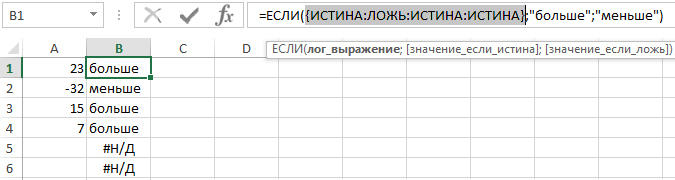
Затем создается другая таблица, значения которой зависят непосредственно от значений в первой таблице. Если элемент в первом массиве имеет значение ИСТИНА, во втором массиве он примет значение «больше». Если он имеет значение ЛОЖЬ, элемент во второй таблице примет значение «меньше». После этой операции первая таблица удаляется из памяти компьютера, и в конечном счете, функция возвращает массив . Схематически вторую таблицу можно отобразить так:
Так же ее можно прочитать функцией:
В примере с функцией ЕСЛИ была введена формула массива только в одну ячейку, поэтому в результате получили только одно значение, соответствующее первому значению в таблице. Однако достаточно ввести формулу массива в диапазон ячеек, чтобы увидеть все значения массива результатов. Для этого выделяем диапазон из нескольких ячеек, нажимаем клавишу F2 (или заново вводим формулу вручную) и жмем CTRL+SHIFT+Enter.
В примере (рисунок ниже) видно, что таблица результатов содержит ровно четыре элемента, о которых я упоминал выше.
Видео:Что такое массив. Примеры. Теория. Array. Одномерный массив. Синтаксис. C++. Урок #25.Скачать

Примеры как использовать формулу массива в Excel
Это все хорошо, но возникают некоторые вопросы: «Зачем же нужна формула массива?» или «Как или где использовать формулу в массиве?», «Чем она лучше обычной формулы?».
Разумеется, массив, возвращаемый функцией ЕСЛИ, может передаваться далее на «обработку» в качестве аргумента для другой функции.
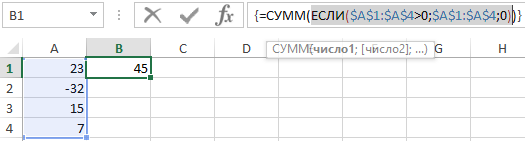
Пример. Представим, что вы хотели бы найти сумму ячеек B7:B10, но только тех, которые имеют значение больше нуля. Конечно же, вы можете использовать функцию СУММЕСЛИ, однако в нашем примере мы хотим сделать это только с помощью формулы массива. Суммируя значения ячеек нашего диапазона, необходимо будет как-то избавиться от значения «-32». Функции СУММ необходимо передать массив, в котором содержатся только значения больше нуля. Везде там, где значение меньше нуля, мы заменяем его на ноль, что, конечно же, не повлияет на результат. Как вы уже знаете, временную таблицу с соответствующими значениями вы можете получить, используя функцию ЕСЛИ. В конечном итоге соответствующая формула будет выглядеть так:
0;$A$1:$A$4;0))’ >
Вводим формулу и не забываем для подтверждения ввода нажать комбинацию клавиш CTRL+SHIFT+Enter. В результате проверки каждой ячейки диапазона $A$1:$A$4 (является ли значение больше нуля) в памяти компьютера создается массив . Затем создается очередная таблица. Если элемент в первом массиве имеет значение ИСТИНА, то во второй таблице будет отображаться значение из соответствующей ячейки. Если он имеет значение ЛОЖЬ, то элемент во второй таблице примет значение 0. После этой операции первая таблица удаляется из памяти компьютера, и в конечном итоге функция ЕСЛИ возвращает массив . Затем эта таблица передается в качестве аргумента функции =СУММ(), которая, согласно своему предназначению, возвращает сумму всех элементов в таблице. В нашем примере сумма равна 45. В завершении, посмотрите, что произойдет, если вы скажете Excelю обработать приведенную выше формулу не как формулу массива.
Ни одна из описанных выше таблиц, в этом случае, не будет создана. Только одна ячейка диапазона будет проверена (ячейка в той же строке, в которой находится функция). В нашем случае 15>0 значит, как первый аргумент функция ЕСЛИ получит логическое значение ИСТИНА. Затем ВЕСЬ диапазон A1:A4 будет передан функции СУММ, и в результате функция возвращает значение равное 13 (23-32+15+7). Если бы в ячейке вместо значения 15 было число меньше нуля, функция ЕСЛИ в качестве аргумента получила бы значение ЛОЖЬ, и, следовательно, только значение нуля было бы передано функции СУММ. Наша функция СУММ в результате также вернет значение равное нулю.
Видео:УРОК 9 -10. Максимальный и минимальный элемент массива (10 класс)Скачать

Как отличать формулу массива от обычной формулы
При нажатии клавиш CTRL+SHIFT+Enter для подтверждения ввода в строке формул будут отображены фигурные скобки по краям. Значит данная формула выполняется в массиве. Но что если еще на этапе создания неизвестно какой тип формул следует применять?
Правильное «распознавание», когда следует нажимать CTRL+SHIFT+Enter, а когда просто Enter полностью зависит от понимания того, как работают массивы в формулах. Когда вы это поймете, сможете сказать, что конкретную формулу следует вводить (подтверждать) сочетанием клавиш – CTRL+SHIFT+Enter.
Конечно же, не подтвержденная, а просто как формула также может возвращать КАКОЙ-ТО результат (в чем вы могли только что убедиться сами). Однако, если вы сможете прочитать формулу и понять механизм, то вы заметите, что такой результат является ОШИБОЧНЫМ. И поэтому для правильной работы формулы вам необходимо ее подтвердить «Ctr+Shift+Enter». Как и все, понимание и использование формул массива требует практики. Тем не менее, стоит некоторое время посвятить тому, чтобы во всем разобраться. Потому что формулы массива позволяют решить многие проблемы, которые на первый взгляд могут казаться неразрешимыми.
Видео:Задачи с массивами | Pascal | Сумма и поиск элементовСкачать

Примеры вычислений и анализа формул массива
Каким образом можно просматривать и проверять значения промежуточных результатов расчета, например, содержание массивов, созданных в памяти компьютера и используемых для выполнения последующих действий? Ничего сложного! Пример 1:
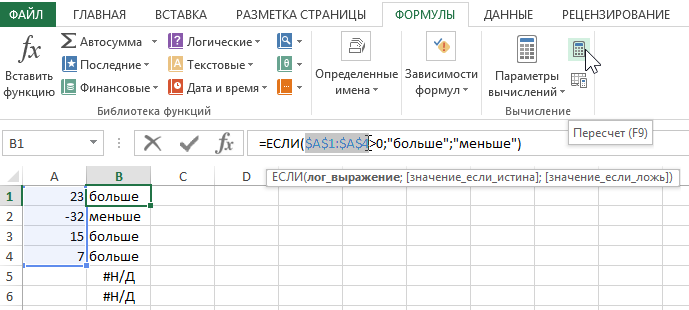
Перейдите на ячейку с формулой, а затем в строке формул выделите в первом аргументе функции ссылку на диапазон ячеек:
Нажмите клавишу F9 (или «Пересчет» в правом верхнем углу меню «Формулы»), и вы получите (в строке формулы) значения аргументов, которые используются для вычислений, как показано ниже:
— запись с использованием двоеточий означает, что мы имеем дело с элементами вертикального (столбикового) массива, элементы горизонтального (строкового) разделены стандартным символом — «;» (точкой с запятой).
Пример 2: Снова перейдите на ячейку с формулой массива, но на этот раз выделите первый аргумент функции целиком вместе со знаком сравнения «>» и значением критерия – «0»).
Нажмите кнопку F9, и вы получите массив результатов вычислений, как показано ниже:
То есть, созданный в памяти компьютера массив:
Пример 3: Выделите ячейку формулой массива где в функцию СУММ вложена функция ЕСЛИ. Затем в строке формул выберите весь аргумент функции СУММ (вместе с функцией ЕСЛИ):
Нажмите клавишу F9 и вы получите массив итоговых результатов вычисления, которые используются для суммирования, как показано ниже:
То есть, созданный в памяти компьютера массив:
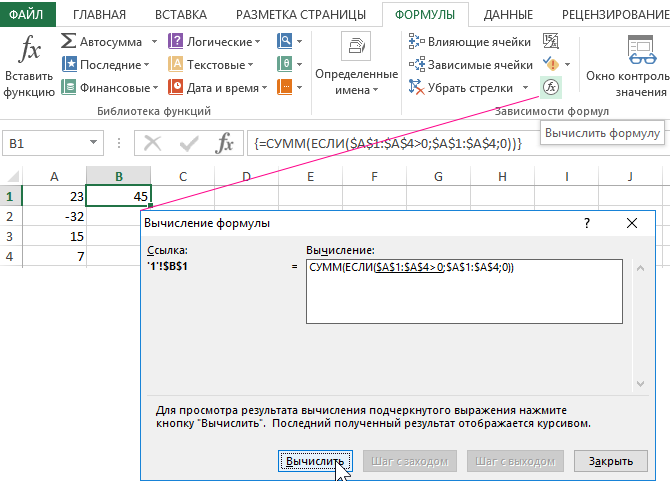
Пример 4: Просто перейдите на ячейку с формулой B1 и выберите инструмент «ФОРМУЛЫ»-«Зависимости формул»-«Вычислить формулу»
После чего нажмите на кнопку «Вычислить»:
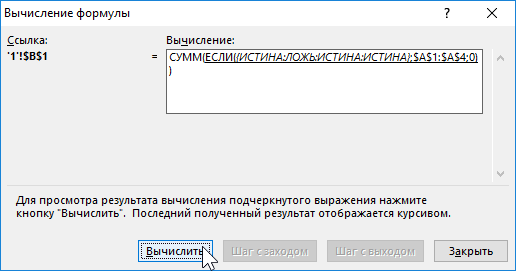
В результате ссылка на диапазон ячеек в аргументе вложенной функции ЕСЛИ разложилась на массив значений. Снова нажмите на кнопку «Вычислить»:
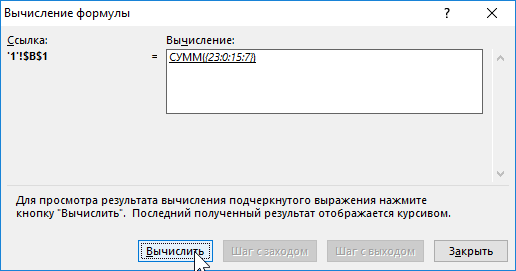
Мы получили массив значений теперь уже для функции СУММ. Такой же, как и в примере 3.
Часто неопытные пользователи Excel возмущаются, что формула не работает. В конце концов оказалось, как легко догадаться, формулу в массиве вводили как обычную (просто Enter). Речь идет не о недоразумении, которое произошло, а о том факте, что у этих пользователей возникает вопрос: как избегать таких ошибок? Поэтому важно сразу во всем разобраться, чтобы в дальнейшем больше не задавать таких вопросов.
Видео:MATLAB 04 Массивы и матрицыСкачать

Матричные уравнения
Рассмотрим матричное уравнение вида
где и — данные матрицы, имеющие одинаковое количество строк, причем матрица квадратная. Требуется найти матрицу , удовлетворяющую уравнению (4.5).
Теорема 4.2 о существовании и единственности решения матричного уравнения (4.5). Если определитель матрицы отличен от нуля, то матричное уравнение (4.5) имеет единственное решение .
В самом деле, подставляя в левую часть равенства (4.5), получаем , т.е. правую часть этого равенства.
Заметим, что решением матричного уравнения служит обратная матрица .
Рассмотрим также матричное уравнение вида
где и — данные матрицы, имеющие одинаковое количество столбцов, причем матрица квадратная. Требуется найти матрицу , удовлетворяющую уравнению (4.6).
Теорема 4.3 о существовании и единственности решения матричного уравнения (4.6). Если определитель матрицы отличен от нуля, то уравнение (4.6) имеет единственное решение .
Заметим, что матрица является как бы «левым» частным от «деления» матрицы на матрицу , поскольку матрица в (4.5) умножается на слева, а матрица — «правым» частным, так как матрица в (4.6) умножается на справа.
Пример 4.5. Даны матрицы
Решить уравнения: а) ; б) ; в) .
Решение. Обратная матрица была найдена в примере 4.2.
а) Решение уравнения находим, умножая обе его части слева на
б) Уравнение не имеет решений, так как матрицы и имеют разное количество столбцов .
в) Решение уравнения находим, умножая обе его части справа на
Пример 4.6. Решить уравнение: , где .
Решение. Преобразуя левую часть уравнения:
Следовательно, . Обратная матрица найдена в примере 4.2:
Пример 4.7. Решить уравнение , где
Решение. Обратные матрицы
были найдены в примерах 4.2, 4.3 соответственно. Решение уравнения находим по формуле
Пример 4.8. Решить уравнение , где
Решение. Определитель матрицы равен нулю, следовательно, обратная матрица не существует. Поэтому нельзя использовать формулу . Будем искать элементы матрицы . Подставляя в уравнение, получаем
Находим произведение, а затем приравниваем соответствующие элементы матриц в левой и правой частях уравнения:
Здесь, учитывая пропорциональность уравнений, в системе оставлены только два уравнения из четырех. Выразим неизвестные и
Следовательно, решение матричного уравнения имеет вид
💥 Видео
Язык Си для начинающих / #3 - Массивы данныхСкачать

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Составляем уравнение прямой по точкамСкачать

Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Solidworks. Уравнения в массивахСкачать

Как найти повторяющиеся элементы в массиве и скопировать их в другой массив(С++)?Скачать