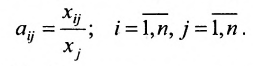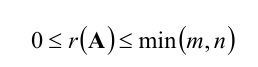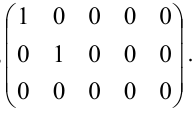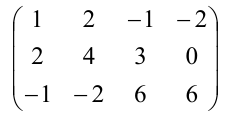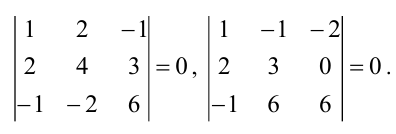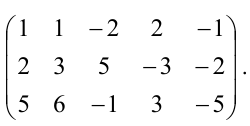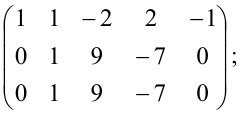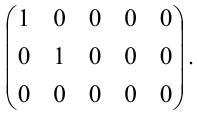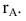Исследовать систему линейных агебраических уравнений (СЛАУ) на совместность означает выяснить, есть у этой системы решения, или же их нет. Ну и если решения есть, то указать сколько их.
Нам понадобятся сведения из темы «Система линейных алгебраических уравнений. Основные термины. Матричная форма записи». В частности, нужны такие понятия, как матрица системы и расширенная матрица системы, поскольку именно на них опирается формулировка теоремы Кронекера-Капелли. Как обычно, матрицу системы будем обозначать буквой $A$, а расширенную матрицу системы – буквой $widetilde$.
Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы системы, т.е. $rang A=rangwidetilde$.
Следствие из теоремы Кронекера-Капелли
Заметьте, что сформулированная теорема и следствие из неё не указывают, как найти решение СЛАУ. С их помощью можно лишь выяснить, существуют эти решения или нет, а если существуют – то сколько.
Исследовать СЛАУ $ left <begin& -3x_1+9x_2-7x_3=17;\ & -x_1+2x_2-4x_3=9;\ & 4x_1-2x_2+19x_3=-42. endright.$ на совместность. Если СЛАУ совместна, указать количество решений.
Чтобы выяснить наличие решений заданной СЛАУ, используем теорему Кронекера-Капелли. Нам понадобятся матрица системы $A$ и расширенная матрица системы $widetilde$, запишем их:
- Способ №1. Вычисление рангов по определению.
- Способ №2. Вычисление ранга методом элементарных преобразований.
- Ранг матрицы — определение и вычисление с примерами решения
- Определения
- Теоремы о ранге матриц. Свойства ранга матриц
- Определение системы m линейных уравнений с n неизвестными
- Экономические задачи, приводящие к системе линейных уравнений
- Определение ранга матрицы
- Вычисление ранга матрицы
- Метод окаймляющих миноров
- Исследование СЛАУ. Общие сведения
- Общие сведения (определения, условия, методы, виды)
- Ранг матрицы и его свойства
- 💡 Видео
Видео:Исследование систем линейных уравнений на совместностьСкачать

Способ №1. Вычисление рангов по определению.
Согласно определению, ранг – это наивысший порядок миноров матрицы, среди которых есть хоть один, отличный от нуля. Обычно исследование начинают с миноров первого порядка, но здесь удобнее приступить сразу к вычислению минора третьего порядка матрицы $A$. Элементы минора третьего порядка находятся на пересечении трёх строк и трёх столбцов рассматриваемой матрицы. Так как матрица $A$ содержит всего 3 строки и 3 столбца, то минор третьего порядка матрицы $A$ – это определитель матрицы $A$, т.е. $Delta A$. Для вычисления определителя применим формулу №2 из темы «Формулы для вычисления определителей второго и третьего порядков»:
$$ Delta A=left| begin -3 & 9 & -7 \ -1 & 2 & -4 \ 4 & -2 & 19 end right|=-21. $$
Итак, есть минор третьего порядка матрицы $A$, который не равен нулю. Минор четвёртого порядка составить невозможно, так как для него требуется 4 строки и 4 столбца, а в матрице $A$ всего 3 строки и 3 столбца. Итак, наивысший порядок миноров матрицы $A$, среди которых есть хотя бы один не равный нулю, равен 3. Следовательно, $rang A=3$.
Задача решена. Какие недостатки и преимущества имеет данный способ? Для начала поговорим о плюсах. Во-первых, нам понадобилось найти всего один определитель. После этого мы сразу сделали вывод о количестве решений. Обычно в стандартных типовых расчётах даются системы уравнений, которые содержат три неизвестных и имеют единственное решение. Для таких систем данный метод очень даже удобен, ибо мы заранее знаем, что решение есть (иначе примера не было бы в типовом расчёте). Т.е. нам остаётся только показать наличие решения наиболее быстрым способом. Во-вторых, вычисленное значение определителя матрицы системы (т.е. $Delta A$) пригодится после: когда станем решать заданную систему методом Крамера или с помощью обратной матрицы.
Однако метод вычисления ранга по определению нежелательно применять, если матрица системы $A$ является прямоугольной. В этом случае лучше применить второй метод, о котором пойдёт речь ниже. Кроме того, если $Delta A=0$, то мы ничего не сможем сказать о количестве решений заданной неоднородной СЛАУ. Может, СЛАУ имеет бесконечное количество решений, а может – ни одного. Если $Delta A=0$, то требуется дополнительное исследование, которое зачастую является громоздким.
Подводя итог сказанному, отмечу, что первый способ хорош для тех СЛАУ, у которых матрица системы квадратна. При этом сама СЛАУ содержит три или четыре неизвестных и взята из стандартных типовых расчетов или контрольных работ.
Видео:11. Ранг матрицыСкачать

Способ №2. Вычисление ранга методом элементарных преобразований.
Какие преимущества второго способа? Главное преимущество – это его универсальность. Нам совершенно неважно, является ли матрица системы квадратной или нет. Кроме того, мы фактически провели преобразования прямого хода метода Гаусса. Осталось лишь пару действий, и мы смогли бы получить решение данной СЛАУ. Честно говоря, второй способ нравится мне более первого, но выбор – это дело вкуса.
Ответ: Заданная СЛАУ совместна и определена.
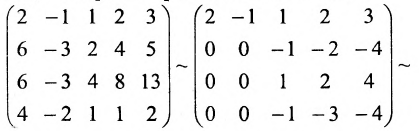
$$ left( begin 1 & -1 & 2 & -1\ -1 & 2 & -3 & 3 \ 2 & -3 & 5 & -4 \ 3 & -2 & 5 & 1 \ 2 & -1 & 3 & 2 end right) begin phantom\r_2+r_1\r_3-2r_1\ r_4-3r_1\r_5-2r_1endrightarrow left( begin 1 & -1 & 2 & -1\ 0 & 1 & -1 & 2 \ 0 & -1 & 1 & -2 \ 0 & 1 & -1 & 4 \ 0 & 1 & -1 & 4 end right) begin phantom\phantom\r_3-r_2\ r_4-r_2\r_5+r_2endrightarrow\ $$ $$ rightarrowleft( begin 1 & -1 & 2 & -1\ 0 & 1 & -1 & 2 \ 0 & 0 & 0 & 2 \ 0 & 0 & 0 & 2 \ 0 & 0 & 0 & 0 end right) begin phantom\phantom\phantom\ r_4-r_3\phantomendrightarrow left( begin 1 & -1 & 2 & -1\ 0 & 1 & -1 & 2 \ 0 & 0 & 0 & 2 \ 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 end right) $$
Расширенная матрица системы приведена к ступенчатому виду. Ранг ступенчатой матрицы равен количеству её ненулевых строк, поэтому $rangwidetilde=3$. Матрица $A$ (до черты) тоже приведена к ступенчатому виду, и ранг её равен 2, $rang=2$.
Ответ: система несовместна.
Приводим расширенную матрицу системы к ступенчатому виду:
$$ left( begin 2 & 0 & 7 & -5 & 11 & 42\ 1 & -2 & 3 & 0 & 2 & 17 \ -3 & 9 & -11 & 0 & -7 & -64 \ -5 & 17 & -16 & -5 & -4 & -90 \ 7 & -17 & 23 & 0 & 15 & 132 end right) overset<r_1leftrightarrow> $$ $$ rightarrowleft( begin 1 & -2 & 3 & 0 & 2 & 17\ 2 & 0 & 7 & -5 & 11 & 42\ -3 & 9 & -11 & 0 & -7 & -64\ -5 & 17 & -16 & -5 & -4 & -90 \ 7 & -17 & 23 & 0 & 15 & 132 end right) begin phantom\ r_2-2r_1 \r_3+3r_1 \ r_4+5r_1 \ r_5-7r_1 end rightarrow left( begin 1 & -2 & 3 & 0 & 2 & 17\ 0 & 4 & 1 & -5 & 7 & 8\ 0 & 3 & -2 & 0 & -1 & -13\ 0 & 7 & -1 & -5 & 6 & -5 \ 0 & -3 & 2 & 0 & 1 & 13 end right) begin phantom\ phantom\4r_3+3r_2 \ 4r_4-7r_2 \ 4r_5+3r_2 end rightarrow $$ $$ rightarrowleft( begin 1 & -2 & 3 & 0 & 2 & 17\ 0 & 4 & 1 & -5 & 7 & 8\ 0 & 0 & -11 & 15 & -25 & -76\ 0 & 0 & -11 & 15 & -25 & -76 \ 0 & 0 & 11 & -15 & 25 & 76 end right) begin phantom\ phantom\phantom \ r_4-r_3 \ r_5+r_2 end rightarrow left( begin 1 & -2 & 3 & 0 & 2 & 17\ 0 & 4 & 1 & -5 & 7 & 8\ 0 & 0 & -11 & 15 & -25 & -76\ 0 & 0 & 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 & 0 & 0 end right) $$
Мы привели расширенную матрицу системы и саму матрицу системы к ступенчатому виду. Ранг расширенной матрицы системы равен трём, ранг матрицы системы также равен трём. Так как система содержит $n=5$ неизвестных, т.е. $rangwidetilde=ranglt$, то согласно пункту №2 следствия из теоремы Кронекера-Капелли данная система является неопределённой, т.е. имеет бесконечное количество решений.
Ответ: система является неопределённой.
Во второй части мы разберём примеры, которые нередко включают в типовые расчёты или контрольные работы по высшей математике: исследование на совместность и решение СЛАУ в зависимости от значений параметров, входящих в неё.
Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Ранг матрицы — определение и вычисление с примерами решения
Содержание:
Элементарные преобразования матриц:
Рассмотрим прямоугольную матрицу:
состоящую из m строк и n столбцов. В п.3.2 отмсчалось, что каждую строку матрицы можно рассматривать как n-мсрный вектор, а каждый столбец — как m-мерный вектор. Тогда матрицу А можно записать в виде:
и, следовательно, данную матрицу можно рассматривать как систему вектор строк или вектор столбцов. Б указанных системах вектор-строк и вектор-столбцов можно выделять линейно независимые (зависимые) векторы. Тогда будем говорить, что строки (столбцы) матрицы линейно независимы (зависимы), если соответствующие им векторы независимы (зависимы).
Видео:Ранг матрицыСкачать

Определения
Определение: Рангом системы строк (соответственно столбцов) матрицы А называется наибольшее число линейно независимых среди них.
Поскольку легко доказать, что ранг системы строк матрицы равен рангу системы её столбцов, то справедливо следующее
Определение: Рангом матрицы, обозначаемым r(А), называется максимальное число линейно независимых строк (столбцов) матрицы.
При транспонировании матрицы ранг её не изменяется.
Другой метод определения ранга матрицы связан с понятием определителя.
Выделим в матрице А любые k строк и k столбцов. Элементы, стоящие на их пересечении, образуют квадратную матрицу, определитель которой называется минором k-го порядка матрицы А. Ясно, что величина к должна удовлетворять двум условиям: 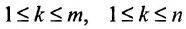
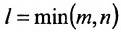
Определение: Рангом матрицы, обозначаемым r(А), называется порядок самого старшего минора этой матрицы, не равного нулю.
Из определения следует, что если ранг матрицы А равен l, то среди всех её миноров существует хотя бы один минор l-го порядка, отличный от нуля, но все миноры (l+1)-го порядков либо равны нулю, либо не могут быть составлены.
Вычисление ранга матрицы путём перебора всех её миноров весьма трудоёмко. Существует, однако, более простой способ вычисления ранга матрицы, основанный на упрощении структуры матрицы с помощью элементарных преобразований. Элементариыми преобразованиями матрицы называют следующие преобразования:
- обмен местами двух строк или двух столбцов матрицы;
- умножение всех элементов строки или столбца матрицы на произвольное число
, не равное нулю;
- прибавление ко всем элементам строки (столбца) матрицы соответствующих элементов другой строки (столбца), предварительно умноженных на одно и то же число;
- исключение из матрицы строки или столбца, состоящего из нулей.
Матрицы называются эквивалентными, если от одной из них к другой можно перейти путём конечного числа элементарных преобразований.
Ступенчатой матрицей называется матрица, удовлетворяющая тому свойству, что если в какой-либо из сё строк первый отличный от нуля элемент стоит на l-м месте, то во всех следующих строках на первых l местах стоят нули:
где элементы 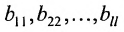
Для вычисления ранга матрицы приводят её с помощью цепочки элементарных преобразований к ступенчатому виду. Тогда ранг матрицы совпадает с числом её ненулевых диагональных элементов.
Теоремы о ранге матриц. Свойства ранга матриц
Относительно ранга матриц можно сформулировать следующие теоремы:
Теорема: Если матрица имеет минор порядка r, отличный от нуля, для которого все содержащие его миноры порядка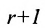
Вычисление ранга матрицы при помощи метода окаймления нужно вести от низших порядков к высшим. Сначала ищем минор первого порядка (т.е. элемент матрицы) или сразу второго порядка, отличный от нуля. Затем вычисляем окаймляющие его миноры следующего порядка, пока не найдём среди них отличного от нуля и т.д., пока не найдем минор порядка l, отличный от нуля, для которого либо все окаймляющие его миноры порядка l+1 равны нулю, либо такие миноры не могут быть составлены.
Теорема: Элементарные преобразования не меняют ранга матрицы.
Доказательство теоремы следует из определения ранга матрицы и свойств определителей.
Пример:
Найти ранг матрицы:
Решение:
Минор первого порядка в левом верхнем углу равен 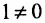
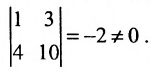
Значит ранг матрицы равен 2.
Пример:
Найти ранг матрицы:
Решение:
При помощи элементарных преобразований приведём данную матрицу к ступенчатому виду. На первом шаге умножим последовательно первую строку на 3, 3, 2 и вычтем из второй, третьей, четвёртой строк соответственно:
В эквивалентной матрице прибавим к третьей строке вторую и вычтем вторую из четвёртой строки:
(поменяем местами третью и четвертую строки)
(поменяем местами третий, четвёртый и пятый столбцы со вторым и опустим строки, состоящие из нулей) 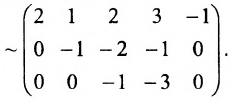
Отмстим некоторые свойства ранга матриц.
- Ранг суммы двух (или нескольких) матриц не больше суммы их рангов.
- Любую матрицу ранга r можно представить в виде суммы r матриц ранга 1, но нельзя представить в виде суммы менее чем r таких матриц.
- Любую матрицу С ранга r можно представить в виде произведения
, где А состоит из r линейно независимых столбцов, г B -из r линейно независимых строк.
- Ранг произведения матриц порядка n удовлетворяет неравенству
.
Определение системы m линейных уравнений с n неизвестными
Системой m линейных уравнений с n неизвестными 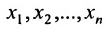
Числа 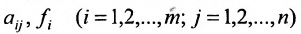
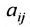
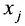
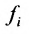
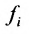
С помощью знака суммирования 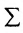
составленная из коэффициентов системы 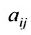
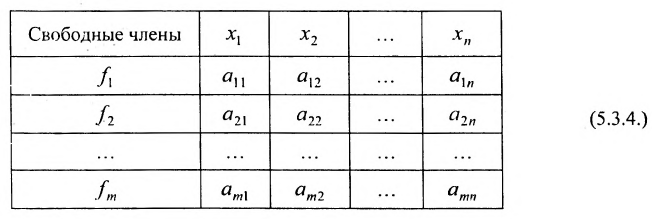
системы. Если к этой матрице добавить столбец свободных членов, то получим расширенную матрицу системы: 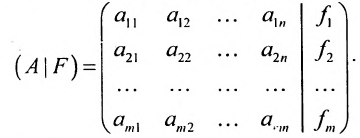
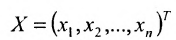
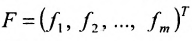

Используется также табличная форма записи системы (5.3.1):
Отметим, что (5.3.1), (5.3.2), (5.3.3), (5.3.4)- различные виды записи одной и той же системы линейных уравнений.
Решением системы (5.3.1) называется любой упорядоченный набор действительных чисел 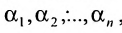
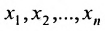
Система уравнений (5.3.1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений. Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
Две системы уравнений с одинаковыми наборами неизвестных 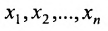
Отмстим, что для любой системы (5.3.1) возможны только три случая:
- система (5.3.1) имеет единственное решение;
- система (5.3.1) имеет бесчисленное множество решений;
- система (5.3.1) несовместна.
Множество всех решений системы (5.3.1) называется ее общим решением.
Решить систему (5.3.1) — значит найти ее общее решение.
Пример:
Пусть задана система
Тогда эту систему можно записать в матричном виде:
или в виде таблицы:
Система определенная, так как она имеет единственное решение 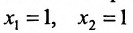
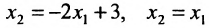
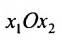
Экономические задачи, приводящие к системе линейных уравнений
Предположим, что производственные мощности для изготовления n различных видов продукции установлены в т цехах. Пусть 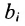
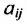
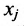
Широкий круг задач экономики приводит к составлению системы уравнений. Так в примере 4.3.2 составлялась система линейных уравнений (4.3.1) балансовой модели для трёх отраслей. В общем случае под балансовой моделью понимается система уравнений, каэ/сдое из которых выражает требование баланса между производимым количеством продукции и совокупной потребностью в этой продукции.
При построении балансовых моделей используется понятие чистой (или технологической) отрасли, т.е. условной отрасли, объединяющей всё производство данного продукта независимо от ведомственной (административной) подчинённости и форм собственности предприятий и фирм. Всё народное хозяйство представляется в виде совокупности п отраслей, каждая из которых рассматривается как производящая и как потребляющая.
Если обозначить через:
— межотраслевые потоки продукции, где i и j — соотвестственно номера отраслей производящих и потребляющих;
— валовой выпуск продукции i-й отрасли;
— конечную продукцию i-Й отрасли,
;
— количество продукции i-й отрасли, учитывая только прямые затраты, необходимые для производства единицы продукции j-й отрасли,
то систему уравнений баланса можно записать в виде:
или в матричной форме:
где Х- вектор-столбец валовой продукции; Y- вектор-столбец конечной продукции; А — матрица коэффициентов прямых затрат.
Основу экономико-математической модели межотраслевого баланса составляет технологическая матрица А, содержащая коэффициенты прямых затрат на производство единицы продукции:
Коэффициент. прямых затрат являются довольно стабильной величиной во времени.
Переписав матричное уравнение (5.4.2) в виде EX-AX = Y или (E-A)X = Y, (5.4.3) получим стандартную форму записи системы уравнений.
Видео:Как найти ранг матрицы (пример) - bezbotvyСкачать

Определение ранга матрицы
Рассмотрим прямоугольную матрицу (4.1). Если в этой матрице выделить произвольно 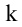
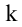
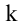
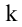
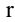
Очевидно, что выполняется соотношение
Ранг матрицы находится либо методом окаймления миноров, либо методом элементарных преобразований. При вычислении ранга матрицы первым способом следует переходить от миноров низших порядков к минорам более высокого порядка. Если уже найден минор D 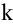
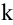
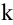
Элементарными называются следующие преобразования матрицы:
- перестановка двух любых строк (или столбцов),
- умножение строки (или столбца) на отличное от нуля число,
- прибавление к одной строке (или столбцу) другой строки (или столбца), умноженной на некоторое число.
Две матрицы называются эквивалентными, если одна из них получается из другой с помощью конечного множества элементарных преобразований.
Эквивалентные матрицы не являются, вообще говоря, равными, но их ранги равны. Если матрицы А и В эквивалентны, то это записывается так: А
Канонической матрицей называется матрица, у которой в начале главной диагонали стоят подряд несколько единиц (число которых может равняться нулю), а все остальные элементы
равны нулю, например,
При помощи элементарных преобразований строк и столбцов любую матрицу можно привести к канонической. Ранг канонической матрицы равен числу единиц на ее главной диагонали.
Пример:
Найти методом окаймления миноров ранг матрицы
Решение:
Начинаем с миноров 1-го порядка, т.е. с элементов матрицы А. Выберем, например, минор (элемент) 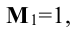
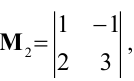
Переходим теперь к минорам 3-го порядка, окаймляющим 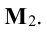
Таким образом, асе окаймляющие миноры третьего порядка оказались равными нулю. Ранг матрицы А равен двум.
Пример:
Найти ранг матрицы 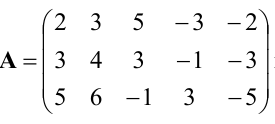
Решение:
Из второй строки вычтем первую и переставим эти строки:
Теперь из второй и третьей строк вычтем первую, умноженную соответственно на 2 и 5:
из третьей строки вычтем первую; получим матрицу 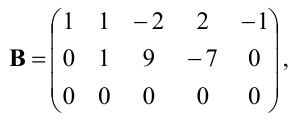
Видео:Найти ранг матрицы при всех значениях параметраСкачать

Вычисление ранга матрицы
Для исследования разрешимости систем линейных уравнений важную роль играет понятие ранга матрицы. Рассмотрим прямоугольную матрицу А
Выделим k произвольных строк и k произвольных столбцов этой матрицы. Определитель k-го порядка, составленный из элементов матрицы А, расположенных на пересечении выделенных строк и столбцов, называется минором k-го порядка матрицы А.
Рангом матрицы А называется наибольший порядок ее миноров, отличных от нуля. Обозначение: rank А,
Базисным минором матрицы называется всякий отличный от нуля ее минор, порядок которого равен рангу матрицы.
Рассмотрим некоторые методы вычисления ранга матрицы.
Метод окаймляющих миноров
Минор порядка k+1, содержащий в себе минор порядка k, называется окаймляющим минором.
Вычисляя ранг матрицы, удобнее переходить от миноров меньших порядков к минорам больших порядков. Если найден минор k-го порядка, отличный от нуля, а все окаймляющие его миноры порядка k+1 равны нулю, то ранг матрицы равен k.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Определители второго и третьего порядков и их свойства
- Метод Гаусса — определение и вычисление
- Прямая линия на плоскости и в пространстве
- Плоскость в трехмерном пространстве
- Кратный интеграл
- Ряды в математике
- Дифференциальные уравнения с примерами
- Обратная матрица — определение и нахождение
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Урок 1. Матрицы, определитель матрицы и ранг матрицы | Высшая математика | TutorOnlineСкачать

Исследование СЛАУ. Общие сведения
В данной статье мы расскажем о методах, видах, условиях и определениях исследований решений систем линейных уравнений, что такое метод Кронекера-Капели, а также приведем примеры.
Видео:Линейная алгебра, 6 урок, Ранг матрицыСкачать

Общие сведения (определения, условия, методы, виды)
Системы линейных алгебраических уравнений с n неизвестными могут иметь:
- единственное решение;
- бесконечное множество решение (неопределенные СЛАУ);
- ни одного решения (несовместные СЛАУ).
Пример 1
Система x + y + z = 1 2 x + 2 y + 2 z = 3 не имеет решений, поэтому она несовместна.
Система x + y = 1 2 x + 7 y = — 3 имеет единственное решение x = 2 ; y = 1 .
Система x + y = 1 2 x + 2 y = 2 3 x + 3 y = 3 имеет бесконечное множество решений x = t y = 1 — t при — ∞ t ∞ .
Перед решением системы уравнений необходимо исследовать систему, т.е. ответить на следующие вопросы:
- Совместна ли система?
- Если система совместна, то, какое количество решений она имеет — одно или несколько?
- Как найти все решения?
Если система малоразмерна при m = n , то ответить на поставленные вопросы можно при помощи метода Крамера:
- если основной определитель системы, то система совместна и имеет единственное решение, которое вычисляется методом Крамера;
- если, и один из вспомогательных определителей, то система не является совместной, т.е. не имеет решений;
- если и все, и один из коэффициентов СЛАУ, то система не является определенной и имеет бесконечное множество решений.
Видео:Теорема Кронекера-КапеллиСкачать

Ранг матрицы и его свойства
Бывают случаи, которые выбиваются из представленных вариантов решения СЛАУ, например, линейные уравнения с большим количеством уравнений и неизвестных.
Для такого варианта решения существует ранг матрицы, который представляет собой алгоритм действий в случае решения системы матрицы, когда
В математике выделяют следующие подходы к определению ранга матрицы:
- при помощи понятия линейной зависимости/независимости строк/столбцов матрицы. Ранг равен максимальному количеству независимых строк (столбцов) матрицы
- при помощи понятия минора матрицы в качестве наивысшего порядка минора, который отличается от нуля. Минор матрицы порядка k — определитель k-го порядка, составленный из элементов, которые стоят на пересечении вычеркиваемых k-строк и k-столбцов матрицы;
- при помощи метода Гаусса. По завершении прямого хода ранг матрицы равняется количеству ненулевых строк.
Обозначение ранга матрицы: r ( A ) , r g ( A ) , r A .
Свойства ранга матрицы:
- квадратная невырожденная матрица обладает рангом, который отличается от нуля;
- если транспонировать матрицу, то ранг матрицы не изменяется;
- если поменять местами 2 параллельные строки или 2 параллельных столбца, ранг матрицы не изменяется;
- при удалении нулевого столбца или строки ранг матрицы не изменяется;
- ранг матрицы не изменяется, если удалить строку или столбец, которые являются линейной комбинацией других строк;
- при умножении все элементов строки/столбца на число k н е р а в н о н у л ю ранг матрицы не изменяется;
- ранг матрицы не больше меньшего из ее размеров: r ( А ) ≤ m i n ( m ; n ) ;
- когда все элементы матрицы равны нулю, то только тогда r ( A ) = 0 .
Пример 2
А 1 = 1 1 1 2 2 2 3 3 3 , B 1 = 1 0 0 0 0 0
r ( A 1 ) = 1 , r ( B 1 ) = 1
А 2 = 1 2 3 4 0 5 6 7 0 0 0 0 ; В 2 = 1 1 3 1 2 1 4 3 1 2 5 0 5 4 13 6
💡 Видео
Ранг матрицыСкачать

15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Система линейных уравнений. Общее решение. Метод ГауссаСкачать

Лекция 13. Исследование систем линейных уравнений. Теорема Кронекера — Капелли.Скачать

Решение системы уравнений методом Крамера.Скачать

Математика Без Ху!ни. Система линейных уравнений. Метод Крамера.Скачать

Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Решение системы уравнений методом ГауссаСкачать

ФСР. Система однородных уравнений. Общее решениеСкачать

12. Метод Гаусса решения систем линейных уравнений. Часть 1.Скачать


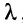 , не равное нулю;
, не равное нулю;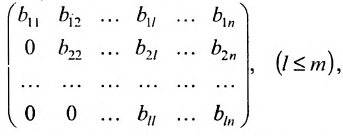
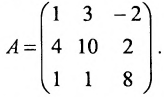
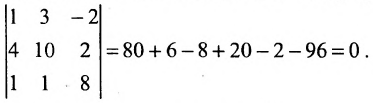



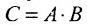 , где А состоит из r линейно независимых столбцов, г B -из r линейно независимых строк.
, где А состоит из r линейно независимых столбцов, г B -из r линейно независимых строк.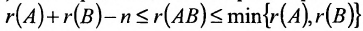 .
.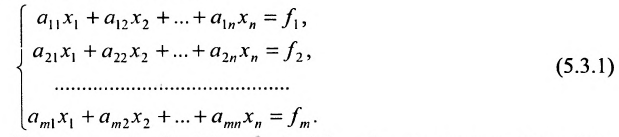

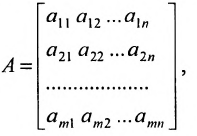
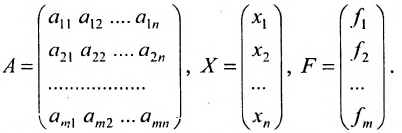
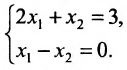
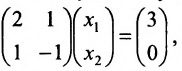

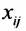 — межотраслевые потоки продукции, где i и j — соотвестственно номера отраслей производящих и потребляющих;
— межотраслевые потоки продукции, где i и j — соотвестственно номера отраслей производящих и потребляющих;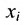 — валовой выпуск продукции i-й отрасли;
— валовой выпуск продукции i-й отрасли; 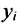 — конечную продукцию i-Й отрасли,
— конечную продукцию i-Й отрасли, 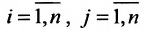 ;
;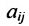 — количество продукции i-й отрасли, учитывая только прямые затраты, необходимые для производства единицы продукции j-й отрасли,
— количество продукции i-й отрасли, учитывая только прямые затраты, необходимые для производства единицы продукции j-й отрасли,