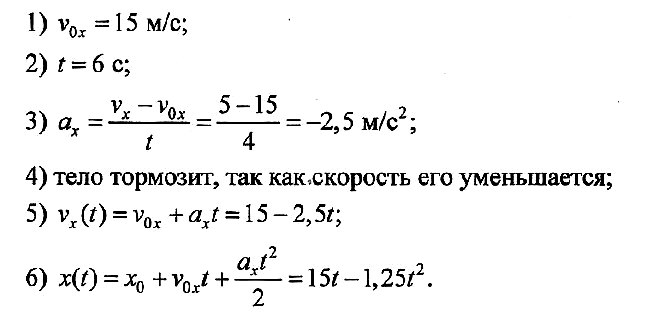Как определить проекцию ускорения тела по уравнению

теория по физике 🧲 кинематика

• Равноускоренное прямолинейное движение — движение по прямой линии с постоянным ускорением ( a =const).
• Ускорение — векторная физическая величина, показывающая изменение скорости тела за 1 с. Обозначается как a .
• Единица измерения ускорения — метр в секунду в квадрате (м/с 2 ).
• Акселерометр — прибор для измерения ускорения.

Формула ускорения

Ускорение тела равно отношению изменения вектора скорости ко времени, в течение которого это изменение произошло:

v — скорость тела в данный момент времени, v ₀ — скорость тела в начальный момент времени, t — время, в течение которого изменялась скорость

Пример №1. Состав тронулся с места и через 20 секунд достиг скорости 36 км/ч. Найти ускорение его разгона.

Сначала согласуем единицы измерения. Для этого переведем скорость в м/с: умножим километры на 1000 и поделим на 3600 (столько секунд содержится в 1 часе). Получим 10 м/с.

Начальная скорость состава равно 0 м/с, так как изначально он стоял на месте. Имея все данные, можем подставить их в формулу и найти ускорение:

Проекция ускорения

v_x — проекция скорости тела в данный момент времени, v_0x — проекция скорости в начальный момент времени, t — время, в течение которого изменялась скорость

Знак проекции ускорения зависит от того, в какую сторону направлен вектор ускорения относительно оси ОХ:

• Если вектор ускорения направлен в сторону оси ОХ, то его проекция положительна.
• Если вектор ускорения направлен в сторону, противоположную направлению оси ОХ, его проекция отрицательная.

При решении задач на тему равноускоренного прямолинейного движения проекции величин можно записывать без нижнего индекса, так как при движении по прямой тело изменяет положение относительно только одной оси (ОХ). Их обязательно нужно записывать, когда движение описывается относительно двух и более осей.

Направление вектора ускорения

Направление вектора ускорения не всегда совпадает с направлением вектора скорости!

Равноускоренным движением называют такое движение, при котором скорость за одинаковые промежутки времени изменяется на одну и ту же величину. При этом направления векторов скорости и ускорения тела совпадают ( а ↑↑ v ).

Равнозамедленное движение — частный случай равноускоренного движения, при котором скорость за одинаковые промежутки времени уменьшается на одну и ту же величину. При этом направления векторов скорости и ускорения тела противоположны друг другу ( а ↑↓ v ).

Пример №2. Автомобиль сначала разогнался, а затем затормозил. Во время разгона направления векторов его скорости и ускорения совпадают, так как скорость увеличивается. Но при торможении скорость уменьшается, потому что вектор ускорения изменил свое направление в противоположную сторону.

Видео:Физика - перемещение, скорость и ускорение. Графики движения.Скачать

График ускорения

График ускорения — график зависимости проекции ускорения от времени. Проекция ускорения при равноускоренном прямолинейном движении не изменяется (a_x=const). Графиком ускорения при равноускоренном прямолинейном движении является прямая линия, параллельная оси времени.

Зависимость положения графика проекции ускорения относительно оси ОХ от направления вектора ускорения:

• Если график лежит выше оси времени , движение равноускоренное (направление вектора ускорения совпадает с направлением оси ОХ). На рисунке выше тело 1 движется равноускорено.
• Если график лежит ниже оси времени , движение равнозамедленное (вектор ускорения направлен противоположно оси ОХ). На рисунке выше тело 2 движется равнозамедлено.

Если график ускорения лежит на оси времени, движение равномерное, так как ускорение равно 0. Скорость в этом случае — величина постоянная.

Чтобы сравнить модули ускорений по графикам, нужно сравнить степень их удаленности от оси времени независимо от того, лежат они выше или ниже нее. Чем дальше от оси находится график, тем больше его модуль. На рисунке график 2 находится дальше от оси времени по сравнению с графиком один. Поэтому модуль ускорения тела 2 больше модуля ускорения тела 1.

Пример №3. По графику проекции ускорения найти участок, на котором тело двигалось равноускорено. Определить ускорение в момент времени t₁ = 1 и t₂ = 3 с.

В промежуток времени от 0 до 1 секунды график ускорения рос, с 1 до 2 секунд — не менялся, а с 2 до 4 секунд — опускался. Так как при равноускоренном движении ускорение должно оставаться постоянным, ему соответствует второй участок (с 1 по 2 секунду).

Чтобы найти ускорение в момент времени t, нужно мысленно провести перпендикулярную прямую через точку, соответствующую времени t. От точки пересечения с графиком нужно мысленно провести перпендикуляр к оси проекции ускорения. Значение точки, в которой пересечется перпендикуляр с этой осью, покажет ускорение в момент времени t.

В момент времени t₁ = 1с ускорение a = 2 м/с 2 . В момент времени t₂ = 3 ускорение a = 0 м/с 2 .

На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.

К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.

Алгоритм решения

1. Определить, какому типу движения соответствует график зависимости координаты тела от времени.
2. Определить величины, которые характеризуют такое движение.
3. Определить характер изменения величин, характеризующих это движение.
4. Установить соответствие между графиками А и Б и величинами, характеризующими движение.

Решение

График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:

Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.

График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.

График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.

Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.

График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».

График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

1. Записать исходные данные.
2. Записать формулу, связывающую известные из условия задачи величины.
3. Выразить из формулы искомую величину.
4. Вычислить искомую величину, подставив в формулу исходные данные.

Решение

Запишем исходные данные:

• Начальная скорость v₀ = 5 м/с.
• Конечная скорость v = 15 м/с.
• Пройденный путь s = 40 м.

Формула, которая связывает ускорение тела с пройденным путем:

Так как скорость растет, ускорение положительное, поэтому перед ним в формуле поставим знак «+».

Выразим из формулы ускорение:

Подставим известные данные и вычислим ускорение автомобиля:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Внимательно прочитайте текст задани я и выберите верный ответ из списка. На рисунке приведён график зависимости проекции скорости тела v_x от времени.

Какой из указанных ниже графиков совпадает с графиком зависимости от времени проекции ускорения этого тела a_x в интервале времени от 6 с до 10 с?

Алгоритм решения

1. Охарактеризовать движение тела на участке графика, обозначенном в условии задачи.
2. Вычислить ускорение движение тела на этом участке.
3. Выбрать график, который соответствует графику зависимости от времени проекции ускорения тела.

Решение

Согласно графику проекции скорости в интервале времени от 6 с до 10 с тело двигалось равнозамедленно. Это значит, что проекция ускорения на ось ОХ отрицательная. Поэтому ее график должен лежать ниже оси времени, и варианты «а» и «в» заведомо неверны.

Чтобы выбрать между вариантами «б» и «г», нужно вычислить ускорение тела. Для этого возьмем координаты начальной и конечной точек рассматриваемого участка:

• t₁ = 6 с. Этой точке соответствует скорость v₁ = 0 м/с.
• t₂ = 10 с. Этой точке соответствует скорость v₂ = –10 м/с.

Используем для вычислений следующую формулу:

Подставим в нее известные данные и сделаем вычисления:

Этому значению соответствует график «г».

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

1. Записать формулу ускорения.
2. Записать формулу для вычисления модуля ускорения.
3. Выбрать любые 2 точки графика.
4. Определить для этих точек значения времени и проекции скорости (получить исходные данные).
5. Подставить данные формулу и вычислить ускорение.

Решение

Записываем формулу ускорения:

По условию задачи нужно найти модуль ускорения, поэтому формула примет следующий

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Выбираем любые 2 точки графика. Пусть это будут:

• t₁ = 1 с. Этой точке соответствует скорость v₁ = 15 м/с.
• t₂ = 2 с. Этой точке соответствует скорость v₂ = 5 м/с.

Подставляем данные формулу и вычисляем модуль ускорения:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Видео:ЕГЭ по физике. Задание 1. Определение проекции ускоренияСкачать

Кинематика

Механика — это раздел физики, изучающий механическое движение тел.

Кинематика — это раздел механики, в котором изучается механическое движение тел без учета причин, вызывающих это движение.

Материальная точка — тело, обладающее массой, размерами которого в данной задаче можно пренебречь, если

• расстояние, которое проходит тело, много больше его размера;
• расстояние от данного тела до другого тела много больше его размера;
• тело движется поступательно.

Система отсчета — это тело отсчета, связанная с ним система координат и прибор для измерения времени.
Траектория — это линия, которую описывает тело при своем движении.
Путь — это скалярная величина, равная длине траектории.
Перемещение — это вектор, соединяющий начальное положение тела с его конечным положением за данный промежуток времени.

Важно!
В процессе движения путь может только увеличиваться, а перемещение как увеличиваться, так и уменьшаться, например, когда тело поворачивает обратно.
При прямолинейном движении в одном направлении путь равен модулю перемещения, а при криволинейном — путь больше перемещения.
Перемещение на замкнутой траектории равно нулю.

Основная задача механики — определить положение тела в пространстве в любой момент времени.

Видео:Как найти проекцию вектора скорости и ускорения. Выполнялка 112Скачать

Механическое движение и его виды

Механическое движение — это изменение положения тела в пространстве относительно других тел с течением времени.

Механическое движение может быть:
1. по характеру движения

• поступательным — это движение, при котором все точки тела движутся одинаково и любая прямая, мысленно проведенная в теле, остается параллельна сама себе;
• вращательным — это движение, при котором все точки твердого тела движутся по окружностям, расположенным в параллельных плоскостях;
• колебательным — это движение, которое повторяется в двух взаимно противоположных направлениях;

2. по виду траектории

• прямолинейным — это движение, траектория которого прямая линия;
• криволинейным — это движение, траектория которого кривая линия;

• равномерным — движение, при котором скорость тела с течением времени не изменяется;
• неравномерным — это движение, при котором скорость тела с течением времени изменяется;

• равноускоренным — это движение, при котором скорость тела увеличивается с течением времени на одну и ту же величину;
• равнозамедленным — это движение, при котором скорость тела уменьшается с течением времени на одну и ту же величину.

Видео:Физика-9. "График проекции скорости"Скачать

Относительность механического движения

Относительность движения — это зависимость характеристик механического движения от выбора системы отсчета.

Правило сложения перемещений

Перемещение тела относительно неподвижной системы отсчета равно векторной сумме перемещения тела относительно подвижной системы отсчета и перемещения подвижной системы отсчета относительно неподвижной системы отсчета:

где ​ ( S ) ​ — перемещение тела относительно неподвижной системы отсчета;
​ ( S_1 ) ​ — перемещение тела относительно подвижной системы отсчета;
​ ( S_2 ) ​ — перемещение подвижной системы отсчета относительно неподвижной системы отсчета.

Правило сложения скоростей

Скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной системы отсчета:

где ​ ( v ) ​ — скорость тела относительно неподвижной системы отсчета;
​ ( v_1 ) ​ — скорость тела относительно подвижной системы отсчета;
​ ( v_2 ) ​ — скорость подвижной системы отсчета относительно неподвижной системы отсчета.

Относительная скорость

Важно! Чтобы определить скорость одного тела относительно другого, надо мысленно остановить то тело, которое мы принимаем за тело отсчета, а к скорости оставшегося тела прибавить скорость остановленного, изменив направление его скорости на противоположное.

Пусть ( v_1 ) — скорость первого тела, а ( v_2 ) — скорость второго тела.
Определим скорость первого тела относительно второго ( v_ ) :

Определим скорость второго тела относительно первого ( v_ ) :

Следует помнить, что траектория движения тела и пройденный путь тоже относительны.

Если скорости направлены перпендикулярно друг к другу, то относительная скорость рассчитывается по теореме Пифагора:

Если скорости направлены под углом ​ ( alpha ) ​ друг к другу, то относительная скорость рассчитывается по теореме косинусов:

Видео:ОПРЕДЕЛЕНИЕ ПРОЕКЦИИ УСКОРЕНИЯ ПО ГРАФИКУ ПРОЕКЦИИ СКОРОСТИ| ФИЗИКА| ПОДГОТОВКА К ЕГЭ| ЗАДАНИЕ 1.Скачать

Скорость

Скорость — это векторная величина, характеризующая изменение перемещения данного тела относительно тела отсчета с течением времени.

Обозначение — ​ ( v ) ​, единицы измерения — ​м/с (км/ч)​.

Средняя скорость — это векторная величина, равная отношению всего перемещения к промежутку времени, за которое это перемещение произошло:

Средняя путевая скорость — это скалярная величина, равная отношению всего пути, пройденного телом, к промежутку времени, за которое этот путь пройден:

Важно! Чтобы определить среднюю скорость на всем участке пути, надо время разделить на отдельные промежутки и все время представить в виде суммы этих промежутков.
Чтобы определить среднюю скорость за все время движения, надо путь разделить на отдельные участки и весь путь представить как сумму этих участков.

Мгновенная скорость — это скорость тела в данный момент времени или в данной точке траектории.
Мгновенная скорость направлена по касательной к траектории движения.

Видео:Урок 18 (осн). Координаты тела. График движения. График скоростиСкачать

Ускорение

Ускорение – это векторная физическая величина, характеризующая быстроту изменения скорости.

Обозначение — ​ ( a ) ​, единица измерения — м/с 2 .
В векторном виде:

где ​ ( v ) ​ – конечная скорость; ​ ( v_0 ) ​ – начальная скорость;
​ ( t ) ​ – промежуток времени, за который произошло изменение скорости.

В проекциях на ось ОХ:

где ​ ( a_n ) ​ – нормальное ускорение, ​ ( a_ ) ​ – тангенциальное ускорение.

Тангенциальное ускорение сонаправлено с вектором линейной скорости, а значит, направлено вдоль касательной к кривой:

Нормальное ускорение перпендикулярно направлению вектора линейной скорости, а значит, и касательной к кривой:

Ускорение характеризует быстроту изменения скорости, а скорость – векторная величина, которая имеет модуль (числовое значение) и направление.

Важно!
Тангенциальное ускорение характеризует быстроту изменения модуля скорости. Нормальное ускорение характеризует быстроту изменения направления скорости.
Если ( a_ ) ≠ 0, ( a_n ) = 0, то тело движется по прямой;
если ( a_ ) = 0, ( a_n ) = 0, ​ ( v ) ​ ≠ 0, то тело движется равномерно по прямой;
если ( a_ ) = 0, ( a_n ) ≠ 0, тело движется равномерно по кривой;
если ( a_ ) = 0, ( a_n ) = const, то тело движется равномерно по окружности;
если ( a_ ) ≠ 0, ( a_n ) ≠ 0, то тело движется неравномерно по окружности.

Видео:Расчет ускорения по графикуСкачать

Равномерное движение

Равномерное движение – это движение, при котором тело за любые равные промежутки времени совершает равные перемещения.

Скорость при равномерном движении – величина, равная отношению перемещения к промежутку времени, за которое это перемещение произошло:

Проекция вектора скорости на ось ОХ:

Проекция вектора скорости на координатную ось равна быстроте изменения данной координаты:

График скорости (проекции скорости)

График скорости (проекции скорости) представляет собой зависимость скорости от времени:

График скорости при равномерном движении – прямая, параллельная оси времени.
График 1 лежит над осью ​ ( t ) ​, тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ​ ( t ) ​, тело движется против оси ОХ.

Перемещение при равномерном движении – это величина, равная произведению скорости на время:

Проекция вектора перемещения на ось ОХ:

График перемещения (проекции перемещения)

График перемещения (проекции перемещения) представляет собой зависимость перемещения от времени:

График перемещения при равномерном движении – прямая, выходящая из начала координат.
График 1 лежит над осью ( t ) , тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ( t ) , тело движется против оси ОХ.

По графику зависимости скорости от времени можно определить перемещение, пройденное телом за время ( t ) . Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).

Координата тела при равномерном движении рассчитывается по формуле:

График координаты представляет собой зависимость координаты от времени: ​ ( x=x(t) ) ​.

График координаты при равномерном движении – прямая.
График 1 направлен вверх, тело движется по направлению оси ОХ:

График 2 параллелен оси ОХ, тело покоится.
График 3 направлен вниз, тело движется против оси ОХ:

Видео:На рисунке приведён график зависимости проекции Vx скорости тела от времени t - №22677Скачать

Прямолинейное равноускоренное движение

Прямолинейное равноускоренное движение – это движение по прямой, при котором тело движется с постоянным ускорением:

При движении с ускорением скорость может как увеличиваться, так и уменьшаться.

Скорость тела при равноускоренном движении рассчитывается по формуле:

При разгоне (в проекциях на ось ОХ):

При торможении (в проекциях на ось ОХ):

График ускорения (проекции ускорения) при равноускоренном движении представляет собой зависимость ускорения от времени:

График ускорения при равноускоренном движении – прямая, параллельная оси времени.
График 1 лежит над осью t, тело разгоняется, ​ ( a_x ) ​ > 0.
График 2 лежит под осью t, тело тормозит, ( a_x ) ( v_ ) ​ > 0, ​ ( a_x ) ​ > 0.

График 2 направлен вниз, тело движется равнозамедленно в положительном направлении оси ОХ, ( v_ ) > 0, ( a_x ) ( v_ ) ( a_x ) ( t_2-t_1 ) ​. Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).

Перемещение при равноускоренном движении рассчитывается по формулам:

Перемещение в ​ ( n ) ​-ую секунду при равноускоренном движении рассчитывается по формуле:

Координата тела при равноускоренном движении рассчитывается по формуле:

Видео:Решение графических задач на равномерное движениеСкачать

Свободное падение (ускорение свободного падения)

Свободное падение – это движение тела в безвоздушном пространстве под действием только силы тяжести.

Все тела при свободном падении независимо от массы падают с одинаковым ускорением, называемым ускорением свободного падения.
Ускорение свободного падения всегда направлено к центру Земли (вертикально вниз).

Обозначение – ​ ( g ) ​, единицы измерения – м/с 2 .

Важно! ( g ) = 9,8 м/с 2 , но при решении задач считается, что ( g ) = 10 м/с 2 .

Движение тела по вертикали

Тело падает вниз, вектор скорости направлен в одну сторону с вектором ускорения свободного падения:

Если тело падает вниз без начальной скорости, то ​ ( v_0 ) ​ = 0.
Время падения рассчитывается по формуле:

Тело брошено вверх:

Если брошенное вверх тело достигло максимальной высоты, то ​ ( v ) ​ = 0.
Время подъема рассчитывается по формуле:

Движение тела, брошенного горизонтально

Движение тела, брошенного горизонтально, можно представить как суперпозицию двух движений:

1. равномерного движения по горизонтали со скоростью ​ ( v_0=v_ ) ​;
2. равноускоренного движения по вертикали с ускорением свободного падения ​ ( g ) ​ и без начальной скорости ​ ( v_=0 ) ​.

Скорость тела в любой момент времени:

Угол между вектором скорости и осью ОХ:

Движение тела, брошенного под углом к горизонту (баллистическое движение)

Движение тела, брошенного под углом к горизонту, можно представить как суперпозицию двух движений:

1. равномерного движения по горизонтали;
2. равноускоренного движения по вертикали с ускорением свободного падения.

Скорость тела в любой момент времени:

Угол между вектором скорости и осью ОХ:

Время подъема на максимальную высоту:

Максимальная высота подъема:

Максимальная дальность полета:

Важно!
При движении вверх вертикальная составляющая скорости будет уменьшаться, т. е. тело вдоль вертикальной оси движется равнозамедленно.
При движении вниз вертикальная составляющая скорости будет увеличиваться, т. е. тело вдоль вертикальной оси движется равноускоренно.
Скорость ​ ( v_0 ) ​, с которой тело брошено с Земли, будет равна скорости, с которой оно упадет на Землю. Угол ​ ( alpha ) ​, под которым тело брошено, будет равен углу, под которым оно упадет.

При решении задач на движение тела, брошенного под углом к горизонту, важно помнить, что в точке максимального подъема проекция скорости на ось ОУ равна нулю:

Это облегчает решение задач:

Видео:Физика - уравнения равноускоренного движенияСкачать

Движение по окружности с постоянной по модулю скоростью

Движение по окружности с постоянной по модулю скоростью – простейший вид криволинейного движения.

Траектория движения – окружность. Вектор скорости направлен по касательной к окружности.
Модуль скорости тела с течением времени не изменяется, а ее направление при движении по окружности в каждой точке изменяется, поэтому движение по окружности – это движение с ускорением.
Ускорение, которое изменяет направление скорости, называется центростремительным.
Центростремительное ускорение направлено по радиусу окружности к ее центру.

Центростремительное ускорение – это ускорение, характеризующее быстроту изменения направления вектора линейной скорости.
Обозначение – ​ ( a_ ) ​, единицы измерения – ​м/с 2​ .

Движение тела по окружности с постоянной по модулю скоростью является периодическим движением, т. е. его координата повторяется через равные промежутки времени.
Период – это время, за которое тело совершает один полный оборот.
Обозначение – ​ ( T ) ​, единицы измерения – с.

где ​ ( N ) ​ – количество оборотов, ​ ( t ) ​ – время, за которое эти обороты совершены.
Частота вращения – это число оборотов за единицу времени.
Обозначение – ​ ( nu ) ​, единицы измерения – с –1 (Гц).

Период и частота – взаимно обратные величины:

Линейная скорость – это скорость, с которой тело движется по окружности.
Обозначение – ​ ( v ) ​, единицы измерения – м/с.
Линейная скорость направлена по касательной к окружности:

Угловая скорость – это физическая величина, равная отношению угла поворота к времени, за которое поворот произошел.
Обозначение – ​ ( omega ) ​, единицы измерения – рад/с .

Направление угловой скорости можно определить по правилу правого винта (буравчика).
Если вращательное движение винта совпадает с направлением движения тела по окружности, то поступательное движение винта совпадает с направлением угловой скорости.
Связь различных величин, характеризующих движение по окружности с постоянной по модулю скоростью:

Важно!
При равномерном движении тела по окружности точки, лежащие на радиусе, движутся с одинаковой угловой скоростью, т. к. радиус за одинаковое время поворачивается на одинаковый угол. А вот линейная скорость разных точек радиуса различна в зависимости от того, насколько близко или далеко от центра они располагаются:

Если рассматривать равномерное движение двух сцепленных тел, то в этом случае одинаковыми будут линейные скорости, а угловые скорости тел будут различны в зависимости от радиуса тела:

Когда колесо катится равномерно по дороге, двигаясь относительно нее с линейной скоростью ​ ( v_1 ) ​, и все точки обода колеса движутся относительно его центра с такой же линейной скоростью ( v_1 ) , то относительно дороги мгновенная скорость разных точек колеса различна.

Мгновенная скорость нижней точки ​ ( (m) ) ​ равна нулю, мгновенная скорость в верхней точке ​ ( (n) ) ​ равна удвоенной скорости ​ ( v_1 ) ​, мгновенная скорость точки ​ ( (p) ) ​, лежащей на горизонтальном радиусе, рассчитывается по теореме Пифагора, а мгновенная скорость в любой другой точке ​ ( (c) ) ​ – по теореме косинусов.

Видео:График проекции ускоренияСкачать

Как определить проекцию ускорения тела по уравнению

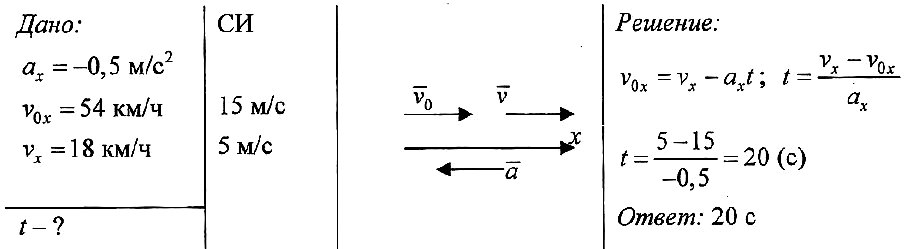
Задача № 1. Автомобиль, двигаясь с ускорением –0,5 м/с 2 , уменьшил свою скорость от 54 до 18 км/ч. Сколько времени ему для этого понадобилось?

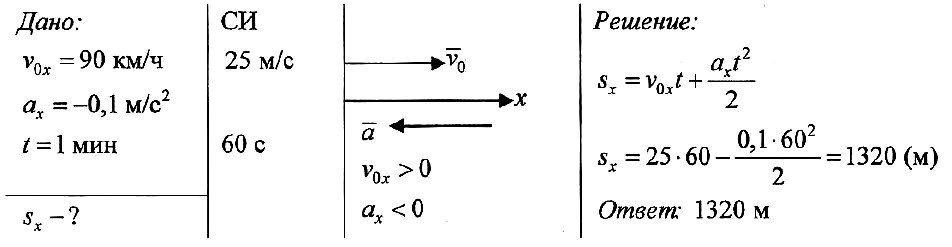
Задача № 2. При подходе к станции поезд начал торможение с ускорением 0,1 м/с 2 , имея начальную скорость 90 км/ч. Определите тормозной путь поезда, если торможение длилось 1 мин.

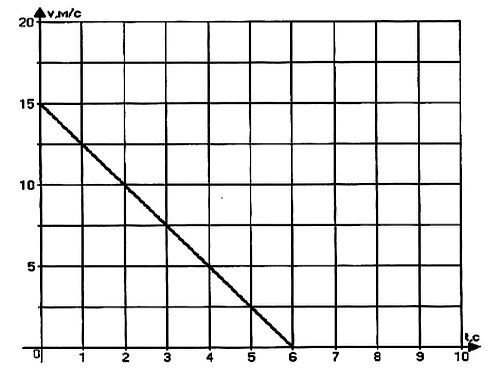
Задача № 3. По графику проекции скорости определите: 1) начальную скорость тела; 2) время движения тела до остановки; 3) ускорение тела; 4) вид движения (разгоняется тело или тормозит); 5) запишите уравнение проекции скорости; 6) запишите уравнение координаты (начальную координату считайте равной нулю).

Решение:

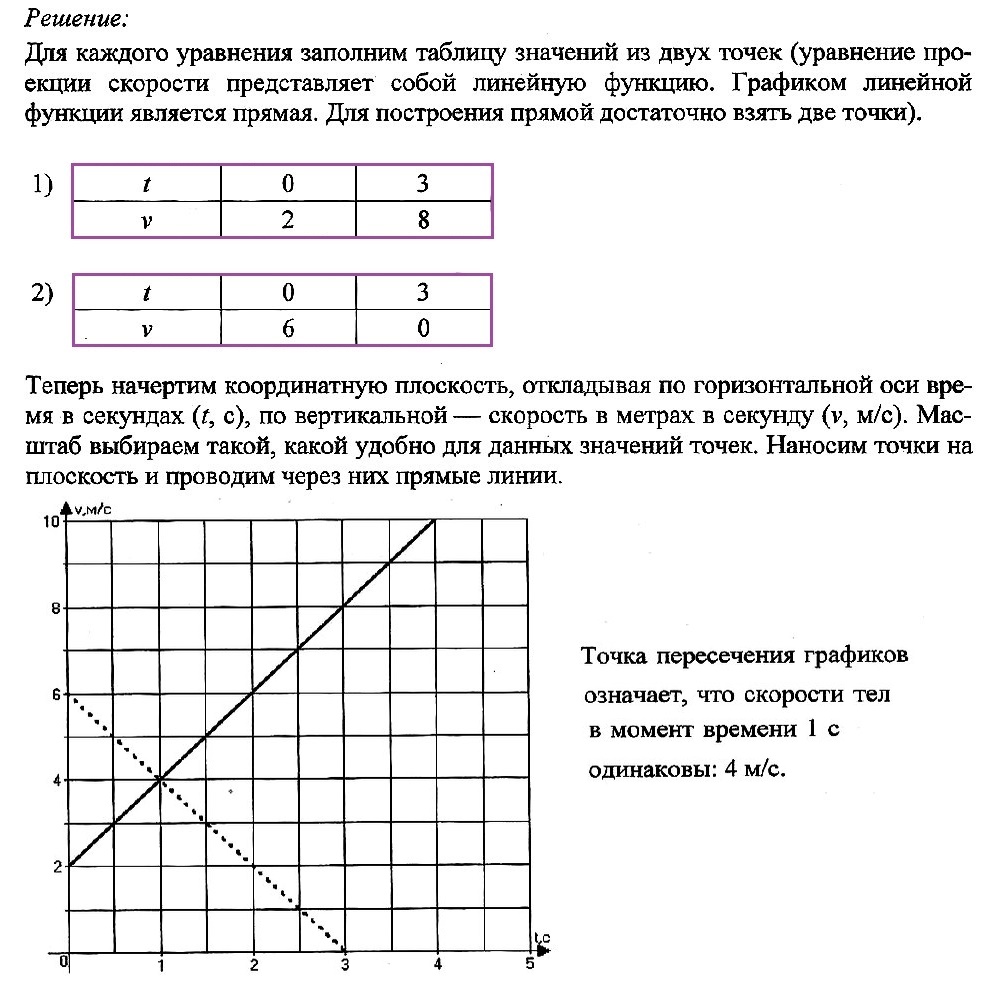
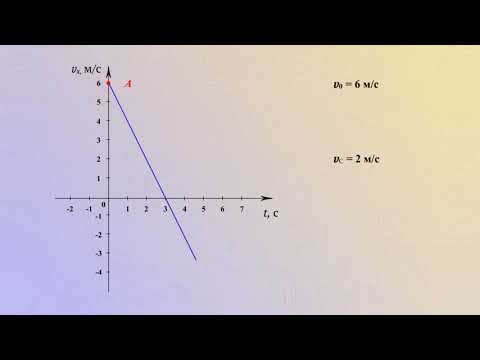
Задача № 4. Движение двух тел задано уравнениями проекции скорости:
v_1x(t) = 2 + 2t
v_2x(t) = 6 – 2t
В одной координатной плоскости постройте график проекции скорости каждого тела. Что означает точка пересечения графиков?

Задача № 5. Движение тела задано уравнением x(t) = 5 + 10t — 0,5t 2 . Определите: 1) начальную координату тела; 2) проекцию скорости тела; 3) проекцию ускорения; 4) вид движения (разгоняется тело или тормозит); 5) запишите уравнение проекции скорости; 6) определите значение координаты и скорости в момент времени t = 4 с . Сравним уравнение координаты в общем виде с данным уравнением и найдем искомые величины.

Решение:

Задача № 6. Вагон движется равноускоренно с ускорением -0,5 м/с 2 . Начальная скорость вагона равна 54 км/ч. Через сколько времени вагон остановится? Постройте график зависимости скорости от времени.

Задача № 7. Самолет, летевший прямолинейно с постоянной скоростью 360 км/ч, стал двигаться с постоянным ускорением 9 м/с 2 в течение 10 с в том же направлении. Какой скорости достиг самолет и какое расстояние он пролетел за это время? Чему равна средняя скорость за время 10 с при ускоренном движении?

Задача № 8. Трамвай двигался равномерно прямолинейно со скоростью 6 м/с, а в процессе торможения — равноускоренно с ускорением 0,6 м/с 2 . Определите время торможения и тормозной путь трамвая. Постройте графики скорости v(t) и ускорения a(t).

Задача № 9. Тело, имея некоторую начальную скорость, движется равноускоренно. За время t = 2 с тело прошло путь S = 18 м , причём его скорость увеличилась в 5 раз. Найти ускорение и начальную скорость тела.

Задача № 10. (повышенной сложности) Прямолинейное движение описывается формулой х = –4 + 2t – t 2 . Опишите движение, постройте для него графики v_x(t), s_x(t), l(t) .

Задача № 11. ОГЭ Поезд, идущий со скоростью v₀ = 36 км/ч , начинает двигаться равноускоренно и проходит путь S = 600 м , имея в конце этого участка скорость v = 45 км/ч . Определить ускорение поезда а и время t его ускоренного движения.

Краткое пояснение для решения
ЗАДАЧИ на Прямолинейное равноускоренное движение.

Равноускоренным движением называется такое движение, при котором тело за равные промежутки времени изменяет свою скорость на одну и ту же величину. Движение, при котором скорость равномерно уменьшается, тоже считают равноускоренным (иногда его называют равнозамедленным).

Величины, участвующие в описании равноускоренного движения, почти все векторные. При решении задач формулы записывают обычно через проекции векторов на координатные оси. Если тело движется по горизонтали, ось обозначают буквой х, если по вертикали — буквой у.

Если векторы скорости и ускорения сонаправлены (их проекции имеют одинаковые знаки), тело разгоняется, т. е. его скорость увеличивается. Если же векторы скорости и ускорения противоположно направлены, тело тормозит.

Это конспект по теме «ЗАДАЧИ на Прямолинейное равноускоренное движение с решениями». Выберите дальнейшие действия:

29 Комментарии

«отрицательного ускорения» не бывает. Если движущееся тело снижает скорость-вступает в силу 3-й Закон Ньютона: F/m равно, или больше S/tt. Ньютон пытался уравнять ускорения S/tt и F/m, но ошибка в формуле S=att/2 не позволяла . Ошибку эту он сделал, когда искал ускорение свободного падения «яблока…» Конечная скорость-(9,8…) это НЕ at! at-это СРЕДНЯЯ скорость! Она равна (0+V конечная)/2.
V средняя=at. Vконечная=2at. S=(0+2at)/2*t. S=att (и-НИКАКИХ «/2)!
…..Если тело весом (массой) m кг., прошло путь S за время t, то ускорения S/tt=F/m. Искать просто ускорение- бессмысленно. Оно должно помочь найти S,t,F,m,V… Задача: камень весом 25 кг. передвинули на 40 м. за минуту. Вопрос: какую приложили силу- (F) ?
Решение: 40/3600=F/25. Ответ: 0,28 км.м/с. («крутящий момент»)
Задача: этот-же камень, с таким-же «упорством» тащили …100 м. Вопрос: t ? Решение: 100/tt=0,28/25. Ответ: 1,5 минуты (95 секунд).
«Законы» Ньютона пора пересмотреть… (при равномерном движении — НЕТ ускорения. А СРЕДНЯЯ скорость? А из неё и находим ускорение!)
При решении задач нельзя отнимать «скорость от скорости». Всякое движение -это энергия и время. И то и другое не может иметь знак «-«. Время не может пойти «вспять». И =Энергия. Она или есть, или её нет. S/tt=F/m -это значит, материя со временем переходит в энергию, а энергия со временем переходит в материю. ПРИРОДА- ВЕЧНА !

Спасибо за альтернативную точку зрения, не указанную в школьных учебниках физики. Надеюсь, это поможет учащимся расширить свой кругозор в области физики.

Ускорение — это вектор, а он отрицательным быть не может. Но вот проекция ускорения очень даже может быть отрицательной. И, прямо скажем, я не пойму что Вы тут написали, но попахивает каким-то бредом. Хотя бы потому, что at — это приращение скорости, а средняя скорость — это перемещение деленное на время движения, или путь на время движения, если интересует средняя ПУТЕВАЯ скорость. Деление же на 2, в уравнении движения возникает из-за правил интегрирования, которые говорят о том, что интеграл at по dt равен 0.5at^2/

«если тело прошло путь S за время t — график движения НЕ влияет ни на СРЕДНЮЮ скорость, ни на ускорение». А это значит, что не всегда «а» изменяет. скорость. При равномерном движении «а» такое-же, как и при любом движении, потому -что «Ускорение»- это ЭНЕРГИЯ, затраченная на движение, и она эквивалентна изменению скорости. S/tt. Будем считать, что это изменение скорости. Но F/m- это ЭНЕРГИЯ ! И она влияет на изменение скорости, измеряется так-же: «м/сек.сек.»
При решении задач на движение надо движение перевести в СРЕДНЮЮ скорость. А из НЕЁ и искать «ускорение».
У «яблока…» V нач.=0, V конеч.=9,8 м/с. V средняя=(0+9,8):2 V ср.=4,9 м/сек. S=V средняя (!)*t. 4,9*1=4,9 м.
«СРЕДНЯЯ скорость»-это «at». (при любом графике движения). «Конечная» скорость =2at. S=(0+2at)/2*t. S=a*tt, или at*t.
Задачка:… V нач.=10 м/с. V кон.=50 м/с. t=10 секунд. S=? a=? Решение:
Грубейшая ошибка: найти «а» : (50-10)/10. «а»=4 м/сек.сек. S=a*tt. 4*100=400 м.
Правильно будет так: (10+50)/2=30 м/с. Это-СРЕДНЯЯ скорость.. «а»=30/10. а=3 м/сек.сек. S=: V ср.*t=300 м. ; а*tt. 3*100=300 м S/tt=F/m. Ньютон ДОЛЖЕН был вывести такую формулу, но из-за ошибки «att/2» не смог…. S=a*tt = (at*t).
(не «заморачивай-те» головы студентов интегралами).

S/tt=F/m.
Как связаны эти половинки равенства? Обратите внимание на поиск «а» через F и m .
Задачка: машина m=1165 кг. Мощность мотора= 75 л.с. («Москвич», «Жигули»).
Вопрос: за сколько секунд машина наберёт скорость 100 км/час.
За какое время машина максимально быстро пройдёт 150 м, 250 м., 400 м.
Какую скорость наберёт за 10 сек, за 15 сек., за 25 сек.?
Решение: F/m=a. кпд двс=16%. 75 л.с=5625 кг.м/с 16% будет: 5625/6,25=900 кг.м/сек. Это 12 л.с. (при 100% кпд) a=F/m. 900/1165=0,77 м/сек.сек. Это «ускорение» F/m — «ЭНЕРГИЯ движения»
Скорость 100 км/час (27,7 м/с машина набирает за 18 сек.) a=V средняя/t. 13,9/18=0,77 м/сек.сек. «УСКОРЕНИЕ ОДИНАКОВО и через ЭНЕРГИЮ «at» и через «прибавку скорости к скорости»
-скорость машины через 10 сек.: V кон.=2at. 2*0,77*10=15,4 м/с. 55,5 км/час.
———————————— 15 сек.: 2*0,77*15=23,1 м/с 83,2 км/час.
————————————25 сек.: 2*0,77*25=38,5 м/сек. 138,6 км/ч.
максимальную скорость 153 км/час машины наберут за: 42,5/0,77=55,2 сек.
S=att. 10 c. S=0,77*10*10=77 м
15 с. S=173,25 м
25 с. S=481,25 м
За 55,2 сек. машина проедет: 0,77*55,2*55,2=2346 м.
Обратите внимание: V конечная=2at (a НЕ at); S=att (a НЕ att/2 !)
Вывод: «Ускорение»-это ЭНЕРГИЯ движения (м/сек.сек.) РАВНАЯ ЧИСЛЕННО «прибавке скорости к скорости» S/tt, Vср./t
———: с помощью «а» надо искать F. S,v,t можно измеритью

а что это за ошибка att/2? и Почему это ошибка вы доказали верность теорий энергий , но не ошибочности att/2. Я думаю нужно обьяснить я сам плох в физике поэтому описал как смог.

Тело движется прямолинейно под действием постоянной силы 12 Н, при этом зависимость координаты тела от времени имеет вид: (м). Определить: массу тела; импульс тела в момент времени t = 2 c ; среднюю скорость за промежуток времени от t1 = 0 c до t2 = 2 c.

S/tt=F/m. S=? Тело двигалось,или стояло?

при решении задач на «рав. дв. с начальной скоростью больше (или меньше 0) искать «а» надо со ВСЕГО пути,а не только с момента V о.
…Если машина прошла 100 км. и только один раз ускорилась в течении 10 сек., то это не значит, что она израсходовала бензин только на разгон.
Даже в космосе, в невесомости.она она когда-нибудь остановилась, постепенно СНИЖАЯ скорость. Значит: её движение- НЕ РАВНОмерное.
Если-бы она продолжала двигаться равномерно, её «ускорение»-ЭНЕРГИЯ движения-снизилась бы в t квадрат раз: (а=10 м/сс…а=0,1 м/сс…а=0,0000……м/сек.сек…..) Задачка:
V нач.=10 м/с. «а»=2 м/сек.сек. t=5 сек. S-? «а»=?
Решение: ….(если будем рассматривать «а» только с момента нарастания скорости, то «а» не надо искать. Оно=2 м/сек.сек. А,вот, на ВЕСЬ путь ускорение будет другим: a=S/tt. (без 2S !). h (V конечная) «треугольника»=2at. 2*2*5=20 м/сек. ОБЩАЯ конечная скорость=10+20.
Получилась ТРАПЕЦИЯ, площадь которой-(путь)= (v+v+2at)/2*t. (10+10+20)/2*5. S=100 м. «а»=100/25=4 м/сек.сек. (или считать V ср./t
20/5=4 м/сек.сек.
НЕ ЗАБЫВАЙ-ТЕ и НЕ ПУТАЙ-ТЕ: at- это СРЕДНЯЯ скорость . 2at- это КОНЕЧНАЯ скорость. (при V нач.=0) И ещё: СРЕДНЯЯ скорость и ускорение НЕ зависят от графика движения тела! СРЕДНЯЯ скорость-это «равномерное движение». Скорость at-это то-же РАВНОМЕРНОЕ движение, V нач.=V конечной.. Если нач.и кон. скорости НЕ равны- это НЕ скорость at, и НЕ средняя скорость….
…Ошибка в формуле S=att/2 привела к этой «белеберде», к «интегралам». S/t=at, a at*t=2S (!?). «яблоко…» : 4,9/1=4,9. 4,9/1=9,8 ?!
S,t.m…можно ИЗМЕРИТЬ. Задача-найти F ! S/tt=F/m. Вот таким должен был быть труд Ньютона. НО ошибка «/2….»

….мощность мотора при условиях в задаче. (вес машины…1200 кг)
..машина имела ускорение 4 м/сс.. (для машины-«приличное» ускорение..) F/1200=4 сек.сек. F=4800 кг м./сек. Это=64 л.с. при 100% КПД
КПД ДВС=16 %. 64*6,25=400 л.с. (есть такие моторы. Правда, вес ТАКИХ машин 2,5-3 тонны…) Вот пример «теории и практики». А если вес машины …2650 кг., то мотор должен быть: 4*2650/75*6,25=883 л.с.

Определить тормозную путь,если известны начальная скорость 30 м/сек и замедление 6 м/сек2

V кон.=2at. 30=2*6*t. t=2,5 c. S=att. 6*2,5*2,5. S=37,5 м.

В 1-ой задаче (про самолёт): Vконечная=Vo+2at. V кон.=1008 км/час.
Путь(S)= (Vo+at)*t. (100+9*10)*10. S=1900 м. (если искать по площади трапеции, : (Vo+Vo+2at)/2*t. (200+180)/2*10. S=1900 м.
«а» «общее»= S/tt. 1900/100=19 м/сек.сек. При таком «ускорении» скорость через 30 сек.будет: 19*900=61560 км/ч .
«ускорение» 9 м/сек.сек.-это уже 2 раза превышает ускорение «яблока…». ….а ускорение 19 м/сс в течении 10 сек. (думаю)человек не перенесёт

В последней задаче: t= V ср./ a. Vср.=15 м/с. t=15/6=2,5 секунды (быстрее свободного падения…) S=att. 6*2,5*2/5=37,5 м.

(…напутал в решении…)
При «ускорении» 19 м/сс, скорость через 30 сек. будет: Vкон.=2at. 2*19*30. V кон.=1140 м/с. (4104 км/час)

задача № 11. V o=10. V кон.=12,5. S=600. a=? t=?
Решение: S=(v+V)/2*t. 600=11,25*t. t=53,3..сек. Всё верно ! А.вот, ускорение будет другим: a=S/tt. 600/53,3/53,3=0,21 м/сек.сек.
проверка: S=att. 0,21*53,3*53,3=600. (если S=att/2, то S=300 м. , а «ускорение» -? a=(V-v)/t (?), 2s/tt (?)… a=S/tt, или V средняя/t !
И ещё: почему при решении задач с разными нач.и кон. скоростями вместо трапеции рисуют какие-то «чёрточки со стрелками, и каким-то «ящичком » ? ПЛОЩАДЬ трапеции -это ПУТЬ. S=(V+V)/2*t ! Значения НЕ имеет, какая скорость больше: нач., или конечная : (v+V)/2, или (V+v)2, потому, что ДВИЖЕНИЕ-это ЭНЕРГИЯ*t. «at » at при любом графике движения ЕСТЬ (и равна) СРЕДНЕЙ СКОРОСТИ. Все вычисления надо делать из СРЕДНЕЙ скорости! ( S=at/2*t ? a=(v-V)/t ?)

во второй задаче: V нач.=25 м/с. а=0,1 м/сс. t=60 c. S=? (давать надо одно: или «ускорение», или «время»)
решение: S=V ср.*t. 12,5*60=750 м. «ускорение»= V ср./t. 12,5/60. t=0,2 м/сс.
При «а»=0,1 м/сс. t=Vср./a. 12,5/0,1=125 секунд.
S при а=0,2 м/сс. S=att. 0,208*60*60=750 м. (и при разгоне, и при торможении)
S при а=0,1 м/сс. S=att. 0,1/125*125. S=1562,5 м. (и при разгоне. и при торможении)

задачка: Vo=0. V коечная=0 (как в жизни, на практике). S=100 м. t=5 c. «а»=?
Решение: a=S/tt. 100:25=4 м/сс.
2). Vo=0. V кон.=40. t=5 c. S=100 м. «а»=?
Решение: a=(0+40)/2t. a=4 м/сс.
3). Vo=40. V кон.=0. S=100. t=5. «а»=? Ответ: «а»=4 м/сс
4) Vo=20. V кон.=20. S=100. t=5. «а»=? Решение: а=V СРЕДНЯЯ !/t. (20+20)/2t. a=4 м/сс
Вывод: «ГРАФИК ДВИЖЕНИЯ НЕ влияет на СРЕДНЮЮ СКОРОСТЬ и УСКОРЕНИЕ (если S и t- НЕИЗМЕННЫ!)

задача № 9
V нач.=х. V кон.=5х. V ср.=3х. t=2c. S=18 м. V ср.=9 м. х=9/3=3 м/с. V кон.=15 м/с.
a=S/tt=Vср./t a=18/4=9/2=4,5 м/сс
ПРОВЕРКА: S=att. 4,5*2*2=18 м.
Проверка (по Вашему решению): a=6 м/сс. S=att/2. 6*2*2/2=12 м (?)

У Вас не получается, потому что Вы проверяете ответ по своей формуле. Правильная формула проекции перемещения указана в начале статьи и в самой задаче!

Товарищ Иван, не вводите в заблуждение других людей, если почитали СТО и решили, что в силах пересмотреть законы Ньютона, то для начала почитайте и ОТО и СТО повнимательней, а то от вашего бреда даже глаза слезятся… То, что вы приводите в качестве аргументов — оными не является, т.к доказательной базы кроме придуманных вами расчетов — 0, т.е. нет, т.е. вообще нет, от слова совсем. Плюсом могу добавить, что подобный «контент» не рассматривается на таком уровне (9 класс) , т.к. у детей от чрезмерных уточнений в области физики поедет крыша. Все это больше напоминает поговорку: «Заставь дурака молиться — он себе лоб расшибет». Удачи в научных изысканиях ( с уважением и без сарказма).

Вот такие «анонимы» в средневековье … всех, кто думал не так, как «принято». (текст изменен модератором сайта)

Во второй задаче некорректная формулировка. По факту, даны избыточные данные. «Тормозной путь» соответствует расстоянию до полной остановки, то есть такое понятие подразумевает конечную скорость, равную нулю. А по заданным числам конечная скорость будет равна v0 — a * t = 25 — 0.1*60 = 19 м/c.

Возможно, конкретно в это задаче автор подразумевал под тормозным путём участок, на котором поезд замедлял движение, при этом не до полной остановки. Меня это тоже вначале сбило с толку.

V нач.=25 м/с. t=60 c. V кон.=0. V кон. (от 0 до 25м/с, или ОТ 25 м/с ДО «0»- БЕЗ РАЗНИЦЫ !) V СРЕДНЯЯ (12,5)=at. t=60 c. a=12,5/60=0,2 м/сс
При ТАКОМ изменении скорости S=att. 0,2*60*60=750 м.
При «замедлении» (или наращивании) скорости) =0,1 м/сс S=att. 0,1*60*60=360 м. Но, при а=0,1 м/сс за 60 сек. V кон.=2at. 2*0,1*60=12 м/с
Т.Е.: Если-бы начальная скорость была=12 м/с, ускорение=0,1 м/сс, то через 60 с. поезд прошёл-бы 360 м. и ОСТАНОВИЛСЯ.
До остановки поезда при «замедлении»= 0,1 м/сс со скорости 25 м/с надо: V кон.=2at. 25=2*0,1*t. t=125 сек.
750 м. при замедлении о,1 м/сс tt=750/a. t=86,6 секунды.
Что-бы не было такой «путаницы» НЕ надо давать в условии задачи вместе V,S,t,a .
(Даша! V нач.-это МГНОВЕННАЯ скорость. А скорость at- это СРЕДНЯЯ (постоянная,равномерная) скорость. ТАК нельзя отнимать.

В 11-й задаче проще использовать формулу a = (V-Vo) / t

Даша! V конечная (при равно-ускоренном движении и одной из скоростей=0 ) есть 2at. СРЕДНЯЯ скорость (25+0)/2=12,5 м/с. С такой СРЕДНЕЙ скоростью поезд за минуту (60 сек) пройдёт: 12,5*60=750 м.
Если задачу решать через «а», то t=12,5/0,1=125 секунд. S=V ср.*t. 12,5*125=1562,5 м.
Если поезд (по условию задачи) прошёл 750 м. (до остановки), то его ЗАМЕДЛЕНИЕ скорости (-«а»): S=att 750/60/60. а=0,2 м/сс.
Вывод: давать в условии задачи одно: или «а», или t

Добрый день. Задача №2. Почему ax= -0/1, а не 0,1?

С точки зрения физики торможение — это тоже ускорение, только с обратным знаком. Поменяли условие задачи № 2, чтобы не было двусмысленности.

всем доброго времени.
Очень е силен в физике последние лет 25, по этой причине прошу помочь в решении некой задачи!
Дано начальная скорость = 10 м/с.
Вопрос сможет ли тело долететь до высоты 4 м и если сможет то с какой скоростью. Да, полет вертикальный!
На мой взгляд в даны не все условия, но могу и ошибаться.
Спасибо.

Такие задачи рассматриваются в разделе «Задачи на свободное падение» https://uchitel.pro/задачи-на-свободное-падение/

Добавить комментарий Отменить ответ

Конспекты по физике:

7 класс

• Физические величины
• Строение вещества
• Механическое движение. Траектория
• Прямолинейное равномерное движение
• Неравномерное движение. Средняя скорость
• ЗАДАЧИ на движение с решением
• Масса тела. Плотность вещества
• ЗАДАЧИ на плотность, массу и объем
• Силы вокруг нас (силы тяжести, трения, упругости)
• ЗАДАЧИ на силу тяжести и вес тела
• Давление тел, жидкостей и газов
• ЗАДАЧИ на давление твердых тел с решениями
• ЗАДАЧИ на давление жидкостей с решениями
• Закон Архимеда
• Сообщающиеся сосуды. Шлюзы
• ЗАДАЧИ на силу Архимеда с решениями
• Механическая работа, мощность и КПД
• ЗАДАЧИ на механическую работу с решениями
• ЗАДАЧИ на механическую мощность
• Простые механизмы. Блоки
• Рычаг. Равновесие рычага. Момент силы
• ЗАДАЧИ на простые механизмы с решениями
• ЗАДАЧИ на КПД простых механизмов
• Механическая энергия. Закон сохранения энергии
• Физика 7: все формулы и определения
• ЗАДАЧИ на Сообщающиеся сосуды
• ЗАДАЧИ на силу упругости с решениями

8 класс

• Введение в оптику
• Тепловое движение. Броуновское движение
• Диффузия. Взаимодействие молекул
• Тепловое равновесие. Температура. Шкала Цельсия
• Внутренняя энергия
• Виды теплопередачи: теплопроводность, конвекция, излучение
• Количество теплоты. Удельная теплоёмкость
• Уравнение теплового баланса
• Испарение. Конденсация
• Кипение. Удельная теплота парообразования
• Влажность воздуха
• Плавление и кристаллизация
• Тепловые машины. ДВС. Удельная теплота сгорания топлива
• Электризация тел
• Два вида электрических зарядов. Взаимодействие зарядов
• Закон сохранения электрического заряда
• Электрическое поле. Проводники и диэлектрики
• Постоянный электрический ток
• Сила тока. Напряжение
• Электрическое сопротивление
• Закон Ома. Соединение проводников
• Работа и мощность электрического тока
• Закон Джоуля-Ленца и его применение
• Электромагнитные явления
• Колебательные и волновые явления
• Физика 8: все формулы и определения
• ЗАДАЧИ на количество теплоты с решениями
• ЗАДАЧИ на сгорание топлива с решениями
• ЗАДАЧИ на плавление и отвердевание
• ЗАДАЧИ на парообразование и конденсацию
• ЗАДАЧИ на КПД тепловых двигателей
• ЗАДАЧИ на Закон Ома с решениями
• ЗАДАЧИ на сопротивление проводников
• ЗАДАЧИ на Последовательное соединение
• ЗАДАЧИ на Параллельное соединение
• ЗАДАЧИ на Работу электрического тока
• ЗАДАЧИ на Мощность электрического тока
• ЗАДАЧИ на Закон Джоуля-Ленца
• Опыты Эрстеда. Магнитное поле. Электромагнит
• Магнитное поле постоянного магнита
• Действие магнитного поля на проводник с током
• Электромагнитная индукция. Опыты Фарадея
• Явления распространения света
• Дисперсия света. Линза
• Оптические приборы
• Электромагнитные колебания и волны

9 класс

• Введение в квантовую физику
• Формула времени. Решение задач
• ЗАДАЧИ на Прямолинейное равномерное движение
• ЗАДАЧИ на Прямолинейное равноускоренное движение
• ЗАДАЧИ на Свободное падение с решениями
• ЗАДАЧИ на Законы Ньютона с решениями
• ЗАДАЧИ закон всемирного тяготения
• ЗАДАЧИ на Движение тела по окружности
• ЗАДАЧИ на искусственные спутники Земли
• ЗАДАЧИ на Закон сохранения импульса
• ЗАДАЧИ на Механические колебания
• ЗАДАЧИ на Механические волны
• ЗАДАЧИ на Состав атома и ядерные реакции
• ЗАДАЧИ на Электромагнитные волны
• Физика 9 класс. Все формулы и определения
• Относительность движения
• Равномерное прямолинейное движение
• Прямолинейное равноускоренное движение
• Свободное падение
• Скорость равномерного движения тела по окружности
• Масса. Плотность вещества
• Сила – векторная физическая величина
• Первый закон Ньютона
• Второй закон Ньютона. Третий закон Ньютона
• Трение покоя и трение скольжения
• Деформация тела
• Всемирное тяготение. Сила тяжести
• Импульс тела. Закон сохранения импульса
• Механическая работа. Механическая мощность
• Кинетическая и потенциальная энергия
• Механическая энергия
• Золотое правило механики
• Давление твёрдого тела. Давление газа
• Закон Паскаля. Гидравлический пресс
• Закон Архимеда. Условие плавания тел
• Механические колебания и волны. Звук
• МКТ. Агрегатные состояния вещества
• Радиоактивность. Излучения. Распад
• Опыты Резерфорда. Планетарная модель атома
• Состав атомного ядра. Изотопы
• Ядерные реакции. Ядерный реактор
• ЗАДАЧИ на Движение под действием нескольких сил
• ЗАДАЧИ на Движение под действием силы трения

10-11 классы

• Молекулярно-кинетическая теория
• Кинематика. Теория и формулы + Шпаргалка
• Динамика. Теория и формулы + Шпаргалка
• Законы сохранения. Работа и мощность. Теория, Формулы, Шпаргалка
• Статика и гидростатика. Теория и формулы + Шпаргалка
• Термодинамика. Теория, формулы, схемы
• Электростатика. Теория и формулы + Шпаргалка
• Постоянный ток. Теория, формулы, схемы
• Магнитное поле. Теория, формулы, схемы
• Электромагнитная индукция
• Закон сохранения импульса. Задачи ЕГЭ с решениями
• Колебания и волны Задачи ЕГЭ с решениями
• Физика 10 класс. Все формулы и темы
• Физика 11 класс. Все формулы и определения
• Световые кванты
• ЕГЭ Квантовая физика. Задачи с решениями
• Излучения и спектры
• Атомная физика (физика атома)
• ЕГЭ Закон Кулона. ЗАДАЧИ с решениями
• Электрическое поле. ЗАДАЧИ с решениями
• Потенциал. Разность потенциалов. ЗАДАЧИ с решениями
• Закон Ома. Соединение проводников. ЗАДАЧИ на ЕГЭ
• Закон Ома для всей цепи. ЗАДАЧИ на ЕГЭ
• ЗАДАЧИ на Колебания и волны (с решениями)
• Электромагнитные колебания

Найти конспект:

О проекте

Сайт «УчительPRO» — некоммерческий школьный проект учеников, их родителей и учителей. Продолжая использовать наш сайт, вы даете согласие на обработку файлов cookie и других пользовательских данных в целях функционирования сайта, проведения статистических исследований и обзоров. Если вы не хотите, чтобы ваши данные обрабатывались, покиньте сайт.

Возрастная категория: 12+

(с) 2021 Учитель.PRO — Копирование информации с сайта только при указании активной ссылки на сайт!

💡 Видео

УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать

Графики зависимости кинематических величин от времени при равномерном и равноускоренном движенииСкачать

Как разложить силы на проекции (динамика 10-11 класс) ЕГЭ по физикеСкачать

Уравнение движения тела дано в виде x=2−3t. ВычислиСкачать

Урок 9. Проекции вектора на координатные осиСкачать

Векторы и действия над ними, проекция вектора на координатные оси. 9 класс.Скачать

Графики зависимости пути и скорости от времениСкачать

Формула ускоренияСкачать

Задача из ЕГЭ по физике │Анализ графика #1Скачать