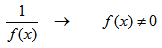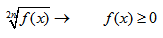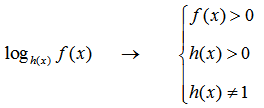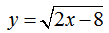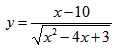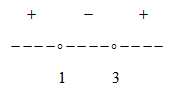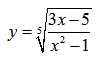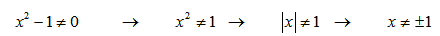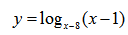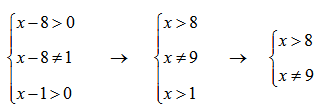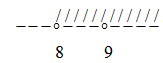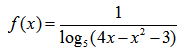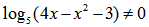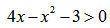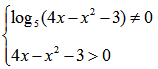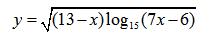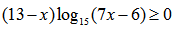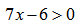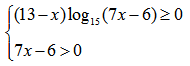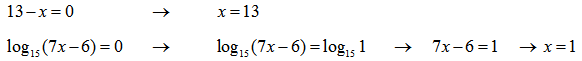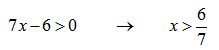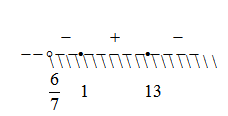- Что такое дробно-рациональные уравнения
- Как решаются дробно-рациональные уравнения
- Примеры задач с ответами для 9 класса
- Как найти область определения функции?
- Определение:
- Областью определения называется множество значений, которые может принимать x. Обозначение D(f).
- 1. Дробная функция — ограничение на знаменатель.
- 2. Корень четной степени — ограничение на подкоренное выражение.
- 3. Логарифмы — ограничение на основание логарифма и подлогарифмическое выражение.
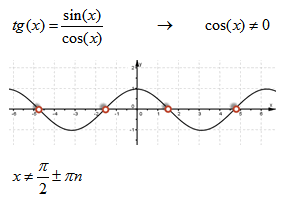
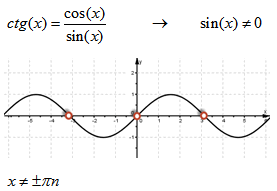
- 3. Тригонометрические tg(x) и ctg(x) — ограничение на аргумент.
- 4. Обратные тригонометрические функции.
- Пример нахождения области определения функции №1
- Нахождение области определения любой линейной функции, т.е. функции первой степени:
- Пример нахождения области определения функции №2
- Пример нахождения области определения функции №3
- Рассмотрим пример нахождения области определения функции с корнем четной степени:
- Пример нахождения области определения функции №4
- Рассмотрим пример нахождения области определения функции с корнем четной степени в знаменателе:
- Пример нахождения области определения функции №5
- Рассмотрим пример нахождения области определения функции с корнем нечетной степени:
- Пример нахождения области определения функции №6
- Пример нахождения области определения функции №7
- Пример нахождения области определения функции №8
- Как найти область определения функции
- Что такое область определения функции?
- Общий принцип на самых простых примерах
- Область определения корня n-й степени
- Область определения степенной функции
- Область определения степенной функции с дробным показателем степени
- Область определения показательной и логарифмической функции
- Область определения показательной функции
- Область определения логарифмической функции
- Найти область определения функции самостоятельно, а затем посмотреть решение
- Область определения тригонометрических функций
- Область определения обратных тригонометрических функций
- Область определения дроби
- Найти область определения функции самостоятельно, а затем посмотреть решение
- Область определения постоянной
- Область определения линейной функции
Видео:Функция. Область определения функции. Практическая часть. 10 класс.Скачать

Что такое дробно-рациональные уравнения
Дробно-рациональными уравнениями называют такие выражения, которые представляется возможным записать, как:
при P ( x ) и Q ( x ) в виде выражений, содержащих переменную.
Таким образом, дробно-рациональные уравнения обязательно содержат как минимум одну дробь с переменной в знаменателе с любым модулем.
9 x 2 — 1 3 x = 0
1 2 x + x x + 1 = 1 2
6 x + 1 = x 2 — 5 x x + 1
Уравнения, которые не являются дробно-рациональными:
Видео:§39.1 Нахождение области определения алгебраического выраженияСкачать

Как решаются дробно-рациональные уравнения
В процессе решения дробно-рациональных уравнений обязательным действием является определение области допустимых значений. Найденные корни следует проверить на допустимость, чтобы исключить посторонние решения.
Алгоритм действий при стандартном способе решения:
- Выписать и определить ОДЗ.
- Найти общий знаменатель для дробей.
- Умножить каждый из членов выражения на полученный общий параметр (знаменатель), сократить дроби, которые получились в результате, чтобы исключить знаменатели.
- Записать уравнение со скобками.
- Раскрыть скобки для приведения подобных слагаемых.
- Найти корни полученного уравнения.
- Выполним проверку корней в соответствии с ОДЗ.
- Записать ответ.
Пример 1
Разберем предложенный алгоритм на практическом примере. Предположим, что имеется дробно-рациональное уравнение, которое требуется решить:
x x — 2 — 7 x + 2 = 8 x 2 — 4
Начать следует с области допустимых значений:
x 2 — 4 ≠ 0 ⇔ x ≠ ± 2
Воспользуемся правилом сокращенного умножения:
x 2 — 4 = ( x — 2 ) ( x + 2 )
В результате общим знаменателем дробей является:
Выполним умножение каждого из членов выражения на общий знаменатель:
x x — 2 — 7 x + 2 = 8 x 2 — 4
x ( x — 2 ) ( x + 2 ) x — 2 — 7 ( x — 2 ) ( x + 2 ) x + 2 = 8 ( x — 2 ) ( x + 2 ) ( x — 2 ) ( x + 2 )
После сокращения избавимся от скобок и приведем подобные слагаемые:
x ( x + 2 ) — 7 ( x — 2 ) = 8
x 2 + 2 x — 7 x + 14 = 8
Осталось решить квадратное уравнение:
Согласно ОДЗ, первый корень является лишним, так как не удовлетворяет условию, по которому корень не равен 2. Тогда в ответе можно записать:
Видео:Дробно-рациональные уравнения. 8 класс.Скачать

Примеры задач с ответами для 9 класса
Требуется решить дробно-рациональное уравнение:
x x + 2 + x + 1 x + 5 — 7 — x x 2 + 7 x + 10 = 0
x x + 2 + x + 1 x + 5 — 7 — x x 2 + 7 x + 10 = 0
Определим область допустимых значений:
О Д З : x + 2 ≠ 0 ⇔ x ≠ — 2
x 2 + 7 x + 10 ≠ 0
D = 49 — 4 · 10 = 9
x 1 ≠ — 7 + 3 2 = — 2
x 2 ≠ — 7 — 3 2 = — 5
Квадратный трехчлен x 2 + 7 x + 10 следует разложить на множители, руководствуясь формулой:
a x 2 + b x + c = a ( x — x 1 ) ( x — x 2 )
x x + 2 + x + 1 x + 5 — 7 — x ( x + 2 ) ( x + 5 ) = 0
Заметим, что общим знаменателем для дробей является: ( x + 2 ) ( x + 5 ) . Умножим на этот знаменатель уравнение:
x x + 2 + x + 1 x + 5 — 7 — x ( x + 2 ) ( x + 5 ) = 0
Сократим дроби, избавимся от скобок, приведем подобные слагаемые:
x ( x + 2 ) ( x + 5 ) x + 2 + ( x + 1 ) ( x + 2 ) ( x + 5 ) x + 5 —
— ( 7 — x ) ( x + 2 ) ( x + 5 ) ( x + 2 ) ( x + 5 ) = 0
x ( x + 5 ) + ( x + 1 ) ( x + 2 ) — 7 + x = 0
x 2 + 5 x + x 2 + 3 x + 2 — 7 + x = 0
2 x 2 + 9 x — 5 = 0
Потребуется решить квадратное уравнение:
2 x 2 + 9 x — 5 = 0
Первый корень не удовлетворяет условиям ОДЗ, поэтому в ответ нужно записать только второй корень.
Дано дробно-рациональное уравнение, корни которого требуется найти:
4 x — 2 — 3 x + 4 = 1
В первую очередь следует переместить все слагаемые влево и привести дроби к минимальному единому знаменателю:
4 ( x + 4 ) x — 2 — 3 ( x — 2 ) x + 4 — 1 ( x — 2 ) ( x + 4 ) = 0
4 ( x + 4 ) — 3 ( x — 2 ) — ( x — 2 ) ( x + 4 ) ( x — 2 ) ( x + 4 ) = 0
4 x + 16 — 3 x + 6 — ( x 2 + 4 x — 2 x — 8 ) ( x — 2 ) ( x + 4 ) = 0
x + 22 — x 2 — 4 x + 2 x + 8 ( x — 2 ) ( x + 4 ) = 0
Заметим, что получилось нулевое значение для дроби. Известно, что дробь может равняться нулю, если в числителе нуль, а знаменатель не равен нулю. На основании этого можно составить систему:
— x 2 — x + 30 ( x — 2 ) ( x + 4 ) = 0 ⇔ — x 2 — x + 30 = 0 ( x — 2 ) ( x + 4 ) ≠ 0
Следует определить такие значения для переменной, при которых в дроби знаменатель будет обращаться в нуль. Такие значения необходимо удалить из ОДЗ:
( x — 2 ) ( x + 4 ) ≠ 0
Далее можно определить значения для переменных, которые при подстановке в уравнение обращают числитель в нуль:
— x 2 — x + 30 = 0 _ _ _ · ( — 1 )
Получилось квадратное уравнение, которое можно решить:
Сравнив корни с условиями области допустимых значений, можно сделать вывод, что оба корня являются решениями данного уравнения.
Нужно решить дробно-рациональное уравнение:
x + 2 x 2 — 2 x — x x — 2 = 3 x
На первом шаге следует перенести все слагаемые в одну сторону и привести дроби к минимальному единому знаменателю:
x + 2 1 x ( x — 2 ) — x x x — 2 — 3 ( x — 2 ) x = 0
x + 2 — x 2 — 3 ( x — 2 ) x ( x — 2 ) = 0
x + 2 — x 2 — 3 x + 6 x ( x — 2 ) = 0
— x 2 — 2 x + 8 x ( x — 2 ) = 0 ⇔ — x 2 — 2 x + 8 = 0 x ( x — 2 ) ≠ 0
Перечисленные значения переменной обращают знаменатель в нуль. По этой причине их необходимо удалить из области допустимых значений.
— x 2 — 2 x + 8 = 0 _ _ _ · ( — 1 )
Корни квадратного уравнения:
x 1 = — 4 ; x 2 = 2
Заметим, что второй корень не соответствует ОДЗ. Таким образом, в ответе остается только первый корень.
Найти корни уравнения:
x 2 — x — 6 x — 3 = x + 2
Согласно стандартному алгоритму решения дробно-рациональных уравнений, выполним перенос всех слагаемых в одну сторону. Далее необходимо привести к дроби к наименьшему общему знаменателю:
x 2 — x — 6 1 x — 3 — x ( x — 3 ) — 2 ( x — 3 ) = 0
x 2 — x — 6 — x ( x — 3 ) — 2 ( x — 3 ) x — 3 = 0
x 2 — x — 6 — x 2 + 3 x — 2 x + 6 x — 3 = 0
0 x x — 3 = 0 ⇔ 0 x = 0 x — 3 ≠ 0
Такое значение переменной, при котором знаменатель становится равным нулю, нужно исключить из области допустимых значений:
Заметим, что это частный случай линейного уравнения, которое обладает бесконечным множеством корней. При подстановке какого-либо числа на место переменной х в любом случае числовое равенство будет справедливым. Единственным недопустимым значением для х в данном задании является число 3, которое не входит в ОДЗ.
Ответ: х — любое число, за исключением 3.
Требуется вычислить корни дробно-рационального уравнения:
5 x — 2 — 3 x + 2 = 20 x 2 — 4
На первом этапе необходимо выполнить перенос всех слагаемых влево, привести дроби к минимальному единому знаменателю:
5 ( x + 2 ) x — 2 — 3 ( x — 2 ) x + 2 — 20 1 ( x — 2 ) ( x + 2 ) = 0
5 ( x + 2 ) — 3 ( x — 2 ) — 20 ( x — 2 ) ( x + 2 ) = 0
5 x + 10 — 3 x + 6 — 20 ( x — 2 ) ( x + 2 ) = 0
2 x — 4 ( x — 2 ) ( x + 2 ) = 0 ⇔ 2 x — 4 = 0 ( x — 2 ) ( x + 2 ) ≠ 0
( x — 2 ) ( x + 2 ) ≠ 0
Данные значения переменной х являются недопустимыми, так как в этом случае теряется смысл дроби в связи с тем, что знаменатель принимает нулевое значение.
Заметим, что 2 не входит в область допустимых значений. В связи с этим, можно заключить, что у уравнения отсутствуют корни.
Ответ: корни отсутствуют
Нужно найти корни уравнения:
x — 3 x — 5 + 1 x = x + 5 x ( x — 5 )
Начнем с определения ОДЗ:
— 5 ≠ 0 x ≠ 0 x ( x — 5 ) ≠ 0 x ≠ 5 x ≠ 0
При умножении обеих частей уравнения на единый знаменатель всех дробей и сокращении аналогичных выражений, которые записаны в числителе и знаменателе, получим:
x — 3 x — 5 + 1 x = x + 5 x ( x — 5 ) · x ( x — 5 )
( x — 3 ) x ( x — 5 ) x — 5 + x ( x — 5 ) x = ( x + 5 ) x ( x — 5 ) x ( x — 5 )
( x — 3 ) x + x = x + 5
Прибегая к арифметическим преобразованиям, можно записать уравнение в упрощенной форме:
x 2 — 3 x + x — 5 = x + 5 → x 2 — 2 x — 5 — x — 5 = 0 → x 2 — 3 x — 10 = 0
Для дальнейших действий следует определить, к какому виду относится полученное уравнение. В нашем случае уравнение является квадратным с коэффициентом при x 2 , который равен 1. Таким образом, целесообразно воспользоваться теоремой Виета:
x 1 · x 2 = — 10 x 1 + x 2 = 3
В этом случае подходящими являются числа: -2 и 5.
Второе значение не соответствует области допустимых значений.
Видео:Как найти область определения функции? #shortsСкачать

Как найти область определения функции?
 |
 | на графике тангенса | 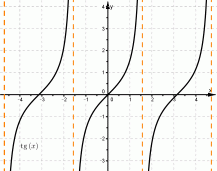 |
Для котангенса:
 | на графике котангенса | 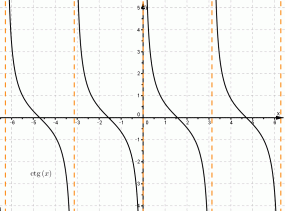 |
4. Обратные тригонометрические функции.
| Арксинус | Арккосинус | Арктангенс, Арккотангенс |
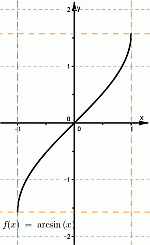 | 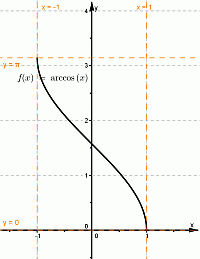 | 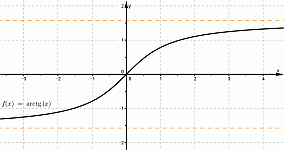 |
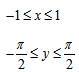
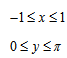
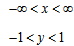
| Пример 1 | Пример 2 |
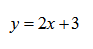 | 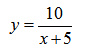 |
| Пример 3 | Пример 4 |
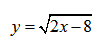 | 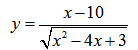 |
| Пример 5 | Пример 6 |
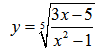 | 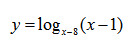 |
| Пример 7 | Пример 8 |
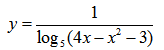 | 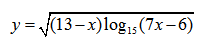 |
| Пример 9 | Пример 10 |
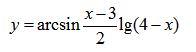 | 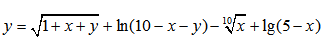 |
| Пример 11 | Пример 12 |
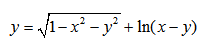 | 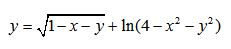 |
| Пример 13 | Пример 14 |
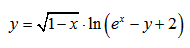 |
| Пример 15 | Пример 16 |
Пример нахождения области определения функции №1
Видео:Как решать дробно-рациональные уравнения? | МатематикаСкачать

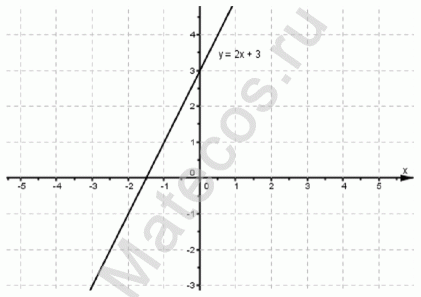
Нахождение области определения любой линейной функции, т.е. функции первой степени:
y = 2x + 3 — уравнение задает прямую на плоскости.
Посмотрим внимательно на функцию и подумаем, какие же числовые значения мы сможем подставить в уравнение вместо переменной х?
Попробуем подставить значение х=0
Так как y = 2·0 + 3 = 3 — получили числовое значение, следовательно функция существует при взятом значении переменной х=0.
Попробуем подставить значение х=10
так как y = 2·10 + 3 = 23 — функция существует при взятом значении переменной х=10 .
Попробуем подставить значение х=-10
так как y = 2·(-10) + 3 = -17 — функция существует при взятом значении переменной х=-10 .
Уравнение задает прямую линию на плоcкости, а прямая не имеет ни начала ни конца, следовательно она существует для любых значений х.
Заметим, что какие бы числовые значения мы не подставляли в заданную функцию вместо х, всегда получим числовое значение переменной y.
Следовательно, функция существует для любого значения x ∈ R или запишем так: D(f) = R
Формы записи ответа: D(f)=R или D(f)=(-∞:+∞)или x∈R или x∈(-∞:+∞)
Для любой функции вида y = ax + b областью определения является множество действительных чисел.
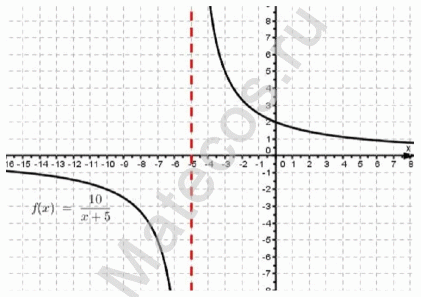
Пример нахождения области определения функции №2
Задана функция вида:
y = 10/(x + 5) — уравнение гиперболы
Имея дело с дробной функцией, вспомним, что на ноль делить нельзя. Следовательно функция будет существовать для всех значений х, которые не
обращают знаменатель в ноль. Попробуем подставить какие-либо произвольные значения х.
При х = 0 имеем y = 10/(0 + 5) = 2 — функция существует.
При х = 10 имеем y = 10/(10 + 5) = 10/15 = 2/ 3 — функция существует.
При х = -5 имеем y = 10/(-5 + 5) = 10/0 — функция в этой точке не существует.
Т.е. если заданная функция дробная, то необходимо знаменатель приравнять нулю и найти такую точку, в которой функция не существует.
x + 5 = 0 → x = -5 — в этой точке заданная функция не существует.
Для наглядности изобразим графически:
На графике также видим, что гипербола максимально близко приближается к прямой х = -5 , но самого значения -5 не достигает.
Видим, что заданная функция существует во всех точках действительной оси, кроме точки x = -5
Формы записи ответа: D(f)=R или D(f)=(-∞;-5) ∪ (-5;+∞) или x ∈ R или x ∈ (-∞;-5) ∪ (-5;+∞)
Если заданная функция дробная, то наличие знаменателя накладывает условие неравенства нулю знаменателя.
Пример нахождения области определения функции №3
Видео:Область ОПРЕДЕЛЕНИЯ рациональной ДРОБИ! Самое простое объяснение !Скачать

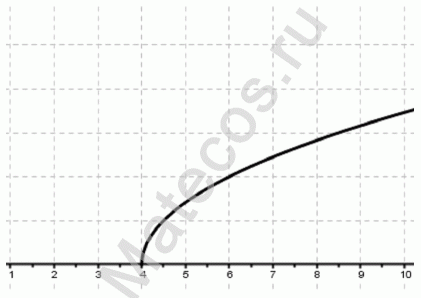
Рассмотрим пример нахождения области определения функции с корнем четной степени:
Так как квадратный корень мы можем извлечь только из неотрицательного числа, следовательно, функция под корнем — неотрицательна.
Решим простое неравенство:
2х — 8 ≥ 0 → 2х ≥ 8 → х ≥ 4
Заданная функция существует только при найденных значениях х ≥ 4 или D(f)=[4 ;+∞) или x ∈ [4 ;+∞) .
На графике видим, что функция существует для найденных значений х : х ≥ 4 или D(f)=[4 ;+∞) или x ∈ [4 ;+∞) .
При попытке подставить вместо х значения, отличные от найденных, под корнем получим отрицательное число, те в этих точках функция не существует.
Если заданная функция содержит квадратный корень (или корень любой четной степени), то обязательно накладывается условие неотрицательности (≥0) на подкоренное выражение. Если квадратный корень находится в знаменателе функции, у которой мы находим область определения, то на подкоренное выражение накладывается условие положительности (>0), так как знаменатель всегда должен быть отличен от нуля.
Пример нахождения области определения функции №4
Видео:Область определения (корня) функции #2. Алгебра 10 класс.Скачать

Рассмотрим пример нахождения области определения функции с корнем четной степени в знаменателе:
В числителе имеем линейную функцию, область определения которой множество всех действительных чисел. (см. пример 1)
В знаменателе — квадратный корень, накладывает условие на подкоренное выражение, не забывая о том, что знаменатель всегда отличен от нуля.
x 2 — 4x + 3 > 0 → (x — 1)(x — 3) > 0
Решим строгое неравенство методом интервалов:
Видим, что функция положительна на следующих интервалах: x∈(-∞;1)∪(3;+∞)
Нашли такие значения переменной х, при которых функция существует — нашли ОДЗ функции.
Пример нахождения области определения функции №5
Видео:Функция. Область определения и область значений функцииСкачать
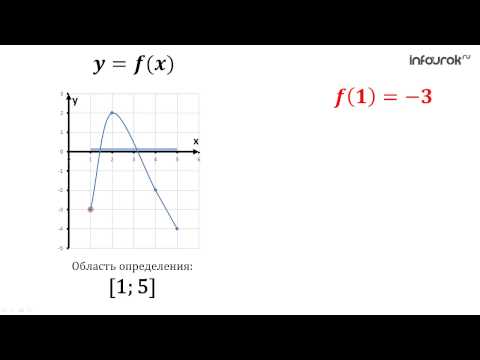
Рассмотрим пример нахождения области определения функции с корнем нечетной степени:
Имеем дело с корнем нечетной степени. Так как корень нечетной степени существует при любых значениях подкоренного выражения, то заданная дробная функция под корнем может принимать любые значения.
В числителе дробной функции — уравнение первой сnепени, которое существует при любых значениях переменной. Знаменатель любой дроби отличен от нуля. Следовательно, при нахождении ОДЗ заданного выражения имеем дело лишь с одним ограничением — ограничение на знаменатель дроби.
Пример нахождения области определения функции №6
Рассмотрим пример нахождения области определения логарифма:
Простенький пример на область определения логарифмической функции.
Помним, что основание логарифма положительно и отлично от нуля. Подлогарифмическое выражение положительно:
Покажем на числовой прямой:
Получили ОДЗ: x∈(8;9)∪(9;+∞)
Пример нахождения области определения функции №7
Задана функция вида:
1 ограничение основывается на наложении ограничения на знаменатель дроби (отличен от нуля):
Второе ограничение — подлогарифмическое выражение положительно:
Т.е. для определения области определения заданной функции необходимо решить систему:
Необходимо решить каждое из ограничений системы по отдельности и пересечь получившиеся результаты.
Допускаю, что читатель самостоятельно может это проделать и перехожу к разбору следующего примера.
Пример нахождения области определения функции №8
Рассмотрим следующий пример:
Имеем дело с корнем четной степени, следовательно первое ограничение на подкоренное выражение:
Имеем дело с логарифмом, следовательно ограничение на подлогарифмическую функцию:
Таким образом для определения области определения исходной функции необходимо решить систему неравенств:
Каждое из неравенств решим по отдельности.
Первое неравенство будем решать методом интервалов: найдем корни каждого из выражений неравенства, вынесем их на координатную плоскость и расставим знаки неравенства в каждом из полученных интервалов.
Выносим на координатную прямую:
Объясню как расставлены знаки в каждом из интервалов:
Значения левее 6/7 нет смысла рассматривать, так как логарифм для этих значений не существует.
1-ый интервал: (6/7;1]
Основание логарифма больше единицы, следовательно функция возрастающая. В корне x=1 логарифм меняет свое значение с » — » на » + «.
Видео:Область определения (дроби) функции #1. Алгебра 10 класс.Скачать

Как найти область определения функции
Видео:Область определения функцийСкачать

Что такое область определения функции?
Начнём с краткого определения. Область определения функции y=f(x) — это множество значений X, для которых существуют значения Y.
Войдём в тему более основательно. Каждой точке графика функции соответствуют:
- определённое значение «икса» — аргумента функции;
- определённое значение «игрека» — самой функции.
Верны следующие факты.
- От аргумента — «икса» — вычисляется «игрек» — значения функции.
- Область определения функции — это множества всех значений «икса», для которых существует, то есть может быть вычислен «игрек» — значение функции. Иначе говоря, множество значений аргумента, на котором «функция работает».
Можно понимать область определения функции и как проекцию графика функции на ось Ox.
Что требуется, чтобы уверенно находить область определения функции? Во-первых, нужно различать виды функций (корень, дробь, синус и др.). Во-вторых, решать уравнения и неравенства с учетом вида функции (например, на что нельзя делить, какое выражение не может быть под знаком корня и тому подобное). Согласитесь, не так уж много и не так сложно. При изучении темы области определения функции поможет материал Свойства и графики элементарных функций. А поскольку областью определения функции служат различные множества, а также их объединения и пересечения, то пригодится и материал Множества и операции над множествами.
Итак, чтобы находить области определения распространённых функций, порешаем уравнения и неравенства с одной переменной.
После этого экскурса в важную составную матанализа многие согласятся, что найти область определения функции не очень сложно.
Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы. Приступаем к практике.
Видео:Алгебра 9 класс. Область определения функцииСкачать

Общий принцип на самых простых примерах
Пример 1. На рисунке изображён график функции 
и решая это уравнение:
получаем значение, не входящее в область определения функции: 1. То есть, область определения заданной функции — это все значения «икса» от минус бесконечности до единицы и от единицы до плюс бесконечности. Это хорошо видно на графике. Приведённый здесь пример функции относится к виду дробей. На уроке разберём решения всех распространённых видов функций.
Пример 2. Как найти область определения функции игрек равен квадратному корню из икса минус пять (подкоренное выражение икс минус пять) (
Если перенести какое-либо слагаемое в другую часть неравенства с противоположным знаком, то мы получим равносильное неравенство с тем же знаком неравенства. Переносим минус 5 и получаем неравенство
Получаем решение: область определения функции — все значения икса больше или равно пяти (или икс принадлежит промежутку от пяти включительно до плюс бесконечности).
На чертеже сверху — фрагмент числовой оси. На ней область опредения рассмотренной функции заштрихована, при этом в «плюсовом» направлении штриховка продолжается бесконечно вместе с самой осью.
Видео:Алгебра 8. Урок 1 - Рациональное выражение и его ОДЗСкачать

Область определения корня n-й степени
В случае, функции корня n-й степени, то есть когда функция задана формулой 
если n — чётное число, то областью определения функции является множество всех неотрицательных действительных чисел, то есть [0; + ∞[ ;
если n — нечётное число, то областью определения функции является множество всех действительных чисел, то есть ]- ∞; + ∞[ .
Пример 3. Найти область определения функции 
Решение. Как следует из определения, корень чётной степени имеет смысл, если подкоренное выражение неотрицательно. Поэтому решаем неравенство

Это квадратное неравенство

По формуле 

По формуле 

Найденные точки разбивают числовую прямую на три промежутка:


При этом знак квадратного трёхчлена (больше или меньше нуля) совпадает со знаком коэффициента a во всех точках промежутков

и противоположен знаку коэффициента a во всех точках промежутка 
В нашем случае имеем отрицательный коэффициент a=-1 , поэтому квадратный трёхчлен неотрицателен во всех точках промежутка 
Следовательно, область определения данной функции — [- 1; 1] .
Заштрихованная область числовой прямой на чертеже сверху — это область определения данной функции.
Видео:№354 Найти область определения логарифмической функции (АНА 10-11 кл., Алимов Ш.А.)Скачать

Область определения степенной функции
Область определения степенной функции находится в зависимости от вида степени в выражении.
Область определения степенной функции с дробным показателем степени
В случае, когда функция задана формулой 
если 
если 
Пример 4. Найти область определения функции 
Решение. Выражение функции можно представить так:
Квадратный трёхчлен в скобках в знаменателе должен быть строго больше нуля (ещё и потому, что дробный показатель степени данной степенной функции — отрицательный). Поэтому решим строгое неравенство, когда квадратный трёхчлен в скобках строго больше нуля:


Дикриминант получился отрицательный. Следовательно сопряжённое неравенству квадратное уравнение не имеет корней. А это значит, что квадратный трёхчлен ни при каких значениях «икса» не равен нулю. Таким образом, область определения данной функции — вся числовая ось, или, что то же самое — множество R действительных чисел, или, что то же самое — ]- ∞; + ∞[ .
Пример 5. Найти область определения функции 
Решение. Оба слагаемых в выражении функции — степенные функции с положительными дробными показателями степеней. Следовательно, область определения данной функции — множество [0; + ∞[ .
На чертеже сверху заштрихована часть числовой прямой от нуля (включительно) и больше, причём штриховка продолжается вместе с самой прямой до плюс бесконечности.
Область определения степенной функции с целым показателем степени
В случае, когда функция задана формулой 
если a — положительное, то областью определения функции является множество всех действительных чисел, то есть ]- ∞; + ∞[ ;
если a — отрицательное, то областью определения функции является множество ]- ∞; 0[ ∪ ]0 ;+ ∞[ , то есть вся числовая прямая за исключением нуля.
На соответствующем чертеже сверху вся числовая прямая заштрихована, а точка, соответствующая нулю, выколота (она не входит в область определения функции).
Пример 6. Найти область определения функции 
Решение. Первое слагаемое целой степенью икса, равной 3, а степень икса во втором слагаемом можно представить в виде единицы — так же целого числа. Следовательно, область определения данной функции — вся числовая прямая, то есть ]- ∞; + ∞[ .
Видео:Функция. Множество значений функции. Практическая часть. 10 класс.Скачать
Область определения показательной и логарифмической функции
Область определения показательной функции
В случае, когда функция задана формулой 
Область определения логарифмической функции
Логарифмическая функция 
Найти область определения функции самостоятельно, а затем посмотреть решение
Пример 7. Найти область определения функции 
Пример 8. Найти область определения функции 
Видео:Область определения тригонометрических функцийСкачать

Область определения тригонометрических функций
Область определения функции y = cos(x) — так же множество R действительных чисел.
Область определения функции y = tg(x) — множество R действительных чисел, кроме чисел 
Область определения функции y = ctg(x) — множество R действительных чисел, кроме чисел 
Пример 9. Найти область определения функции 
Решение. Внешняя функция — десятичный логарифм и на область её определения распространяются условия области определения логарифмической функции вообще. То есть, её аргумент должен быть положительным. Аргумент здесь — синус «икса». Пользуясь тригонометической таблицей (или поворачивая воображаемый циркуль по окружности), видим, что условие sin x > 0 нарушается при «иксе» равным нулю, «пи», два, умноженном на «пи» и вообще равным произведению числа «пи» и любого чётного ( 2kπ ) или нечётного целого числа ( (2k+1)π ).
Таким образом, область определения данной функции задаётся выражением

где k — целое число.
Область определения обратных тригонометрических функций
Область определения функции y = arcsin(x) — множество [-1; 1] .
Область определения функции y = arccos(x) — так же множество [-1; 1] .
Область определения функции y = arctg(x) — множество R действительных чисел.
Область определения функции y = arcctg(x) — так же множество R действительных чисел.
Пример 10. Найти область определения функции 
Решение. Решим неравенство:
Решение получили, основываясь на свойстве неравенств: если все части верного неравенства умножить на одно и то же положительное число, то получится также верное неравество. В данном случае умножали на 4.
Таким образом, получаем область определения данной функции — отрезок [- 4; 4] .
Пример 11. Найти область определения функции 
Решение. Решим два неравенства:
Решение первого неравенства:
Решение получили, основываясь на свойстве неравенств: если обе части верного неравенства умножить на одно и то же отрицательное число изменить знак неравенства на противоположный, то получится верное неравенство. В данном случае умножали на минус 2.
Аналогично и решение второго неравенства:
Таким образом, получаем область определения данной функции — отрезок [0; 1] .
Видео:Область определения логарифмических функций (примеры)Скачать

Область определения дроби
Если функция задана дробным выражением, в котором переменная находится в знаменателе дроби, то областью определения функции является множество R действительных чисел, кроме таких x , при которых знаменатель дроби обращается в нуль.
Пример 12. Найти область определения функции 
Решение. Решая равенство нулю знаменателя дроби:
находим область определения данной функции — множество ]- ∞; — 2[ ∪ ]- 2 ;+ ∞[ , то есть все числа, кроме минус 2.
Пример 13. Найти область определения функции 
Решение. Решим уравнение:
Таким образом, получаем область определения данной функции — ]- ∞; — 1[ ∪ ]- 1 ; 1[ ∪ ]1 ;+ ∞[ , то есть все числа, кроме минус единицы и единицы.
Пример 14. Найти область определения функции 
Решение. Область определения первого слагаемого — данной функции — множество R действительных чисел, второго слагаемого — все действительные числа, кроме -2 и 2 (получили, решая равенство нулю знаменателя, как в предыдущем примере). В этом случае область определения функции должна удовлетворять условиями определения обоих слагаемых. Следовательно, область определения данной функции — ]- ∞; — 2[ ∪ ]- 2 ; 2[ ∪ ]2 ;+ ∞[ , то есть все числа, кроме -2 и 2.
Пример 15. Найти область определения функции 
Решение. Решим уравнение:
Уравнение не имеет действительных корней. Но функция определена только на действительных числах. Таким образом, получаем область определения данной функции — вся числовая прямая или, что то же самое — множество R действительных чисел или, что то же самое — ]- ∞; + ∞[ .
То есть, какое бы число мы не подставляли вместо «икса», знаменатель никогда не будет равен нулю.
Пример 16. Найти область определения функции 
Решение. Решим уравнение:
Таким образом, получаем область определения данной функции — ]- ∞; — 1[ ∪ ]- 1 ; 0[ ∪ ]0 ; 1[ ∪ ]1 ;+ ∞[ .
Пример 17. Найти область определения функции 
Решение. Кроме того, что знаменатель не может быть равным нулю, ещё и выражение под корнем не может быть отрицательным. Сначала решим уравнение:
График квадратичной функции под корнем представляет собой параболу, ветви которой направлены вверх. Как следует из решения квадратного уравнения, парабола пересекает ось Ox в точках 1 и 2. Между этими точками линия параболы находится ниже оси Ox, следовательно значения квадратичной функции между этими точками отрицательное. Таким образом, исходная функция не определена на отрезке [1; 2] .
Найти область определения функции самостоятельно, а затем посмотреть решение
Пример 18. Найти область определения функции 
Пример 19. Найти область определения функции 
Видео:Функция. Область определения и область значения функции. Алгебра, 9 классСкачать

Область определения постоянной
Постоянная (константа) определена при любых действительных значениях x , следовательно, данная функция определена на всём множестве R действительных чисел. Это можно записать и так: областью определения данной функции является вся числовая прямая ]- ∞; + ∞[ .
Пример 20. Найти область определения функции y = 2 .
Решение. Область определения функции не указана, значит, в силу выше приведённого определения имеется в виду естественная область определения. Выражение f(x) = 2 определено при любых действительных значениях x , следовательно, данная функция определена на всём множестве R действительных чисел.
Поэтому на чертеже сверху числовая прямая заштрихована на всём протяжении от минус бесконечности до плюс бесконечности.
Видео:Как запомнить графики функцийСкачать

Область определения линейной функции
Если функция задана формулой вида y = kx + b , то область определения функции — множество R действительных чисел.