Химические реакции разделяются по признаку их молекулярности или по признаку порядка химической реакции.
Молекулярность химической реакции равна числу молекул (или других частиц), одновременным воздействием между которыми осуществляется элементарный акт химического превращения.
В зависимости от числа таких частиц различают моно (одно-) молекулярные, би (двух-) молекулярные и три (трех-) молекулярные реакции.
Мономолекулярные реакции — реакции разложения молекул:
Для нее закон Гульдберга — Вааге дает:
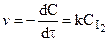
К бимолекулярным реакциям относятся взаимодействия двух одинаковых или различных молекул:
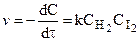
К тримолекулярным относятся реакции вида:
для которых справедливы соотношения:
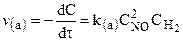
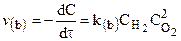
Молекулярность реакции — понятие теоретическое. Для того, чтобы знать молекулярность, нужно представлять, как именно протекает данная реакция, через взаимодействия каких молекул, через какие стадии.
В противоположность молекулярности порядок реакции — экспериментальная величина. Он связан с опытной зависимостью скорости данной реакции от концентрации исходных продуктов.
Порядок реакции равен сумме показателей степеней концентраций в уравнении, выражающем зависимость скорости реакции от концентрации и устанавливаемом экспериментально.
Для простых реакций, протекающих в полном соответствии с их стехиометрическим уравнением, порядок и молекулярность численно совпадают.
Причины несовпадения порядка реакции и ее молекулярности таковы.
А. Один из реагентов находится в большом избытке. Тогда в ходе реакции его концентрация изменяется незначительно и в уравнении закона Гульдберга — Вааге может быть принята постоянной.
В. Если данная реакция гетерогенная, то в зависимости от условий ее протекания порядок химической реакции изменяется.
С. Порядок каталитических реакций также может отличаться от молекулярности. Причина — сложный механизм таких реакций, не отражаемый стехиометрическим уравнением.
D. Наконец, для сложной реакции, протекающей в несколько стадий, характерно то, что основное влияние на скорость реакции может оказать какая-либо промежуточная стадия, которая и определит, в конечном итоге, порядок всей реакции.
Например, порядок реакции разложения пентаоксида азота
казалось бы, должен быть равен двум.
Исследования показали, что реакция протекает в несколько стадий (результаты анализа химического состава газовой фазы):
причем стадия (1) является наиболее медленной, а поэтому и определяющей скорость всего процесса. Поэтому и суммарная реакция — бимолекулярная реакция первого порядка.
По признаку “порядок химической реакции” различают реакции нулевого, первого, второго и третьего порядков.
Если реакция протекает по нулевому порядку, то

-dC = kd
и после интегрирования в интервале от С0 до С за время от 0 до 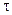
С — С0 = -k 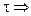
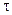
Следовательно, в реакциях нулевого порядка концентрация линейно уменьшается со временем. Уравнение (10.6) — кинетическое уравнение реакции нулевого порядка.
Период полураспада (полупревращения) 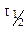
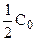
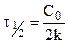
Константа скорости может быть найдена из (10.6):
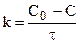
Выражение для скорости реакции первого порядка:
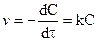
После разделения переменных и интегрирования от 0 до 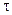
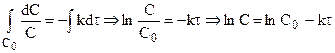
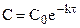
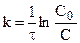
Подставляя 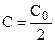
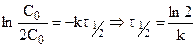
Таким образом, для реакции первого порядка выполняются следующие закономерности: зависимость концентрации от времени экспоненциальная; зависимость логарифма концентрации от времени линейная; период полураспада не зависит от начальной концентрации.
При равенстве концентраций исходных продуктов реакции кинетические уравнения реакций второго и третьего порядков соответственно запишутся:

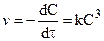
После разделения переменных:
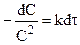
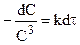
и после интегрирования:

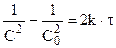
Из (10.13) для реакции второго порядка:
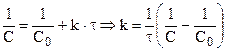
Полагая, что 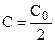
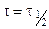

Для реакции третьего порядка:
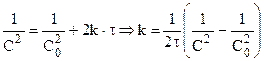
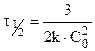
Таким образом для реакций второго порядка наблюдается линейная зависимость 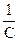
При интегрировании кинетических уравнений удобно обозначать концентрации реагентов с помощью изменения концентрации x одного из них в момент времени 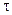
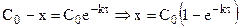
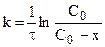
Эти уравнения можно получить, составив кинетическое уравнение вида:
и проинтегрировав его в интервале от 0 до 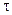
Для реакции второго порядка кинетическое уравнение выглядит:
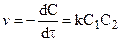
если 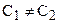
Тогда с учетом 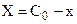
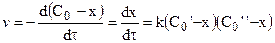
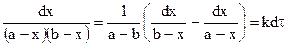
Далее после интегрирования:
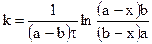
Для реакции третьего порядка, ограничиваясь случаем. когда две начальные концентрации одинаковы и равны а (С0’ = C0’’ = a), а третья начальная равна b (С0’’’ = b), уравнение для расчета константы скорости примет вид:
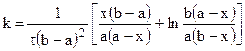
Дата добавления: 2015-05-21 ; просмотров: 16577 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Химические уравнения // Как Составлять Уравнения Реакций // Химия 9 классСкачать

Порядок и молекулярность реакции
Химическая кинетика (продолжение лекции)
Энергия активации зависит от природы реагирующих веществ и в некоторой степени от температуры.
Если энергия активации мала (меньше 40 кДж/моль), скорость реакции велика. Так, ионные реакции в растворах протекают практически мгновенно.
Если энергия активации реакции велика (больше 120 кДж/моль), скорость реакции мала. Например, синтез йодоводорода из I2 и H2 (Еа = 163 кДж/моль) при обычных условиях протекает за астрономический промежуток времени.
Реакции, энергия активации которых находится в пределах от 40 до 120 кДж/моль, протекают за время, которое можно зафиксировать в лабораторных условиях. Так, время протекания реакции разложения тиосульфата натрия серной кислотой, Еа = 86,5 кДж/моль:
составляет несколько минут.
Соотношение констант скоростей при разных температурах определяется уравнением:
 , , | (7) |
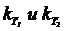
R – универсальная газовая постоянная, равная 8,31×10 — 3 кДж/моль×К;
Ea– энергия активации данной реакции в кДж/моль.
Данное уравнение позволяет рассчитать энергию активации системы.
Пример.
Для прямой элементарной реакции I2 + H2 = 2HI опытным путем определены константы скорости: при 443°С – 0,0067; при 508°С – 0,1059. Определить энергию активации данной реакции.
| T1 = 443 + 273 = 716 K | T2 = 508 + 273 = 781 K |
Вывод: скорость реакции очень мала, так как Еа> 120 кДж/моль.
Порядок и молекулярность реакции
Реакции, подчиняющиеся уравнениям типа:
принято классифицировать по признаку кинетического порядка.
Общим или суммарным порядком реакции называют сумму всех показателей степеней при концентрациях в выражении закона действующих масс, установленным опытным путем:
где a, b, с— частные порядки реакции, соответственно по веществам A, B и C.
Наиболее просты следующие случаи:
1) реакции нулевого порядка: 
2) реакции первого порядка: 
|

|



С общим кинетическим порядком выше третьего встречаться практически не приходится.
Для элементарных реакций (т. е. протекающих в один элементарный акт) показатели степеней a, b и c обычно представляют собой положительные целые числа. Для более сложных реакций известны дробные и даже отрицательные показатели.
Другой характеристикой механизма протекания химических реакций является молекулярность реакции.
Молекулярностью реакции называется число молекул, участвующих в одном элементарном акте реакции.
Следует отметить, что понятие молекулярности можно применять только для элементарных реакций. К числу элементарных реакций относится, например, разложение 1,2-диметилдиазена:

Данная реакция является мономолекулярной— в элементарном акте участвует одна молекула. Если в одном акте в реакцию вступают две молекулы, то реакция является бимолекулярной.Например:

Соответственно при тримолекулярной реакции в одном элементарном акте участвуют три частицы (молекулы):

Интересно, что большинство реакций, встречающихся на практике, кажутся простыми. Однако детальное изучение кинетики показывает, что зачастую они протекают по более сложным механизмам. Так, реакция термического разложения паров дихлорэтана:

на первый взгляд представляется элементарной.
Действительно, кинетическое уравнение этой реакции имеет вид:

что указывает на первый порядок.
Однако данная реакция не является мономолекулярной, так как протекает в несколько стадий:




В этом механизме первая и третья стадии мономолекулярны, а вторая и четвертая – бимолекулярны. Очевидно, говорить о молекулярности реакции разложения дихлорэтана в целом нельзя. В то же время можно говорить о ее первом кинетическом порядке.
Данный пример наглядно иллюстрирует факт, что порядок реакции далеко не всегда совпадает с ее молекулярностью. В целом, моно-, би- и тримолекулярные реакции являются, соответственно, реакциями первого, второго и третьего порядков; обратное же заключение может оказаться ошибочным.
Реакции I порядка
Для реакций I порядка убыль концентрации реагента определяется уравнением:
 | (8) |
где С – концентрация вещества в данный момент времени;
С0 – начальная концентрация вещества;
kI – константа скорости реакции первого порядка;
В логарифмической форме это выражение выглядит так:
 | (9) |
Из приведенных формул можно сделать ряд важных заключений:
1) константа скорости реакции первого порядка имеет размерность [время — 1 ] и может быть выражена в обратных секундах, минутах, часах и т. д.;
2) величина kI не зависит от способа выражения концентрации реагента;
3) в реакциях первого порядка одинаковым промежуткам времени отвечают одинаковые доли прореагировавшего вещества.
Последнее утверждение позволяет ввести понятие период полупревращения.
Периодом полупревращения (t1/2)называют время, необходимое для превращения половины первоначального количества вещества.
Таким образом, в момент времени t = t1/2 количество непрореагировавшего вещества составляет 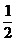
 . . | (10) |
Из данной формулы следует, что в реакциях первого порядка период полупревращения не зависит от начальной концентрации реагента.
В некоторых случаях удобно использовать формулу:
 , , | (11) |
которая позволяет определить время, за которое превращению подвергнется определенное количество исходного вещества.
В организме человека процессы метаболизма лекарственных препаратов протекают, в основном, в соответствии с уравнением реакции первого порядка. Период, за который превращению подвергается половина действующего начала препарата называется периодом полувыведения или полуэлиминации. Зная величины kI и t1/2, можно рассчитать оптимальные промежутки времени между приемами лекарственного средства.
Кинетические уравнения реакций различного порядка представлены в табл. 2.
Табл. 2. Кинетические уравнения реакций различного порядка.
| Порядок реакции | Кинетическое уравнение | Решение кинетического уравнения* | Период полупревращения |
 |  |  | |
 |  |  | |
 |  |  | |
 |  |  |
* при равных исходных концентрациях реагирующих веществ
Из приведенных уравнений следует, что для реакций различного порядка константы скорости имеют неодинаковые размерности. Действительно, константа скорости реакции второго порядка имеет размерность [л·моль — 1 ·время — 1 )], третьего порядка — [л 2 ·моль — 2 ·время — 1 ].
Таким образом, сравнивать значения констант скорости реакций различного порядка нельзя.
Видео:Химия | Молекулярные и ионные уравненияСкачать

Как определить молекулярность реакции по уравнению
Молекулярность реакции – это минимальное число молекул, участвующих в элементарном химическом процессе. По молекулярности элементарные химические реакции делятся на молекулярные (А →) и бимолекулярные (А + В →); тримолекулярные реакции встречаются чрезвычайно редко.
Если реакция протекает последовательно через несколько гомогенных или гетерогенных элементарных стадий, то суммарная скорость всего процесса определяется самой медленной его частью, а молекулярность заменяется порядком реакции – формальным показателем при концентрации реагирующих веществ. Поэтому весь процесс в целом лучше характеризует порядок реакции .
Кинетическое уравнение реакции только для элементарных стадий совпадает с выражением ЗДМ. В этих случаях молекулярность и порядок реакции совпадают, хотя и не всегда. Так, при избытке одного из компонентов элементарной реакции А + В (А >> В) скорость реакции будет практически зависеть от изменения концентрации вещества В (А = const), поэтому порядок бимолекулярной реакции понижается до первого. Аналогично тому, что скорость реакции может характеризоваться по любому веществу, участвующему в реакции, для реакции кинетические уравнения по веществу А и веществу В выглядят соответственно
 |
а общее кинетическое уравнение –
| (5.2) |
Здесь – общий порядок реакции. Запишем кинетическое уравнение в дифференциальной форме для разных исходных реагентов:
 |
Разделение переменных и интегрирование в пределах от нуля до τ дает приведенные в таб. 5.1 уравнения для реакций первого, второго и третьего порядков.
| ||||||||||||
| Таблица 5.1 Решения кинетических уравнений 2-го и 3-го порядка, приведенные в таблице 5.1, справедливы только при равных начальных концентрациях веществ В каждом случае кинетическое уравнение линейно в соответствующих координатах , что позволяет графически определить порядок реакции (рис. 5.2).
|
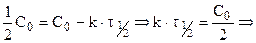




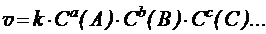









 1
1 в приповерхностном слое твердого углерода большой концентрационный градиент способствует практически мгновенному восполнению прореагировавшего кислорода. Следствием этого оказывается постоянство скорости реакции по кислороду, поскольку
в приповерхностном слое твердого углерода большой концентрационный градиент способствует практически мгновенному восполнению прореагировавшего кислорода. Следствием этого оказывается постоянство скорости реакции по кислороду, поскольку 
 скорость реакции будет соответствовать кинетическому уравнению первого порядка
скорость реакции будет соответствовать кинетическому уравнению первого порядка  При промежуточных давлениях кислорода порядок реакции изменяется в интервале от 0 до 1.
При промежуточных давлениях кислорода порядок реакции изменяется в интервале от 0 до 1.
















