Если материальная точка находится в движении, то ее координаты подвергаются изменениям. Этот процесс может происходить быстро или медленно.
Величина, которая характеризует быстроту изменения положения координаты, называется скоростью.
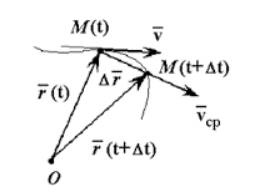
Средняя скорость – это векторная величина, численно равная перемещению в единицу времени, и сонаправленная с вектором перемещения » open=» υ = ∆ r ∆ t ; » open=» υ ↑ ↑ ∆ r .
Рисунок 1 . Средняя скорость сонаправлена перемещению
Модуль средней скорости по пути равняется » open=» υ = S ∆ t .
- Мгновенная скорость точки. Формулы
- Перемещение и мгновенная скорость
- Мгновенная скорость
- Скорость при неравномерном движении
- Мгновенная скорость
- Как рассчитать мгновенную скорость, формулу мгновенной скорости
- Рассмотрим уравнение скорости в терминах положения / смещения.
- Рассмотрим производную данного уравнения.
- Подставьте данное значение «t» в уравнение производной, чтобы найти мгновенную скорость.
- Как рассчитать Instantaneo скорость нас из графика
- Как рассчитать мгновенную скорость по графику положения-времени.
- Постройте график зависимости смещения от времени.
- Выберите любые две точки на графике st.
- Найдите наклон линии, соединяющей две точки, т. Е. Между точками A и B.
- Повторите несколько раз, чтобы найти уклон, перемещая B ближе к A.
- Вычислите наклон для бесконечно малого отрезка касательной.
- Формула мгновенной скорости
- Расчет формулы мгновенной скорости
- Формула средней и мгновенной скорости
- Формула мгновенной угловой скорости
- Формула мгновенной скорости и скорости
- Разница между мгновенной скоростью и мгновенной скоростью.
- Определение и формула мгновенной скорости
- Определение мгновенной скорости
- Формула мгновенной скорости
- Мгновенная скорость формула предела
- Как найти мгновенную скорость на графике
- Мгновенно s Интерпретация скорости из графика st
- Как найти мгновенную скорость из средней скорости
- Пример мгновенной скорости
- а). Определить мгновенную скорость частицы, движущейся по прямому пути за t = 2 секунды, с функцией положения «s», определенной как 4t² + 2t + 3?
- Проблема мгновенной скорости
- Некоторые проблемы с мгновенной скоростью,
- Проблема 1:
- Движение тележки задается функцией s = 3t 2 + 10t + 5. Вычислите его мгновенную скорость в момент времени t = 4 с.
- Проблема 2:
- Выстреленная пуля движется по прямой траектории, и ее уравнение движения имеет вид S (t) = 3t + 5t. 2 . Так, например, если он летит за 12 секунд до удара, найдите мгновенную скорость при t = 7 с.
- Проблема 3:
- Объект выпускается с определенной высоты, чтобы он мог свободно падать под действием силы тяжести. Уравнение движения для перемещения s (t) = 5.1 т. 2 . Какой будет мгновенная скорость объекта в момент времени t = 6 с после выпуска?
- Проблема 4:
- Найдите скорость при t = 2, учитывая уравнение перемещения s = 3t 3 — 3т 2 + 2т + 7.
- Проблема 5:
- Положение человека, движущегося по прямой, определяется выражением s (t) = 7t. 2 + 3t + 19, где t — время (секунды). Найдите уравнение для мгновенной скорости v (t) частицы в момент времени t.
- Проблема 6:
- Движение автомобиля описывается уравнением движения s = gt 2 + b, где b = 20 м и g = 12 м. Следовательно, найдите мгновенную скорость при t = 4 с.
- Проблема 7:
- Стол, упавший со здания 1145 футов, имеет высоту (в футах) над землей, определяемую как s (t) = 1145-12 т. 2 . Затем вычислите мгновенную скорость стола на 3 с?
- Проблема 8:
- Функция положения частиц определяется выражением s = (3t 2 )i — (4т)k + 2. какова его мгновенная скорость при t = 2? Каково его мгновенное ускорение как функция времени?
- Проблема 9:
- Положение насекомого определяется как s = 44 + 20t — 3t. 3 , где t в секундах, а s в метрах .
- а. Найдите среднюю скорость объекта между t = 0 и t = 4. s.
- б. В какое время между 0 и 4 мгновенная скорость равна нулю.
- Для расчета средней скорости
- Чтобы найти время, при котором мгновенная скорость равна нулю.
- Проблема 10:
- Частица движется с функцией смещения s = t 2 + 3 .
- Найдите положение при t = 2.
- Найдите среднюю скорость от t = 2 до t = 3.
- Найти его мгновенную скорость при t = 2 .
- Чтобы найти позицию при t = 2
- Для того, чтобы найти Средняя скорость.
- Чтобы найти мгновенную скорость
- Мгновенная скорость в зависимости от средней скорости
- Как найти мгновенная скорость без исчисления
- Как рассчитать мгновенную скорость и мгновенное ускорение
- 11 задачи:
- Пуля, выпущенная в космос, движется по прямой траектории, и ее уравнение движения имеет вид s (t) = 2t + 4t 2 . Если он движется в течение 12 секунд до удара, найдите мгновенную скорость и мгновенное ускорение в момент времени t = 3 секунды.
- Как найти мгновенную скорость и скорость
- 12 задачи:
- Почему можно рассчитать мгновенную скорость по кинематическим формулам только при постоянном ускорении
- Почему при вычислении мгновенной скорости мы берем небольшие промежутки времени. Как он дает скорость в этот момент, если мы рассчитываем ее за определенный промежуток времени?
- Различаются ли скорость и мгновенная скорость?
- Что такое мгновенная скорость на реальных примерах
- Часто задаваемые вопросы | FAQs
- Является ли мгновенная скорость вектором
- Как найти мгновенную скорость только с графиком положения и времени и без заданного уравнения
- Можно ли мгновенно изменить скорость
- Как я могу рассчитать смещение, если ускорение является функцией мгновенной скорости Задана начальная скорость
- От происхождения
- Из формулы
- Что такое средний и мгновенная скорость
- Мгновенное ускорение перпендикулярно мгновенной скорости
Видео:Мгновенная скорость. Сложение скоростей | Физика 10 класс #4 | ИнфоурокСкачать

Мгновенная скорость точки. Формулы
Мгновенная скорость характеризует движение в определенный момент времени. Выражение «скорость тела в данный момент времени» считается не корректным, но применимым при математических расчетах.
Мгновенной скоростью называют предел, к которому стремится средняя скорость » open=» υ при стремлении промежутка времени ∆ t к 0 :
υ = l i m ∆ t ∆ r ∆ t = d r d t = r ˙ .
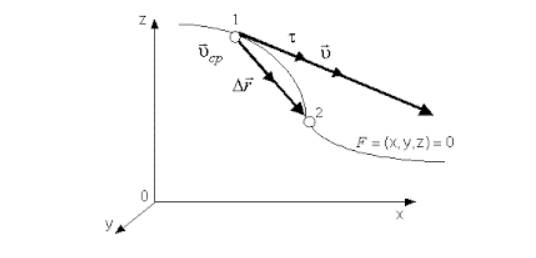
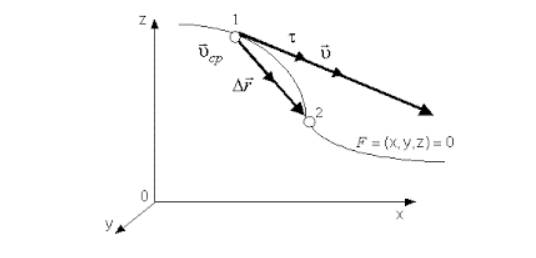
Направление вектора υ идет по касательной к криволинейной траектории, потому как бесконечно малое перемещение d r совпадает с бесконечно малым элементом траектории d s .
Рисунок 2 . Вектор мгновенной скорости υ
Имеющееся выражение υ = l i m ∆ t ∆ r ∆ t = d r d t = r ˙ в декартовых координатах идентично ниже предложенным уравнениям:
υ x = d x d t = x ˙ υ y = d y d t = y ˙ υ z = d z d t = z ˙ .
Видео:Мгновенная скорость (видео 6)| Векторы. Прямолинейное движение | ФизикаСкачать

Перемещение и мгновенная скорость
Запись модуля вектора υ примет вид:
υ = υ = υ x 2 + υ y 2 + υ z 2 = x 2 + y 2 + z 2 .
Чтобы перейти от декартовых прямоугольных координат к криволинейным, применяют правила дифференцирования сложных функций. Если радиус-вектор r является функцией криволинейных координат r = r q 1 , q 2 , q 3 , тогда значение скорости запишется как:
υ = d r d t = ∑ i = 1 3 ∂ r ∂ q i ∂ q i ∂ r = ∑ i = 1 3 ∂ r ∂ q i q ˙ i .
Рисунок 3 . Перемещение и мгновенная скорость в системах криволинейных координат
При сферических координатах предположим, что q 1 = r ; q 2 = φ ; q 3 = θ , то получим υ , представленную в такой форме:
υ = υ r e r + υ φ e φ + υ θ φ θ , где υ r = r ˙ ; υ φ = r φ ˙ sin θ ; υ θ = r θ ˙ ; r ˙ = d r d t ; φ ˙ = d φ d t ; θ ˙ = d θ d t ; υ = r 1 + φ 2 sin 2 θ + θ 2 .
Мгновенной скоростью называют значение производной от функции перемещения по времени в заданный момент, связанной с элементарным перемещением соотношением d r = υ ( t ) d t
Дан закон прямолинейного движения точки x ( t ) = 0 , 15 t 2 — 2 t + 8 . Определить ее мгновенную скорость через 10 секунд после начала движения.
Решение
Мгновенной скоростью принято называть первую производную радиус-вектора по времени. Тогда ее запись примет вид:
υ ( t ) = x ˙ ( t ) = 0 . 3 t — 2 ; υ ( 10 ) = 0 . 3 × 10 — 2 = 1 м / с .
Ответ: 1 м / с .
Движение материальной точки задается уравнением x = 4 t — 0 , 05 t 2 . Вычислить момент времени t о с т , когда точка прекратит движение, и ее среднюю путевую скорость » open=» υ .
Решение
Вычислим уравнение мгновенной скорости, подставим числовые выражения:
υ ( t ) = x ˙ ( t ) = 4 — 0 , 1 t .
4 — 0 , 1 t = 0 ; t о с т = 40 с ; υ 0 = υ ( 0 ) = 4 ; » open=» υ = ∆ υ ∆ t = 0 — 4 40 — 0 = 0 , 1 м / с .
Ответ: заданная точка остановится по прошествии 40 секунд; значение средней скорости равняется 0 , 1 м / с .
Видео:Рассмотрение темы: "Мгновенная скорость"Скачать

Мгновенная скорость

Средняя оценка: 4.3
Всего получено оценок: 225.
Средняя оценка: 4.3
Всего получено оценок: 225.
Большинство движений в природе являются неравномерными. При описании таких движений большое значение имеет параметр «мгновенная скорость». Рассмотрим его подробнее.
Видео:Физика - перемещение, скорость и ускорение. Графики движения.Скачать

Скорость при неравномерном движении
Скорость – величина, показывающая, какое расстояние проходит материальная точка за единицу времени:

Однако, для определения положения материальной точки в любой момент времени, во многих случаях эту формулу применять нельзя.
В самом деле, если провести опыт, можно видеть, что на Земле предмет падает с высоты 20м за 2.02с. Откуда следует, что скорость падения составляет:
Выходит, что через полсекунды после начала падения предмет окажется на 5м ниже, чем исходная точка, через секунду – на 9.9м ниже.
Однако, проведя реальное измерение, можно убедиться, что это совсем не так. За первую секунду предмет пройдет только 4.9м. А за первые полсекунды – всего лишь 1.23м ! Если же высота падения будет больше, то за три секунды путь составит не 29.7м, как следует из формулы, а больше 40м !
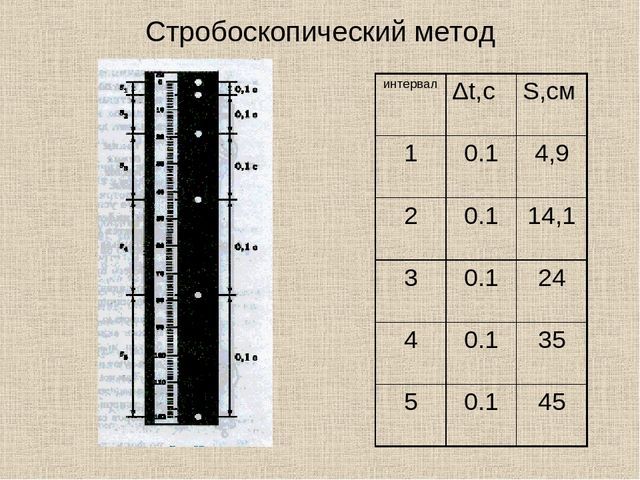
Причина такого расхождения с расчетом состоит в том, что предмет под действием тяготения Земли движется неравномерно, постоянно изменяя скорость. И на каком бы участке мы не измерили его скорость – полученное значение будет различно, и его невозможно будет использовать в расчетах и уравнениях для других участков.
Свести неравномерное движение к равномерному невозможно.
Видео:УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать

Мгновенная скорость
Описанное затруднение можно разрешить, если учесть, что движение – процесс непрерывный. Ни координаты точки, ни ее скорость не могут изменяться скачками. Во время движения точка проходит все бесчисленное множество координат пути, на всем пути скорость ее непрерывно изменяется в некотором диапазоне, и при этом, чем меньше рассматриваемый отрезок времени, тем меньше будет изменение координаты и скорости.
Рассмотрим падение предмета, начиная с конца первой секунды. В этот момент координата будет равна 4.905м. Отметим новую координату падающего предмета через небольшое время, и вычислим скорость:
Видео:Средняя и мгновенная скоростиСкачать

Как рассчитать мгновенную скорость, формулу мгновенной скорости
Мгновенная скорость сообщает нам о движении частицы в определенный момент времени в любом месте на ее пути.
Мгновенная скорость принимается за предел средней скорости при стремлении времени к нулю. Вычислять Vинст мы можем использовать график смещения-времени / формулу мгновенной скорости. т.е. производная смещения (s) по времени (t), взятая.
Чтобы узнать, как рассчитать мгновенную скорость объекта, нам нужно выполнить следующие действия. . Давайте посмотрим на это на примере.
Видео:Мгновенная скоростьСкачать

Рассмотрим уравнение скорости в терминах положения / смещения.
Вычислять мгновенная скорость, мы должны рассмотреть уравнение это говорит нам о его должность ‘s’ в определенный время ‘t’. Это означает, что уравнение должно содержать переменную ‘s‘с одной стороны и’t‘ с другой стороны,
s = -2т 2 + 10т +5 при t = 2 секунды.
В этом уравнении переменными являются:
Смещение = s, измеряется в метрах.
Время = t, измеряется в секундах.
Видео:Урок 24. Мгновенная скорость. Равноускоренное движение. УскорениеСкачать

Рассмотрим производную данного уравнения.
Чтобы найти производную данного уравнения перемещения, дифференцировать функцию по времени,
ds / dt = — (2) 2т (2-1) + (1) 10 т 1 – 1 + (0) 5 т 0
ds / dt = -4т 1 + 10т 0
ds / dt = -4t + 10
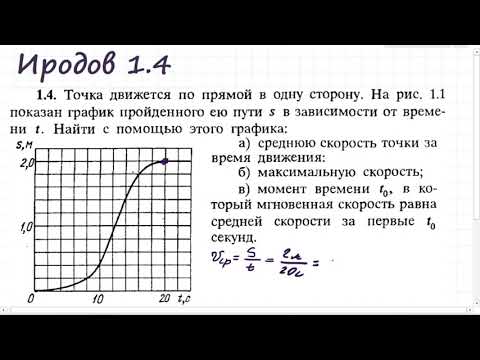
Видео:Определение средней и мгновенной скорости по графику: Иродов 1.4Скачать
Подставьте данное значение «t» в уравнение производной, чтобы найти мгновенную скорость.
Найдите мгновенная скорость при t = 2 подставить «2» для t в производной ds / dt = -4t + 10. Тогда мы можем решить уравнение
ds / dt = -4 (2) + 10
ds / dt = -8 + 10
ds / dt = -2 метра в секунду
Здесь «метры / секунда» — это единица измерения мгновенной скорости в системе СИ.
Видео:Урок 16 (осн) Средняя скорость. Вычисление пути и времени движенияСкачать

Как рассчитать Instantaneo скорость нас из графика
Мгновенная скорость в любой конкретный момент времени определяется наклоном касательной, проведенной к графику положения-времени в этой точке.
- Постройте график расстояние против времени.
- Отметьте точку, в которой вам нужно найти мгновенную скорость, скажем A.
- Определите точку на графике, соответствующую времени t1 и t2.
- Вычислить vсредний и проведем касательную в точке A.
- На графике vинст в точке A находится по касательной, проведенной в этой точке
- Чем длиннее тангенс, тем точнее будут значения.
- На показанном изображении Синяя линия это график зависимости положения от времени, А Красная линия — приблизительный наклон линии при t = 2.5 секунды.
- Если мы продолжаем выбирать точки, которые все ближе и ближе друг к другу, линия начнет приближаться к наклону линии, касательной к одной точке.
- Если мы возьмем предел функции в этой точке, мы получим значение наклона касательной в этой точке.
- Расстояние составляет примерно 140 м, а временной интервал — 4.3 с. Следовательно, приблизительный уклон составляет 32.55 м / с.
Видео:Закон Сложения Скоростей - Относительная скорость / Урок Физики 10 класс / КинематикаСкачать

Как рассчитать мгновенную скорость по графику положения-времени.
Для вычисления мгновенной скорости по графику положения-времени.
Видео:Физика - уравнения равноускоренного движенияСкачать

Постройте график зависимости смещения от времени.
- Используйте оси X и Y для представления время и перемещение.
- Затем нанесите на график значения времени и смещения.
Видео:Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

Выберите любые две точки на графике st.
- Линия смещения содержит точки (3,6) и (5,8).
- В этом примере, если мы хотим найти наклон в точке (3,6), мы можем установить А = (3,6) и B=(5,8)
Видео:Мгновенная скорость (видео 6) | Векторы. Прямолинейное движение | ФизикаСкачать

Найдите наклон линии, соединяющей две точки, т. Е. Между точками A и B.
Найдите среднюю скорость между этими двумя временными интервалами, т. Е.
где K — наклон между двумя точками.
Здесь наклон между A и B равен:
Видео:Мгновенный центр вращенияСкачать

Повторите несколько раз, чтобы найти уклон, перемещая B ближе к A.
- Продолжайте выбирать точки ближе друг к другу; затем он начнет приближаться к наклону касательной.
- Если мы рассмотрим предел функции в этой точке, мы получим значение наклона в этой точке.
- Здесь мы можем использовать точки (4,7.7), (3.5, 6.90) и (3.25, 6.49) для B и исходную точку (3,6) для A.
Видео:Задача на среднюю скоростьСкачать

Вычислите наклон для бесконечно малого отрезка касательной.
В этом примере, когда мы приближаем B к A, мы получаем значения 1.7, 1.8 и 1.96 для K. Поскольку эти числа примерно равны 2, можно сказать, что 2 — наклон А.
Здесь, мгновенная скорость 2 м / с.
Видео:003 Мгновенная скоростьСкачать

Формула мгновенной скорости
С математической точки зрения мы можем написать формула мгновенной скорости в виде,
Здесь, ds / dt — это производная смещения (с) по времени (t).
Приведенные выше производная имеет конечное значение когда и знаменатель, и числитель стремятся к нулю.
Видео:Уравнение движения тела дано в виде x=2−3t. ВычислиСкачать

Расчет формулы мгновенной скорости
Используя вычисления, всегда можно вычислить скорость объекта в любой момент на его пути. Это называется мгновенной скоростью. и задается уравнением v = ds / dt .
Мгновенная скорость = предел, поскольку изменение во времени приближается к нулю (изменение положения / изменение во времени) = производная смещения по времени
Видео:Урок 34. Свободное падение. Ускорение свободного паденияСкачать

Формула средней и мгновенной скорости
| Формула | Символ | Определение | |
| Средняя скорость | sf = Окончательный смещение si = Начальное смещение | Средняя скорость is общее расстояние деленное на общее затраченное время. | |
| Мгновенная скорость | Скорость при любом момент времени. |
Видео:Скорость прямолинейного равноускоренного движения. График скорости | Физика 9 класс #6 | ИнфоурокСкачать

Формула мгновенной угловой скорости
мгновенная угловая скорость скорость, с которой частица движется по круговой траектории в определенный момент времени.
мгновенная угловая скорость вращающегося объекта определяется выражением
dθ/dt = производная углового положения θ по времени, найденное предельным переходом Δ t → 0 в средняя угловая скорость.
направление угловой скорости на круговой траектории — вдоль оси вращения и указывает от вас на вращающееся тело по часовой стрелке и к вам для тела, вращающегося против часовой стрелки. В математике это обычно описывается правило правой руки.
Формула мгновенной скорости и скорости
Формула мгновенной скорости
Формула мгновенной скорости
Разница между мгновенной скоростью и мгновенной скоростью.
| Мгновенная скорость | Мгновенная скорость |
| Это скорость движущейся частицы в определенный момент t. | Вход в музей Мадам Тюссо мера скорости частицы в определенный момент t. |
| Мгновенная скорость определяет, насколько быстро и в каком направлении движется объект. | Мгновенная скорость измеряет, насколько быстро частица движется. |
| Количество векторов | Скалярная величина |
Определение и формула мгновенной скорости
Определение мгновенной скорости
Мгновенная скорость описывается как скорость движущегося объекта. Мы можем найти его, используя среднюю скорость, но мы должны сузить время, чтобы приблизиться к нулю.
Итого можно сказать, что мгновенная скорость — это скорость движущейся частицы в определенный момент времени.
Формула мгновенной скорости
Для любого уравнения движения s(t), для мгновенная скорость когда t приближается к нулю, мы можем записать формула в виде,
Мгновенная скорость формула предела
Мгновенная скорость любого объекта — это предел средней скорости, когда время приближается к нулю..
Вставьте значения t1= t и t2 = t + Δt в уравнение для средней скорости и переходя к пределу при Δt → 0, находим формула предела мгновенной скорости
Как найти мгновенную скорость на графике
Мгновенная скорость равна наклону касательной на графике положение-время.
Мгновенно s Интерпретация скорости из графика st
- Мгновенная скорость равна наклону касательной на графике положение-время.
- Интерпретация мгновенной скорости по графику st
- Наклон фиолетовой линии (касательной) на графике смещения v / s дает мгновенную скорость.
- Если фиолетовая линия образует угол с положительной осью абсцисс.
Vinst = наклон фиолетовой линии = tanθ
Как найти мгновенную скорость из средней скорости
Для того, чтобы найти мгновенная скорость в точке, мы должны сначала найти среднюю скорость в этой точке.
Вы можете найти мгновенную скорость при t = a с помощью вычисление средней скорости графика зависимости положения от времени путем взятия меньшего и большего приращения точки, в которой вы хотите определить V inst .
Пример мгновенной скорости
Во время езды на велосипеде велосипедист меняет свою скорость в зависимости от расстояния и времени, которое он проходит.
Если мы хотим найти скорость в одной конкретной точке, мы должны использовать мгновенную скорость.
Покажи нам пример,
а). Определить мгновенную скорость частицы, движущейся по прямому пути за t = 2 секунды, с функцией положения «s», определенной как 4t² + 2t + 3?
Решение:
Данный с = 4т² + 2т + 3
Дифференцируя данную функцию по времени, мы вычисляем мгновенную скорость следующим образом:
Подставляя значение t = 2, мы получаем мгновенную скорость как,
Подставляя функцию s,
Таким образом, мгновенная скорость для вышеуказанной функции составляет 18 м / с.
Проблема мгновенной скорости
Некоторые проблемы с мгновенной скоростью,
Проблема 1:
Движение тележки задается функцией s = 3t 2 + 10t + 5. Вычислите его мгновенную скорость в момент времени t = 4 с.
Решение:
Данная функция s = 3t 2 + 10т + 5.
Продифференцируя указанную выше функцию по времени, получим
Подставляя функцию s,
[v_ = v (t) = 6t + 10]
Подставляя значение t = 4 с, мы получаем мгновенную скорость как,
Для данной функции мгновенная скорость составляет 34 м / с.
Проблема 2:
Выстреленная пуля движется по прямой траектории, и ее уравнение движения имеет вид S (t) = 3t + 5t. 2 . Так, например, если он летит за 12 секунд до удара, найдите мгновенную скорость при t = 7 с.
Решение: Мы знаем уравнение движения:
Проблема 3:
Объект выпускается с определенной высоты, чтобы он мог свободно падать под действием силы тяжести. Уравнение движения для перемещения s (t) = 5.1 т. 2 . Какой будет мгновенная скорость объекта в момент времени t = 6 с после выпуска?
Решение:
Мгновенная скорость при t = 6 с
Проблема 4:
Найдите скорость при t = 2, учитывая уравнение перемещения s = 3t 3 — 3т 2 + 2т + 7.
Решение:
Это похоже на предыдущие задачи, за исключением того, что они дали кубическое уравнение вместо квадратного уравнения, чтобы решить его таким же образом.
s (t) = 3t 3 — 3т 2 + 2т + 7.
Мгновенная скорость при t = 7 с
Проблема 5:
Положение человека, движущегося по прямой, определяется выражением s (t) = 7t. 2 + 3t + 19, где t — время (секунды). Найдите уравнение для мгновенной скорости v (t) частицы в момент времени t.
Решение:
Дано: s (t) = 7t 2 + 3т + 19
vинст = v (t) = (14t + 3) м / с — уравнение для мгновенной скорости.
Предположим, что если принять t = 3s, то
Проблема 6:
Движение автомобиля описывается уравнением движения s = gt 2 + b, где b = 20 м и g = 12 м. Следовательно, найдите мгновенную скорость при t = 4 с.
Решение:
Здесь g = 12 и t = 4s,
v (4) = [2 x 12 x 4] = 96 м / с.
v (т) = 96 м / с.
Проблема 7:
Стол, упавший со здания 1145 футов, имеет высоту (в футах) над землей, определяемую как s (t) = 1145-12 т. 2 . Затем вычислите мгновенную скорость стола на 3 с?
Решение:
Мгновенная скорость при t = 3 с составляет -72 м / с.
Проблема 8:
Функция положения частиц определяется выражением s = (3t 2 )i — (4т)k + 2. какова его мгновенная скорость при t = 2? Каково его мгновенное ускорение как функция времени?
Решение:
Чтобы вычислить мгновенное ускорение как функцию времени
дифференцируя уравнение 1 по t, получаем
Проблема 9:
Положение насекомого определяется как s = 44 + 20t — 3t. 3 , где t в секундах, а s в метрах .
а. Найдите среднюю скорость объекта между t = 0 и t = 4. s.
б. В какое время между 0 и 4 мгновенная скорость равна нулю.
решение:
Для расчета средней скорости
Чтобы найти время, при котором мгновенная скорость равна нулю.
Проблема 10:
Частица движется с функцией смещения s = t 2 + 3 .
Найдите положение при t = 2.
Найдите среднюю скорость от t = 2 до t = 3.
Найти его мгновенную скорость при t = 2 .
Решение:
Чтобы найти позицию при t = 2
с (2) = 7
Для того, чтобы найти Средняя скорость.
Чтобы найти мгновенную скорость
При t = 2 с
Мгновенная скорость в зависимости от средней скорости
| Мгновенная скорость | Средняя скорость |
| мгновенная скорость — средняя скорость между двумя точками. | Средняя скорость это соотношение изменения дистасть относительно времени за период. |
| Мгновенная скорость рассказывает о движении между двумя точками на пройденном пути. | Средняя скорость не дает информации о движении между точками. Путь может быть прямым / изогнутым, а движение может быть постоянным / переменным. |
| Мгновенная скорость равен наклону касательной к смещение (с) в зависимости от графика времени. | Он равен наклону секущая линия of граф st. |
| вектор | вектор |
Как найти мгновенная скорость без исчисления
Wмы можем найти мгновенную скорость приближением по график зависимости смещения от времени без исчисления в определенной точке. Нам нужно провести касательную в точке вдоль изогнутой линии и оценить наклон, где вам нужно найти мгновенную скорость.
Как рассчитать мгновенную скорость и мгновенное ускорение
| Мгновенная скорость | Мгновенное ускорение | |
| Из формулы | Для расчета мгновенной скорости, возьмем предел изменения расстояния по времени, когда время приближается к нулю. т. е. взяв первая производная функции смещения. | к рассчитать мгновенное ускорение, принять предел изменения скорости по времени, когда изменение во времени приближается к нулю. т.е. взяв вторая производная функции смещения. |
| Из графика | Равно наклон касательной к графику st. | Равно наклон касательной графика vt. |
11 задачи:
Пуля, выпущенная в космос, движется по прямой траектории, и ее уравнение движения имеет вид s (t) = 2t + 4t 2 . Если он движется в течение 12 секунд до удара, найдите мгновенную скорость и мгновенное ускорение в момент времени t = 3 секунды.
Решение: Мы знаем уравнение движения: s (t) = 2t + 4t 2
Как найти мгновенную скорость и скорость
Мгновенная скорость задается как величина мгновенной скорости.
Если известно смещение как функция времени, мы можем узнать мгновенную скорость в любое время.
Давайте разберемся в этом на примере.
12 задачи:
Уравнение движения s (t) = 3t 3
Рассмотрим t = 2s
Почему можно рассчитать мгновенную скорость по кинематическим формулам только при постоянном ускорении
Уравнения кинематики можно использовать только при постоянном ускорении объекта.
В случае переменные ускорения, Уравнения кинематики будут разными в зависимости от функции, которую принимает ускорение; в то время; мы должны использовать Комплексный подход вычислять мгновенная скорость. Что будет немного сложно.
Почему при вычислении мгновенной скорости мы берем небольшие промежутки времени. Как он дает скорость в этот момент, если мы рассчитываем ее за определенный промежуток времени?
мгновенная скорость дан кем-то ,
Чем меньше значение «t», Тем точнее будет наклон касательной, т. е. мгновенная скорость.
Когда ты хочешь рассчитать скорость в определенное время вам нужно сначала рассчитать средние скорости взяв небольшие промежутки времени. Если эти средние скорости дают одно и то же значение, тогда это будет требуемый мгновенная скорость.
Различаются ли скорость и мгновенная скорость?
Мгновенная скорость отличается от скорости.
Скорость обычно известен как скорость изменения положения во времени. Напротив, в мгновенная скорость, временной интервал сужается, чтобы приблизиться к нулю, чтобы получить скорость в конкретный момент времени.
Например,
Частица движение по кругу имеет нулевые смещения, и требуется знать скорость частицы. В этом случае мы можем вычислить мгновенную скорость, потому что она имеет тангенциальная скорость в любой момент времени.
Что такое мгновенная скорость на реальных примерах
Реальные примеры мгновенной скорости
Если мы рассмотрим пример мяча для сквоша, мяч возвращается в исходную точку; в это время полное смещение и средняя скорость будут равны нулю. В таких случаях движение рассчитывается по формуле мгновенная скорость.
- Спидометр автомобиля дает информацию о мгновенная скорость / скорость средство передвижения. Он показывает скорость в определенный момент времени.
- Во время гонки фотографы делают снимки бегунов, их средняя скорость не меняется, но меняется их мгновенная скорость, зафиксированная на «снимках». Так что это будет пример мгновенной скорости.
- Если вы находитесь рядом с магазином, и перед вами проехал автомобиль на отметке «t«Во-вторых, и вы начинаете думать о его скорости на конкретном время, здесь вы имели бы в виду мгновенная скорость транспортного средства.
Часто задаваемые вопросы | FAQs
Является ли мгновенная скорость вектором
Мгновенная скорость — это векторная величина.
Мгновенная скорость — это вектор, потому что он имеет как величину, так и направление. Он показывает как скорость (относится к величине), так и направление. участникале Имеет размер LT -1 Мы можем определить это, взяв наклон графика расстояние-время..
Как найти мгновенную скорость только с графиком положения и времени и без заданного уравнения
Мы можем определить мгновенную скорость, взяв наклон графика положения-времени.
- Постройте график смещения во времени.
- Выберите точку A и другую точку B, которая находится рядом с точкой A на линии.
- Найдите угол наклона между A и B, рассчитайте несколько раз, перемещая A ближе к B.
- Рассчитайте наклон для бесконечно малого интервала на прямой.
- Полученный наклон представляет собой мгновенную скорость.
Можно ли мгновенно изменить скорость
Невозможно вызвать мгновенное изменение скорости, так как для этого потребуется бесконечное ускорение.
Как правило, ускорение является результатом F = ma
а скорость является результатом ускорения (от интегрирования). Если изменение скорости является ступенчатой функцией и когда время приближается к нулю, потребуется бесконечное ускорение и сила, чтобы мгновенно изменить скорость массы.
Как я могу рассчитать смещение, если ускорение является функцией мгновенной скорости Задана начальная скорость
Мы можем вычислить смещение двумя способами, когда задана начальная скорость.
От происхождения
Здесь ускорение является функцией мгновенной скорости,
Начальная скорость
Интегрируя,
Используя эту форму, вы можете получить ds смещения.
Из формулы
Используя приведенное ниже кинематическое уравнение, мы можем найти смещение,
Что такое средний и мгновенная скорость
Средняя скорость и мгновенная скорость выражаются следующим образом:
| Средняя скорость | Мгновенная скорость |
| Средняя скорость для определенного временного интервала — это полное смещение, деленное на общее время. | И временной интервал, и смещение в какой-то момент приближаются к нулю. Но предел производной смещения по общему интервалу времени отличен от нуля и называется мгновенной скоростью. |
| Средняя скорость это скорость всего пути в движении | а мгновенная скорость скорость частицы в определенный момент времени |
| v avg = s/t | v inst = ds/dt |
Мгновенное ускорение перпендикулярно мгновенной скорости
Мгновенное ускорение тела всегда перпендикулярно мгновенной скорости.
При круговом движении мгновенное ускорение тела всегда перпендикулярно мгновенной скорости, и это ускорение называется центростремительным ускорением. Скорость остается неизменной; только направление меняется, поскольку перпендикулярное ускорение изменяет траекторию тела.
Последние выпуски передовой науки и исследований