Как определить линейную зависимость уравнений (2 видео)

Линейно зависимые и линейно независимые функции. Примеры исследования функций на линейную зависимость по определению.

Функции $y_1(x),;y_2(x),;y_3(x),ldots,y_n(x)$ называются линейно зависимыми на некотором множестве $T$, если существуют такие константы $alpha_1,;alpha_2,;alpha_3,ldots,alpha_n$, что $forall xin T$ выполняется следующее равенство:

$$ begin alpha_1cdot y_1+alpha_2cdot y_2+ldots+alpha_ncdot y_n=0 end $$

Примечание к терминологии: показатьскрыть

В определении использован термин «равенство», хотя можно было бы воспользоваться термином «тождество». Фразы «для каждого значения переменной $xin T$ выполняется равенство $a(x)=b(x)$» и «на множестве $T$ верно тождество $a(x)equiv b(x)$» равносильны. Например, фраза «равенство $sin^2x=1-cos^2x$ выполнено для $forall xin R$», равносильна такой: «на множестве $R$ верно тождество $sin^2x=1-cos^2x$». Т.е. вместо слов о том, что «$forall xin T$ выполняется следующее равенство: $alpha_1cdot y_1+alpha_2cdot y_2+ldots+alpha_ncdot y_n=0$» можно сказать так: «на множестве $T$ верно тождество $alpha_1cdot y_1+alpha_2cdot y_2+ldots+alpha_ncdot y_nequiv 0$». Некоторые авторы предпочитают использовать именно термин «тождество».

Условие (2) можно изложить и в такой формулировке: среди коэффициентов $alpha_i$ есть хотя бы один, не равный нулю.

Несложно убедиться в равносильности формулировок. Равенство $alpha_^+alpha_^+ldots+alpha_^=0$ возможно в том и только в том случае, когда $alpha_1=alpha_2=ldots=alpha_n=0$. Если же $sum_^alpha_^neq 0$, то равенство $alpha_1=alpha_2=ldots=alpha_n=0$ не выполнено, т.е. хотя бы один из коэффициентов $alpha_i$ отличен от нуля.

Если же равенство (1) возможно лишь при условии:

то функции $y_1(x),;y_2(x),;y_3(x),ldots,y_n(x)$ именуют линейно независимыми на множестве $T$. По сути, условие (3) равносильно такому: все коэффициенты $alpha_i$ равны нулю.

Для двух функций несложно вывести простое правило: если $forall xin T$ $fracneq const$ на некотором интервале $T=(a;b)$, то функции $y_1(x)$ и $y_2 (x)$ линейно независимы на $T$. Если же $forall xin T$ $frac= const$ на $T$, то функции $y_1(x)$ и $y_2 (x)$ линейно зависимы на $T$.

Обоснование этого правила: показатьскрыть

Допустим, что $fracneq const$ на $T$, однако функции $y_1(x)$ и $y_2 (x)$ линейно зависимы. Если функции линейно зависимы, то существуют такие константы $alpha_1$ и $alpha_2$, не равные нулю одновременно, что выполняется равенство: $alpha_1cdot y_1+alpha_2cdot y_2=0$. Пусть, к примеру, $alpha_1neq 0$. Тогда, с учетом $y_2 (x)neq 0$ на $T$, получим: $frac=-frac=const$, что противоречит допущению $fracneq const$.

Если же $frac= const$, то $y_1(x)-Ccdot y_2(x)=0$ на $T$, т.е. $alpha_1=1;;alpha_2=-C$. При этом $alpha_^+alpha_^=1+C^2neq 0$, т.е. функции $y_1(x)$ и $y_2 (x)$ линейно зависимы на $T$.

Все примеры, указанные в этой теме, будут опираться на определения и свойство, приведенные выше. Естественно, что в общем случае применение таких определений несколько затруднительно. Существует несколько критериев, которые позволяют упростить процесс проверки функций на линейную зависимость. На сайте рассмотрены два таких способа: с помощью определителя Вронского и определителя Грама.

Выяснить, являются ли функции $y_1(x)=x^2+2x-4$, $y_2(x)=-4x^2+7x-1$, $y_3(x)=-5x^2+20x-14$ линейно зависимыми или линейно независимыми на множестве $R$.

Рассмотрим линейную комбинацию этих функций: $alpha_1cdot y_1+alpha_2cdot y_2+alpha_3cdot y_3$. Если $forall xin R$ равенство $alpha_1cdot y_1+alpha_2cdot y_2+alpha_3cdot y_3=0$ выполняется только при $alpha_1=alpha_2=alpha_3=0$, то рассматриваемые функции линейно независимы. Если же $forall xin R$ равенство $alpha_1cdot y_1+alpha_2cdot y_2+alpha_3cdot y_3=0$ возможно при условии, что хотя бы один из коэффициентов $alpha_i$ не равен нулю, то функции линейно зависимы.

Подставим в выражение $alpha_1cdot y_1+alpha_2cdot y_2+alpha_3cdot y_3=0$ заданные функции:

Раскроем скобки и перегруппируем слагаемые:

$$ alpha_1cdot x^2+2alpha_1cdot x-4alpha_1-4alpha_2cdot x^2+7alpha_2cdot x-alpha_2-5alpha_3cdot x^2+20alpha_3cdot x-14alpha_3=0; $$ $$(alpha_1-4alpha_2-5alpha_3)cdot x^2+(2alpha_1+7alpha_2+20alpha_3)cdot x+(-4alpha_1-alpha_2-14alpha_3)=0.$$

Последнее равенство возможно лишь в том случае, когда коэффициенты при степенях переменной $x$ одновременно равны нулю, т.е.:

Мы получили однородную систему линейных уравнений. Нам нет необходимости в её решении, нужно лишь установить количество решений. Если решение лишь одно – нулевое (или, в иной терминологии, тривиальное), т.е. $alpha_1=alpha_2=alpha_3=0$, то функции линейно независимы. Если же есть иные решения, кроме нулевого, то функции линейно зависимы. Найдем ранг матрицы системы $A= left( begin 1 & -4& -5\ 2 & 7& 20 \ -4& -1& -14 end right)$ и ранг расширенной матрицы системы: $tilde= left( begin 1 & -4& -5& 0\ 2 & 7& 20 & 0 \ -4& -1& -14 & 0 end right)$, а затем применим теорему Кронекера-Капелли.

Отсюда получаем решение: $left< begin&alpha_1=-3alpha_3;\&alpha_2=-2alpha_3;\&alpha_3=alpha_3;;alpha_3 in R end right.$ Например, подставив $alpha_3=-1$, получим: $alpha_1=3;; alpha_2=2$. Несложно убедиться непосредственной проверкой, что равенство $alpha_1cdot y_1+alpha_2cdot y_2+alpha_3cdot y_3=0$ при найденных коэффициентах будет выполнено $forall xin R$:

$$ 3cdot y_1+2cdot y_2-y_3=3cdot(x^2+2x-4)+2cdot(-4x^2+7x-1)-(-5x^2+20x-14)=0. $$

Итак, существуют такие константы $alpha_1;;alpha_2;;alpha_3$ (например, $alpha_1=3;;alpha_2=2;;alpha_3=-1$), не все одновременно равные нулю, что на $R$ выполняется тождество $alpha_1cdot y_1+alpha_2cdot y_2+alpha_3cdot y_3equiv 0$. Следовательно, рассматриваемые функции линейно зависимы.

Исследовать на линейную зависимость такие функции: $y_1(x)=xln(x+4);;y_2(x)=ln^2(x+4)$.

Исследование проведем в интервале $T=(-4;+infty)$, который представляет собой область определения заданных функций. Применим правило для определения линейной зависимости двух функций, указанное в начале страницы. Так как при $xin(-4;+infty)$ имеем: $frac=fracneq const$, то данные функции линейно независимы на $T=(-4;+infty)$.

Исследовать на линейную зависимость функции: $y_1(x)=1$, $y_2(x)=x$, $y_3(x)=x^2$, $y_4(x)=x^3$, $y_5(x)=x^4$.

Область определения этих функций есть вся числовая прямая, т.е. $x in R$. Рассмотрим равенство:

$$ begin alpha_1cdot 1+alpha_2cdot x+alpha_3cdot x^2+alpha_4cdot x^3+alpha_5cdot x^4=0 end $$

Если равенство (4) для всех $xin R$ возможно лишь при условии $alpha_1=alpha_2=alpha_3=alpha_4=alpha_5=0$, то заданные функции линейно независимы. Если же равенство (4) $forall xin R$ выполняется на наборе констант $alpha_1$, $alpha_2$, $alpha_3$, $alpha_4$, $alpha_5$, среди которых хотя бы одна отлична от нуля, то заданные функции линейно зависимы. Итак, нужно исследовать равенство (4).

В левой части равенства (4) расположен многочлен, порядок (или, в иной терминологии, степень) которого не превышает $4$. Например, если $alpha_1=2; ;alpha_2=0;;alpha_3=0;;alpha_4=7;;alpha_5=0$, то получим многочлен третьего порядка:

$$alpha_1cdot 1+alpha_2cdot x+alpha_3cdot x^2+alpha_4cdot x^3+alpha_5cdot x^4=7x^3+2.$$

Т.е. в левой части равенства (4) может быть многочлен четвертого, третьего, второго, первого и нулевого порядков.

Рассмотрим случай, когда в левой части равенства (4) расположен многочлен, порядок которого не равен нулю (среди констант $alpha_2;;alpha_3;;alpha_4;;alpha_5$ хотя бы одна не равна нулю). Любой многочлен первого порядка может обратиться в ноль только в одной точке (т.е. существует только одно значение $x$, при котором многочлен первого порядка равен нулю). Многочлен второго порядка равен нулю не более, чем в двух точках; многочлен третьего порядка – не более, чем в трёх точках; многочлен четвертого порядка обращается в ноль не более, чем в четырёх точках. Т.е. если среди констант $alpha_2;;alpha_3;;alpha_4;;alpha_5$ есть хотя бы одна, отличная от нуля, то равенство (4) может быть выполнено не более, чем при четырёх значениях $x$ (а не для всех $xin R$).

Рассмотрим ситуацию, когда среди констант $alpha_2;;alpha_3;;alpha_4;;alpha_5$ нет ни одной, отличной от нуля, т.е. $alpha_2=alpha_3=alpha_4=alpha_5=0$. В этом случае в левой части равенства (4) получим многочлен нулевого порядка:

$$alpha_1cdot 1+alpha_2cdot x+alpha_3cdot x^2+alpha_4cdot x^3+alpha_5cdot x^4=alpha_1$$

А само равенство (4) станет таким: $alpha_1=0$. Следовательно, для многочлена нулевого порядка выполнение равенства (4) возможно лишь при $alpha_1=alpha_2=alpha_3=alpha_4=alpha_5=0$.

Подведём итоги: если в правой части равенства (4) стоит многочлен ненулевого порядка, то равенство (4) не может быть выполнено при всех $xin R$. Равенство (4) может быть выполнено для всех $xin R$ только когда в правой части стоит многочлен нулевого порядка, однако это означает $alpha_1=alpha_2=alpha_3=alpha_4=alpha_5=0$. Так как равенство (4) выполняется для всех $xin R$ только при условии $alpha_1=alpha_2=alpha_3=alpha_4=alpha_5=0$, то заданные функции линейно независимы на $R$.

Исследовать на линейную зависимость функции: $y_1(x)=4$, $y_2(x)=arcsin$, $y_3(x)=arccos$ на отрезке $[-1;1]$.

Так как $arcsin x+arccos x=frac ; forall x in [-1;1]$ то:

$$arcsin x+arccos x=fraccdot4; ; arcsin x+arccos x-fraccdot4=0; ; 1cdot y_1+1cdot y_2+left(-fracright)cdot y_3=0$$

Итак, существует такой набор констант $alpha_1; ; alpha_2;; alpha_3$ (например, $alpha_1=1;; alpha_2=1;; alpha_3=-frac$), среди которых есть хотя бы одна константа, отличная от нуля, что равенство $alpha_1cdot y_1+alpha_2cdot y_2+alpha_3cdot y_3=0$ будет выполнено для всех $xin[-1;1]$. Это означает, что функции $y_1(x)=4$, $y_2(x)=arcsin$, $y_3(x)=arccos$ линейно зависимы на отрезке $[-1;1]$.

Исследовать на линейную зависимость функции: $y_1(x)=x;; y_2(x)=|x|$ в их области определения.

Областью определения заданных функций есть все множество действительных чисел, т.е. $xin R$. Функции будут линейно зависимыми, если существует такой набор констант $alpha_1$ и $alpha_2$, что для всех значений $xin R$ выполнено равенство $alpha_1cdot y_1+alpha_2cdot y_2=0$ (т.е. $alpha_1cdot x+alpha_2cdot |x|=0$), причем хотя бы один из коэффициентов ($alpha_1$ или $alpha_2$) не равен нулю. Если же выполнение равенства $alpha_1cdot y_1+alpha_2cdot y_2=0$ при $forall xin R$ возможно лишь при $alpha_1=alpha_2=0$, то заданные функции будут линейно независимыми. Рассмотрим равенство $alpha_1cdot x+alpha_2cdot |x|=0$ подробнее.

Если $x≥ 0$, то $|x|=x$, поэтому равенство $alpha_1cdot x+alpha_2cdot |x|=0$ станет таким: $alpha_1cdot x+alpha_2cdot x=0$, $xcdot(alpha_1+alpha_2)=0$. Равенство $xcdot(alpha_1+alpha_2)=0$ должно быть выполнено при всех $x≥ 0$, поэтому $alpha_1+alpha_2=0$.

Итак, чтобы равенство $alpha_1cdot x+alpha_2cdot |x|=0$ было верным для всех $xin R$, требуется выполнение двух условий:

Полученная система имеет лишь тривиальное (нулевое) решение: $alpha_1=alpha_2=0$. Итак, выполнение равенства $alpha_1cdot x+alpha_2cdot |x|=0$ при $forall xin R$ возможно лишь в случае $alpha_1=alpha_2=0$, поэтому функции линейно независимы на R.

Исследование на линейную зависимость с помощью определителей Вронского и Грама указаны в дальнейших темах сайта.

Заметили ошибку, опечатку, или некорректно отобразилась формула? Отпишите, пожалуйста, об этом в данной теме на форуме (регистрация не требуется).

Содержание

Линейная независимость функций. Определители Вронского и Грама
Линейная зависимость системы векторов. Коллинеарные векторы
Коллинеарные векторы
Условия коллинеарности векторов
Примеры задач на исследование коллинеарности векторов
Критерии линейной зависимости и линейной независимости систем векторов
Свойства линейно зависимых векторов
Примеры решения задач на линейную зависимость или линейную независимость векторов
💥 Видео

Видео:Линейная зависимость векторовСкачать

Линейная независимость функций. Определители Вронского и Грама

Пусть имеем конечную систему из функций , определенных на интервале . Функции называют линейно зависимыми на интервале , если существуют постоянные , не все равные нулю, такие, что для всех значений из этого интервала справедливо тождество

Если же это тождество выполняется только при , то функции называют линейно независимыми на интервале .

Пример 1. Показать, что система функций линейно независима на интервале .

Решение. В самом деле, равенство может выполняться для всех только при условии, что . Если же хоть одно из этих чисел не равно нулю, то в левой части равенства будем иметь многочлен степени не выше третьей, а он может обратиться в ноль не более, чем при трех значениях из данного интервала.

Пример 2. Показать, что система функций , где попарно различны, линейно независима на интервале .

Решение. Предположим обратное, т. е. что данная система функций линейно зависима на этом интервале. Тогда

на интервале , причем, по крайней мере, одно из чисел отлично от нуля, например . Деля обе части тождества (1) на , будем иметь

Дифференцируя тождество, получаем

Делим обе части тождества (2) на :

Дифференцируя (3), получаем , что невозможно, так как по предположению, по условию, а .

Наше предположение о линейной зависимости данной системы функций привело к противоречию, следовательно, эта система функций линейно независима на интервале , т.е. тождество (1) будет выполняться только при .

Пример 3. Показать, что система функций , где , линейно независима на интервале .

Решение. Определим значения и , при которых будет выполняться тождество

Разделим обе его части на :

Подставляя в (5) значение , получаем и, значит, ; но функция не равна тождественно нулю, поэтому . Тождество (5) и, следовательно, (4) имеют место только при , т. е. данные функции линейно независимы в интервале .

Замечание. Попутно доказана линейная независимость тригонометрических функций .

Пример 4. Доказать, что функции

линейно зависимы в интервале .

Решение. Покажем, что существуют такие числа , не все равные нулю, что в интервале справедливо тождество

Предполагаем тождество (7) выполненным; положим, например, . Тогда получим однородную систему трех уравнений с тремя неизвестными

Определитель этой системы трёх уравнений с тремя неизвестными равен нулю:

Следовательно, однородная система (8) имеет ненулевые решения, т. е. существуют числа , среди которых имеется по крайней мере одно отличное от нуля. Для нахождения такой тройки чисел возьмем, например, два первых уравнения системы (8):

Из первого уравнения имеем , из второго . Полагая , получим ненулевое решение системы (8):

Покажем теперь, что при этих значениях тождество (7) будет выполняться для всех . Имеем

каково бы ни было . Следовательно, система функций (6) линейно зависима на интервале .

Замечание. Для случая двух функций можно дать более простой критерий линейной независимости. Именно, функции и будут линейно независимыми на интервале , если их отношение не равно тождественной постоянной на этом интервале; если же , то функции будут линейно зависимыми.

Пример 5. Функции и линейно независимы в интервале , так как их отношение в этом интервале.

Пример 6. Функции и линейно зависимы в интервале , так как их отношение в этом интервале (в точках разрыва функции доопределяем это отношение по непрерывности).

Пусть функций имеют производные (n–1)-го порядка. Определитель

называется определителем Вронского для этой системы функций. Определитель Вронского вообще является функцией от , определенной в некотором интервале.

Пример 7. Найти определитель Вронского для функций .

Пример 8. Найти определитель Вронского для функций:

так как первая и последняя строки определителя пропорциональны.

Теорема. Если система функций линейно зависима на отрезке , то ее определитель Вронского тождественно равен нулю на этом отрезке.

Так, например, система функций линейно зависима в интервале , и определитель Вронского этих функций равен нулю всюду в этом интервале (см. примеры 4 и 8).

Эта теорема дает необходимое условие линейной зависимости системы функций. Обратное утверждение неверно, т. е. определитель Вронского может тождественно обращаться в ноль и в том случае, когда данные функции образуют линейно независимую систему на некотором интервале.

Пример 9. Рассмотрим две функции:

Графики их имеют вид, указанный на рис. 25.

Эта система функций линейно независима, так как тождество выполняется только при . В самом деле, рассматривая его на отрезке , мы получаем , откуда , так как ; на отрезке же имеем , откуда , так как на этом отрезке.

Найдем определитель Вронского системы. На отрезках и :

Таким образом, определитель Вронского на отрезке тождественно равен нулю.

Пусть имеем систему функций на отрезке . Положим

называется определителем Грама системы функций .

Теорема. Для того, чтобы система функций была линейно зависимой, необходимо и достаточно, чтобы ее определитель Грама равнялся нулю.

Пример 10. Показать, что функции и линейно зависимы на отрезке .

Вычислим определитель Грама следовательно, функции и линейно зависимы.

Видео:Линейная зависимость и линейная независимость. ТемаСкачать

Линейная зависимость системы векторов. Коллинеарные векторы

В данной статье мы расскажем:

что такое коллинеарные векторы;
какие существуют условия коллинеарности векторов;
какие существуют свойства коллинеарных векторов;
что такое линейная зависимость коллинеарных векторов.

Видео:Линейная зависимость и линейная независимость векторов.Скачать

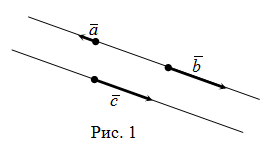
Коллинеарные векторы

Коллинеарные векторы — это векторы, которые являются параллелями одной прямой или лежат на одной прямой.

Видео:Линейная зависимость строк и определитель матрицыСкачать

Условия коллинеарности векторов

Два векторы являются коллинеарными, если выполняется любое из следующих условий:

условие 1. Векторы a и b коллинеарны при наличии такого числа λ , что a = λ b ;
условие 2. Векторы a и b коллинеарны при равном отношении координат:

a = ( a 1 ; a 2 ) , b = ( b 1 ; b 2 ) ⇒ a ∥ b ⇔ a 1 b 1 = a 2 b 2

условие 3. Векторы a и b коллинеарны при условии равенства векторного произведения и нулевого вектора:

Условие 2 неприменимо, если одна из координат вектора равна нулю.

Условие 3 применимо только к тем векторам, которые заданы в пространстве.

Видео:Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать

Примеры задач на исследование коллинеарности векторов

Исследуем векторы а = ( 1 ; 3 ) и b = ( 2 ; 1 ) на коллинеарность.

В данном случае необходимо воспользоваться 2-м условием коллинеарности. Для заданных векторов оно выглядит так:

Равенство неверное. Отсюда можно сделать вывод, что векторы a и b неколлинеарны.

Ответ: a | | b

Какое значение m вектора a = ( 1 ; 2 ) и b = ( — 1 ; m ) необходимо для коллинеарности векторов?

Используя второе условие коллинераности, векторы будут коллинеарными, если их координаты будут пропорциональными:

Отсюда видно, что m = — 2 .

Ответ: m = — 2 .

Видео:Линейная зависимость векторов на примерахСкачать

Критерии линейной зависимости и линейной независимости систем векторов

Система векторов векторного пространства линейно зависима только в том случае, когда один из векторов системы можно выразить через остальные векторы данной системы.

Пусть система e 1 , e 2 , . . . , e n является линейно зависимой. Запишем линейную комбинацию этой системы равную нулевому вектору:

a 1 e 1 + a 2 e 2 + . . . + a n e n = 0

в которой хотя бы один из коэффициентов комбинации не равен нулю.

Пусть a k ≠ 0 k ∈ 1 , 2 , . . . , n .

Делим обе части равенства на ненулевой коэффициент:

a k — 1 ( a k — 1 a 1 ) e 1 + ( a k — 1 a k ) e k + . . . + ( a k — 1 a n ) e n = 0

— a k — 1 a m , где m ∈ 1 , 2 , . . . , k — 1 , k + 1 , n

β 1 e 1 + . . . + β k — 1 e k — 1 + β k + 1 e k + 1 + . . . + β n e n = 0

или e k = ( — β 1 ) e 1 + . . . + ( — β k — 1 ) e k — 1 + ( — β k + 1 ) e k + 1 + . . . + ( — β n ) e n

Отсюда следует, что один из векторов системы выражается через все остальные векторы системы. Что и требовалось доказать (ч.т.д.).

Пусть один из векторов можно линейно выразить через все остальные векторы системы:

e k = γ 1 e 1 + . . . + γ k — 1 e k — 1 + γ k + 1 e k + 1 + . . . + γ n e n

Переносим вектор e k в правую часть этого равенства:

0 = γ 1 e 1 + . . . + γ k — 1 e k — 1 — e k + γ k + 1 e k + 1 + . . . + γ n e n

Поскольку коэффициент вектора e k равен — 1 ≠ 0 , у нас получается нетривиальное представление нуля системой векторов e 1 , e 2 , . . . , e n , а это, в свою очередь, означает, что данная система векторов линейно зависима. Что и требовалось доказать (ч.т.д.).

Система векторов является линейно независимой, когда ни один из ее векторов нельзя выразить через все остальные векторы системы.
Система векторов, которая содержит нулевой вектор или два равных вектора, линейно зависима.

Видео:Линейная зависимость векторов. РангСкачать

Свойства линейно зависимых векторов

Для 2-х и 3-х мерных векторов выполняется условие: два линейно зависимых вектора — коллинеарны. Два коллинеарных вектора — линейно зависимы.
Для 3-х мерных векторов выполняется условие: три линейно зависимые вектора — компланарны. (3 компланарных вектора — линейно зависимы).
Для n-мерных векторов выполняется условие: n + 1 вектор всегда линейно зависимы.

Видео:Линейная комбинация. Линейная зависимость (независимость) матриц.Скачать

Примеры решения задач на линейную зависимость или линейную независимость векторов

Проверим векторы a = 3 , 4 , 5 , b = — 3 , 0 , 5 , c = 4 , 4 , 4 , d = 3 , 4 , 0 на линейную независимость.

Решение. Векторы являются линейно зависимыми, поскольку размерность векторов меньше количества векторов.

Проверим векторы a = 1 , 1 , 1 , b = 1 , 2 , 0 , c = 0 , — 1 , 1 на линейную независимость.

Решение. Находим значения коэффициентов, при которых линейная комбинация будет равняться нулевому вектору:

x 1 a + x 2 b + x 3 c 1 = 0

Записываем векторное уравнение в виде линейного:

x 1 + x 2 = 0 x 1 + 2 x 2 — x 3 = 0 x 1 + x 3 = 0

Решаем эту систему при помощи метода Гаусса:

1 1 0 | 0 1 2 — 1 | 0 1 0 1 | 0

Из 2-ой строки вычитаем 1-ю, из 3-ей — 1-ю:

1 1 0 | 0 1 — 1 2 — 1 — 1 — 0 | 0 — 0 1 — 1 0 — 1 1 — 0 | 0 — 0

1 1 0 | 0 0 1 — 1 | 0 0 — 1 1 | 0

Из 1-й строки вычитаем 2-ю, к 3-ей прибавляем 2-ю:

1 — 0 1 — 1 0 — ( — 1 ) | 0 — 0 0 1 — 1 | 0 0 + 0 — 1 + 1 1 + ( — 1 ) | 0 + 0

0 1 0 | 1 0 1 — 1 | 0 0 0 0 | 0

Из решения следует, что у системы множество решений. Это значит, что существует ненулевая комбинация значения таких чисел x 1 , x 2 , x 3 , при которых линейная комбинация a , b , c равняется нулевому вектору. Следовательно, векторы a , b , c являются линейно зависимыми.