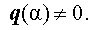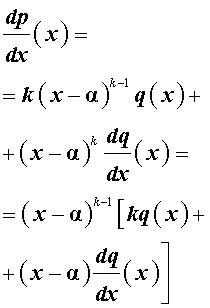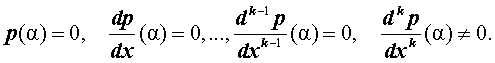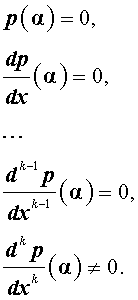Пусть p(x) – многочлен степени n , а q(x) – многочлен степени n – k , где n и k – натуральные числа, удовлетворяющие неравенству 
Определение . Число α называют корнем кратности k многочлена p(x) , если справедливо равенство
| p(x) = (x – α) k q (x) , | (1) |
Утверждение 1 . Число α является корнем кратности k многочлена p(x) тогда и тогда, когда оно является корнем производной этого многочлена кратности k – 1 .
Доказательство . Взяв производную от обеих частей формулы (1), получаем
Поскольку выражение, стоящее в квадратных скобках, при x = α не обращается в нуль, то утверждение 1 доказано.
Из утверждения 1 вытекает следующее
Утверждение 2 . Число α является корнем кратности k многочлена p(x) тогда и тогда, когда выполнены равенства:
Задача . Найти все значения параметра m , при которых многочлен
имеет корень кратности 2 .
Решение . Воспользовавшись утверждением 2, получаем
Видео:ЛЕКЦИЯ 4.3: Математическое отступление: понятие кратности корня многочленаСкачать

Кратные корни многочлена
При рассмотрении вопроса о корнях многочлена, особо выделяют понятие кратных корней.
Определение. Пусть задан многочлен $fleft(xright) in Pleft[xright]$ ($Pleft[xright]$ — множество всех многочленов от буквы $x$ над полем $P$) и $alpha$, где $alpha$ — корень многочлена $fleft(xright)$. Элемент $alpha$ назовем $k$-кратным ($k in mathbb $, $k>1$) корнем многочлена, если имеет место следующее представление: $$fleft(xright)=left(x-alpharight)^k f_left(xright),, f_left(alpharight) ne 0.$$
Принято рассматривать понятие кратного корня для $k>1$. Если же $fleft(xright)$ можно представить следующим образом: $$fleft(xright)=left(x-alpharight) f_left(xright),, f_left(alpharight) ne 0,$$ то $alpha$ называется простым (однократным) корнем многочлена$fleft(xright)$. Если для $fleft(xright)$ имеет место следующее равенство: $$fleft(xright)=left(x-alpharight)^2 f_left(xright),, f_left(alpharight) ne 0,$$ то $alpha$ называется двукратным корнем многочлена $fleft(xright)$. Аналогично, существуют корни трехкратные, четырехкратные и так далее.
Часто условие $f_left(alpharight) ne 0$ заменяют на $f_left(xright),barvdots,(x-alpha)$. Эквивалентность этих условий вытекает из следствий теоремы Безу. Тогда, набор условий, что $f(x),vdots,left(x-alpharight)^k$, но $f(x),barvdots,left(x-alpharight)^$ эквивалентен тому, что $alpha$ — $k$-кратный корень многочлена $f(x)$.
Видео:кратные корниСкачать

Процесс нахождения кратности корня
Пусть задан многочлен $fleft(xright) in Pleft[xright]$ и его корень $alpha$ ( $deg fleft(xright) > 0$). Рассмотрим задачу о нахождении кратности корня $alpha$.
Так как $alpha$ — корень $fleft(xright)$, то имеет место следующее представление: $$fleft(xright)=left(x-alpharight)f_left(xright).$$ Тогда, если $alpha$ не является корнем $f_left(xright)$ ($f_left(alpharight) ne 0$), то, по определению, $alpha$ — простой корень многочлена $fleft(xright)$. В противном случае, $alpha$ — $k$-кратный ($k in mathbb $, $k > 1 $) корень $fleft(xright)$. Задача сводится к нахождению $k-1$, то есть к нахождению кратности корня $f_left(xright)$, где $deg f_left(xright) = deg fleft(xright) — 1$. Учитывая, что $deg fleft(xright) > 0$, то повторение такого алгоритма решает задачу. Для этого используется алгоритм Горнера.
Стоит упомянуть, что иногда удобней пользоваться критерием кратности корня.
Видео:Схема Горнера. 10 класс.Скачать

Примеры решения задач
- Пусть задан многочлен $fleft(xright)=x^3-3x^2+4$. Определить, является ли $2$ корнем многочлена $f(x)$. В случае положительного ответа найти его кратность.
Для решении задачи воспользуемся алгоритмом Горнера. Стоит обратить внимание на то, что хоть и слагаемое вида $a_x^1$ отсутствует в записи, но нулевой коэффициент необходимо не забыть занести в таблицу.
| $1$ | $-3$ | $0$ | $4$ | |
| $2$ | $1$ | $-1$ | $-2$ | $0$ |
| $2$ | $1$ | $1$ | $0$ | |
| $2$ | $1$ | $3$ |
Из таблицы видно, что многочлен $f(x)$ поделился на $left(x-2right)^2$ без остатка, а на $left(x-2right)^3$ — нет. Получаем, что $2$ — двукратный корень многочлена $f(x)$.
Так как $alpha$ — двукратный корень многочлена $f(x)$, то $f(x)$ представим в следующем виде: $$fleft(xright)=left(x-alpharight)^2 f_left(xright),$$где $f_(alpha) ne 0$. Аналогично, $g(x)$ можно представить следующим образом: $$gleft(xright)=left(x-alpharight) g_left(xright),$$где $g_(alpha) ne 0$. Тогда, $$f(x)g(x)=left(x-alpharight)^2f_(x)(x-alpha)g_(x)=left(x-alpharight)^3f_(x)g_(x).$$Так как $f_(alpha) ne 0$ и $g_(alpha) ne 0$, то $f_(alpha)g_(alpha)ne0$. Обозначим $f(x)g(x)=h(x)$, $f_(x)g_(x)=h_(x)$, тогда перепишем выражение многочлена $f(x)g(x)$ следующим образом: $$h(x)=left(x-alpharight)^3h_(x),$$ где $h_(alpha)ne0$. Тогда по определению $alpha$ — корень $f(x)g(x)$ третьей кратности.
Для решении задачи воспользуемся алгоритмом Горнера.
| $1$ | $5$ | $10$ | $10$ | $5$ | $1$ | |
| $-1$ | $1$ | $4$ | $6$ | $4$ | $1$ | $0$ |
| $-1$ | $1$ | $3$ | $3$ | $1$ | $0$ | |
| $-1$ | $1$ | $2$ | $1$ | $0$ | ||
| $-1$ | $1$ | $1$ | $0$ | |||
| $-1$ | $1$ | $0$ |
Из таблицы видно, что многочлен пятой степени $f(x)$ поделился на $left(x+1right)^5$ без остатка. Получаем, что $-1$ — корень пятой кратности.
По определению, для того, что бы $2$ была корнем второй кратности, необходимо что бы имело место следующее представление: $$f(x)=left(x-2right)^2f_(x),, f_(2) ne 0.$$С другой стороны, в нашем случае: $$f_(x)=x^2+x-6=(x-2)(x+3),, f_(2)=0.$$ Получаем, что $2$ не корень второй кратности. Тогда найдем его кратность. Выразим $f(x)$ подставив $f_(x)=(x-2)(x+3)$:$$f(x)=left(x-2right)^3(x+3)=left(x-2right)^3f_(x),$$ $f_(2)=(2+3)=5ne0$. Значит, по определению, $2$ — корень многочлена $f(x)$ третьей кратности.
Представим исходный многочлен следующим образом: $$f(x)=x^4(x^4-8x^3+10x^2-1).$$
Обозначим $f_(x)=x^4-8x^3+10x^2-1$. Легко убедиться, что $f_(0)=-1ne0$. Получаем, что, по определению кратного корня, $0$ — корень многочлена $f(x)$ четвертой кратности.
Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

научная статья по теме ОПРЕДЕЛЕНИЕ КРАТНОСТИ КОРНЯ НЕЛИНЕЙНОГО АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ Математика
Цена:
Авторы работы:
Научный журнал:
Год выхода:
Видео:СЛОЖИТЕ ДВА КОРНЯСкачать

Текст научной статьи на тему «ОПРЕДЕЛЕНИЕ КРАТНОСТИ КОРНЯ НЕЛИНЕЙНОГО АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ»
ЖУРНАЛ ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКИ И МАТЕМАТИЧЕСКОЙ ФИЗИКИ, 2008, том 48, 2) — линейно. По скорости сходимости можно определить кратность корня.
Очевидно, что (р — 1)/р = A. + 1/Ai + O(As). Величины As, As + 1 нам не известны, поскольку в них входит неизвестное значение x*. Однако нетрудно показать, что таким же (с точностью до малых величин) будет отношение (xs + 1 — xs)/(xs — xs _ 1). Удобно ввести знаменатель линейной сходимости по формуле
📸 Видео
Математика без Ху!ни. Деление многочлена на многочлен.Скачать

Рациональные корни многочлена с целым показателем. 10 класс.Скачать

Теорема Безу и разложение многочлена на множителиСкачать

Жесть на ЕГЭ #3 КОРЕНЬ ЧЁТНОЙ КРАТНОСТИ | КВАДРАТИК?Скачать

4 Кратные корни. Теорема Безу. Наибольший общий делитель многочлена и его производнойСкачать

Теорема Безу, схема Горнера и корни многочленаСкачать

О кратности корней в методе интерваловСкачать

Математика 5 класс. Уравнение. Корень уравненияСкачать

Число корней уравнения в кольце. Теорема РушеСкачать

ЕГЭ по математике. Профильный уровень. Задание 5. Найдите корень уравненияСкачать

Кратность корня - как она выглядит на графике?Скачать

🔴 Найдите корень уравнения 2+9x=4x+3 | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 7 | ШКОЛА ПИФАГОРАСкачать

§49.2 Корни многочленаСкачать

Математика без Ху!ни. Комплексные числа, часть 4. Извлечение корня n-й степени.Скачать

ЧТО ТАКОЕ КОРЕНЬ В N- СТЕПЕНИ? Пригодится для ЕГЭ #shorts #егэ #огэ #математика #корни #mathСкачать