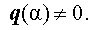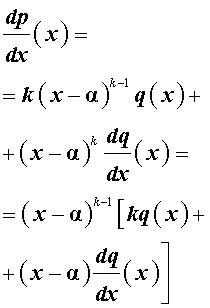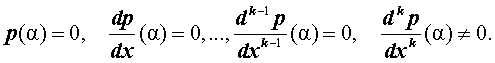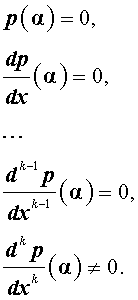Как определить кратность корня для уравнения (5 видео)

Кратные корни многочленов

Пусть p(x) – многочлен степени n , а q(x) – многочлен степени n – k , где n и k – натуральные числа, удовлетворяющие неравенству .

Определение . Число α называют корнем кратности k многочлена p(x) , если справедливо равенство

p(x) = (x – α) k q (x) ,

(1)

Утверждение 1 . Число α является корнем кратности k многочлена p(x) тогда и тогда, когда оно является корнем производной этого многочлена кратности k – 1 .

Доказательство . Взяв производную от обеих частей формулы (1), получаем

Поскольку выражение, стоящее в квадратных скобках, при x = α не обращается в нуль, то утверждение 1 доказано.

Из утверждения 1 вытекает следующее

Утверждение 2 . Число α является корнем кратности k многочлена p(x) тогда и тогда, когда выполнены равенства:

Задача . Найти все значения параметра m , при которых многочлен

имеет корень кратности 2 .

Решение . Воспользовавшись утверждением 2, получаем

Содержание

Кратные корни многочлена
Процесс нахождения кратности корня
Примеры решения задач
Как определить кратность корня для уравнения
Разделы
Дополнительно
🔍 Видео

Видео:ЛЕКЦИЯ 4.3: Математическое отступление: понятие кратности корня многочленаСкачать

Кратные корни многочлена

При рассмотрении вопроса о корнях многочлена, особо выделяют понятие кратных корней.

Определение. Пусть задан многочлен $fleft(xright) in Pleft[xright]$ ($Pleft[xright]$ — множество всех многочленов от буквы $x$ над полем $P$) и $alpha$, где $alpha$ — корень многочлена $fleft(xright)$. Элемент $alpha$ назовем $k$-кратным ($k in mathbb $, $k>1$) корнем многочлена, если имеет место следующее представление: $$fleft(xright)=left(x-alpharight)^k f_left(xright),, f_left(alpharight) ne 0.$$

Принято рассматривать понятие кратного корня для $k>1$. Если же $fleft(xright)$ можно представить следующим образом: $$fleft(xright)=left(x-alpharight) f_left(xright),, f_left(alpharight) ne 0,$$ то $alpha$ называется простым (однократным) корнем многочлена$fleft(xright)$. Если для $fleft(xright)$ имеет место следующее равенство: $$fleft(xright)=left(x-alpharight)^2 f_left(xright),, f_left(alpharight) ne 0,$$ то $alpha$ называется двукратным корнем многочлена $fleft(xright)$. Аналогично, существуют корни трехкратные, четырехкратные и так далее.

Часто условие $f_left(alpharight) ne 0$ заменяют на $f_left(xright),barvdots,(x-alpha)$. Эквивалентность этих условий вытекает из следствий теоремы Безу. Тогда, набор условий, что $f(x),vdots,left(x-alpharight)^k$, но $f(x),barvdots,left(x-alpharight)^$ эквивалентен тому, что $alpha$ — $k$-кратный корень многочлена $f(x)$.

Видео:кратные корниСкачать

Процесс нахождения кратности корня

Пусть задан многочлен $fleft(xright) in Pleft[xright]$ и его корень $alpha$ ( $deg fleft(xright) > 0$). Рассмотрим задачу о нахождении кратности корня $alpha$.

Так как $alpha$ — корень $fleft(xright)$, то имеет место следующее представление: $$fleft(xright)=left(x-alpharight)f_left(xright).$$ Тогда, если $alpha$ не является корнем $f_left(xright)$ ($f_left(alpharight) ne 0$), то, по определению, $alpha$ — простой корень многочлена $fleft(xright)$. В противном случае, $alpha$ — $k$-кратный ($k in mathbb $, $k > 1 $) корень $fleft(xright)$. Задача сводится к нахождению $k-1$, то есть к нахождению кратности корня $f_left(xright)$, где $deg f_left(xright) = deg fleft(xright) — 1$. Учитывая, что $deg fleft(xright) > 0$, то повторение такого алгоритма решает задачу. Для этого используется алгоритм Горнера.

Стоит упомянуть, что иногда удобней пользоваться критерием кратности корня.

Видео:Схема Горнера. 10 класс.Скачать

Примеры решения задач

Пусть задан многочлен $fleft(xright)=x^3-3x^2+4$. Определить, является ли $2$ корнем многочлена $f(x)$. В случае положительного ответа найти его кратность.

Для решении задачи воспользуемся алгоритмом Горнера. Стоит обратить внимание на то, что хоть и слагаемое вида $a_x^1$ отсутствует в записи, но нулевой коэффициент необходимо не забыть занести в таблицу.

$1$	$-3$	$0$	$4$
$2$	$1$	$-1$	$-2$	$0$
$2$	$1$	$1$	$0$
$2$	$1$	$3$

Из таблицы видно, что многочлен $f(x)$ поделился на $left(x-2right)^2$ без остатка, а на $left(x-2right)^3$ — нет. Получаем, что $2$ — двукратный корень многочлена $f(x)$.

Так как $alpha$ — двукратный корень многочлена $f(x)$, то $f(x)$ представим в следующем виде: $$fleft(xright)=left(x-alpharight)^2 f_left(xright),$$где $f_(alpha) ne 0$. Аналогично, $g(x)$ можно представить следующим образом: $$gleft(xright)=left(x-alpharight) g_left(xright),$$где $g_(alpha) ne 0$. Тогда, $$f(x)g(x)=left(x-alpharight)^2f_(x)(x-alpha)g_(x)=left(x-alpharight)^3f_(x)g_(x).$$Так как $f_(alpha) ne 0$ и $g_(alpha) ne 0$, то $f_(alpha)g_(alpha)ne0$. Обозначим $f(x)g(x)=h(x)$, $f_(x)g_(x)=h_(x)$, тогда перепишем выражение многочлена $f(x)g(x)$ следующим образом: $$h(x)=left(x-alpharight)^3h_(x),$$ где $h_(alpha)ne0$. Тогда по определению $alpha$ — корень $f(x)g(x)$ третьей кратности.

Для решении задачи воспользуемся алгоритмом Горнера.

$1$	$5$	$10$	$10$	$5$	$1$
$-1$	$1$	$4$	$6$	$4$	$1$	$0$
$-1$	$1$	$3$	$3$	$1$	$0$
$-1$	$1$	$2$	$1$	$0$
$-1$	$1$	$1$	$0$
$-1$	$1$	$0$

Из таблицы видно, что многочлен пятой степени $f(x)$ поделился на $left(x+1right)^5$ без остатка. Получаем, что $-1$ — корень пятой кратности.

По определению, для того, что бы $2$ была корнем второй кратности, необходимо что бы имело место следующее представление: $$f(x)=left(x-2right)^2f_(x),, f_(2) ne 0.$$С другой стороны, в нашем случае: $$f_(x)=x^2+x-6=(x-2)(x+3),, f_(2)=0.$$ Получаем, что $2$ не корень второй кратности. Тогда найдем его кратность. Выразим $f(x)$ подставив $f_(x)=(x-2)(x+3)$:$$f(x)=left(x-2right)^3(x+3)=left(x-2right)^3f_(x),$$ $f_(2)=(2+3)=5ne0$. Значит, по определению, $2$ — корень многочлена $f(x)$ третьей кратности.

Представим исходный многочлен следующим образом: $$f(x)=x^4(x^4-8x^3+10x^2-1).$$
Обозначим $f_(x)=x^4-8x^3+10x^2-1$. Легко убедиться, что $f_(0)=-1ne0$. Получаем, что, по определению кратного корня, $0$ — корень многочлена $f(x)$ четвертой кратности.

Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

Как определить кратность корня для уравнения

Видео:Рациональные корни многочлена с целым показателем. 10 класс.Скачать

Разделы

Видео:СЛОЖИТЕ ДВА КОРНЯСкачать

Дополнительно

Алгебраическим уравнением степени $n$ с одной неизвестной $x$ называется уравнение вида

$P_n(x) = a_0 x^n + a_1 x^ + cdots + a_n = 0 (a_0 neq 0)$ (1)

(т. е. уравнение $f(x) = 0$, в левой части которого стоит ц. р. ф степени $n$ от $х$).

Для алгебраических уравнений принято ставить задачу отыскания всех (вообще говоря, комплексных) корней уравнения. Так как корнями уравнения (1) являются нули (корни) многочлена в его левой части, то можно использовать сведения о целых рациональных функциях и их корнях. Утверждение формулируются применительно к уравнению (1) следующим образом:

1) Каждое уравнение степени $n$ имеет по меньшей мере один корень в комплексной области. Если каждый корень учитывать с его кратностью, т. е. считать за столько корней, какова его кратность, то число корней уравнения равно его степени $n$. При этом говорят, что $x = alpha$ — корень кратности $k$, если левая часть уравнения делится на $(x — alpha)^k$ нацело, но не делится нацело на $(x — alpha)^$.

2) Если уравнение (1) имеет комплексный (мнимый) корень $x = sigma + i tau$, то и комплексно сопряженное число $bar = sigma — i tau$ является корнем уравнения (кратности обоих сопряженных корней одинаковы).

На протяжении столетий главной задачей алгебры было указание правил решения алгебраических уравнений. С древности известны формулы для решения уравнений первой и второй степени. Итальянскими математиками эпохи Возрождения (Кардано, Тарталья, Феррари) были найдены формулы для решения уравнений третьей и четвертой степени (они громоздки и не имеют большого практического значения). Попытки решения «в радикалах» (т. е. с применением действия извлечения корня) уравнений степени выше четвертой были в общем случае безуспешны. Уже в XIX веке в работах Руффини, Абеля и Галуа было установлено, что не только для корней общего уравнения степени выше четвертой не может быть дано формул, выражающих их в радикалах, но и что корни многих конкретных уравнений с числовыми (например, целыми) коэффициентами не могут быть выражены через радикалы из рациональных чисел.