Замечание.Также в случае, когда правая часть уравнения имеет вид
и, 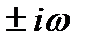
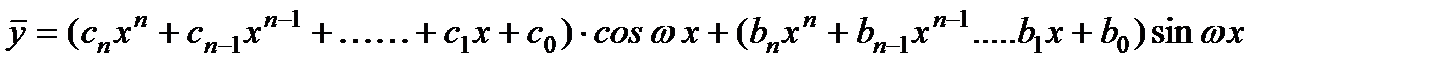
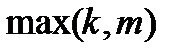
В том случае 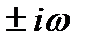
ЗАДАЧИ
1) Для заданных дифференциальных уравнений выписать характеристические уравнения и базисные решения (фундаментальную систему решений), записать общее решение однородного уравнения, 2) для неоднородных уравнений найти частное решение методом неопределенных коэффициентов (комплексных амплитуд), записать решение неоднородного уравнения, 3) при заданных начальных условиях найдите частное решение.
1) 
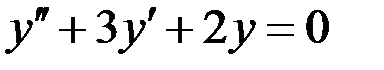
4) 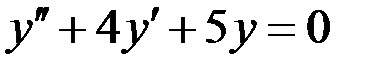
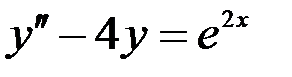
7) 
9) 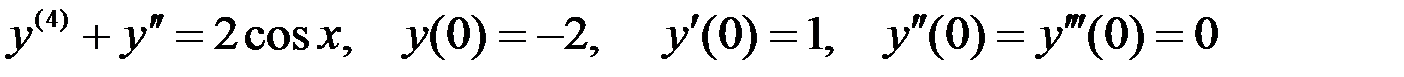
10.) 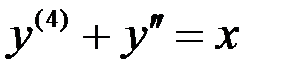
11).
Ответы : 9)
11)
12). Для уравнения затухающихколебаний
( x -координата, 

Для уравнения вынужденных колебаний
найдите частное решение методом комплексных амплитуд при условии, что 


Контрольные вопросы
1. Что является решением дифференциального уравнения?
Дайте определение общего и частного решений дифференциального уравнения
2. Сформулируйте теорему существования и единственности для дифференциального уравнения первого порядка
3. Определите тип дифференциального уравнения:
4. Решением дифференциального уравнения 
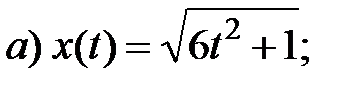
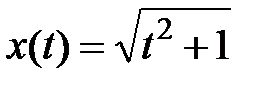
5. Дифференциальное уравнение семейства кривых 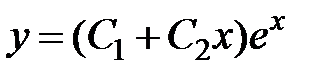
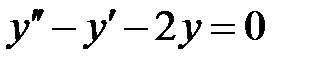
6. Частное решение дифференциального уравнения 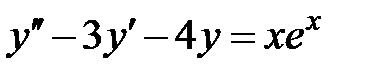
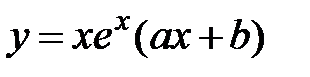
7. Корни характеристического 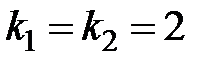
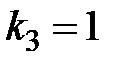
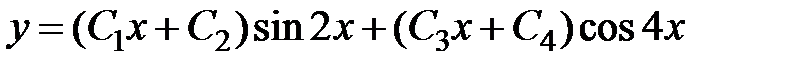
8. Среди перечисленных дифференциальных уравнений уравнениями первого порядка являются:
Варианты ответов:
Должен быть указан не менее двух вариантов ответа
9. Из данных дифференциальных уравнений уравнениями c разделяющимися переменными являются…
Варианты ответов:
Должен быть указан не менее двух вариантов ответа
10. Дано дифференциальное уравнение 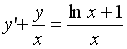
11. Общий интеграл дифференциального уравнения 
12. Общее решение дифференциального уравнения 
13. Решением уравнения первого порядка 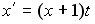
14. Общее решение дифференциального уравнения 
15. Общее решение дифференциального уравнения 
16. Общее решение дифференциального уравнения 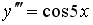
17. Общее решение дифференциального уравнения 
18. Общее решение дифференциального уравнения 
19. Общее решение линейного однородного дифференциального уравнения второго порядка 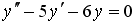
20. Однородному дифференциальному уравнению второго порядка 
21. Дано линейное однородное дифференциальное уравнение 
22. Дано дифференциальное уравнение 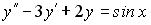
23. Методы приближенного решения дифференциальных уравнений.
РГР № 14 (0,600 ЗЕ)
Функции комплексной переменной
Срок выполнения 9- 13 недели
Содержание работы
1. Комплексные числа. Алгебраическая, тригонометрическая, показательная форма записи. Действия с комплексными числами
2. Функции комплексной переменной. Аналитические функции
3. Вычет аналитической функции в изолированной особой точке. Вычисление контурных и несобственных интегралов при помощи вычетов.
4. Ряды и преобразования Фурье.
5. Преобразования Лапласа.
6. Решение линейных дифференциальных уравнений и систем уравнений операторным методом.
7. Решение линейных дифференциальных уравнений методом свертки (формулы Дюамеля, Грина).
Литература [2, 3, 4, 11,16, 19]
1. Комплексные числа На множестве действительных чисел не существует такого числа, которое являлось бы корнем простейшего алгебраического уравнения 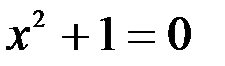 (поскольку квадрат любого действительного числа неотрицателен). Поэтому возникла потребность расширить множество действительных чисел таким образом, чтобы новое множество содержало корни всех алгебраических уравнений. Введение комплексных чисел позволяет достигнуть этой цели. Прежде всего введем новый символ – (поскольку квадрат любого действительного числа неотрицателен). Поэтому возникла потребность расширить множество действительных чисел таким образом, чтобы новое множество содержало корни всех алгебраических уравнений. Введение комплексных чисел позволяет достигнуть этой цели. Прежде всего введем новый символ – 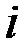 , который называют мнимой единицей таким образом, что , который называют мнимой единицей таким образом, что  . Тогда корни уравнения . Тогда корни уравнения 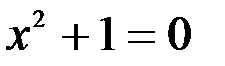 запишутся как запишутся как 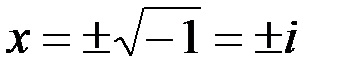 . Алгебраическая форма записи комплексного числа Комплексное число в алгебраической форме записывается как . Алгебраическая форма записи комплексного числа Комплексное число в алгебраической форме записывается как 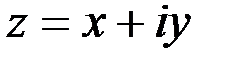 . Здесь . Здесь  – действительное число, называемое реальной или действительной частью комплексного числа. Обозначают: – действительное число, называемое реальной или действительной частью комплексного числа. Обозначают: 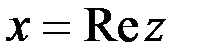 . Действительное число . Действительное число  называют мнимой частью комплексного числа. Обозначают: называют мнимой частью комплексного числа. Обозначают: 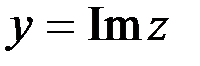 . Таким образом, комплексное число – это упорядоченная пара действительных чисел . Таким образом, комплексное число – это упорядоченная пара действительных чисел 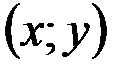 . Если . Если 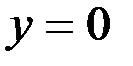 , то комплексное число совпадает с действительным и изображается точкой на действительной оси ОХ. При , то комплексное число совпадает с действительным и изображается точкой на действительной оси ОХ. При  получаются чисто мнимые числа получаются чисто мнимые числа 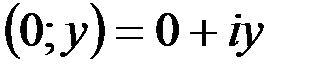 , которые изображаются точкой на мнимой оси OY. Комплексное число , которые изображаются точкой на мнимой оси OY. Комплексное число 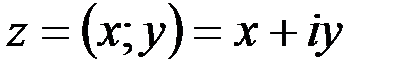 можно отождествить с точкой плоскости OXY или радиусом – вектором можно отождествить с точкой плоскости OXY или радиусом – вектором  . Плоскость OXY будем называть комплексной плоскостью (рис. 1) Два комплексных числа равны, если равны их действительные и мнимые части: . Плоскость OXY будем называть комплексной плоскостью (рис. 1) Два комплексных числа равны, если равны их действительные и мнимые части: 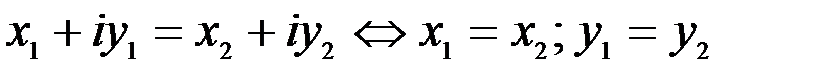 . Два комплексных числа называют сопряженными, если действительные части этих чисел равны, а мнимые отличаются знаком. Обозначают: . Два комплексных числа называют сопряженными, если действительные части этих чисел равны, а мнимые отличаются знаком. Обозначают: 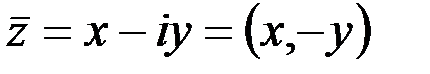 . Над комплексными числами в алгебраической форме определены следующие операции: . Над комплексными числами в алгебраической форме определены следующие операции: Сумма Разность Особо отметим произведение комплексно-сопряженных чисел, которое является числом действительным: Пример 1. Найти значение функции Второе слагаемое есть частное от деления двух комплексных чисел. Используя правило деления комплексных чисел в алгебраической форме, получим: Итак, Пример 2. Решить уравнение По формуле для корней квадратного уравнения имеем: Извлекая корень квадратный из числа Содержание Видео:13. Как решить дифференциальное уравнение первого порядка?Скачать  Линейные однородные дифференциальные уравнения с постоянными коэффициентамиСодержание: По этой ссылке вы найдёте полный курс лекций по математике: Частный случай: уравнение второго порядка Пусть имеем линейное однородное дифференциальное уравнение второго порядка где р, Р2 — действительные числа. Чтобы найти общее решение этого уравнения, надо найти два его линейно независимых частных решения. Следуя Эйлеру, будем искать их в виде где тогда Подставляя эти выражения для у и ее производных в уравнение (1), получаем . Так как , то должно выполняться равенство Следовательно, функция у = eAz будет решением уравнения (1), т. е. будет обращать его в тождество по х, если А будет удовлетворять алгебраическому уравнению Уравнение (3) называется характеристическим уравнением по отношению к уравнению (1), а его левая часть называется характеристическим много-членом. Уравнение (3) есть квадратное уравнение. Обозначим его корни через А] и 1 они могут быть 1) действительными и разными; 2) комплексными; 3) действительными и равными. Рассмотрим каждый случай в отдельности. 1. Если корни Л|, Аг характеристического уравнения действительные и разные, то частными решениями уравнения (1) будут функции Эти решения линейно независимы (Aj Ф А2) и, следовательно, образуют фундаментальную систему решений уравнения. Общее решение уравненияОбщее решение уравнения имеет вид — произвольные постоянные). Пример 1. Найти общее решение уравнения М Составляем характеристическое уравнение: Оно имеет корни Линейные однородные дифференциальные уравнения с постоянными коэффициентами Общий случай: уравнение произвольного порядка Физические приложения: уравнение колебаний Уравнения, приводящие к уравнениям с постоянными коэффициентами Линейные неоднородные дифференциальные уравнения Отсюда получаем искомое общее решение 2. Пусть корни характеристического уравнения комплексные. Так как коэффициенты р], р2 характеристического уравнения действительные, комплексные корни входят попарно сопряженными. Положим, что Частные решения дифференциального уравнения (1) можно записать в виде Это комплекснозначные функции действительного аргумента х, а мы будем заниматься лишь действительными решениями. С помощью формул Эйлера частные решения ij и у2 уравнения (1) можно представить в виде Воспользовавшисьтеоремой 4, получим, что частными решениями уравнения (1) будут также функции _ Эти решения линейно независимы, так как Решения образуют фундаментальную систему решений уравне-ния (1), общее решение которого в этом случае имеет вид или Пример 3. Найти общее решение уравнения 4 Характеристическое уравнение имеет кратные корни Поэтому общее решение исходного дифференциального уравнения: Замечание. Пусть имеем линейное однородное дифференциальное уравнение (вообще, с переменными коэффициентами) Пусть — частное решение уравнения. Введем новую искомую функцию ti(x) соотношением (разрешимым относительно н(х) в тех интервалах, где yi(x) не обращается в нуль). Из этого соотношения найдем производные от у : и подставим их в уравнение (5): Для функции и(х) получаем опять уравнение порядка п, но коэффициент при м(х) есть £(yil-Он тождественно равен нулю, так как yi (х) есть решение уравнения (5). Следовательно, в полученном уравнении порядок понизится, если ввести новую искомую функцию z(x) = и'(х). Разделив, кроме того, все члены последнего уравнения на yi(x) Ф 0, приведем его к виду Итак, если известно частное решение уравнения (5), то задача интегрирования этого уравнения приводится к интегрированию линейного однородного уравнения порядка п — . Можно показать, что если известны два частных линейно независимых решения, то порядок уравнения может быть понижен на две единицы. Вообше, если известно г частных линейно независимых решений линейного однородного дифференциального уравнения, то порядок этого уравнения может быть понижен на г единиц. 6.2. Физические приложения: уравнение колебаний Линейные дифференциальные уравнения с постоянными коэффициентами возникают в задачах о механических и электрических колебаниях. Рассмотрим уравнение свободных механических колебаний, причем независимой переменной будем считать время t: где у — отклонение колеблющейся точки от положения равновесия, rh — масса точки, h — коэффициент трения (считаем, что сила трения пропорциональна скорости), к > 0 — коэффициент упругости восстанавливающей силы (считаем, что эта сила пропорциональна отклонению). Характеристическое уравнениеХарактеристическое уравнение для (6) имеет корни Если трение достаточно велико, h2 > Атк, то эти корни действительные и отрицательные. Общее решение уравнения (6) в этом случае имеет вид Так как то из (7) заключаем, что при большом трен и и отклонение точки от положения равновесия с возрастанием t стремится к нулю, не совершая колебаний. Если трение мало, Атк, то характеристическое уравнение имеет комплексно сопряженные корни Общее решение уравнения (6) в этом случае определяется формулой или Отсюда видно, что в случае малого трения происходят затухающие колебания. Пусть теперь трение отсутствует, . В этом случае характеристическое уравнение имеет чисто мнимые корни Решение уравне- ния (6) имеет вид . в этом случае происходят незатухающие гармонические колебания с частотой ш = и произвольными амплитудой А и начальной фазой 6. Задача. При каких 1) все решения уравнения стремятся к нулю при 2) каждое решение уравнения обращается в нуль на бесконечном множестве точек х? 6.3. Общий случай: уравнение произвольного порядка Рассмотрим теперь линейное однородное дифференциальное уравнение произвольного порядка п (п ^ 1) с постоянными коэффициентами ) гдерьрг,,Рп — действительные числа. Общее решение дифференциального уравнения (8) находим так же, как и в случае уравнения второго порядка. Ищем решение в виде Подставляя вместо у величину еХх в уравнение (8), получаем , что приводит к характеристическому уравнению 2. Находим корни характеристического уравнения. 3. По характеру корней выписываем частные линейно независимые решения уравнения (8), руководствуясь тем, что: а) Каждому действительному однократному корню А характеристическою уравнения соответствует частное решение уравнения (8). б) Каждой паре однократных комплексно сопряженных корней соответствуют два линейно независимых частных решения уравнения (8). в) Каждому действительному корню А кратности г соответствует г линейно независимых частных решений уравнения (8). Рассмотрим случай в) подробнее. Пусть число А есть корень кратности г характеристического уравнения . Функцию будем рассматривать как функцию двух аргументов: ж и А. Возможно вам будут полезны данные страницы: Она имеет непрерывные производные по а: и по А всех порядков, причем Поэтому частные производные функции по х и по А не зависят от порядка дифференцирования (операции дифференцирования функции у по х и по А перестановочны), так что Воспользовавшись этой перестановочностью, а также тем, что Если А есть г-кратный корень характеристического уравнения то стало быть, правые части (10) и (11) тождественно по х равны нулю: Это означает, что функции являются в этом случае решениями уравнения (8).
Поэтому каждой паре комплексно сопряженных корней p кратности l отвечает 2/х частных решений уравнения 4. Число построенных таким образом частных решений уравнения (8) равно порядку п этого уравнения. Можно показать, что все эти решения линейно независимы в совокупности. Имея п линейно независимых частных решений 3/i(x), skfc). уп(я) уравнения (8), получаем общее решение этого уравнения, где произвольные постоянные. Прммер 4. Найти общее решение уравнения Составляем характеристическое уравнение: 2. Находим корни характеристического уравнения: 3. По характеру корней выписываем частные линейно независимые решения дифференциального уравнения: 4. Общее решение дифференциального уравнения имеет вид Схема решения линейного дифференциального уравнения с постоянными коэффициентами Дифференциальное уравнение действительные числа). Характеристическое уравнение Корни характеристического уравнения Частные линейно независимые решения дифференциального уравнения Общее решение уравнения — произвольные постоянные). §7. Уравнения, приводящие к уравнениям с постоянными коэффициентами Существуют линейные дифференциальные уравнения с переменными коэффициентами, которые с помощью замены переменных преобразуются в уравнения с постоянными коэффициентами. К их числу принадлежит уравнение Эйлера где pi.tp2, —tPn — постоянные числа. Ограничимся рассмотрением уравнения Эйлера 2-го порядка (оно встречается в задачах математической физики): Линейные однородные дифференциальные уравнения с постоянными коэффициентами Общий случай: уравнение произвольного порядка Физические приложения: уравнение колебаний Уравнения, приводящие к уравнениям с постоянными коэффициентами Линейные неоднородные дифференциальные уравнения Положим Подставляя выражения для , получим дифференциальное уравнение с постоянными коэффициентами. Последнее интегрируется обычным приемом: составляем характеристическое уравнение находим его корни и по характеру корней выписываем общее решение уравнения (2), после чего возвращаемся к старой переменной х. Пример. Найти общее решение уравнения Замена переменной х = приводит к уравнению характеристическое уравнение которого имеет корни Общее решение преобразованного уравнения равно Учитывая, что , для общего решения исходного уравнения получаем выражение Замечание 1. Для преобразованного уравнения (2) в случае действительных и различных корней характеристического уравнения (3) частные решения имеют вид Поэтому можно сразу задаться этим видом частного решения. Подставляя в уравнение (1), получим для к уравнение ) совпадающее с (3). Каждому простому действительному корню уравнения (4) отвечает частное решение уравнения (1); двукратному корню отвечают два решения уравнения (1). Паре комплексных сопряженных корней уравнения (4) будут соответствовать два решения уравнения (I). Замечание 2. Уравнение постоянные числа) подстановкой также приводится к уравнению с постоянными коэффициентами. §8. Линейные неоднородные дифференциальные уравнения Линейное неоднородное дифференциальное уравнение п-го порядка имеет вид Здесь заданные на некотором интервале (а, р) функции. Если ао(ж) Ф 0 на (а, то после деления на ац(х) получим уравнение. Из теоремы 1 существования и единственности решения задачи Коши получаем: если на отрезке [а, 6] коэффициенты Рк(х) и правая часть /(х) уравнения (2) непрерывны, то это уравнение имеет единственное решение, удовлетворяющее условиям Уравнение (2) можно записать в виде где, как и выше, Теорема 12. Если у(х) есть решение неоднородного уравнения есть решение соответствующего однородного уравнения мПо условию, В силу линейности оператора £ имеем Это означает, что функция есть решение уравнения Теорема 13. Если у(х) есть решение уравнения есть решение уравнения та функция есть решение уравнения По условию, используя линейность оператора £, получаем Последнее означает, что функция есть решение уравнения Теорема выражает так называемый принцип суперпозиции (наложения). Теорема 14. Если уравнение где все коэффициенты и функции действительные, имеет решение то действительная часть решения и(х) и его мнимая часть v(x) являются соответственно решениями уравнений. По условию имеем Отсюда получаем: Теорема 15 (о структуре общего решения линейного неоднородного дифференциального уравнения). Общее решение в области — уравнения с непрерывными на отрезке коэффициентами , и правой частью f(x) равно сумме общего решения соответствующего однородного уравнения и какого-нибудь частного решения у(х) неоднородного уравнения, т. е. Надо доказать, что где произвольные постоянные, линейно независимые решения соответствующего однородного уравнения £[у] = 0, является общим решением неоднородного уравнения. Будем исходить из определения общего решения и просто проверим, что семейство функций у(ж), определяемое формулой (4), удовлетворяет условиям 1) и 2), содержащимся в этом определении. В самом деле, функция у(х), определяемая формулой (4), является решением уравнения (2) при любых значениях постоянных, поскольку сумма какого-либо решения неоднородного уравнения и любого решения соответствующего однородного уравнения есть решение неоднородного уравнения. Так как для уравнения (2) при х 6 [а, Ь] выполнены условия теоремы 1 существования и единственности решения задачи Коши, то остается показать, что подбором постоянных С, в (4) можно удовлетворить произвольно заданным начальным условиям где хо € (а,6), т.е. можно решить любую задачу Коши. Ограничимся случаем, когда п = 3. Потребовав, чтобы решение (4) удовлетворяло начальным условиям (5), приходим к системе уравнений для отыскания Эта линейная по отношению к система трех уравнений с тремя неизвестными допускает единственное решение относительно з при произвольных правых частях, так как определитель этой системы есть определитель Вронского W(x$) для линейно независимой системы решений соответствующего однородного уравнения и, следовательно, отличен от нуля в любой точке ж € (а, Ь), в частности в точке ж = жо.
уо, Уо> Уо» найдется решение С?, С?, Cj системы (6) такое, что функция будет решением дифференциального уравнения (2), удовлетворяющим начальным условиям Линейные однородные дифференциальные уравнения с постоянными коэффициентами Общий случай: уравнение произвольного порядка Физические приложения: уравнение колебаний. Уравнения, приводящие к уравнениям с постоянными коэффициентами Линейные неоднородные дифференциальные уравнения Из этой теоремы следует, что задача нахождения общего решения линейного неоднородного уравнения сводится к отысканию какого-либо частного решения этого неоднородного уравнения и общего решения соответствующего однородного уравнения. Интегрирование линейного неоднородного дифференциального уравнения методом вариации постоянных 155 Пример 1. Найти общее решение уравнения М Нетрудно заметить, что функция является частным решением данного неоднородного уравнения. Чтобы найти общее решение этого уравнения, остается отыскать общее решение соответствующего однородного уравнения Это уравнение есть линейное однородное уравнение с постоянными коэффициентами. Характеристическое уравнение, соответствующее уравнению , есть корни его Поэтому общее решение уравнения (*) имеет вид . Общее решение исходного неоднородного уравнения: Присылайте задания в любое время дня и ночи в ➔ Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института. Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды. Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги. Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать  Линейные дифференциальные уравнения с постоянными коэффициентамиЛинейное дифференциальное уравнение (*) назовём уравнением с постоянными коэффициентами, если в этом уравнении коэффициенты постоянны, то есть ai(x)=const. Тогда соответствующее однородное уравнение L(y)=0 будет иметь вид Пример №1 . Для уравнения y»-3y’ + 2y=0 корни характеристического уравнения r 2 — 3r + 2 = 0 равны r1 = 1, r2 = 2 (корни были найдены через сервис нахождения дискриминанта). Следовательно, фундаментальную систему решений составляют функции y1 = e x , y2 = e 2 x , а общее решение записывается в виде y = C1e x + C2e 2 x . Пример №2 . Для уравнения y»’-4y»+4y’ = 0 характеристическое уравнение r 3 -4r 2 + 4r = 0 имеет корни r=0 кратности 1 и r=2 кратности 2, так как r 3 -4r 2 + 4r = r(r-2) 2 , поэтому фундаментальной системой решений исходного уравнения является система функций y1 = 1, y2 = e 2 x , y3 = xe 2 x , а общее решение имеет вид y = C1 + C2e 2 x + C3xe 2 x . 📽️ ВидеоЛинейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать  Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать  Дифференциальные уравнения, 1 урок, Дифференциальные уравнения. Основные понятияСкачать  Частное решение дифференциального уравнения. 11 класс.Скачать  Дифференциальные уравнения. 11 класс.Скачать  Определяем тип ДУ 1Скачать  Откуда появляются дифференциальные уравнения и как их решатьСкачать  Математика без Ху!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.Скачать  Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать  Определение типов дифференциальных уравнений первого порядка...Скачать  Линейное дифференциальное уравнение первого порядка (1-x^2)*y'-xy=1Скачать  Решение дифференциальных уравнений. Практическая часть. 11 класс.Скачать  Основные понятия дифференциальных уравнений от bezbotvyСкачать  2. Дифференциальные уравнения с разделяющимися переменными. Часть 1.Скачать  9. Метод вариации произвольной постоянной ( метод Лагранжа ). Линейные дифференциальные уравнения.Скачать  Линейное неоднородное дифференциальное уравнение 2 способаСкачать  |
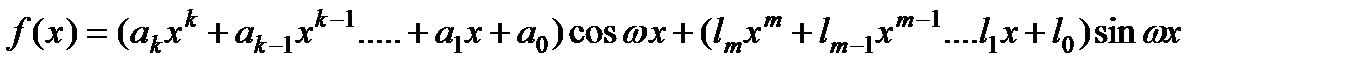
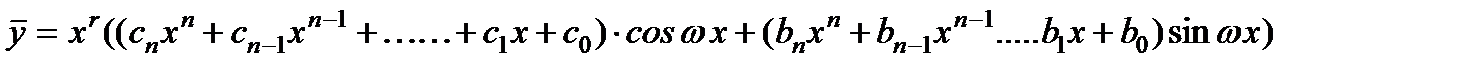



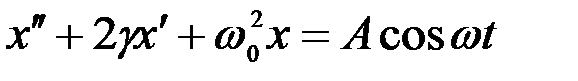
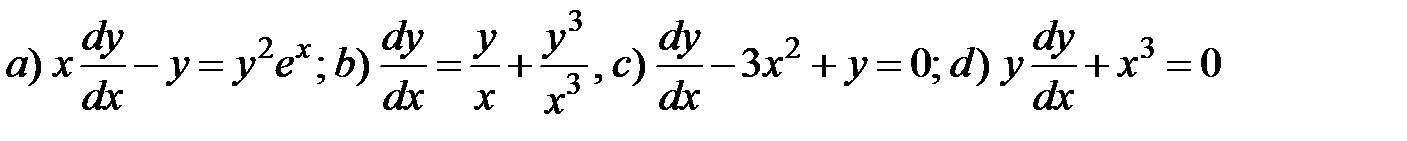
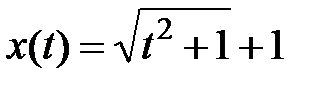
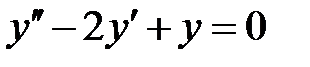
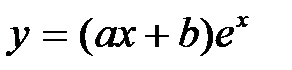


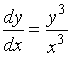
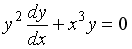
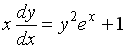
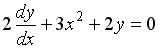
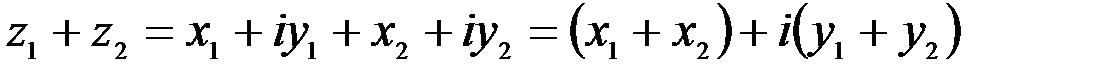 .
.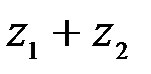 изображается вектором – суммой векторов
изображается вектором – суммой векторов 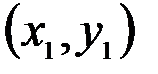 и
и  .
.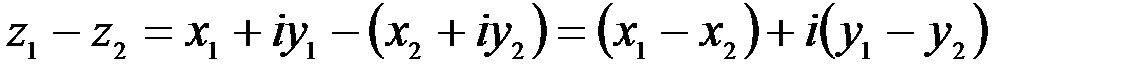 .
.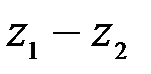 изображается вектором – разностью векторов
изображается вектором – разностью векторов 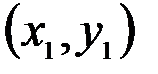 и
и 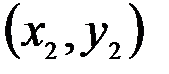 .
.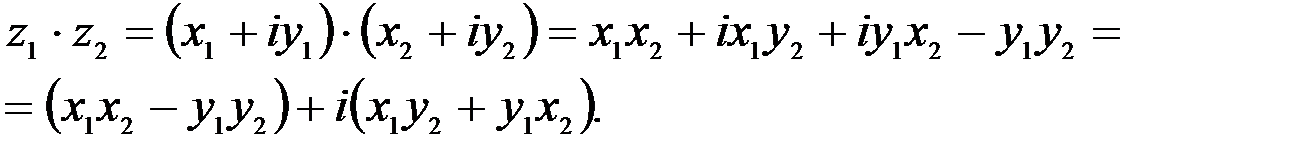
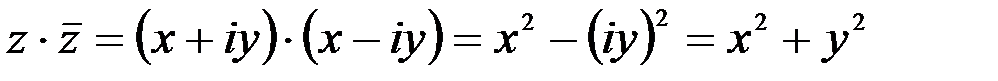 .
.
 при
при 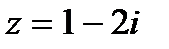 .
.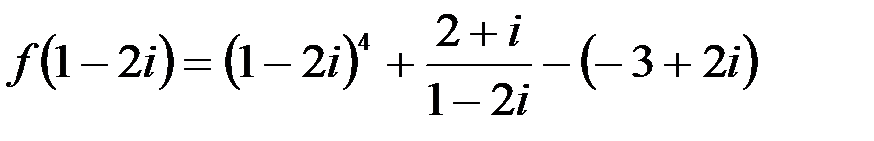 . Для вычисления первого слагаемого воспользуемся формулой бинома Ньютона:
. Для вычисления первого слагаемого воспользуемся формулой бинома Ньютона:
 .
.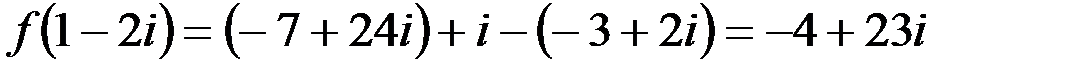 .
.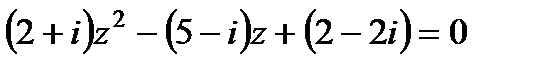 .
. .
. , получим:
, получим: 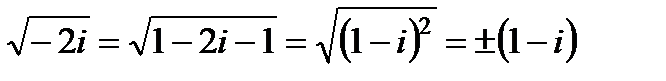 .
. . Отсюда
. Отсюда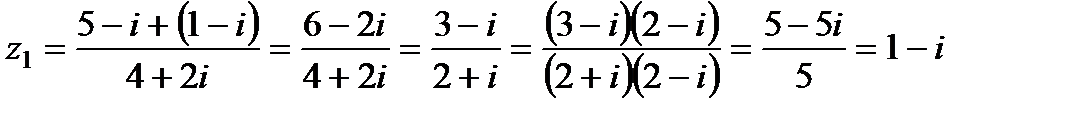
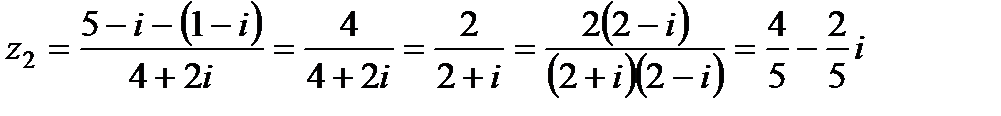 .
.














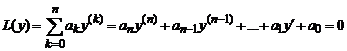 . (6)
. (6) 