Как определить когда прямые пересекаются уравнения

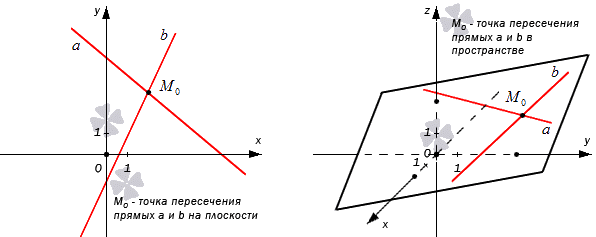
Если точка M, является точкой пересечения двух прямых, то она должна принадлежать этим прямым, а ее координаты удовлетворять уравнения этих прямых.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Точка пересечения двух прямых на плоскости

Если система уравнений:

• имеет единственное решение, то прямые пересекаются;
• имеет бесконечное множество решений, то прямые совпадают;
• не имеет решений, то прямые не пересекаются (прямые параллельны между собой)

Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:

y = 2 x — 1 y = -3 x + 1

Вычтем из первого уравнения второе

y — y = 2 x — 1 — (-3 x + 1) y = -3 x + 1 => 0 = 5 x — 2 y = -3 x + 1

Из первого уравнения найдем значение x

5 x = 2 y = -3 x + 1 => x = 2 5 = 0.4 y = -3 x + 1

Подставим значение x во второе уравнение и найдем значение y

x = 0.4 y = -3·(0.4) + 1 = -1.2 + 1 = -0.2

Ответ. Точка пересечения двух прямых имеет координаты (0.4, -0.2)

Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:

y = 2 x — 1 x = 2 t + 1 y = t

В первое уравнение подставим значения x и y из второго и третьего уравнений.

t = 2·(2 t + 1) — 1 x = 2 t + 1 y = t => t = 4 t + 1 x = 2 t + 1 y = t =>

-3 t = 1 x = 2 t + 1 y = t => t = — 1 3 x = 2 t + 1 y = t

Подставим значение t во второе и третье уравнение

t = — 1 3 x = 2·(- 1 3 ) + 1 = — 2 3 + 1 = 1 3 y = — 1 3

Ответ. Точка пересечения двух прямых имеет координаты ( 1 3 , — 1 3 )

Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:

2 x + 3 y = 0 x — 2 3 = y 4

Из второго уравнения выразим y через x

2 x + 3 y = 0 y = 4· x — 2 3

Подставим y в первое уравнение

2 x + 3·4· x — 2 3 = 0 y = 4· x — 2 3 => 2 x + 4·( x — 2) = 0 y = 4· x — 2 3 =>

2 x + 4 x — 8 = 0 y = 4· x — 2 3 => 6 x = 8 y = 4· x — 2 3 =>

x = 8 6 = 4 3 y = 4· x — 2 3 => x = 8 6 = 4 3 y = 4· 4/3 — 2 3 = 4· -2/3 3 = — 8 9

Ответ. Точка пересечения двух прямых имеет координаты ( 4 3 , — 8 9 )

Решение: Обе прямые заданы уравнениями с угловым коэффициентом. Так как k ₁ = k ₂ = 2, то прямые параллельны. Так как эти прямые не совпадают то точек пересечения нет.

Решим также эту задачу используя систему уравнений:

y = 2 x — 1 y = 2 x + 1

Вычтем из первого уравнения второе

y — y = 2 x — 1 — (2 x + 1) y = -3 x + 1 => 0 = -2 y = -3 x + 1

В первом уравнении получили противоречие (0 ≠ -2), значит система не имеет решений — отсутствуют точки пересечения прямых (прямые параллельны).

Ответ. Прямые не пересекаются (прямые параллельны).

Решение: Подставим координаты точки N в уравнения прямых.

Ответ. Так как оба уравнения превратились в тождества, то точка N — точка пересечения этих прямых.

Видео:16. Показать что прямые пересекаются и найти точку их пересечения в пространствеСкачать

Точка пересечения двух прямых в пространстве

Если система уравнений:

• имеет единственное решение, то прямые пересекаются;
• имеет бесконечное множество решений, то прямые совпадают;
• не имеет решений, то прямые не пересекаются (прямые параллельны или скрещиваются между собой)

Решение: Составим систему уравнений

x — 1 = a y — 1 = a z — 1 = a x — 3 -2 = b 2 — y = b z = b => x = a + 1 y = a + 1 z = a + 1 x — 3 -2 = b 2 — y = b z = b =>

Подставим значения x , y , z из 1, 2, 3 уравнений в 4, 5, 6 уравнения

x = a + 1 y = a + 1 z = a + 1 a + 1 — 3 -2 = b 2 — ( a + 1) = b a + 1 = b => x = a + 1 y = a + 1 z = a + 1 a — 2 -2 = b 1 — a = b a + 1 = b

К шестому уравнению добавим пятое уравнение

x = a + 1 y = a + 1 z = a + 1 a — 2 -2 = b 1 — a = b a + 1 + (1 — a ) = b + b => x = a + 1 y = a + 1 z = a + 1 a — 2 -2 = b 1 — a = b b = 1

Подставим значение b в четвертое и пятое уравнения

x = a + 1 y = a + 1 z = a + 1 a — 2 -2 = 1 1 — a = 1 b = 1 => x = a + 1 y = a + 1 z = a + 1 a — 2 = -2 a = 0 b = 1 =>

x = a + 1 y = a + 1 z = a + 1 a = 0 a = 0 b = 1 => x = 0 + 1 = 1 y = 0 + 1 = 1 z = 0 + 1 = 1 a = 0 a = 0 b = 1

Ответ. Прямые пересекаются в точке с координатами (1, 1, 1).

Решение: Составим систему уравнений заменив во втором уравнении параметр t на a

x = 2 t — 3 y = t z = — t + 2 x = a + 1 y = 3 a — 2 z = 3

Подставим значения x , y , z из 1, 2, 3 уравнений в 4, 5, 6 уравнения

x = 2 t — 3 y = t z = — t + 2 2 t — 3 = a + 1 t = 3 a — 2 — t + 2 = 3 => x = 2 t — 3 y = t z = — t + 2 2 t = a + 4 t = 3 a — 2 t = -1 =>

Подставим значение t из шестого уравнения в остальные уравнения

x = 2·(-1) — 3 y = (-1) z = -(-1) + 2 2·(-1) = a + 4 -1 = 3 a — 2 t = -1 => x = -5 y = -1 z = 3 a = -6 a = 1 3 t = -1

Ответ. Так как -6 ≠ 1 3 , то прямые не пересекаются.

Видео:17. Показать что прямые пересекаются и составить уравнение плоскости в которой они расположеныСкачать

Координаты точки пересечения двух прямых — примеры нахождения

Для того, чтобы решить геометрическую задачу методом координат, необходима точка пересечения, координаты которой используются при решении. Возникает ситуация, когда требуется искать координаты пересечения двух прямых на плоскости или определить координаты тех же прямых в пространстве. Данная статья рассматривает случаи нахождения координат точек, где пересекаются заданные прямые.

Видео:№976. Найдите координаты точки пересечения прямых 4x + 3y-6 = 0 и 2х+у-4 = 0.Скачать

Точка пересечения двух прямых – определение

Необходимо дать определение точкам пересечения двух прямых.

Раздел взаимного расположения прямых на плоскости показывает, что они могут совпадать , быть параллельными, пересекаться в одной общей точке или скрещивающимися. Две прямые, находящиеся в пространстве, называют пересекающимися, если они имеют одну общую точку.

Определение точки пересечения прямых звучит так:

Точка, в которой пересекаются две прямые, называют их точкой пересечения. Иначе говоря, что точка пересекающихся прямых и есть точка пересечения.

Рассмотрим на рисунке, приведенном ниже.

Видео:Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Нахождение координат точки пересечения двух прямых на плоскости

Перед нахождением координат точки пересечения двух прямых, необходимо рассмотреть предлагаемый ниже пример.

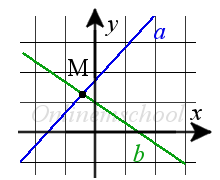
Если на плоскости имеется система координат О х у , то задаются две прямые a и b . Прямой a соответствует общее уравнение вида A 1 x + B 1 y + C 1 = 0 , для прямой b — A 2 x + B 2 y + C 2 = 0 . Тогда M 0 ( x 0 , y 0 ) является некоторой точкой плоскости необходимо выявить , будет ли точка М 0 являться точкой пересечения этих прямых.

Чтобы решить поставленную задачу, необходимо придерживаться определения. Тогда прямые должны пересекаться в точке, координаты которой являются решением заданных уравнений A 1 x + B 1 y + C 1 = 0 и A 2 x + B 2 y + C 2 = 0 . Значит, координаты точки пересечения подставляются во все заданные уравнения. Если они при подстановке дают верное тождество, тогда M 0 ( x 0 , y 0 ) считается их точкой пересечения.

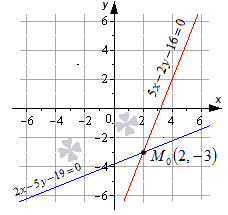
Даны две пересекающиеся прямые 5 x — 2 y — 16 = 0 и 2 x — 5 y — 19 = 0 . Будет ли точка М 0 с координатами ( 2 , — 3 ) являться точкой пересечения.

Чтобы пересечение прямых было действительным, необходимо, чтобы координаты точки М 0 удовлетворяли уравнениям прямых. Это проверяется при помощи их подстановки. Получаем, что

5 · 2 — 2 · ( — 3 ) — 16 = 0 ⇔ 0 = 0 2 · 2 — 5 · ( — 3 ) — 19 = 0 ⇔ 0 = 0

Оба равенства верные, значит М 0 ( 2 , — 3 ) является точкой пересечения заданных прямых.

Изобразим данное решение на координатной прямой рисунка, приведенного ниже.

Ответ: заданная точка с координатами ( 2 , — 3 ) будет являться точкой пересечения заданных прямых.

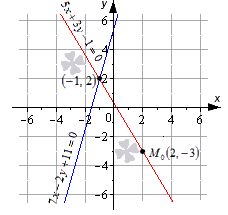
Пересекутся ли прямые 5 x + 3 y — 1 = 0 и 7 x — 2 y + 11 = 0 в точке M 0 ( 2 , — 3 ) ?

Для решения задачи необходимо подставить координаты точки во все уравнения. Получим, что

5 · 2 + 3 · ( — 3 ) — 1 = 0 ⇔ 0 = 0 7 · 2 — 2 · ( — 3 ) + 11 = 0 ⇔ 31 = 0

Второе равенство не является верным, значит, что заданная точка не принадлежит прямой 7 x — 2 y + 11 = 0 . Отсюда имеем, что точка М 0 не точка пересечения прямых.

Чертеж наглядно показывает, что М 0 — это не точка пересечения прямых. Они имеют общую точку с координатами ( — 1 , 2 ) .

Ответ: точка с координатами ( 2 , — 3 ) не является точкой пересечения заданных прямых.

Переходим к нахождению координат точек пересечения двух прямых при помощи заданных уравнений на плоскости.

Задаются две пересекающиеся прямые a и b уравнениями вида A 1 x + B 1 y + C 1 = 0 и A 2 x + B 2 y + C 2 = 0 , расположенных в О х у . При обозначении точки пересечения М 0 получим, что следует продолжить поиск координат по уравнениям A 1 x + B 1 y + C 1 = 0 и A 2 x + B 2 y + C 2 = 0 .

Из определения очевидно, что М 0 является общей точкой пересечения прямых. В этом случае ее координаты должны удовлетворять уравнениям A 1 x + B 1 y + C 1 = 0 и A 2 x + B 2 y + C 2 = 0 . Иными словами это и есть решение полученной системы A 1 x + B 1 y + C 1 = 0 A 2 x + B 2 y + C 2 = 0 .

Значит, для нахождения координат точки пересечения , необходимо все уравнения добавить в систему и решить ее.

Заданы две прямые x — 9 y + 14 = 0 и 5 x — 2 y — 16 = 0 на плоскости. необходимо найти их пересечение.

Данные по условию уравнения необходимо собрать в систему, после чего получим x — 9 y + 14 = 0 5 x — 2 y — 16 = 0 . Чтобы решить его, разрешается первое уравнение относительно x , подставляется выражение во второе:

x — 9 y + 14 = 0 5 x — 2 y — 16 = 0 ⇔ x = 9 y — 14 5 x — 2 y — 16 = 0 ⇔ ⇔ x = 9 y — 14 5 · 9 y — 14 — 2 y — 16 = 0 ⇔ x = 9 y — 14 43 y — 86 = 0 ⇔ ⇔ x = 9 y — 14 y = 2 ⇔ x = 9 · 2 — 14 y = 2 ⇔ x = 4 y = 2

Получившиеся числа являются координатами, которые необходимо было найти.

Ответ: M 0 ( 4 , 2 ) является точкой пересечения прямых x — 9 y + 14 = 0 и 5 x — 2 y — 16 = 0 .

Поиск координат сводится к решению системы линейных уравнений. Если по условию дан другой вид уравнения, тогда следует привести его к нормальному виду.

Определить координаты точек пересечения прямых x — 5 = y — 4 — 3 и x = 4 + 9 · λ y = 2 + λ , λ ∈ R .

Для начала необходимо привести уравнения к общему виду. Тогда получаем, что x = 4 + 9 · λ y = 2 + λ , λ ∈ R преобразуется таким образом:

x = 4 + 9 · λ y = 2 + λ ⇔ λ = x — 4 9 λ = y — 2 1 ⇔ x — 4 9 = y — 2 1 ⇔ ⇔ 1 · ( x — 4 ) = 9 · ( y — 2 ) ⇔ x — 9 y + 14 = 0

После чего беремся за уравнение канонического вида x — 5 = y — 4 — 3 и преобразуем. Получаем, что

x — 5 = y — 4 — 3 ⇔ — 3 · x = — 5 · y — 4 ⇔ 3 x — 5 y + 20 = 0

Отсюда имеем, что координаты – это точка пересечения

x — 9 y + 14 = 0 3 x — 5 y + 20 = 0 ⇔ x — 9 y = — 14 3 x — 5 y = — 20

Применим метод Крамера для нахождения координат:

∆ = 1 — 9 3 — 5 = 1 · ( — 5 ) — ( — 9 ) · 3 = 22 ∆ x = — 14 — 9 — 20 — 5 = — 14 · ( — 5 ) — ( — 9 ) · ( — 20 ) = — 110 ⇒ x = ∆ x ∆ = — 110 22 = — 5 ∆ y = 1 — 14 3 — 20 = 1 · ( — 20 ) — ( — 14 ) · 3 = 22 ⇒ y = ∆ y ∆ = 22 22 = 1

Ответ: M 0 ( — 5 , 1 ) .

Имеется еще способ для нахождения координат точки пересечения прямых, находящихся на плоскости. Он применим, когда одна из прямых задается параметрическими уравнениями, имеющими вид x = x 1 + a x · λ y = y 1 + a y · λ , λ ∈ R . Тогда вместо значения x подставляется x = x 1 + a x · λ и y = y 1 + a y · λ , где получим λ = λ 0 , соответствующее точке пересечения, имеющей координаты x 1 + a x · λ 0 , y 1 + a y · λ 0 .

Определить координаты точки пересечения прямой x = 4 + 9 · λ y = 2 + λ , λ ∈ R и x — 5 = y — 4 — 3 .

Необходимо выполнить подстановку в x — 5 = y — 4 — 3 выражением x = 4 + 9 · λ , y = 2 + λ , тогда получим:

4 + 9 · λ — 5 = 2 + λ — 4 — 3

При решении получаем, что λ = — 1 . Отсюда следует, что имеется точка пересечения между прямыми x = 4 + 9 · λ y = 2 + λ , λ ∈ R и x — 5 = y — 4 — 3 . Для вычисления координат необходимо подставить выражение λ = — 1 в параметрическое уравнение. Тогда получаем, что x = 4 + 9 · ( — 1 ) y = 2 + ( — 1 ) ⇔ x = — 5 y = 1 .

Ответ: M 0 ( — 5 , 1 ) .

Для полного понимания темы, необходимо знать некоторые нюансы.

Предварительно необходимо понять расположение прямых. При их пересечении мы найдем координаты, в других случаях решения существовать не будет. Чтобы не делать эту проверку, можно составлять систему вида A 1 x + B 1 y + C 1 = 0 A 2 x + B 2 + C 2 = 0 При наличии решения делаем вывод о том, что прямые пересекаются. Если решение отсутствует, то они параллельны. Когда система имеет бесконечное множество решений, тогда говорят, что они совпадают.

Даны прямые x 3 + y — 4 = 1 и y = 4 3 x — 4 . Определить, имеют ли они общую точку.

Упрощая заданные уравнения, получаем 1 3 x — 1 4 y — 1 = 0 и 4 3 x — y — 4 = 0 .

Следует собрать уравнения в систему для последующего решения:

1 3 x — 1 4 y — 1 = 0 1 3 x — y — 4 = 0 ⇔ 1 3 x — 1 4 y = 1 4 3 x — y = 4

Отсюда видно, что уравнения выражаются друг через друга, тогда получим бесконечное множество решений. Тогда уравнения x 3 + y — 4 = 1 и y = 4 3 x — 4 определяют одну и ту же прямую. Поэтому нет точек пересечения.

Ответ: заданные уравнения определяют одну и ту же прямую.

Найти координаты точки пересекающихся прямых 2 x + ( 2 — 3 ) y + 7 = 0 и 2 3 + 2 x — 7 y — 1 = 0 .

По условию возможно такое, прямые не будут пересекаться. Необходимо составить систему уравнений и решать. Для решения необходимо использовать метод Гаусса, так как с его помощью есть возможность проверить уравнение на совместимость. Получаем систему вида:

2 x + ( 2 — 3 ) y + 7 = 0 2 ( 3 + 2 ) x — 7 y — 1 = 0 ⇔ 2 x + ( 2 — 3 ) y = — 7 2 ( 3 + 2 ) x — 7 y = 1 ⇔ ⇔ 2 x + 2 — 3 y = — 7 2 ( 3 + 2 ) x — 7 y + ( 2 x + ( 2 — 3 ) y ) · ( — ( 3 + 2 ) ) = 1 + — 7 · ( — ( 3 + 2 ) ) ⇔ ⇔ 2 x + ( 2 — 3 ) y = — 7 0 = 22 — 7 2

Получили неверное равенство, значит система не имеет решений. Делаем вывод, что прямые являются параллельными. Точек пересечения нет.

Второй способ решения.

Для начала нужно определить наличие пересечения прямых.

n 1 → = ( 2 , 2 — 3 ) является нормальным вектором прямой 2 x + ( 2 — 3 ) y + 7 = 0 , тогда вектор n 2 → = ( 2 ( 3 + 2 ) , — 7 — нормальный вектор для прямой 2 3 + 2 x — 7 y — 1 = 0 .

Необходимо выполнить проверку коллинеарности векторов n 1 → = ( 2 , 2 — 3 ) и n 2 → = ( 2 ( 3 + 2 ) , — 7 ) . Получим равенство вида 2 2 ( 3 + 2 ) = 2 — 3 — 7 . Оно верное, потому как 2 2 3 + 2 — 2 — 3 — 7 = 7 + 2 — 3 ( 3 + 2 ) 7 ( 3 + 2 ) = 7 — 7 7 ( 3 + 2 ) = 0 . Отсюда следует, что векторы коллинеарны. Значит, прямые являются параллельными и не имеют точек пересечения.

Ответ: точек пересечения нет, прямые параллельны.

Найти координаты пересечения заданных прямых 2 x — 1 = 0 и y = 5 4 x — 2 .

Для решения составляем систему уравнений. Получаем

2 x — 1 = 0 5 4 x — y — 2 = 0 ⇔ 2 x = 1 5 4 x — y = 2

Найдем определитель основной матрицы. Для этого 2 0 5 4 — 1 = 2 · ( — 1 ) — 0 · 5 4 = — 2 . Так как он не равен нулю, система имеет 1 решение. Отсюда следует, что прямые пересекаются. Решим систему для нахождения координат точек пересечения:

2 x = 1 5 4 x — y = 2 ⇔ x = 1 2 4 5 x — y = 2 ⇔ x = 1 2 5 4 · 1 2 — y = 2 ⇔ x = 1 2 y = — 11 8

Получили, что точка пересечения заданных прямых имеет координаты M 0 ( 1 2 , — 11 8 ) .

Ответ: M 0 ( 1 2 , — 11 8 ) .

Видео:Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

Нахождения координат точки пересечения двух прямых в пространстве

Таким же образом находятся точки пересечения прямых пространства.

Когда заданы прямые a и b в координатной плоскости О х у z уравнениями пересекающихся плоскостей, то имеется прямая a , которая может быть определена при помощи заданной системы A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 1 = 0 а прямая b — A 3 x + B 3 y + C 3 z + D 3 = 0 A 4 x + B 4 y + C 4 z + D 4 = 0 .

Когда точка М 0 является точкой пересечения прямых, тогда ее координаты должны быть решениями обоих уравнений. Получим линейные уравнения в системе:

A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A 3 x + B 3 y + C 3 z + D 3 = 0 A 4 x + B 4 y + C 4 z + D 4 = 0

Рассмотрим подобные задания на примерах.

Найти координаты точки пересечения заданных прямых x — 1 = 0 y + 2 z + 3 = 0 и 3 x + 2 y + 3 = 0 4 x — 2 z — 4 = 0

Составляем систему x — 1 = 0 y + 2 z + 3 = 0 3 x + 2 y + 3 = 0 4 x — 2 z — 4 = 0 и решим ее. Чтобы найти координаты, необходимо решать через матрицу. Тогда получим основную матрицу вида A = 1 0 0 0 1 2 3 2 0 4 0 — 2 и расширенную T = 1 0 0 1 0 1 2 — 3 4 0 — 2 4 . Определяем ранг матрицы по Гауссу.

1 = 1 ≠ 0 , 1 0 0 1 = 1 ≠ 0 , 1 0 0 0 1 2 3 2 0 = — 4 ≠ 0 , 1 0 0 1 0 1 2 — 3 3 2 0 — 3 4 0 — 2 4 = 0

Отсюда следует, что ранг расширенной матрицы имеет значение 3 . Тогда система уравнений x — 1 = 0 y + 2 z + 3 = 0 3 x + 2 y + 3 = 0 4 x — 27 — 4 = 0 в результате дает только одно решение.

Базисный минор имеет определитель 1 0 0 0 1 2 3 2 0 = — 4 ≠ 0 , тогда последнее уравнение не подходит. Получим, что x — 1 = 0 y + 2 z + 3 = 0 3 x + 2 y + 3 = 0 4 x — 2 z — 4 = 0 ⇔ x = 1 y + 2 z = — 3 3 x + 2 y — 3 . Решение системы x = 1 y + 2 z = — 3 3 x + 2 y = — 3 ⇔ x = 1 y + 2 z = — 3 3 · 1 + 2 y = — 3 ⇔ x = 1 y + 2 z = — 3 y = — 3 ⇔ ⇔ x = 1 — 3 + 2 z = — 3 y = — 3 ⇔ x = 1 z = 0 y = — 3 .

Значит, имеем, что точка пересечения x — 1 = 0 y + 2 z + 3 = 0 и 3 x + 2 y + 3 = 0 4 x — 2 z — 4 = 0 имеет координаты ( 1 , — 3 , 0 ) .

Ответ: ( 1 , — 3 , 0 ) .

Система вида A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A 3 x + B 3 y + C 3 z + D 3 = 0 A 4 x + B 4 y + C 4 z + D 4 = 0 имеет только одно решение. Значит, прямые a и b пересекаются.

В остальных случаях уравнение не имеет решения, то есть и общих точек тоже. То есть невозможно найти точку с координатами, так как ее нет.

Поэтому система вида A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A 3 x + B 3 y + C 3 z + D 3 = 0 A 4 x + B 4 y + C 4 z + D 4 = 0 решается методом Гаусса. При ее несовместимости прямые не являются пересекающимися. Если решений бесконечное множество, то они совпадают.

Можно произвести решение при помощи вычисления основного и расширенного ранга матрицы, после чего применить теорему Кронекера-Капелли. Получим одно, множество или полное отсутствие решений.

Заданы уравнения прямых x + 2 y — 3 z — 4 = 0 2 x — y + 5 = 0 и x — 3 z = 0 3 x — 2 y + 2 z — 1 = 0 . Найти точку пересечения.

Для начала составим систему уравнений. Получим, что x + 2 y — 3 z — 4 = 0 2 x — y + 5 = 0 x — 3 z = 0 3 x — 2 y + 2 z — 1 = 0 . решаем ее методом Гаусса:

1 2 — 3 4 2 — 1 0 — 5 1 0 — 3 0 3 — 2 2 1

1 2 — 3 4 0 — 5 6 — 13 0 — 2 0 — 4 0 — 8 11 — 11

1 2 — 3 4 0 — 5 6 — 13 0 0 — 12 5 6 5 0 0 7 5 — 159 5

1 2 — 3 4 0 — 5 6 — 13 0 0 — 12 5 6 5 0 0 0 311 10

Очевидно, что система не имеет решений, значит прямые не пересекаются. Точки пересечения нет.

Ответ: нет точки пересечения.

Если прямые заданы при помощи кононических или параметрических уравнений, нужно привести к виду уравнений пересекающихся плоскостей, после чего найти координаты.

Заданы две прямые x = — 3 — λ y = — 3 · λ z = — 2 + 3 · λ , λ ∈ R и x 2 = y — 3 0 = z 5 в О х у z . Найти точку пересечения.

Задаем прямые уравнениями двух пересекающихся плоскостей. Получаем, что

x = — 3 — λ y = — 3 · λ z = — 2 + 3 · λ ⇔ λ = x + 3 — 1 λ = y — 3 λ = z + 2 3 ⇔ x + 3 — 1 = y — 3 = z + 2 3 ⇔ ⇔ x + 3 — 1 = y — 3 x + 3 — 1 = z + 2 3 ⇔ 3 x — y + 9 = 0 3 x + z + 11 = 0 x 2 = y — 3 0 = z 5 ⇔ y — 3 = 0 x 2 = z 5 ⇔ y — 3 = 0 5 x — 2 z = 0

Находим координаты 3 x — y + 9 = 0 3 x + z + 11 = 0 y — 3 = 0 5 x — 2 z = 0 , для этого посчитаем ранги матрицы. Ранг матрицы равен 3 , а базисный минор 3 — 1 0 3 0 1 0 1 0 = — 3 ≠ 0 , значит, что из системы необходимо исключить последнее уравнение. Получаем, что

3 x — y + 9 = 0 3 x + z + 11 = 0 y — 3 = 0 5 x — 2 z = 0 ⇔ 3 x — y + 9 = 0 3 x + z + 11 = 0 y — 3 = 0

Решим систему методом Крамер. Получаем, что x = — 2 y = 3 z = — 5 . Отсюда получаем, что пересечение заданных прямых дает точку с координатами ( — 2 , 3 , — 5 ) .

Видео:Составляем уравнение прямой по точкамСкачать

Точка пересечения двух прямых на плоскости

Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Пересечение прямых

Для создания компьютерных игр, программ математических графиков, расчетов движения объектов и т.п. очень часто требуется найти точку пресечения прямых. Сначала необходимо на бумаге вывести и упростить формулы вычисления и далее эти формулы перевести в программный код.

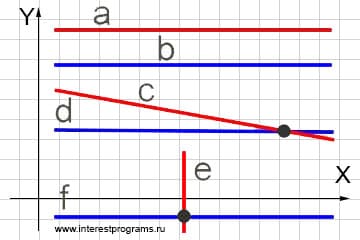
Прямые это бесконечные линии, поэтому на плоскости они всегда пересекаются. Если прямые не пересекаются значит они параллельны. Частные случаи поведения прямых на плоскости: прямые неопределенны, прямые параллельны, прямые совпадают, одна из прямых параллельна оси X или Y. Общие случаи «нормального» пересечения прямых и частные случаи учитываются в программном коде класса Intersections прикрепленного исходника.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Прямые пересекаются

Даны две прямые AB и CD расположенные на одной плоскости. Они пересекаются и необходимо найти точку пересечения. За основу берем классическое уравнение прямой и подставляя данные получаем систему уравнений для двух прямых.

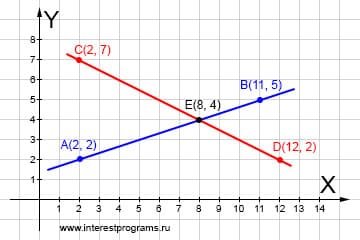
Точку пересечения можно найти, решая совместно уравнения прямых. Два уравнения — две неизвестных величины. Если количество уравнений больше или равно количеству неизвестных, то система решаема. Точка пересечения двух прямых это такая точка, которая принадлежит обеим прямым.

Классическое уравнение прямой: Запишем уравнение в одну строчку: Вычислим коэффициенты и свободные члены: В итоге получаем уравнение прямой с коэффициентами:

Уравнение с линейными коэффициентами отличается от уравнения с угловым коэффициентом отсутствием операции деления. Минимум операций деления упрощает создание устойчивого программного кода.

Видео:15. Взаимное расположение прямых в пространствеСкачать

Точка пересечения прямых

Координаты точки пересечения это числа которые являются решением для каждого из уравнений прямых. Решая систему из двух уравнений находим в какой точке пересекаются прямые AB и CD.

Подставляем известные данные: Получаем два уравнения: Решаем систему уравнений: Найдено, прямые пересекаются в точке с координатами:

Видео:Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

Прямые параллельны

Если прямые параллельны и лежат друг от друга на расстоянии, то у них нет общих точек. Совместная система уравнений не имеет решений. Эти уравнения существуют как бы сами по себе. В точности как их параллельные прямые.

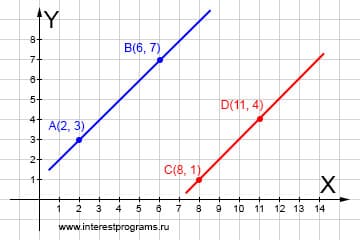
Две прямые могут полностью совпадать, в таком случае у них бесконечное количество общих точек. Совпадение прямых означает равность коэффициентов и свободных членов уравнений. Совпадающие прямые имеют идентичные уравнения.

Применяя формулу у.2 выведем уравнения прямых: Получаем систему уравнений:

Итог: система уравнений параллельных прямых не имеет решений.

Видео:найти уравнения биссектрис углов между прямымиСкачать

Уравнение в программный код

На бумаге всё славненько, надо также сделать и в программном коде. Но программы не разбираются в уравнениях, им подавай переменные, постоянные и функции. Программный код не терпит неопределенности, он требует точные данные. Очень желательно строить выражения без операций деления. Преобразуем в программный код уравнение с коэффициентами (у.3) описанное выше. Для каждой прямой своё уравнение и переменные.

Точки определяющие прямые запишем в структуры Point. У каждой прямой две точки и они являются входными данными:
Определяем коэффициенты и свободные члены уравнений. Записываем их в соответствующие переменные:
Точка пересечения также будет храниться в структуре Point:

Видео:Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Вывод результата

В выражениях присутствует деление. Но знаменатель только тогда и только тогда будет равен нулю, когда обе прямые будут параллельны или оси X или оси Y. В этом случае они не пересекаются или совпадают. Это отслеживаемые состояния в классе Intersections , и вывод информации заканчивается до выбрасывания исключения при делении на ноль.

Видео:23. Точка пересечения прямой и плоскости / Проекция точки на плоскость / Проекция точки на прямуюСкачать

Проверка параллельности и совпадения

Видео:Найти точку пересечения прямой и плоскостиСкачать

Проверка на перпендикулярность

Видео:Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Класс Intersections

Исходник представляет собой два класса: класс вычисления точки пересечения прямых и информационный класс выдающий множество дополнительных сведений о свойствах исследуемых прямых.

Краткий листинг исходника дающий представление о структуре классов:

Видео:ПЕРЕСЕЧЕНИЕ прямых | ТОЧКА пересечения | Линейные функцииСкачать

Применение класса Intersections

Класс class Intersections легко встраивается в любой исходный код. Точки определяющие прямые являются входными данными. На выходе получаем результат пересечения, координаты точки пересечения. Для дальнейшей обработки результатов можно использовать идентификатор свойства пересечения и дополнительную текстовую информацию.

Видео:Взаимное расположение прямых на плоскости. 7 класс.Скачать

Прикрепленный файл

Прикрепленный файл архива содержит исходник классов Intersections, Info и программу демонстрирующую работу класса Intersections в режиме вычисления точки пересечения прямых на плоскости. Исходный код написан на языке C#, но его легко можно преобразовать в код на другом языке программирования. Для работы демонстрационной программы необходима установка платформы. .NET Core 3.1.

Скачать исходник

• Файл: IntersectionsLineLine.zip
• Размер: 84 Кбайт
• Загрузки: 548

Похожая тематика

Пересечение луча и прямой на плоскости »

📽️ Видео

6 класс, 23 урок, Пересечение прямыхСкачать

Точки пересечения графиков линейных функций. 7 класс.ОбразовательныйСкачать