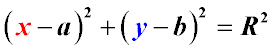Аналитическая геометрия дает единообразные приемы решения геометрических задач. Для этого все заданные и искомые точки и линии относят к одной системе координат.
В системе координат можно каждую точку охарактеризовать ее координатами, а каждую линию – уравнением с двумя неизвестными, графиком которого эта линия является. Таким образом геометрическая задача сводится к алгебраической, где хорошо отработаны все приемы вычислений.
Окружность есть геометрическое место точек с одним определенным свойством (каждая точка окружности равноудалена от одной точки, называется центром). Уравнение окружности должно отражать это свойство, удовлетворять этому условию.
Геометрическая интерпретация уравнения окружности – это линия окружности.
Если поместить окружность в систему координат, то все точки окружности удовлетворяют одному условию – расстояние от них до центра окружности должно быть одинаковым и равным окружности.
Окружность с центром в точке А и радиусом R поместим в координатную плоскость.
Если координаты центра (а;b), а координаты любой точки окружности (х; у), то уравнение окружности имеет вид:
Если квадрат радиуса окружности равен сумме квадратов разностей соответствующих координат любой точки окружности и ее центра, то это уравнение является уравнением окружности в плоской системе координат.
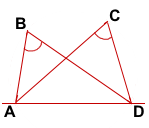
Если центр окружности совпадает с точкой начала координат, то квадрат радиуса окружности равен сумме квадратов координат любой точки окружности. В этом случае уравнение окружности принимает вид:
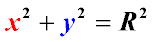
Следовательно, любая геометрическая фигура как геометрическое место точек определяется уравнением, связывающим координаты ее точек. И наоборот, уравнение, связывающее координаты х и у, определяют линию как геометрическое место точек плоскости, координаты которых удовлетворяют данному уравнению.
Видео:Уравнение окружности (1)Скачать

Примеры решения задач про уравнение окружности
Задача. Составить уравнение заданной окружности
Составьте уравнение окружности с центром в точке O (2;-3) и радиусом 4.
Решение.
Обратимся к формуле уравнения окружности:
R 2 = (x- a ) 2 + (y- b ) 2
Подставим значения в формулу.
Радиус окружности R = 4
Координаты центра окружности (в соответствии с условием)
a = 2
b = -3
Получаем:
(x — 2 ) 2 + (y — ( -3 )) 2 = 4 2
или
(x — 2 ) 2 + (y + 3 ) 2 = 16 .
Задача. Принадлежит ли точка уравнению окружности
Проверить, принадлежит ли точка A(2;3) уравнению окружности (x — 2) 2 + (y + 3) 2 = 16.
Решение.
Если точка принадлежит окружности, то ее координаты удовлетворяют уравнению окружности.
Чтобы проверить, принадлежит ли окружности точка с заданными координатами, подставим координаты точки в уравнение заданной окружности.
В уравнение ( x — 2) 2 + ( y + 3) 2 = 16
подставим, согласно условию, координаты точки А(2;3), то есть
x = 2
y = 3
Проверим истинность полученного равенства
( x — 2) 2 + ( y + 3) 2 = 16
( 2 — 2) 2 + ( 3 + 3) 2 = 16
0 + 36 = 16 равенство неверно
Таким образом, заданная точка не принадлежит заданному уравнению окружности.
Видео:9 класс, 6 урок, Уравнение окружностиСкачать

Уравнение окружности.
Окружностью принято обозначать множество всех точек плоскости, равноудаленных от одной точки – от центра.
В формулировке окружности упоминается расстояние между точкой окружности и центром.
Формула расстояния между двумя точками М1(х1; у1) и М2(х2; у2) имеет вид:
,
Применив формулу и формулировку окружности, получаем уравнение окружности с центром в точке С (х0; у0) и радиусом r.
Отметим произвольную точку М(х; у) на этой окружности.
.
Предположим, что М принадлежит окружности с центром С и радиусом r, то МС = r.
Следовательно, МС 2 = r 2 и координаты точки М удовлетворяют уравнению окружности (х – х0 ) 2 +(у – у0 ) 2 = r 2 .
Из выше изложенного делаем вывод, что уравнение окружности с центром в точке С (х0; у0) и радиусом r имеет вид:
В случае когда центр окружности совпадает с началом координат, то получаем частный случай уравнения окружности с центром в точке О (0;0):
Видео:№960. Какие из точек А (3; -4), В(1; 0), С(0; 5),Скачать

Признак принадлежности четырёх точек одной окружности
Признак принадлежности четырёх точек одной окружности
Если точки B и C лежат в одной полуплоскости относительно прямой AD, и точки B и C видны из отрезка AD под одним углом (то есть ∠ABD=∠ACD), то точки A, B, C и D лежат на одной окружности.
Дано: точки B и C лежат в одной полуплоскости относительно прямой AD,
Доказать: точки A, B, C, D лежат на одной окружности
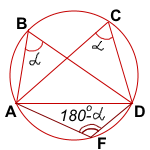
Опишем около треугольника ABD окружность.
Отметим на этой окружности произвольную точку F, лежащую относительно прямой AD в другой полуплоскости, чем точки B и C.
Четырёхугольник ABDF — вписанный в окружность. Следовательно, сумма его противолежащих углов равна 180°:
Рассмотрим четырехугольник ACDF.
Отсюда следует, что четырёхугольник ABDF — вписанный.
Поскольку около треугольника ABD можно описать только одну окружность, то точка C лежит на той же окружности, что и точки A, B и D.
🔥 Видео
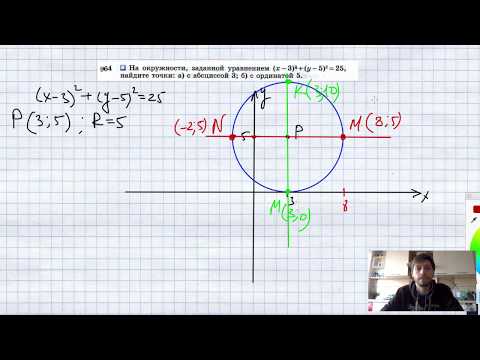
№964. На окружности, заданной уравнением (x-3)2 + + (y-5)2 = 25, найдите точки: а) с абсциссой 3;Скачать
№963. На окружности, заданной уравнением х2+у2 = 25, найдите точки: а) с абсциссой -4Скачать

№959. Начертите окружность, заданную уравнением: а) х2+у2= 9Скачать

ПРОСТОЙ СЕКРЕТ ДЛЯ НАЧИНАЮЩИХ! Реши алгебру за 12 минут — Уравнение ОкружностиСкачать

Как искать точки на тригонометрической окружности.Скачать

ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать

начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Составить уравнение окружности. Геометрия. Задачи по рисункам.Скачать

10 класс, 11 урок, Числовая окружностьСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Задача на положение точки относительно окружности(видео 55) | Подобие. Геометрия | МатематикаСкачать

№962. Даны окружность х2 + у2 = 25 и две точки А(3; 4) и В (4; -3).Скачать

ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать

№961. Окружность задана уравнением (x + 5)2 + (y-1)2= 16. Не пользуясь чертежомСкачать

№967. Напишите уравнение окружности с центром в начале координат, проходящей через точку В (-1; 3).Скачать

Как проверить лежат ли 4 точки в одной плоскости Аналитическая геометрияСкачать