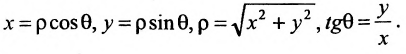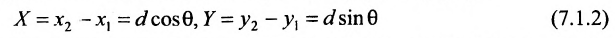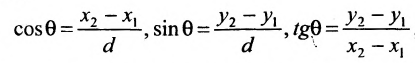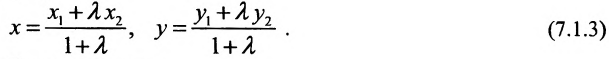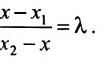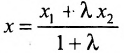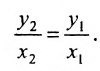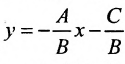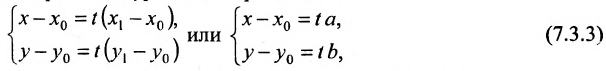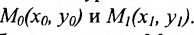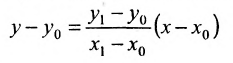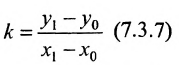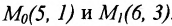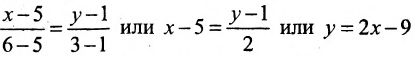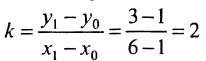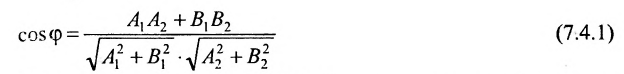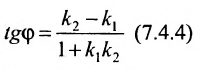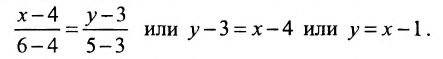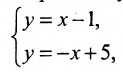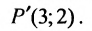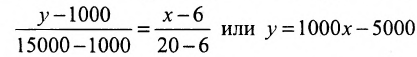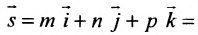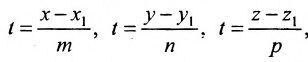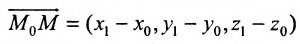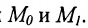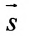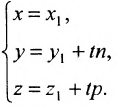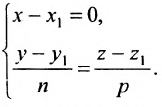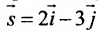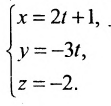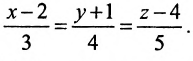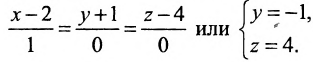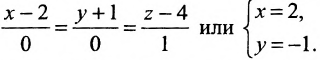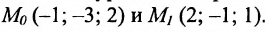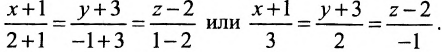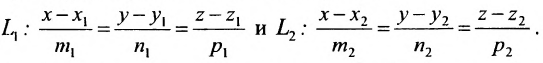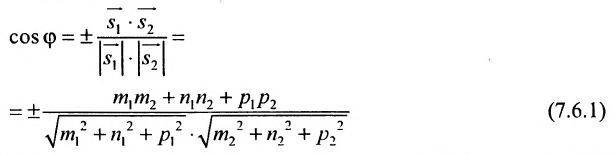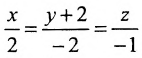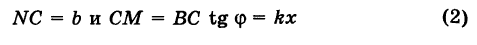Линейная функция — функция вида y=kx+b (для функций одной переменной).
- Определение и геометрический смысл
- Основное свойство линейной функции
- Задачи на прямую
- Общее уравнение прямой. Неявная линейная функция
- Система двух уравнений первой степени
- Примеры решения линейной функции
- Примеры применения линейной функции
- Прямая линия на плоскости и в пространстве с примерами решения
- Виды уравнений прямой
- Основные задачи о прямой на плоскости
- Прямая линия на плоскости и в пространстве. Системы координат на плоскости
- Основная теорема о прямой линии на плоскости
- Различные виды уравнений прямой на плоскости
- Взаимное расположение двух прямых на плоскости
- Прямая линия в пространстве
- Взаимное расположение двух прямых в пространстве
- Вычисление уравнения прямой
- Касательная к графику функции в точке. Уравнение касательной. Геометрический смысл производной
- Определения и понятия
- Геометрический смысл производной функции в точке
- Уравнение касательной прямой
- Касательная к окружности, эллипсу, гиперболе, параболе
- Касательная к окружности
- Касательная к эллипсу
- Касательная к гиперболе
- Касательная к параболе
- 📸 Видео
Видео:3. Геометрический смысл производной. Уравнение касательной и нормали.Скачать

Определение и геометрический смысл
Рассмотрим уравнение с двумя неизвестными х и у:
где 
удовлетворяют следующие пары:
Для того чтобы найти пару чисел, удовлетворяющих уравнению ( * ), нужно придать х произвольное числовое значение и подставить в уравнение ( * ), тогда у получит определенное числовое значение. Например, если х = 27, то у = 2 x 27 — 6 = 48. Очевидно, что пара чисел х =27 и у =48 удовлетворяет уравнению (*). Так же и в случае уравнения (1) можно придать х произвольное числовое значение и получить для у соответствующее числовое значение.
Так как в данном уравнении х может принимать любое числовое значение, то его называют переменной величиной. Поскольку выбор этого числового значения ничем не ограничен, то х называют независимой переменной величиной или аргументом.
Для у получаются также различные значения, но уже в зависимости от выбранного значения х; поэтому у называют зависимым переменным или функцией.
Функцию у, определяемую уравнением (1), называют линейной функцией.
Пример:
Вычислить значения линейной функции, определяемой уравнением у = 0,5х + 3,7, при следующих значениях независимого переменного: х1 = 0, х2 = —0,5, х3 = —7,6.
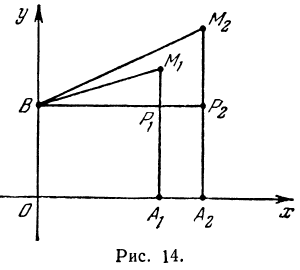
Покажем, что если принять пару чисел х и у, удовлетворяющих уравнению (1), за абсциссу и ординату точки, то геометрическим местом этих точек будет прямая линия (рис. 14).
В самом деле, рассмотрим точку В(0, b) и точки М1(х1, у1) и М2(х2, у2), координаты которых удовлетворяют уравнению (1), т. е.
Обозначим проекции точек М1 и М2 на ось Ох через А1 и A2, тогда ОА1 = х1, ОА2 = х2, А1М1= у1, А2М2 = у2. Проведем из точки В прямую, параллельную оси Ох. При этом получим b = ОВ = А1Р1 = А2Р2.
Предположим, что точки BМ1 и М2 не лежат народной прямой. Соединяя точку В с точками М1 и М2, получим два прямоугольных треугольника ВР1М1 и ВР2М2, из которых имеем:
Но так как х1, у1 и х2, у2 удовлетворяют уравнению (1), то
Выражения 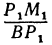
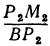








Так как М1 и М2 — произвольные точки, координаты которых удовлетворяют уравнению (1), то можно сделать следующее заключение: любая точка, координаты которой удовлетворяют уравнению (1), лежит на прямой, отсекающей на оси Оу отрезок ОВ = b и образующей с положительным направлением оси Ох угол а такой, что tg a = 
Число b называется начальной ординатой, число 
Предыдущие рассуждения позволяют сделать вывод: линейная функция y = 

Например, линейная функция 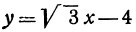
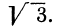
Если имеем определенную прямую, отсекающую на оси Оу отрезок b и наклоненную к оси Ох под углом 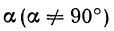
Очевидно, имеет место и такое предложение:
Всякой прямой, отсекающей на оси Оу отрезок b и наклоненной к оси Ох под углом, тангенс которого равен числу 

Координаты любой тонки, лежащей на указанной прямой, удовлетворяют уравнению (1), поэтому уравнение у = 
Отметим частные случаи.
1.Пусть b = 0, т. е. линейная функция определяется уравнением
Прямая, определяемая этим уравнением, проходит через начало координат. Здесь у пропорционален х, т. е. если х увеличить (уменьшить) в несколько раз, то и у увеличится (уменьшится) во столько же раз.
2.Пусть 
Этому уравнению соответствует прямая, параллельная оси Ох и отстоящая от нее на расстояние b.
На основании всего сказанного в этом параграфе легко решаются следующие задачи.
Задача:
Даны точки А (3, 5) и В(— 1, 4). Нужно узнать, лежат ли эти точки на прямой, уравнение которой имеет вид
Решение:
Если точка лежит на прямой, то ее координаты должны удовлетворять уравнению прямой. Поэтому для решения задачи подставим координаты точки А в уравнение (*), получим 5 = 2 x 3 — 1. Это тождество, следовательно, точка А лежит на прямой. Подставляя координаты точки В, получаем 4 = 2(— 1)—1 = —3. Отсюда видно, что точка В не лежит на прямой.
Задача:
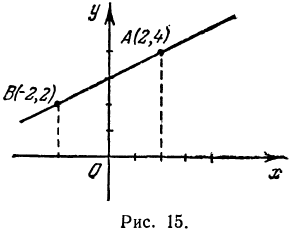
Построить прямую, уравнение которой
Решение:
Чтобы построить прямую, надо знать, например, две ее точки. Поэтому дадим х произвольное значение, например х = 2, и найдем из уравнения (**) значение
Значит, точка A (2, 4) лежит на прямой.
Это первая точка. Теперь дадим х какое-нибудь другое значение, например х = —2, и вычислим у из уравнения (**).
Точка B ( — 2, 2) лежит на прямой. Это вторая точка. Строим точки A и B (рис. 15) и проводим через них прямую, это и есть искомая прямая.
Видео:Геометрический смысл производной | КасательнаяСкачать

Основное свойство линейной функции
Рассмотрим линейную функцию у = 
Здесь первое и второе значения х различны, они отличаются друг от друга на величину х2 — х1. Величину разности х2 — х1, на которую изменяется x при переходе от x1 к х2, назовем приращением независимого переменного х. Эту величину часто будем обозначать через h, так что h = x2 — x1. Найдем, насколько изменилось значение у при изменении х1 на h . Для этого вычтем из у2 значение у1
т. е. приращение линейной функции пропорционально приращению независимого переменного.
Это и есть основное свойство линейной функции. Заметим, что х2 может быть больше, а может быть и меньше, чем х1. Поэтому h = x2 — x1 может быть как положительным, так и отрицательным числом, иначе говоря, приращение h независимого переменного может быть любого знака. То же самое относится и к приращению функции, т. е. к величине у2—у1.
Пример:
Найдем приращение функции y = 0,6x—3, если приращение независимого переменного h = 0,1.
По основному свойству у2—у1 = 0,6 x 0,1 = 0,06.
Приращение этой же функции y = 0,6x—3 , если h = —3, будет равно у2—у1 = 0,6 x (— 3) = —1,8. В этом случае приращения независимого переменного и функции отрицательны, т. е. в этом случае и независимое переменное и функция не увеличиваются, а уменьшаются.
Пример:
Найдем приращение функции у = —2x+10 при изменении х на h = —0,5. Будем иметь
Видео:Нелинейные уравнения с двумя переменными и их геометрический смысл. 9 класс.Скачать

Задачи на прямую
Задача:
Найти угол y между двумя прямыми, заданными уравнениями
Решение:
При пересечении прямых образуются четыре попарно равных угла. Найдя один из них, легко найти и другие. На рис. 16 прямые обозначены соответственно (1) и (2).
Угол хАВ является внешним по отношению к треугольнику ABC, поэтому он равен сумме двух внутренних углов треугольника, с ним не смежных, т. е.
Но углы а1 и а2 непосредственно неизвестны, а известны их тангенсы
Пример:
Найти угол между прямыми, заданными уравнениями
применяя формулу (1), получим;
Если же будем считать, что
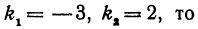
Получены два ответа: сначала найден острый угол между заданными прямыми, а затем — тупой.
Если заданы две параллельные прямые, то углы а1 и а2 равны, как соответственные, следовательно, тангенсы их тоже равны
Таким образом, мы приходим к выводу: если прямые параллельны, то их угловые коэффициенты равны.
Если прямые перпендикулярны, то угол между ними равен 90°, т. е. 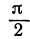
Это и есть условие перпендикулярности двух прямых. Это условие удобно запомнить в следующей формулировке: если две прямые перпендикулярны, то их угловые коэффициенты обратны по величине и противоположны по знаку.
Пример:
Найдем угол между прямыми, заданными уравнениями
Здесь угловые коэффициенты (первый равен 3, а второй 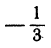
Задача:
Даны две точки: M1(x1, у1) и М2(х2, у2), где 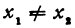
Решение:
Искомая прямая не параллельна оси Оу, поэтому ее уравнение можно написать в виде 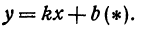

Так как прямая проходит через точки М1 и М2, то координаты этих точек должны удовлетворять уравнению ( * ), т. е.
В уравнениях ( ** ) и (*** ) все числа, кроме 

Подставляя найденные выражения в уравнение (*), получим
Это и есть уравнение прямой, проходящей через две точки, не расположенные на прямой, параллельной оси Оу.
Полученному уравнению можно придать форму, удобную для запоминания, а именно:
Задача:
Написать уравнение прямой, проходящей через данную точку М(х1,у1) и образующей с осью Ох угол а.
Решение:
Прежде всего найдем угловой коэффициент искомой прямой: он равен тангенсу угла а. Обозначим 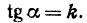
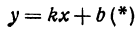
Находим отсюда неизвестное b, получим 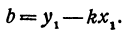
Это и есть уравнение прямой, проходящей через точку М в заданном направлении.
Если в уравнении (4) менять направление, не меняя точку M, то получим уравнение всех прямых, проходящих через заданную точку. Уравнение 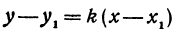

Пример:
Напишем уравнение прямой, проходящей через точку М( — 2, 3) и образующей с осью Ох угол 45°.
Так как tg 45° = 1, то угловой коэффициент равен 1; х1 = —2; у1 = 3. Уравнение прямой запишется в виде
Видео:Геометрический смысл производной. Уравнение касательнойСкачать

Общее уравнение прямой. Неявная линейная функция
Рассмотрим уравнение первой степени с двумя неизвестными
Решим его относительно у:
т. е. мы получили линейную функцию, где 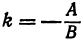
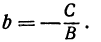
Координаты любой точки, лежащей на этой прямой, удовлетворяют уравнению (1), поэтому будем называть его также уравнением прямой.
Рассмотрим особо случай, когда B = 0, так как на нуль делить нельзя.
Уравнение (1) примет вид
Поэтому, каков бы ни был у, х всегда равен 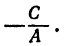
Таким образом, любому уравнению первой степени соответствует некоторая прямая. Придавая в уравнении (1) коэффициентам А, В и С различные значения, можно получить любое уравнение первой степени. Поэтому уравнение (1) называют общим уравнением прямой.
Из уравнения (1) (если 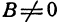
Видео:2. Определение производной. Геометрический и физический смысл производной.Скачать

Система двух уравнений первой степени
Напомним, что две прямые, расположенные на плоскости, могут или пересекаться, или быть параллельными (т. е. не пересекаться), или сливаться (в этом случае можно сказать, что они пересекаются в каждой своей точке).
Рассмотрим систему двух уравнений
Каждое из этих уравнений является уравнением прямой. Решить систему — это значит найти значения х и у, которые удовлетворяют и первому и второму уравнениям. Но так как х и у определяют точку, то следовательно, решить систему—это значит найти точку, лежащую и на первой и на второй прямых, т. е. найти точку пересечения прямых.
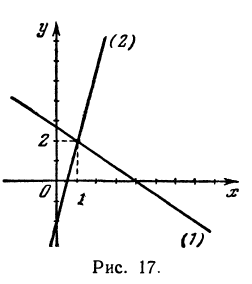
Пример:
Найдем точку пересечения двух прямых:
Решая эту систему, получим: х = 1, у = 2, т. е. прямые пересекаются в точке (1,2) (рис. 17).
Пример:
Найдем точку пересечения двух прямых:
Решая эту систему, получим:
Последнее равенство нелепо, значит, прямые не пересекаются, Рис. 17. т. е. они параллельны.
Пример:
Найдем точку пересечения данных прямых
Решая эту систему, получим:
Полученное равенство всегда справедливо, т. е. справедливо при любом значении x. Это значит, что две прямые пересекаются в каждой своей точке, что может быть только тогда, когда они сливаются.
Заметим, что два уравнения, рассматриваемые в этом примере, являются равносильными, поэтому они и представляют одну и ту же прямую.
Видео:Математика без Ху!ни. Уравнение касательной.Скачать

Примеры решения линейной функции
Линейная функция встречается в формулировках многих физических законов и технических задач. Приведем примеры.
Пример:
Если точка движется равномерно по прямой, то ее расстояние от выбранной точки (от начала координат) выражается при помощи уравнения
где — начальное расстояние, v0 — скорость, t — время; это, как мы уже знаем, есть линейная функция.
Пример:
Закон Ома записывается в виде
где v — напряжение, R — сопротивление и I — ток. Если не изменяется, то v является линейной функцией тока I .
Пример:
Если стоимость провоза единицы товара по железной дороге равна а руб. за километр, то стоимость v провоза N единиц товара на l км равна
Если же стоимость товара на месте равна М руб., то после перевозки за него надо заплатить
Здесь v—линейная функция l.
Линейная функция встречается в различных областях, но, где бы она ни встречалась, ее всегда можно рассматривать как уравнение прямой. Этим обстоятельством часто пользуются при решении задач.
Задача:
Два города А и В, расстояние между которыми равно 300 км, находятся на одной железнодорожной магистрали. На этой же магистрали между городами А и В надо выбрать пункт С, в котором предполагается устроить склад нефти для снабжения указанных городов. Надо выбрать пункт С так, чтобы общая стоимость перевозок нефти для снабжения города А и города В была наименьшей. Известно, что город А потребляет 400 т нефти, а город В—200 т. Перевозка одной тонны нефти на один километр обходится в а руб.
Решение:
Обозначим расстояние от А до предполагаемого пункта С через х. Тогда расстояние от города В до С равно 300 — х. Стоимость перевозки одной тонны нефти из С в A равна ах руб., а перевозки 400 т—400аx руб. Аналогично перевозка нефти из С в В будет стоить 200а (300 — х) руб. Стоимость всех перевозок, которую обозначим через у, будет выражаться так:
Это линейная функция. Если примем х за абсциссу, а у за ординату точки, то полученная линейная функция определяет уравнение некоторой прямой. Угловой коэффициент ее равен 200а, т. е. положителен, следовательно, эта прямая образует с осью Ох острый угол и поэтому с увеличением независимого переменного поднимается вверх. По смыслу задачи величина х заключена между 0 и 300, т. е. 
Так как пункт С надо выбрать так, чтобы стоимость была наименьшей, то его следует расположить в городе A, если же этого сделать нельзя по каким-либо соображениям, то, чем ближе расположить его к A, тем выгодней.
Видео:22. Дифференциал функции и его геометрический смыслСкачать

Примеры применения линейной функции




Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:Урок 320. Производная функции и ее геометрический смыслСкачать

Прямая линия на плоскости и в пространстве с примерами решения
Содержание:
Общее уравнение прямой:
Пусть на плоскости дана декартова система координат. Движение точки с произвольными координатами х и у по этой плоскости порождает линию.
Определение: Любое соотношение
Определение: Порядок линии определяется по высшему показателю степени переменных х и у или по сумме показателей степени в произведении этих величин.
Пример:
а) 2х + Зу-5 = 0 — линия первого порядка; точка A(l; 1) удовлетворяет этому соотношению, а точка, например, В(1; 0) — ему не удовлетворяет;
б)
в) 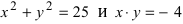
Рассмотрим другое определение линии:
Определение: Геометрическое место точек, координаты которых удовлетворяют уравнению F(x; у)=0, называется линией, а само уравнение F(x; у) = 0 — уравнением линии.
Определение: Общим уравнением прямой называется уравнение первого порядка вида
Рассмотрим частные случаи этого уравнения:
а) С = 0; 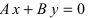
Рис. 20. Прямая, проходящая через начало координат.
б) 5 = 0; Ах+С=0 — прямая проходит параллельно оси ординат Оу (Рис. 21):
Рис. 21. Прямая, проходящая параллельно оси ординат Оу.
в) А = 0; Ву+С=0 — прямая проходит параллельно оси абсцисс Ох (Рис. 22):
Рис. 22. Прямая, проходящая параллельно оси абсцисс Ох.
Видео:Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Виды уравнений прямой
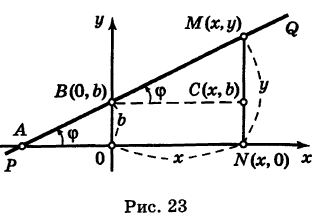
1. Уравнение прямой с угловым коэффициентом. Пусть дано общее уравнение прямой 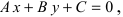
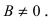
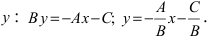
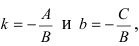
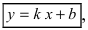
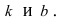
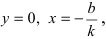
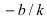
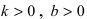
Рис. 23. Отрезки, отсекаемые прямой на координатных осях.
Из рисунка видно, что 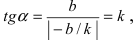
2. Уравнение прямой в отрезках.
Пусть в общем уравнении прямой параметр 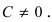
Обозначим через 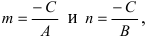
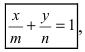
Рис. 24. Отрезки, отсекаемые прямой на координатных осях.
При у=о, х=m, т.е. прямая отсекает на оси абсцисс отрезок m. Следовательно, прямая проходит через 2 точки:
3. Уравнение прямой, проходящей через две заданные точки. Пусть дано общее уравнение прямой Ах + Ву + С = 0, которая проходит через две известные точки 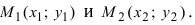
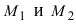
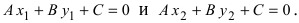
Пусть 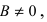
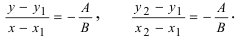
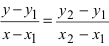
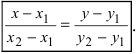
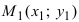
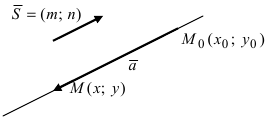
4. Уравнение прямой, проходящей через заданную точку 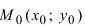
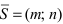
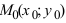
Определение: Вектор 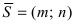
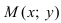
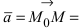
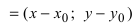
Рис. 25. Прямая, проходящая через данную точку параллельно направляющему вектору.
В силу того, что вектора 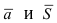
Определение: Полученное уравнение называется либо уравнением, проходящим через заданную точку параллельно направляющему вектору, либо каноническим уравнением прямой.
5. Параметрическое уравнение прямой. Если каждую дробь в каноническом уравнении прямой приравнять некоторому параметру t, то получим параметрическое уравнение прямой
Основные задачи о прямой на плоскости
1. Координаты точки пересечения двух прямых. Пусть две прямые заданы общими уравнениями 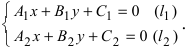
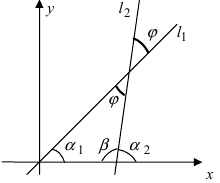
2. Угол между двумя пересекающимися прямыми. Пусть даны две пересекающиеся прямые, заданные уравнениями с угловыми коэффициентами
Требуется найти угол между этими прямыми (Рис. 26):
Рис. 26. Угол между двумя прямыми.
Из рисунка видно, что 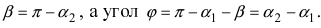
Наименьший угол между пересекающимися прямыми определим формулой 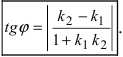
- а) если прямые
параллельны или совпадают
то
Отсюда следует условие параллельности прямых: угловые коэффициенты прямых равны между собой
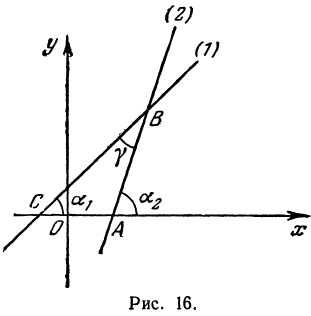
- б) если прямые
перпендикулярны
то
не существует.
Отсюда следует условие перпендикулярности прямых: угловые коэффициенты прямых связаны между собой соотношением
Пример:
Определить угол между прямыми
Решение:
В силу того, что 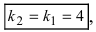
Пример:
Выяснить взаимное расположение прямых
Решение:
Так как угловые коэффициенты 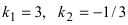
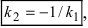
3. Расстояние от точки до прямой. Расстояние от точки до прямой определятся вдоль перпендикуляра, опущенного из точки 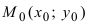
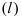
Если прямая 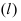
Видео:Геометрический смысл дифференциального уравненияСкачать

Прямая линия на плоскости и в пространстве. Системы координат на плоскости
Рассмотрим произвольную прямую. Выберем на этой прямой начальную точку, обозначаемую буквой О, определим положительное направление, выберем некоторый отрезок в качестве линейной единицы, благодаря чему прямая станет осью. После этого условимся называть координатой любой точки М на этой оси величину отрезка 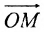
Декартова прямоугольная система координат определяется заданием линейной единицы для измерения длин и двух взаимно перпендикулярных осей, занумерованных в каком-нибудь порядке, т.е. указано, какая из них считается первой, а какая — второй. Точка пересечения осей называется началом координат и обозначается через О, а сами оси — координатными осями, причем первую из них называют также осью абсцисс и обозначают через Ох, а вторую — осью ординат, обозначаемую Оу.
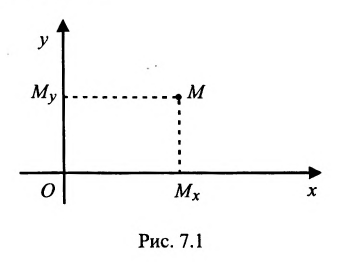
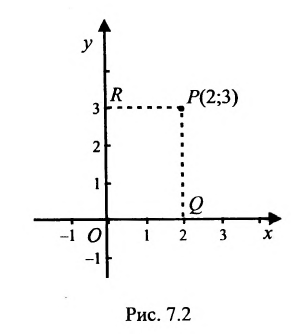
Пусть М- произвольная точка плоскости. Спроектируем точку M на координатные оси, т.е., проведем через М перпендикуляры к осям Ох и Оу; основания этих перпендикуляров обозначим соответственно 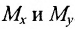
Координатами точки М в заданной системе называются числа 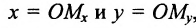
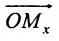
Если задана декартова прямоугольная система координат, то каждая точка М плоскости в этой системе имеет одну вполне определенную пару координат х, у — М(х, у). И обратно, для любых х и у на плоскости найдется одна вполне определенная точка с абсциссой х и ординатой у.
На рис. 7.2 положение точки Р полностью определяется ее координатами (2;3).
Две координатные оси разделяют всю плоскость на четыре части, называемыми координатными плоскостями, определяемыми соответственно:
- первая координатная четверть: х>0, у>0;
- вторая координатная четверть: х
0, у>0;
- третья координатная четверть: х
0, у
0;
- четвертая координатная четверть: х>0, у
0.
Декартова прямоугольная система координат является наиболее употребительной. Однако, в отдельных случаях могут оказаться более удобными или косоугольная декартова или полярная системы координат.
Косоугольная система координат от прямоугольной декартовой системы координат отличается только произвольным углом между осями координат.
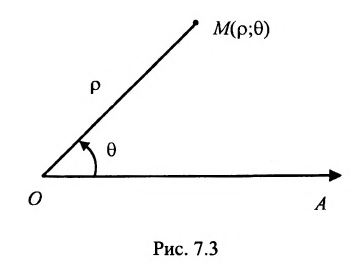
Полярная система координат определяется заданием некоторой точки О, называемой полюсом, исходящего из этой точки луча OA, называемого полярной осью, масштаба для измерения длин и направления- вращения в плоскости, считаемого положительным (рис. 7.3).
Каждая точка М в полярной системе координат задается парой координат 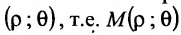
Декартова прямоугольная система координат связана с полярной системой формулами:
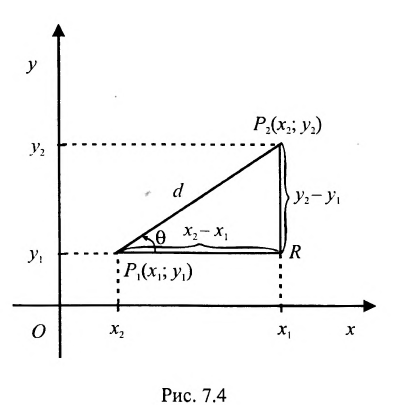
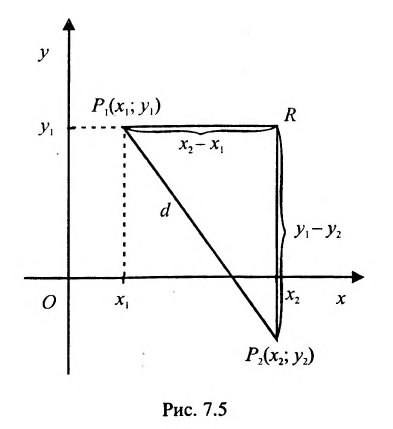
Основным инструментом аналитической геометрии служит формула для вычисления расстояния между двумя точками
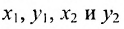
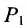
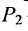
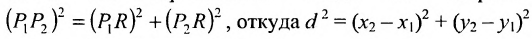
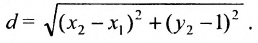
Это и есть формула для вычисления расстояния между двумя точками.
Важно иметь в виду, что эта формула остается в силе независимо от того, как расположены точки 
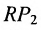
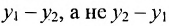
Расстояние между точками, вычисляемое по формуле (7.1.1), от этого не изменится, так как 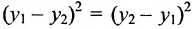
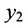
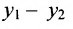
Если обозначить через 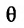
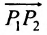
выражают проекции произвольного отрезка на координатные оси через его длину и полярный угол. Из формул (7.1.2) получаем формулы:
позволяющие определить полярный угол отрезка по координатам его конца и начала. Кроме того, если u — произвольная ось, а 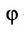
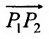
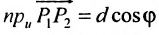
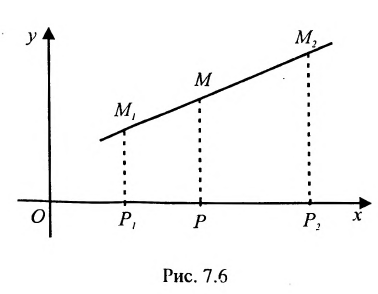
Пусть на плоскости даны две произвольные точки, из которых одна считается первой, другая — второй. Обозначим их в заданном порядке через 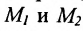
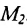
Определение 7.1.1. Число 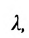
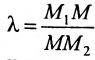
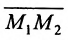
Число 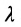
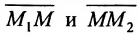
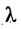
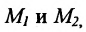
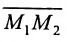
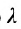
Задача о делении отрезка в данном отношении формулируется следующим образом:
Считая известными координаты двух точек 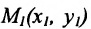
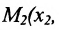
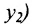
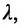
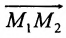
Решение задачи определяется следующей теоремой.
Теорема 7.1.1. Если точка М(х, у) делит направленный отрезок 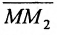
Доказательство:
Спроектируем точки 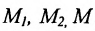
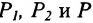
Подставив в (7.1.4) величины отрезков 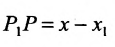
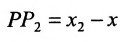
Разрешая это уравнение относительно х, находим:
Вторая формула (7.1.3) получается аналогично.
Если 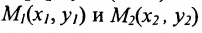
середина отрезка 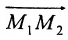
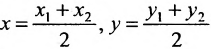
получаются из (7.1.3) при 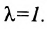
Основная теорема о прямой линии на плоскости
Предположим, что в данной плоскости задана прямоугольная система координат и некоторая прямая l.
Всякий ненулевой вектор, коллинеарный данной прямой, называется её направляющим вектором. Всякие два направляющих вектора 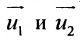
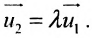
Для всех направляющих векторов 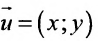
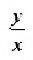
Действительно, если 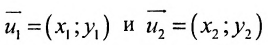
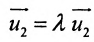
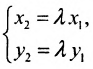
Угловой коэффициент прямой можно определить и по-другому: как тангенс угла, образованного положительным направлением оси абсцисс и заданной прямой.
Справедлива следующая теорема.
Теорема 7.3,1. Всякая прямая на плоскости определяется уравнением первой степени с двумя переменными х и у; и обратно, всякое уравнение первой степени с двумя переменными х и у определяет некоторую прямую на плоскости.
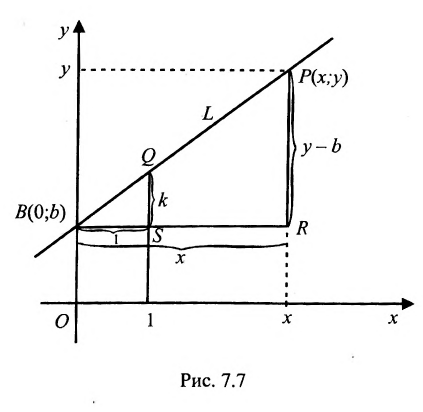
Доказательство: Пусть В = (О,b>- точка пересечения прямой L с осью у, а Р = (х,у) — любая другая точка на этой прямой. Проведем через точку В прямую, параллельную оси х, а через точку Р — прямую, параллельную оси у; проведем также прямую х = 1. Пусть k -угловой коэффициент прямой L (см. рис. 7.7). Случай к =0 не исключается.
Так как треугольники BSQ и BRP подобны, то 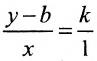
Следовательно, если точка Р принадлежит прямой L, то ее координаты удовлетворяют уравнению (7.2.1). Обратно, нетрудно показать, что если х и у связаны уравнением (7.2.1), то точка Р принадлежит прямой L, проходящей через точку (0;b) и имеющей угловой коэффициент k.
Таким образом, уравнение любой прямой можно записать в виде:
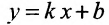
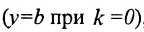
В обоих случаях мы получаем уравнение первой степени. Кроме того, каждое уравнение первой степени ио х и у можно привести к виду (7.2.2) либо (7.2.3).
Докажем обратное утверждение. Предположим, что задано произвольное уравнение первой степени:
Если 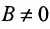
т.е. в виде (7.2.2). При В = 0 уравнение (7.2.3) сводится к уравнению
или 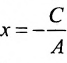
Таким образом, любая прямая описывается уравнением первой степени с неизвестными х и у, и обратно, каждое уравнение первой степени с неизвестными х и v определяет некоторую прямую.
Уравнение (7.2.4) называется общим уравнением прямой. Так
как 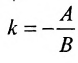
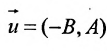
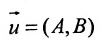
1. 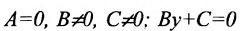
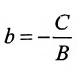
2. 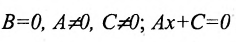
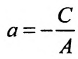
3. 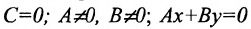
4. А=0; С=0; Ву-0 или у = 0 — это уравнение оси абсцисс Ох.
5. В=0;С=0; Ах=0 или х = 0 — это уравнение оси ординат Оу.
Различные виды уравнений прямой на плоскости
Положение прямой на плоскости относительно системы координат можно задать различными способами. Например, прямая однозначно определяется: двумя различными точками; точкой и направляющим вектором; отрезками, отсекаемыми прямой на осях координат и др. Однако, обязательно, должна быть точка, лежащая на этой прямой.
Пусть в уравнении (7.2.4) ни один из коэффициентов А, В, С не равен нулю. Перенесем свободные члены вправо и разделим на (-С). Получим уравнение прямой в отрезках:
где 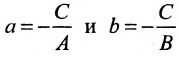
Рассмотрим прямую l на плоскости и выберем на этой прямой какие-нибудь точки 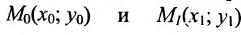
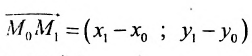
Геометрическое место концов всевозможных векторов вида 
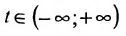
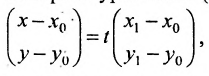
где 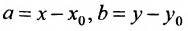
Система (7.3.3) равносильна уравнению
называемым каноническим уравнением прямой на плоскости. Из системы (7.3.3) можно получить уравнение
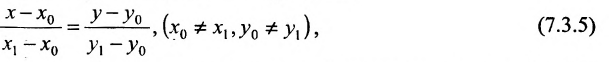
Если абсциссы точек 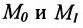

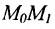
Если ординаты точек 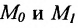
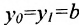
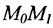
угловой коэффициент прямой.
Уравнение (7.3.6) называется уравнением прямой, проходящей через точку 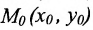
Пример:
Составить уравнение прямой, проходящей через две точки
Решение:
I способ. Воспользуемся уравнением (7.3.5). Подставив известные координаты точек 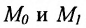
II способ. Зная координаты точек 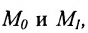
Тогда, воспользовавшись уравнением (7.3.6), найдём искомое уравнение прямой: 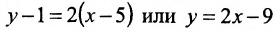
Заметим, что составленное уравнение можно записать как уравнение прямой в отрезках, разделив все члены уравнения
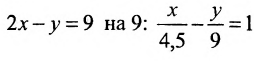
Взаимное расположение двух прямых на плоскости
Пусть на плоскости заданы две прямые общими уравнениями 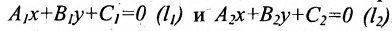
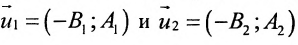
Если прямые параллельны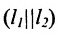
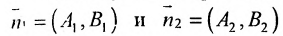
И обратно, если координаты при неизвестных х и у пропорциональны, то прямые параллельны. Следовательно, можно сформулировать следующую теорему:
Теорема 7.4.1. Две прямые 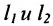
Например, прямые 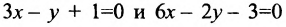
т. к.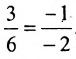
Если прямые перпендикулярны 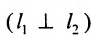
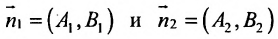
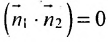
Справедливо и обратное утверждение: если скалярное произведение нормальных векторов равно нулю, то прямые /, и /2 перпендикулярны.
Теорема 7.4.2. Две прямые 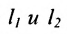
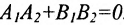
Например, прямые 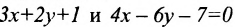
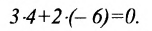
Если прямые заданы уравнениями вида 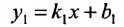
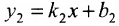
Для того чтобы прямые были параллельны, необходимо и достаточно, чтобы выполнялось равенство
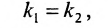
а для их перпендикулярности необходимо и достаточно, чтобы
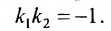
Пример:
Найти проекцию точки Р (2, 3) на прямую, проходящую через точки А (4, 3) и В (6, 5).
Решение:
Проекция точки Р на прямую АВ — это точка пересечения перпендикуляра, проведенного к этой прямой из точки Р.
Вначале составим уравнение прямой АВ. Воспользовавшись уравнением (7.3.5), последовательно получаем:
Для того, чтобы составить уравнение перпендикуляра, проведенного из точки Р на прямую АВ, воспользуемся уравнением (7.3.6). Угловой коэффициент k определим из условия перпендикулярности двух прямых, т. е. из формулы (7.4.6). Поскольку 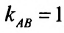
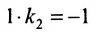
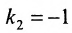
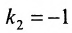
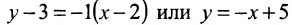
Решая систему уравнений, составленную из уравнений прямой АВ и перпендикуляра
найдём координаты проекции точки Р на прямую АВ: х=3 у=2, т.е.
Пример:
Издержки на производство шести автомобилей составляют 1000 млн. ден. ед., а на производство двадцати автомобилей- 15000 млн. ден. ед. Определить издержки на производство 22 автомобилей при условии, что функция К(х) издержек производства линейна, т.е. имеет вид у = ах + b .
Решение:
Обозначим через х количество автомобилей, а через y- издержки производства. Тогда из условия задачи следует, что заданы координаты двух точек- А(6; 1000) и В(20; 15000), принадлежащих линейной функции у = ах +b. Воспользовавшись уравнением (7.3.6 ), найдём искомое уравнение:
Подставив в найденную функцию х = 22, определим издержки на производство 22 автомобилей:
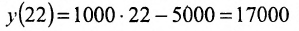
Пример:
Фирма продаёт свои изделия по 10 ден. ед. за единицу. Затраты на изготовление одного изделия составляют 6 ден. ед. Непроизводственные расходы фирмы равны 300 ден. ед. в год. Определить годовой выпуск продукции, необходимой для того, чтобы фирма работала с прибылью.
Решение:
Обозначим через х объём произведенной продукции. Тогда доход фирмы равен D = 10x. Затраты на производство определяются уравнением: 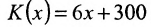
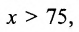
Прямая линия в пространстве
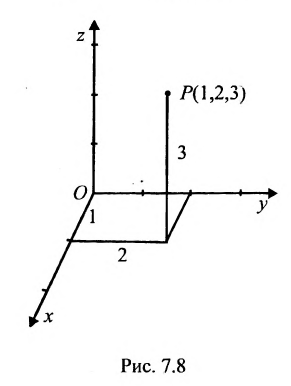
Системы координат в пространстве
В трехмерном пространстве система координат определяется тремя взаимно перпендикулярными осями, проходящими через начало координат О. Снабдив каждую ось единицей измерения длин, можно задать тремя упорядоченными числами (называемыми координатами) положение точки в пространстве. Например, точка Р задается упорядоченной тройкой чисел Р( 1,2,3).
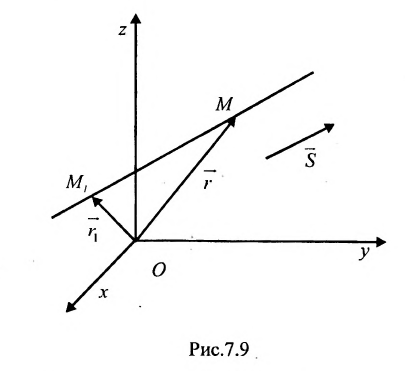
Пусть задано пространство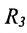
Положение прямой в пространстве вполне определяется заданием какой-либо сё фиксированной точки 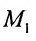
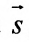
Вектор 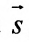
Итак, пусть прямая L проходит через точку 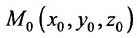
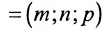
Рассмотрим произвольную точку M(x,y,z) на этой прямой. Из рисунка видно, что вектор 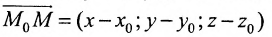
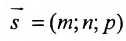
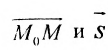
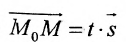
Уравнение 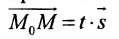
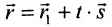
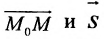
Полученные уравнения называются параметрическими уравнениями прямой.
При изменении параметра t изменяются координаты х, у и z и точка М перемещается по прямой.
Разрешив уравнения (7.5.2) относительно t
и приравняв найденные значенияt получим канонические уравнения прямой:
Если прямая L в пространстве задается двумя своими точками 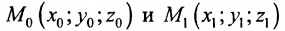
можно взять в качестве направляющего вектора и тогда уравнения (7.5.3) преобразуются в уравнения
где 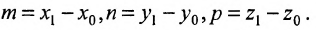
Пример:
Составить параметрические уравнения прямой, проходящей через точку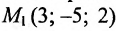
Решение:
В качестве направляющего вектора 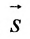
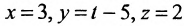
Пример:
Записать уравнения прямой 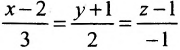
Обозначим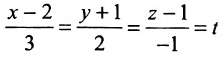
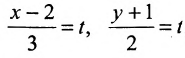
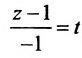
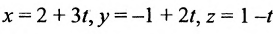
Замечание. Пусть прямая перпендикулярна одной из координатных осей, например, оси Ох. Тогда направляющий вектор
прямой перпендикулярный оси Ох, имеет координаты (о; n; р) и параметрические уравнения прямой примут вид
Исключая из уравнений параметр t, получим уравнения прямой в виде
Однако и в этом случае формально можно записывать канонические уравнения прямой в виде 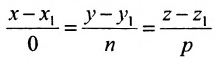
Аналогично, канонические уравнения
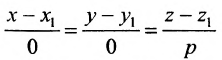
Пример:
Составить канонические и параметрические уравнения прямой, проходящей через точку 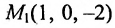
Решение:
Подставив координаты точки 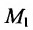
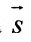
.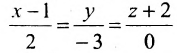
Пример:
Составить канонические уравнения прямой, проходящей через точку М(2, -1,4) параллельно
а) прямой 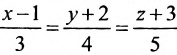
Решение:
а) Поскольку направляющий вектор заданной прямой
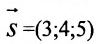
подставив координаты точки М(2; -1; 4) и вектора 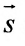
б) Поскольку единичный вектор оси О х: 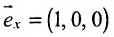
(7.5.3) координаты точки М(2; -1; 4 ) и вектора 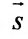
в) В качестве направляющего вектора 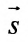
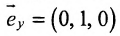
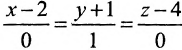
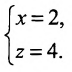
г) Единичный вектор оси Oz : 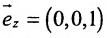
Пример:
Составить уравнение прямой, проходящей через две заданные точки
Решение:
Подставив координаты точек 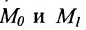
(7.5.4), получим:
Взаимное расположение двух прямых в пространстве
Углом между прямыми в пространстве будем называть любой из смежных углов, образованных двумя прямыми, проведенными через произвольную точку параллельно данным. Пусть в пространстве заданы две прямые:
Очевидно, что за угол 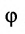
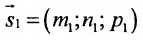
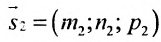
Условия параллельности и перпендикулярности двух прямых равносильны условиям параллельности и перпендикулярности их направляющих векторов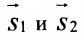
Две прямые параллельны тогда и только тогда, когда пропорциональны соответствующие координаты направляющих векторов:
т.е. 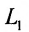
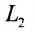
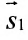
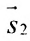
Две прямые перпендикулярны тогда и только тогда, когда сумма произведений соответствующих координат направляющих векторов равна нулю:
Пример:
Найти угол между прямыми 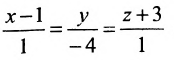
Решение:
Воспользуемся формулой (7.6.1), в которую подставим координаты направляющих векторов 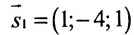
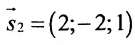
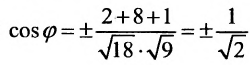
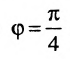
Видео:АЛГЕБРА С НУЛЯ — Что такое Производная?Скачать

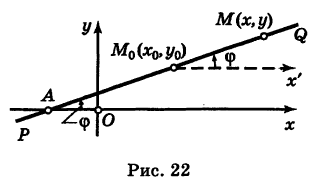
Вычисление уравнения прямой
Пусть PQ — некоторая прямая на плоскости Оху (рис. 22). Через произвольную точку М0 (х0, у0) этой прямой (условно называемую «начальной точкой») проведем прямую М0х параллельную оси Ох и имеющую с ней одинаковое направление. Тогда наименьший неотрицательный угол 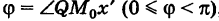
Очевидно, этот угол не зависит от выбора точки М0. Если прямая PQ пересекает ось Ох в некоторой точке А (а, 0), то ф есть обычный угол между направленными прямыми. Если PQ || Ох, то, очевидно, Ф = 0. Начальная точка М0 прямой и угол ф («направление прямой») однозначно определяют положение этой прямой на плоскости.
1) Пусть сначала 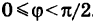
Ордината у = NM текущей точки М (х, у) прямой (рис. 23) состоит из двух частей:
из них первая постоянна, а вторая переменна. Введя угловой коэффициент tg ф = k9 из рис. 23 будем иметь
Нетрудно проверить, что формула (3) остается справедливой также и при х
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:10 класс, 43 урок, Уравнение касательной к графику функцииСкачать

Касательная к графику функции в точке. Уравнение касательной. Геометрический смысл производной
Статья дает подробное разъяснение определений, геометрического смысла производной с графическими обозначениями. Будет рассмотрено уравнение касательной прямой с приведением примеров, найдено уравнения касательной к кривым 2 порядка.
Видео:✓ Касательная. Геометрический смысл производной и дифференциала | матан #033 | Борис ТрушинСкачать

Определения и понятия
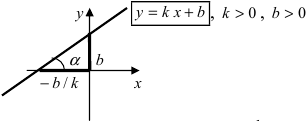
Угол наклона прямой y = k x + b называется угол α , который отсчитывается от положительного направления оси о х к прямой y = k x + b в положительном направлении.
На рисунке направление о х обозначается при помощи зеленой стрелки и в виде зеленой дуги, а угол наклона при помощи красной дуги. Синяя линия относится к прямой.
Угловой коэффициент прямой y = k x + b называют числовым коэффициентом k .
Угловой коэффициент равняется тангенсу наклона прямой, иначе говоря k = t g α .
- Угол наклона прямой равняется 0 только при параллельности о х и угловом коэффициенте, равному нулю, потому как тангенс нуля равен 0 . Значит, вид уравнения будет y = b .
- Если угол наклона прямой y = k x + b острый, тогда выполняются условия 0 α π 2 или 0 ° α 90 ° . Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию t g α > 0 , причем имеется возрастание графика.
- Если α = π 2 , тогда расположение прямой перпендикулярно о х . Равенство задается при помощи равенства x = c со значением с , являющимся действительным числом.
- Если угол наклона прямой y = k x + b тупой, то соответствует условиям π 2 α π или 90 ° α 180 ° , значение углового коэффициента k принимает отрицательное значение, а график убывает.
Определение 3
Секущей называют прямую, которая проходит через 2 точки функции f ( x ) . Иначе говоря, секущая – это прямая, которая проводится через любые две точки графика заданной функции.
По рисунку видно, что А В является секущей, а f ( x ) – черная кривая, α — красная дуга, означающая угол наклона секущей.
Когда угловой коэффициент прямой равняется тангенсу угла наклона, то видно, что тангенс из прямоугольного треугольника А В С можно найти по отношению противолежащего катета к прилежащему.
Получаем формулу для нахождения секущей вида:
k = t g α = B C A C = f ( x B ) — f x A x B — x A , где абсциссами точек А и В являются значения x A , x B , а f ( x A ) , f ( x B ) — это значения функции в этих точках.
Очевидно, что угловой коэффициент секущей определен при помощи равенства k = f ( x B ) — f ( x A ) x B — x A или k = f ( x A ) — f ( x B ) x A — x B , причем уравнение необходимо записать как y = f ( x B ) — f ( x A ) x B — x A · x — x A + f ( x A ) или
y = f ( x A ) — f ( x B ) x A — x B · x — x B + f ( x B ) .
Секущая делит график визуально на 3 части: слева от точки А , от А до В , справа от В . На располагаемом ниже рисунке видно, что имеются три секущие, которые считаются совпадающими, то есть задаются при помощи аналогичного уравнения.
По определению видно, что прямая и ее секущая в данном случае совпадают.
Секущая может множественно раз пересекать график заданной функции. Если имеется уравнение вида у = 0 для секущей, тогда количество точек пересечения с синусоидой бесконечно.
Касательная к графику функции f ( x ) в точке x 0 ; f ( x 0 ) называется прямая, проходящая через заданную точку x 0 ; f ( x 0 ) , с наличием отрезка, который имеет множество значений х , близких к x 0 .
Рассмотрим подробно на ниже приведенном примере. Тогда видно, что прямая, заданная функцией y = x + 1 , считается касательной к y = 2 x в точке с координатами ( 1 ; 2 ) . Для наглядности, необходимо рассмотреть графики с приближенными к ( 1 ; 2 ) значениями. Функция y = 2 x обозначена черным цветом, синяя линия – касательная, красная точка – точка пересечения.
Очевидно, что y = 2 x сливается с прямой у = х + 1 .
Для определения касательной следует рассмотреть поведение касательной А В при бесконечном приближении точки В к точке А . Для наглядности приведем рисунок.
Секущая А В , обозначенная при помощи синей линии, стремится к положению самой касательной, а угол наклона секущей α начнет стремиться к углу наклона самой касательной α x .
Касательной к графику функции y = f ( x ) в точке А считается предельное положение секущей А В при В стремящейся к А , то есть B → A .
Теперь перейдем к рассмотрению геометрического смысла производной функции в точке.
Видео:Что такое касательная | Осторожно, спойлер! | Борис Трушин |Скачать

Геометрический смысл производной функции в точке
Перейдем к рассмотрению секущей А В для функции f ( x ) , где А и В с координатами x 0 , f ( x 0 ) и x 0 + ∆ x , f ( x 0 + ∆ x ) , а ∆ x обозначаем как приращение аргумента. Теперь функция примет вид ∆ y = ∆ f ( x ) = f ( x 0 + ∆ x ) — f ( ∆ x ) . Для наглядности приведем в пример рисунок.
Рассмотрим полученный прямоугольный треугольник А В С . Используем определение тангенса для решения, то есть получим отношение ∆ y ∆ x = t g α . Из определения касательной следует, что lim ∆ x → 0 ∆ y ∆ x = t g α x . По правилу производной в точке имеем, что производную f ( x ) в точке x 0 называют пределом отношений приращения функции к приращению аргумента, где ∆ x → 0 , тогда обозначим как f ( x 0 ) = lim ∆ x → 0 ∆ y ∆ x .
Отсюда следует, что f ‘ ( x 0 ) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x , где k x обозначают в качестве углового коэффициента касательной.
То есть получаем, что f ’ ( x ) может существовать в точке x 0 причем как и касательная к заданному графику функции в точке касания равной x 0 , f 0 ( x 0 ) , где значение углового коэффициента касательной в точке равняется производной в точке x 0 . Тогда получаем, что k x = f ‘ ( x 0 ) .
Геометрический смысл производной функции в точке в том, что дается понятие существования касательной к графику в этой же точке.
Видео:Производная: секретные методы решения. Готовимся к ЕГЭ | Математика TutorOnlineСкачать

Уравнение касательной прямой
Чтобы записать уравнение любой прямой на плоскости, необходимо иметь угловой коэффициент с точкой, через которую она проходит. Его обозначение принимается как x 0 при пересечении.
Уравнение касательной к графику функции y = f ( x ) в точке x 0 , f 0 ( x 0 ) принимает вид y = f ‘ ( x 0 ) · x — x 0 + f ( x 0 ) .
Имеется в виду, что конечным значением производной f ‘ ( x 0 ) можно определить положение касательной, то есть вертикально при условии lim x → x 0 + 0 f ‘ ( x ) = ∞ и lim x → x 0 — 0 f ‘ ( x ) = ∞ или отсутствие вовсе при условии lim x → x 0 + 0 f ‘ ( x ) ≠ lim x → x 0 — 0 f ‘ ( x ) .
Расположение касательной зависит от значения ее углового коэффициента k x = f ‘ ( x 0 ) . При параллельности к оси о х получаем, что k k = 0 , при параллельности к о у — k x = ∞ , причем вид уравнения касательной x = x 0 возрастает при k x > 0 , убывает при k x 0 .
Произвести составление уравнения касательной к графику функции y = e x + 1 + x 3 3 — 6 — 3 3 x — 17 — 3 3 в точке с координатами ( 1 ; 3 ) с определением угла наклона.
Решение
По условию имеем, что функция определяется для всех действительных чисел. Получаем, что точка с координатами, заданными по условию, ( 1 ; 3 ) является точкой касания, тогда x 0 = — 1 , f ( x 0 ) = — 3 .
Необходимо найти производную в точке со значением — 1 . Получаем, что
y ‘ = e x + 1 + x 3 3 — 6 — 3 3 x — 17 — 3 3 ‘ = = e x + 1 ‘ + x 3 3 ‘ — 6 — 3 3 x ‘ — 17 — 3 3 ‘ = e x + 1 + x 2 — 6 — 3 3 y ‘ ( x 0 ) = y ‘ ( — 1 ) = e — 1 + 1 + — 1 2 — 6 — 3 3 = 3 3
Значение f ’ ( x ) в точке касания является угловым коэффициентом касательной, который равняется тангенсу наклона.
Тогда k x = t g α x = y ‘ ( x 0 ) = 3 3
Отсюда следует, что α x = a r c t g 3 3 = π 6
Ответ: уравнение касательной приобретает вид
y = f ‘ ( x 0 ) · x — x 0 + f ( x 0 ) y = 3 3 ( x + 1 ) — 3 y = 3 3 x — 9 — 3 3
Для наглядности приведем пример в графической иллюстрации.
Черный цвет используется для графика исходной функции, синий цвет – изображение касательной, красная точка – точка касания. Рисунок, располагаемый справа, показывает в увеличенном виде.
Выяснить наличие существования касательной к графику заданной функции
y = 3 · x — 1 5 + 1 в точке с координатами ( 1 ; 1 ) . Составить уравнение и определить угол наклона.
Решение
По условию имеем, что областью определения заданной функции считается множество всех действительных чисел.
Перейдем к нахождению производной
y ‘ = 3 · x — 1 5 + 1 ‘ = 3 · 1 5 · ( x — 1 ) 1 5 — 1 = 3 5 · 1 ( x — 1 ) 4 5
Если x 0 = 1 , тогда f ’ ( x ) не определена, но пределы записываются как lim x → 1 + 0 3 5 · 1 ( x — 1 ) 4 5 = 3 5 · 1 ( + 0 ) 4 5 = 3 5 · 1 + 0 = + ∞ и lim x → 1 — 0 3 5 · 1 ( x — 1 ) 4 5 = 3 5 · 1 ( — 0 ) 4 5 = 3 5 · 1 + 0 = + ∞ , что означает существование вертикальной касательной в точке ( 1 ; 1 ) .
Ответ: уравнение примет вид х = 1 , где угол наклона будет равен π 2 .
Для наглядности изобразим графически.
Найти точки графика функции y = 1 15 x + 2 3 — 4 5 x 2 — 16 5 x — 26 5 + 3 x + 2 , где
- Касательная не существует;
- Касательная располагается параллельно о х ;
- Касательная параллельна прямой y = 8 5 x + 4 .
Решение
Необходимо обратить внимание на область определения. По условию имеем, что функция определена на множестве всех действительных чисел. Раскрываем модуль и решаем систему с промежутками x ∈ — ∞ ; 2 и [ — 2 ; + ∞ ) . Получаем, что
y = — 1 15 x 3 + 18 x 2 + 105 x + 176 , x ∈ — ∞ ; — 2 1 15 x 3 — 6 x 2 + 9 x + 12 , x ∈ [ — 2 ; + ∞ )
Необходимо продифференцировать функцию. Имеем, что
y ‘ = — 1 15 x 3 + 18 x 2 + 105 x + 176 ‘ , x ∈ — ∞ ; — 2 1 15 x 3 — 6 x 2 + 9 x + 12 ‘ , x ∈ [ — 2 ; + ∞ ) ⇔ y ‘ = — 1 5 ( x 2 + 12 x + 35 ) , x ∈ — ∞ ; — 2 1 5 x 2 — 4 x + 3 , x ∈ [ — 2 ; + ∞ )
Когда х = — 2 , тогда производная не существует, потому что односторонние пределы не равны в этой точке:
lim x → — 2 — 0 y ‘ ( x ) = lim x → — 2 — 0 — 1 5 ( x 2 + 12 x + 35 = — 1 5 ( — 2 ) 2 + 12 ( — 2 ) + 35 = — 3 lim x → — 2 + 0 y ‘ ( x ) = lim x → — 2 + 0 1 5 ( x 2 — 4 x + 3 ) = 1 5 — 2 2 — 4 — 2 + 3 = 3
Вычисляем значение функции в точке х = — 2 , где получаем, что
- y ( — 2 ) = 1 15 — 2 + 2 3 — 4 5 ( — 2 ) 2 — 16 5 ( — 2 ) — 26 5 + 3 — 2 + 2 = — 2 , то есть касательная в точке ( — 2 ; — 2 ) не будет существовать.
- Касательная параллельна о х , когда угловой коэффициент равняется нулю. Тогда k x = t g α x = f ‘ ( x 0 ) . То есть необходимо найти значения таких х , когда производная функции обращает ее в ноль. То есть значения f ’ ( x ) и будут являться точками касания, где касательная является параллельной о х .
Когда x ∈ — ∞ ; — 2 , тогда — 1 5 ( x 2 + 12 x + 35 ) = 0 , а при x ∈ ( — 2 ; + ∞ ) получаем 1 5 ( x 2 — 4 x + 3 ) = 0 .
— 1 5 ( x 2 + 12 x + 35 ) = 0 D = 12 2 — 4 · 35 = 144 — 140 = 4 x 1 = — 12 + 4 2 = — 5 ∈ — ∞ ; — 2 x 2 = — 12 — 4 2 = — 7 ∈ — ∞ ; — 2 1 5 ( x 2 — 4 x + 3 ) = 0 D = 4 2 — 4 · 3 = 4 x 3 = 4 — 4 2 = 1 ∈ — 2 ; + ∞ x 4 = 4 + 4 2 = 3 ∈ — 2 ; + ∞
Вычисляем соответствующие значения функции
y 1 = y — 5 = 1 15 — 5 + 2 3 — 4 5 — 5 2 — 16 5 — 5 — 26 5 + 3 — 5 + 2 = 8 5 y 2 = y ( — 7 ) = 1 15 — 7 + 2 3 — 4 5 ( — 7 ) 2 — 16 5 — 7 — 26 5 + 3 — 7 + 2 = 4 3 y 3 = y ( 1 ) = 1 15 1 + 2 3 — 4 5 · 1 2 — 16 5 · 1 — 26 5 + 3 1 + 2 = 8 5 y 4 = y ( 3 ) = 1 15 3 + 2 3 — 4 5 · 3 2 — 16 5 · 3 — 26 5 + 3 3 + 2 = 4 3
Отсюда — 5 ; 8 5 , — 4 ; 4 3 , 1 ; 8 5 , 3 ; 4 3 считаются искомыми точками графика функции.
Рассмотрим графическое изображение решения.
Черная линия – график функции, красные точки – точки касания.
- Когда прямые располагаются параллельно, то угловые коэффициенты равны. Тогда необходимо заняться поиском точек графика функции, где угловой коэффициент будет равняться значению 8 5 . Для этого нужно решить уравнение вида y ‘ ( x ) = 8 5 . Тогда, если x ∈ — ∞ ; — 2 , получаем, что — 1 5 ( x 2 + 12 x + 35 ) = 8 5 , а если x ∈ ( — 2 ; + ∞ ) , тогда 1 5 ( x 2 — 4 x + 3 ) = 8 5 .
Первое уравнение не имеет корней, так как дискриминант меньше нуля. Запишем, что
— 1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 D = 12 2 — 4 · 43 = — 28 0
Другое уравнение имеет два действительных корня, тогда
1 5 ( x 2 — 4 x + 3 ) = 8 5 x 2 — 4 x — 5 = 0 D = 4 2 — 4 · ( — 5 ) = 36 x 1 = 4 — 36 2 = — 1 ∈ — 2 ; + ∞ x 2 = 4 + 36 2 = 5 ∈ — 2 ; + ∞
Перейдем к нахождению значений функции. Получаем, что
y 1 = y ( — 1 ) = 1 15 — 1 + 2 3 — 4 5 ( — 1 ) 2 — 16 5 ( — 1 ) — 26 5 + 3 — 1 + 2 = 4 15 y 2 = y ( 5 ) = 1 15 5 + 2 3 — 4 5 · 5 2 — 16 5 · 5 — 26 5 + 3 5 + 2 = 8 3
Точки со значениями — 1 ; 4 15 , 5 ; 8 3 являются точками, в которых касательные параллельны прямой y = 8 5 x + 4 .
Ответ: черная линия – график функции, красная линия – график y = 8 5 x + 4 , синяя линия – касательные в точках — 1 ; 4 15 , 5 ; 8 3 .
Возможно существование бесконечного количества касательных для заданных функций.
Написать уравнения всех имеющихся касательных функции y = 3 cos 3 2 x — π 4 — 1 3 , которые располагаются перпендикулярно прямой y = — 2 x + 1 2 .
Решение
Для составления уравнения касательной необходимо найти коэффициент и координаты точки касания, исходя из условия перпендикулярности прямых. Определение звучит так: произведение угловых коэффициентов, которые перпендикулярны прямым, равняется — 1 , то есть записывается как k x · k ⊥ = — 1 . Из условия имеем, что угловой коэффициент располагается перпендикулярно прямой и равняется k ⊥ = — 2 , тогда k x = — 1 k ⊥ = — 1 — 2 = 1 2 .
Теперь необходимо найти координаты точек касания. Нужно найти х , после чего его значение для заданной функции. Отметим, что из геометрического смысла производной в точке
x 0 получаем, что k x = y ‘ ( x 0 ) . Из данного равенства найдем значения х для точек касания.
y ‘ ( x 0 ) = 3 cos 3 2 x 0 — π 4 — 1 3 ‘ = 3 · — sin 3 2 x 0 — π 4 · 3 2 x 0 — π 4 ‘ = = — 3 · sin 3 2 x 0 — π 4 · 3 2 = — 9 2 · sin 3 2 x 0 — π 4 ⇒ k x = y ‘ ( x 0 ) ⇔ — 9 2 · sin 3 2 x 0 — π 4 = 1 2 ⇒ sin 3 2 x 0 — π 4 = — 1 9
Это тригонометрическое уравнение будет использовано для вычисления ординат точек касания.
3 2 x 0 — π 4 = a r c sin — 1 9 + 2 πk или 3 2 x 0 — π 4 = π — a r c sin — 1 9 + 2 πk
3 2 x 0 — π 4 = — a r c sin 1 9 + 2 πk или 3 2 x 0 — π 4 = π + a r c sin 1 9 + 2 πk
x 0 = 2 3 π 4 — a r c sin 1 9 + 2 πk или x 0 = 2 3 5 π 4 + a r c sin 1 9 + 2 πk , k ∈ Z
Z — множество целых чисел.
Найдены х точек касания. Теперь необходимо перейти к поиску значений у :
y 0 = 3 cos 3 2 x 0 — π 4 — 1 3
y 0 = 3 · 1 — sin 2 3 2 x 0 — π 4 — 1 3 или y 0 = 3 · — 1 — sin 2 3 2 x 0 — π 4 — 1 3
y 0 = 3 · 1 — — 1 9 2 — 1 3 или y 0 = 3 · — 1 — — 1 9 2 — 1 3
y 0 = 4 5 — 1 3 или y 0 = — 4 5 + 1 3
Отсюда получаем, что 2 3 π 4 — a r c sin 1 9 + 2 πk ; 4 5 — 1 3 , 2 3 5 π 4 + a r c sin 1 9 + 2 πk ; — 4 5 + 1 3 являются точками касания.
Ответ: необходимы уравнения запишутся как
y = 1 2 x — 2 3 π 4 — a r c sin 1 9 + 2 πk + 4 5 — 1 3 , y = 1 2 x — 2 3 5 π 4 + a r c sin 1 9 + 2 πk — 4 5 + 1 3 , k ∈ Z
Для наглядного изображения рассмотрим функцию и касательную на координатной прямой.
Рисунок показывает, что расположение функции идет на промежутке [ — 10 ; 10 ] , где черная прямя – график функции, синие линии – касательные, которые располагаются перпендикулярно заданной прямой вида y = — 2 x + 1 2 . Красные точки – это точки касания.
Видео:Производная функции. 10 класс.Скачать

Касательная к окружности, эллипсу, гиперболе, параболе
Канонические уравнения кривых 2 порядка не являются однозначными функциями. Уравнения касательных для них составляются по известным схемам.
Касательная к окружности
Для задания окружности с центром в точке x c e n t e r ; y c e n t e r и радиусом R применяется формула x — x c e n t e r 2 + y — y c e n t e r 2 = R 2 .
Данное равенство может быть записано как объединение двух функций:
y = R 2 — x — x c e n t e r 2 + y c e n t e r y = — R 2 — x — x c e n t e r 2 + y c e n t e r
Первая функция располагается вверху, а вторая внизу, как показано на рисунке.
Для составления уравнения окружности в точке x 0 ; y 0 , которая располагается в верхней или нижней полуокружности, следует найти уравнение графика функции вида y = R 2 — x — x c e n t e r 2 + y c e n t e r или y = — R 2 — x — x c e n t e r 2 + y c e n t e r в указанной точке.
Когда в точках x c e n t e r ; y c e n t e r + R и x c e n t e r ; y c e n t e r — R касательные могут быть заданы уравнениями y = y c e n t e r + R и y = y c e n t e r — R , а в точках x c e n t e r + R ; y c e n t e r и
x c e n t e r — R ; y c e n t e r будут являться параллельными о у , тогда получим уравнения вида x = x c e n t e r + R и x = x c e n t e r — R .
Касательная к эллипсу
Когда эллипс имеет центр в точке x c e n t e r ; y c e n t e r с полуосями a и b , тогда он может быть задан при помощи уравнения x — x c e n t e r 2 a 2 + y — y c e n t e r 2 b 2 = 1 .
Эллипс и окружность могут быть обозначаться при помощи объединения двух функций, а именно: верхнего и нижнего полуэллипса. Тогда получаем, что
y = b a · a 2 — ( x — x c e n t e r ) 2 + y c e n t e r y = — b a · a 2 — ( x — x c e n t e r ) 2 + y c e n t e r
Если касательные располагаются на вершинах эллипса, тогда они параллельны о х или о у . Ниже для наглядности рассмотрим рисунок.
Написать уравнение касательной к эллипсу x — 3 2 4 + y — 5 2 25 = 1 в точках со значениями x равного х = 2 .
Решение
Необходимо найти точки касания, которые соответствуют значению х = 2 . Производим подстановку в имеющееся уравнение эллипса и получаем, что
x — 3 2 4 x = 2 + y — 5 2 25 = 1 1 4 + y — 5 2 25 = 1 ⇒ y — 5 2 = 3 4 · 25 ⇒ y = ± 5 3 2 + 5
Тогда 2 ; 5 3 2 + 5 и 2 ; — 5 3 2 + 5 являются точками касания, которые принадлежат верхнему и нижнему полуэллипсу.
Перейдем к нахождению и разрешению уравнения эллипса относительно y . Получим, что
x — 3 2 4 + y — 5 2 25 = 1 y — 5 2 25 = 1 — x — 3 2 4 ( y — 5 ) 2 = 25 · 1 — x — 3 2 4 y — 5 = ± 5 · 1 — x — 3 2 4 y = 5 ± 5 2 4 — x — 3 2
Очевидно, что верхний полуэллипс задается с помощью функции вида y = 5 + 5 2 4 — x — 3 2 , а нижний y = 5 — 5 2 4 — x — 3 2 .
Применим стандартный алгоритм для того, чтобы составить уравнение касательной к графику функции в точке. Запишем, что уравнение для первой касательной в точке 2 ; 5 3 2 + 5 будет иметь вид
y ‘ = 5 + 5 2 4 — x — 3 2 ‘ = 5 2 · 1 2 4 — ( x — 3 ) 2 · 4 — ( x — 3 ) 2 ‘ = = — 5 2 · x — 3 4 — ( x — 3 ) 2 ⇒ y ‘ ( x 0 ) = y ‘ ( 2 ) = — 5 2 · 2 — 3 4 — ( 2 — 3 ) 2 = 5 2 3 ⇒ y = y ‘ ( x 0 ) · x — x 0 + y 0 ⇔ y = 5 2 3 ( x — 2 ) + 5 3 2 + 5
Получаем, что уравнение второй касательной со значением в точке
2 ; — 5 3 2 + 5 принимает вид
y ‘ = 5 — 5 2 4 — ( x — 3 ) 2 ‘ = — 5 2 · 1 2 4 — ( x — 3 ) 2 · 4 — ( x — 3 ) 2 ‘ = = 5 2 · x — 3 4 — ( x — 3 ) 2 ⇒ y ‘ ( x 0 ) = y ‘ ( 2 ) = 5 2 · 2 — 3 4 — ( 2 — 3 ) 2 = — 5 2 3 ⇒ y = y ‘ ( x 0 ) · x — x 0 + y 0 ⇔ y = — 5 2 3 ( x — 2 ) — 5 3 2 + 5
Графически касательные обозначаются так:
Касательная к гиперболе
Когда гипербола имеет центр в точке x c e n t e r ; y c e n t e r и вершины x c e n t e r + α ; y c e n t e r и x c e n t e r — α ; y c e n t e r , имеет место задание неравенства x — x c e n t e r 2 α 2 — y — y c e n t e r 2 b 2 = 1 , если с вершинами x c e n t e r ; y c e n t e r + b и x c e n t e r ; y c e n t e r — b , тогда задается при помощи неравенства x — x c e n t e r 2 α 2 — y — y c e n t e r 2 b 2 = — 1 .
Гипербола может быть представлена в виде двух объединенных функций вида
y = b a · ( x — x c e n t e r ) 2 — a 2 + y c e n t e r y = — b a · ( x — x c e n t e r ) 2 — a 2 + y c e n t e r или y = b a · ( x — x c e n t e r ) 2 + a 2 + y c e n t e r y = — b a · ( x — x c e n t e r ) 2 + a 2 + y c e n t e r
В первом случае имеем, что касательные параллельны о у , а во втором параллельны о х .
Отсюда следует, что для того, чтобы найти уравнение касательной к гиперболе, необходимо выяснить, какой функции принадлежит точка касания. Чтобы определить это, необходимо произвести подстановку в уравнения и проверить их на тождественность.
Составить уравнение касательной к гиперболе x — 3 2 4 — y + 3 2 9 = 1 в точке 7 ; — 3 3 — 3 .
Решение
Необходимо преобразовать запись решения нахождения гиперболы при помощи 2 функций. Получим, что
x — 3 2 4 — y + 3 2 9 = 1 ⇒ y + 3 2 9 = x — 3 2 4 — 1 ⇒ y + 3 2 = 9 · x — 3 2 4 — 1 ⇒ y + 3 = 3 2 · x — 3 2 — 4 и л и y + 3 = — 3 2 · x — 3 2 — 4 ⇒ y = 3 2 · x — 3 2 — 4 — 3 y = — 3 2 · x — 3 2 — 4 — 3
Необходимо выявить, к какой функции принадлежит заданная точка с координатами 7 ; — 3 3 — 3 .
Очевидно, что для проверки первой функции необходимо y ( 7 ) = 3 2 · ( 7 — 3 ) 2 — 4 — 3 = 3 3 — 3 ≠ — 3 3 — 3 , тогда точка графику не принадлежит, так как равенство не выполняется.
Для второй функции имеем, что y ( 7 ) = — 3 2 · ( 7 — 3 ) 2 — 4 — 3 = — 3 3 — 3 ≠ — 3 3 — 3 , значит, точка принадлежит заданному графику. Отсюда следует найти угловой коэффициент.
y ‘ = — 3 2 · ( x — 3 ) 2 — 4 — 3 ‘ = — 3 2 · x — 3 ( x — 3 ) 2 — 4 ⇒ k x = y ‘ ( x 0 ) = — 3 2 · x 0 — 3 x 0 — 3 2 — 4 x 0 = 7 = — 3 2 · 7 — 3 7 — 3 2 — 4 = — 3
Ответ: уравнение касательной можно представить как
y = — 3 · x — 7 — 3 3 — 3 = — 3 · x + 4 3 — 3
Наглядно изображается так:
Касательная к параболе
Чтобы составить уравнение касательной к параболе y = a x 2 + b x + c в точке x 0 , y ( x 0 ) , необходимо использовать стандартный алгоритм, тогда уравнение примет вид y = y ‘ ( x 0 ) · x — x 0 + y ( x 0 ) . Такая касательная в вершине параллельна о х .
Следует задать параболу x = a y 2 + b y + c как объединение двух функций. Поэтому нужно разрешить уравнение относительно у . Получаем, что
x = a y 2 + b y + c ⇔ a y 2 + b y + c — x = 0 D = b 2 — 4 a ( c — x ) y = — b + b 2 — 4 a ( c — x ) 2 a y = — b — b 2 — 4 a ( c — x ) 2 a
Графически изобразим как:
Для выяснения принадлежности точки x 0 , y ( x 0 ) функции, нежно действовать по стандартному алгоритму. Такая касательная будет параллельна о у относительно параболы.
Написать уравнение касательной к графику x — 2 y 2 — 5 y + 3 , когда имеем угол наклона касательной 150 ° .
Решение
Начинаем решение с представления параболы в качестве двух функций. Получим, что
— 2 y 2 — 5 y + 3 — x = 0 D = ( — 5 ) 2 — 4 · ( — 2 ) · ( 3 — x ) = 49 — 8 x y = 5 + 49 — 8 x — 4 y = 5 — 49 — 8 x — 4
Значение углового коэффициента равняется значению производной в точке x 0 этой функции и равняется тангенсу угла наклона.
k x = y ‘ ( x 0 ) = t g α x = t g 150 ° = — 1 3
Отсюда определим значение х для точек касания.
Первая функция запишется как
y ‘ = 5 + 49 — 8 x — 4 ‘ = 1 49 — 8 x ⇒ y ‘ ( x 0 ) = 1 49 — 8 x 0 = — 1 3 ⇔ 49 — 8 x 0 = — 3
Очевидно, что действительных корней нет, так как получили отрицательное значение. Делаем вывод, что касательной с углом 150 ° для такой функции не существует.
Вторая функция запишется как
y ‘ = 5 — 49 — 8 x — 4 ‘ = — 1 49 — 8 x ⇒ y ‘ ( x 0 ) = — 1 49 — 8 x 0 = — 1 3 ⇔ 49 — 8 x 0 = — 3 x 0 = 23 4 ⇒ y ( x 0 ) = 5 — 49 — 8 · 23 4 — 4 = — 5 + 3 4
Имеем, что точки касания — 23 4 ; — 5 + 3 4 .
Ответ: уравнение касательной принимает вид
📸 Видео
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ МОДУЛЯСкачать

Уравнение с модулем через геометрический смысл #егэ2024Скачать

Геометрический смысл производной / самое простое объяснениеСкачать





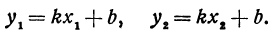
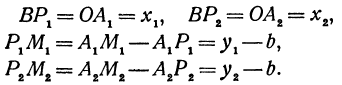
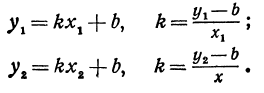
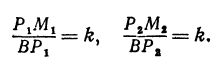




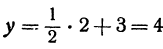
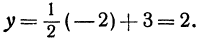
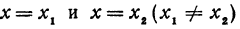
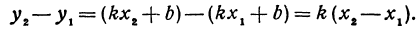
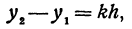
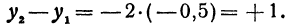
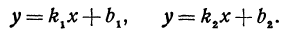
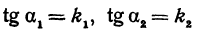
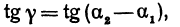
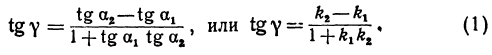
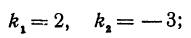
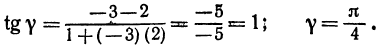
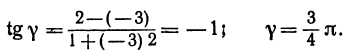
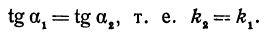
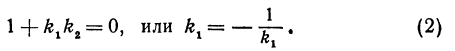
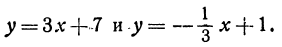

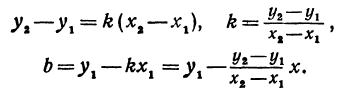
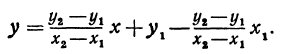
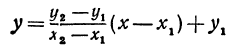

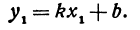
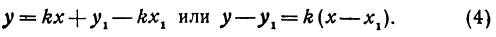
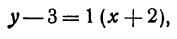
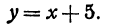


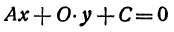
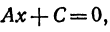
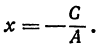
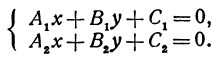
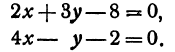
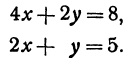
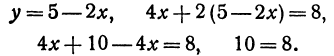
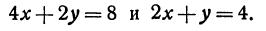
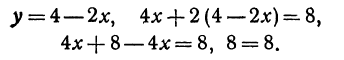
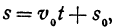
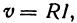
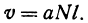
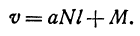
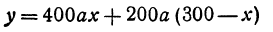
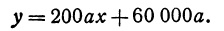


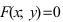
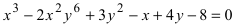
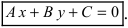
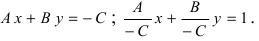
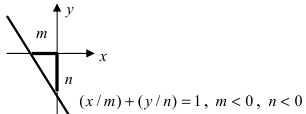
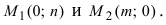
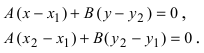
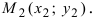
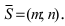
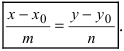
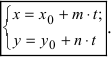
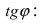
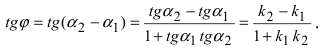
 параллельны или совпадают
параллельны или совпадают то
то 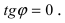 Отсюда следует условие параллельности прямых: угловые коэффициенты прямых равны между собой
Отсюда следует условие параллельности прямых: угловые коэффициенты прямых равны между собой 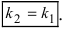
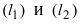 перпендикулярны
перпендикулярны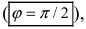 то
то 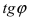 не существует.
не существует.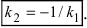
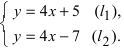
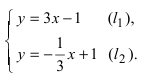
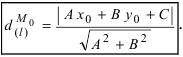
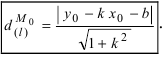
 0, у>0;
0, у>0; 0, у
0, у 0;
0; 0.
0.