п.1. Количество корней кубического уравнения
Кубическое уравнение $$ ax^3+bx^2+cx+d=0 $$ на множестве действительных чисел может иметь один, два или три корня.
С помощью производной можно быстро ответить на вопрос, сколько корней имеет данное уравнение. begin f(x)=ax^3+bx^2+cx+d\ f'(x)=3ax^2+bx+c end Если в уравнении (f'(x)=0) дискриминант (D=4b^2-12ac=4(b^2-3ac)gt 0), кубическая парабола имеет две точки экстремума: (x_=frac<-2bpmsqrt>). Если при этом значения функции в точках экстремума (f(x_1)cdot f(x_2)lt 0), т.е. расположены по разные стороны от оси OX, парабола имеет три точки пересечения с этой осью. Исходное уравнение имеет три корня.
Если две точки экстремума найдены, но (f(x_1)cdot f(x_2)=0), уравнение имеет два корня.
Во всех остальных случаях – у исходного уравнения 1 корень.
Пример 1. Сколько корней имеют уравнения:
| 1) (x^3+3x^2-4=0) (b^2-3ac=9gt 0 (c=0) ) (f(x)=x^3+3x^2-4 ) (f'(x)=3x^2+6x=3x(x+2) ) (x_1=0, x_2=-2 ) (f(x_1)=-4, f(x_2)=0 ) (f(x_1)cdot f(x_2)=0Rightarrow) два корня  | 2) (x^3+3x^2-1=0) (b^2-3ac=9gt 0 ) (f(x)=x^3+3x^2-1 ) (f'(x)=3x^2+6x=3x(x+2) ) (x_1=0, x_2=-2 ) (f(x_1)=-1, f(x_2)=3 ) (f(x_1)cdot f(x_2)lt 0Rightarrow) три корня  |
| 3) (x^3+3x^2+1=0) (b^2-3ac=9gt 0) (f(x)=x^3+3x^2+1 ) (f'(x)=3x^2+6x=3x(x+2) ) (x_1=0, x_2=-2 ) (f(x_1)=1, f(x_2)=5 ) (f(x_1)cdot f(x_2)gt 0Rightarrow) один корень  | 4) (x^3+x^2+x+3=0) (b^2-3ac=1-3lt 0 ) Один корень  |
п.2. Количество корней произвольного уравнения
Задачи на подсчет количества корней решаются с помощью построения графиков при полном или частичном исследовании функций.
Пример 2. а) Найдите число корней уравнения (frac 1x+frac+frac)
б) Найдите число корней уравнения (frac 1x+frac+frac=k)
Построим график функции слева, а затем найдем для него количество точек пересечения с горизонталью (y=1). Это и будет ответом на вопрос задачи (а).
Исследуем функцию: $$ f(x)=frac1x+frac+frac $$ Алгоритм исследования и построения графика – см. §49 данного справочника.
1) ОДЗ: (xneleft)
Все три точки – точки разрыва 2-го рода. begin lim_left(frac1x+frac+fracright)=-infty-1-frac13=-infty\ lim_left(frac1x+frac+fracright)=+infty-1-frac13=+infty\ lim_left(frac1x+frac+fracright)=1-infty-frac12=-infty\ lim_left(frac1x+frac+fracright)=1+infty-frac12=+infty\ lim_left(frac1x+frac+fracright)=frac13+frac12-infty=-infty\ lim_left(frac1x+frac+fracright)=frac13+frac12+infty=+infty end 2) Функция ни четная, ни нечетная.
Функция непериодическая.
3) Асимптоты
1. Вертикальные (x=0, x=1, x=3) – точки разрыва 2-го рода
2. Горизонтальные: begin lim_left(frac1x+frac+fracright)=-0-0-0=-0\ lim_left(frac1x+frac+fracright)=+0+0+0=+0\ end Горизонтальная асимптота (y=0)
На минус бесконечности функция стремится к 0 снизу, на плюс бесконечности – сверху.
3. Наклонные: (k=0), нет.
4) Первая производная $$ f'(x)=-frac-frac-fraclt 0 $$ Производная отрицательная на всей ОДЗ.
Функция убывает.
5) Вторую производную не исследуем, т.к. перегибы не влияют на количество точек пересечения с горизонталью.
6) Точки пересечения с OY – нет, т.к. (x=0) – асимптота
Точки пересечения с OX – две, (0lt x_1lt 1,1lt x_2lt 3)
7) График
Получаем ответ для задачи (а) 3 корня.
Решаем более общую задачу (б). Передвигаем горизонталь (y=k) снизу вверх и считаем количество точек пересечения с графиком функции. Последовательно, получаем:
При (klt 0) — три корня
При (k=0) — два корня
При (kgt 0) — три корня
Ответ: а) 3 корня; б) при (k=0) два корня, при (kne 0) три корня.
Пример 3. Найдите все значения параметра a, при каждом из которых уравнение $$ sqrt+sqrt=a $$ имеет по крайней мере одно решение.
Исследуем функцию (f(x)=sqrt+sqrt)
ОДЗ: ( begin x-1geq 0\ 10-2xgeq 0 end Rightarrow begin xgeq 1\ xleq 5 end Rightarrow 1leq xleq 5 )
Функция определена на конечном интервале.
Поэтому используем сокращенный алгоритм для построения графика.
Значения функции на концах интервала: (f(1)=0+sqrt=2sqrt, f(5)=sqrt+0=2)
Первая производная: begin f'(x)=frac<2sqrt>+frac<2sqrt>=frac<2sqrt>-frac<sqrt>\ f'(x)=0 text 2sqrt=sqrtRightarrow 4(x-1)=10-2xRightarrow 6x=14Rightarrow x=frac73\ fleft(frac73right)=sqrt+sqrt=sqrt+sqrt<frac>=frac<sqrt>=2sqrt end Промежутки монотонности:
| (x) | 1 | (1; 7/3) | 7/3 | (7/3; 5) | 5 |
| (f'(x)) | ∅ | + | 0 | — | ∅ |
| (f(x)) | (2sqrt) | (nearrow ) | max (2sqrt) | (searrow ) | 2 |
Можем строить график:
(y=a) — горизонтальная прямая.
Количество точек пересечения (f(x)) и (y) равно количеству решений.
Получаем:
| $$ alt 2 $$ | нет решений |
| $$ 2leq alt 2sqrt $$ | 1 решение |
| $$ 2sqrtleq alt 2sqrt $$ | 2 решения |
| $$ a=2sqrt $$ | 1 решение |
| $$ agt 2sqrt $$ | нет решений |
По крайней мере одно решение будет в интервале (2leq aleq 2sqrt).
п.3. Решение неравенств с построением графиков
Пример 4. Решите неравенство (fracgt frac)
Разобьем неравенство на совокупность двух систем.
Если (xgt 1), то (x-1gt 0), на него можно умножить слева и справа и не менять знак.
Если (xlt 1), то (x-1lt 0), умножить также можно, только знак нужно поменять.
Сразу учтем требование ОДЗ для логарифма: (xgt 0)
Получаем совокупность: begin left[ begin begin xgt 1\ 2+log_3 xgtfrac end \ begin 0lt xlt 1\ 2+log_3 xltfrac end end right. \ 2+log_3 xgt fracRightarrow log_3 xgt fracRightarrow log_3 xgt frac\ left[ begin begin xgt 1\ log_3 xgtfrac end \ begin 0lt xlt 1\ log_3 xltfrac end end right. end Исследуем функцию (f(x)=frac=frac=1-frac)
Точка разрыва: (x=frac12) – вертикальная асимптота
Односторонние пределы: begin lim_left(1-fracright)=1-frac=+infty\ lim_left(1-fracright)=1-frac=-infty end Второе слагаемое стремится к 0 на бесконечности, и это дает горизонтальную асимптоту: (y=1) begin lim_left(1-fracright)=1-frac=1+0\ lim_left(1-fracright)=1-frac=1-0 end На минус бесконечности кривая стремится к (y=1) сверху, а на плюс бесконечности – снизу.
Первая производная: $$ f'(x)=left(1-fracright)’=fracgt 0 $$ Производная положительная на всей ОДЗ, функция возрастает.
Вторая производная: $$ f»(x)=-frac $$ Одна критическая точка 2-го порядка (x=frac12)
Видео:Отбор корней по окружностиСкачать

Как найти k и b по графику линейной функции?
В новой 9 задаче профильного ЕГЭ много заданий на линейные функции. Самое сложное, что нужно сделать, решая эти задачи – определить формулу линейной функции , т.е. найти (k) и (b) по графику. Примеры таких заданий (решения будут внизу статьи):
В статье я расскажу про два простых способа найти (k) и (b), если известен график линейной функции.
Видео:3,5 способа отбора корней в тригонометрии | ЕГЭ по математике | Эйджей из ВебиумаСкачать

Способ 1
Первый способ основывается на трех фактах:
Линейная функция пересекает ось (y) в точке (b).
Примеры:
Но не советую определять так (b), если прямая пересекает ось не в целом значении или если точка пересечения вообще не видна на графике. Для таких случаев пользуйтесь вторым способом.
Если функция возрастает, то знак коэффициента (k) плюс, если убывает – минус, а если постоянна, то (k=0).
Чтоб конкретнее определить (k) надо построить на прямой прямоугольный треугольник так, чтобы гипотенуза лежала на графике функции, а вершины треугольника совпадали с вершинами клеточек. Далее, чтоб определить (k) нужно вертикальную сторону треугольника поделить на горизонтальную и поставить знак согласно возрастанию/убыванию функции.

Давайте пока что не будем искать формулу иррациональной функции, сосредоточимся только на линейной функции.
(b=3) – это сразу видно. Функция идет вниз, значит (k 0). (k=+frac=frac=1,b=1). (f(x)=x+1).
Теперь перейдем к функции (g(x)). Найдем координаты точек (D) и (E): (D(-2;4)), (E(-4;1)). Можно составить систему:
Вычтем второе уравнение из первого, чтоб убрать (b):
(g(x)=1,5x+7). Обе функции найдены, теперь можно найти абсциссу (икс) точки пересечения. Приравняем (f(x)) и (g(x)).
Картинку в хорошем качестве, можно скачать нажав на кнопку «скачать статью».
Видео:Определить число корней уравнения. Determine the number of roots of the equation.Скачать

Квадратичная функция и ее график
В этой статье мы поговорим о том, что такое квадратичная функция, научимся строить ее график и определять вид графика в зависимости от знака дискриминанта и знака старшего коэффициента.
Итак.
Функция вида 


В уравнении квадратичной функции:
a — старший коэффициент
b — второй коэффициент
с — свободный член.
Графиком квадратичной функции является квадратичная парабола, которая для функции 
Обратите внимание на точки, обозначенные зелеными кружками — это, так называемые «базовые точки». Чтобы найти координаты этих точек для функции 
Внимание! Если в уравнении квадратичной функции старший коэффициент 

График функции 
Для нахождения координат базовых точек составим таблицу:
Обратите внимание, что график функции 

Итак, мы заметили:
Если старший коэффициент a>0 , то ветви параболы напрaвлены вверх .
Если старший коэффициент a , то ветви параболы напрaвлены вниз .
Второй параметр для построения графика функции — значения х, в которых функция равна нулю, или нули функции. На графике нули функции 

Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю, чтобы найти координаты точек пересечения графика функции 

В случае квадратичной функции 

В процессе решения квадратного уравнения мы находим дискриминант: 
И здесь возможны три случая:
1. Если 




2. Если 




3 . Если 




Если 

Следовательно, зная направление ветвей параболы и знак дискриминанта, мы уже можем в общих чертах определить, как выглядит график нашей функции.
Следующий важный параметр графика квадратичной функции — координаты вершины параболы:
Прямая, проходящая через вершину параболы параллельно оси OY является осью симметрии параболы.
И еще один параметр, полезный при построении графика функции — точка пересечения параболы 
Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы 

То есть точка пересечения параболы с осью OY имеет координаты (0;c).
Итак, основные параметры графика квадратичной функции показаны на рисунке:
Рассмотрим несколько способов построения квадратичной параболы. В зависимости от того, каким образом задана квадратичная функция, можно выбрать наиболее удобный.
1. Функция задана формулой 
Рассмотрим общий алгоритм построения графика квадратичной параболы на примере построения графика функции
1. Направление ветвей параболы.
Так как 

2. Найдем дискриминант квадратного трехчлена

Дискриминант квадратного трехчлена больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ.
Для того, чтобы найти их координаты, решим уравнение:

3. Координаты вершины параболы:
4. Точка пересечения параболы с осью OY: (0;-5),и ей симметричная относительно оси симметрии параболы.
Нанесем эти точки на координатную плоскость, и соединим их плавной кривой:
Этот способ можно несколько упростить.
1. Найдем координаты вершины параболы.
2. Найдем координаты точек, стоящих справа и слева от вершины.
Воспользуемся результатами построения графика функции
Кррдинаты вершины параболы
Ближайшие к вершине точки, расположенные слева от вершины имеют абсциссы соответственно -1;-2;-3
Ближайшие к вершине точки, расположенные справа имеют абсциссы соответственно 0;1;2
Подставим значения х в уравнение функции, найдем ординаты этих точек и занесем их в таблицу:
Нанесем эти точки на координатную плоскость и соединим плавной линией:
2 . Уравнение квадратичной функции имеет вид 

или в уравнении квадратичной функции 
Построим для примера график функции 
Вспомним линейные преобразования графиков функций. Чтобы построить график функции 
- сначала построить график функции
,
- затем одинаты всех точек графика умножить на 2,
- затем сдвинуть его вдоль оси ОХ на 1 единицу вправо,
- а затем вдоль оси OY на 4 единицы вверх:
Теперь рассмотрим построение графика функции 

Выделим в уравнении функции полный квадрат:
Следовательно, координаты вершины параболы: 
3 . Уравнение квадратичной функции имеет вид y=(x+a)(x+b)
Построим для примера график функции y=(x-2)(x+1)
1. Вид уравнения функции позволяет легко найти нули функции — точки пересечения графика функции с осью ОХ:
(х-2)(х+1)=0, отсюда
2. Координаты вершины параболы:
3. Точка пересечения с осью OY: с=ab=(-2)(1)=-2 и ей симметричная.
Нанесем эти точки на координатную плоскость и построим график:
График квадратичной функции.
Перед вами график квадратичной функции вида 
Кликните по чертежу.
Подвигайте движки.
Исследуйте зависимость
— ширины графика функции 

— сдвига графика функции 


— сдвига графика функции 
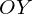

— направления ветвей параболы от знака коэффициента 
— координат вершины параболы 


И.В. Фельдман, репетитор по математике.
📽️ Видео
Отбор корней тригонометрического уравнения с помощью графикаСкачать

Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

7 класс, 35 урок, Графическое решение уравненийСкачать

Число корней уравнения в кольце. Теорема РушеСкачать

Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать

Как найти корни уравнения в Excel с помощью Подбора параметраСкачать

ФУНКЦИЯ y = √¯x ( корень из х ) МАТЕМАТИКАСкачать
Как определить уравнение параболы по графику?Скачать

Формула корней квадратного уравнения. Алгебра, 8 классСкачать

СЛОЖИТЕ ДВА КОРНЯСкачать

Функция "Корень n-й степени из х"Скачать

Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Корень n-ой степени из действительного числа и его свойства. 11 класс.Скачать

10 класс, 43 урок, Уравнение касательной к графику функцииСкачать

Как по графику первообразной определить количество корней уравнения y=fxСкачать

Построить график ЛИНЕЙНОЙ функции и найти:Скачать

АЛГЕБРА 7 класс : Уравнение и его корни | ВидеоурокСкачать











































