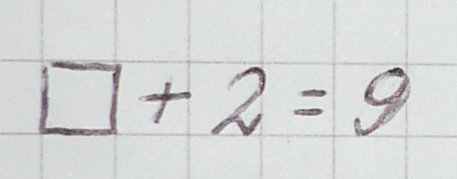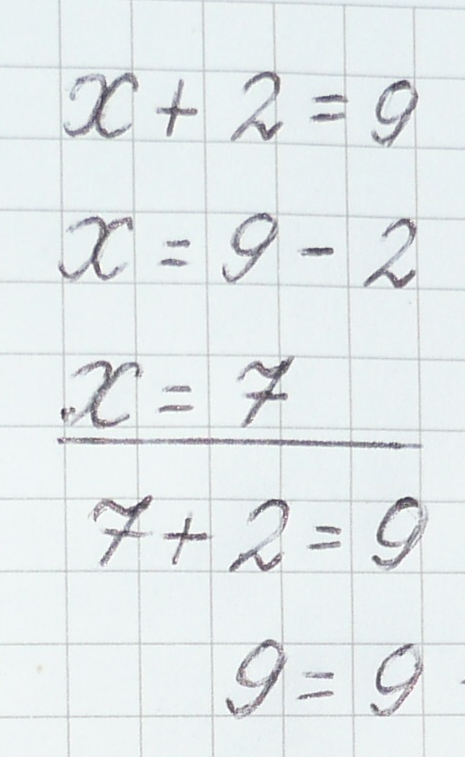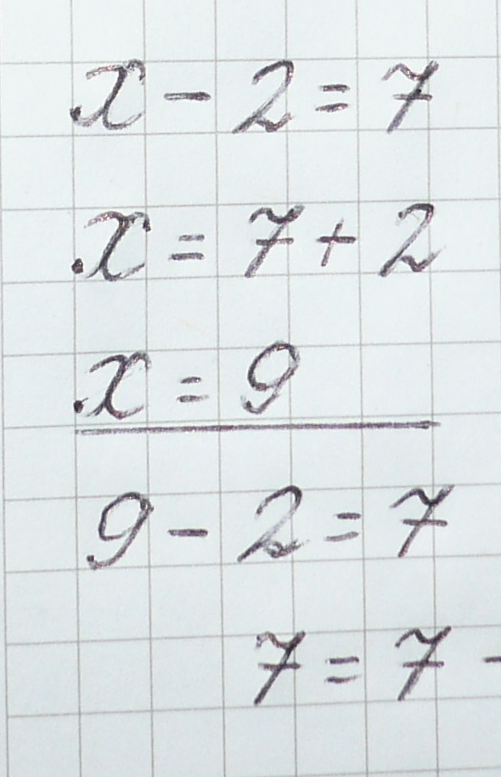Как оформлять уравнение в начальной школе

Порядок оформления записей в тетрадях по математике в начальной школе

Видео:Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

Скачать:

Видео:Как оформлять работу по математике в начальной школеСкачать

Предварительный просмотр:

Образцы оформления заданий на уроках математики

В ходе работы на уроках математики возникают частные вопросы оформления отдельных заданий: решения задач, нахождения значения числовых выражений, уравнений, неравенств, выполнения геометрических заданий.

Рассмотрим примерные рекомендации по оформлению отдельных заданий младшими школьниками в тетрадях по математике.

Во-первых, необходимо научить младших школьников легко определять количество строк, которые следует пропускать.

Между работами — 4 клетки, внутри работы между заданиями — 2 клетки, внутри заданий между действиями — 1 клетку (образец 1).

Требования к написанию цифр как в однозначных числах, так и в многозначных предъявляются единые. Каждая цифра пишется с наклоном в отдельной клетке, прислоняясь к её правой стороне. Особенно это требование актуально при выполнении действий с многозначными числами. Образцы написания цифр представлены в учебном наглядном пособии «Демонстрационный набор письменных цифр и математических знаков».

Во II классе учащимся удобнее все буквы в тетрадях по математике писать высотой в целую клетку (аналогично письму на уроках языка). В III и IV классах высота букв при повышении скорости письма может уменьшаться до 2/3 высоты клетки.

После даты, слов Домашняя работа, Классная работа. Задача точка не ставится. Слова Примеры, Уравнения, Неравенств, Математический диктант, Контрольный устный счёт в начальных классах не пишутся.

Как ученику II класса (именно в этом возрасте они начинают записывать дату выполнения работы) научиться определять место начала записи Даты? Например, можно договориться отсчитывать от начала страницы (или от полей) 10 полных клеток, а в 11-й начинать запись даты, тогда будет достигнуто единство оформления письменных записей и ученику легко будет расположить дату посередине страницы.

Оформление математических диктантов может быть выполнено разными способами. Учащиеся I класса пишут под диктовку числа, учатся писать математические диктанты, записывая результаты в строку через запятую. Начиная со II класса результаты диктанта можно оформлять в строку или в столбики. Учащиеся должны быть научены фиксировать ответы по-разному. Перед математическим диктантом учитель оговаривает с учащимися способ записи ответов. При записи результатов математического диктанта в строку учащиеся пишут каждый последующий результат через запятую. В случае отсутствия ответа

на месте его ученик ставит прочерк. В противном случае проверка результатов выполненного диктанта вызовет затруднения, как у учителя, так и учащихся (при самопроверке и при взаимопроверке). (Образец 2.)

Запись результатов математического диктанта может быть выполнена в столбики. Для этого перед началом диктанта учитель сообщает классу количество заданий предстоящего диктанта (10 или 12). Учащиеся до диктанта записывают половину порядковых номеров ответов (5 или 6) в первый столбик, а вторую половину — во второй, отступив вправо от записанных номеров заданий первого столбика оговоренное количество клеток, например 10. Порядковые номера заданий записываются с круглой скобкой.

В ходе выполнения математического диктанта учащиеся записывают ответ рядом с порядковым номером. Ответы, в которых учащийся сомневается, могут быть им пропущены. Заполнение их возможно и при самопроверке. Перед тем как отдать работу на проверку учителю или однокласснику, ученик должен рядом с номерами невыполненных заданий поставить прочерк. (Образец 3.)

В IV классе при изучении нумерации многозначных чисел фиксация результатов математического диктанта может производиться в один столбик. (Образец 4.)

В оформление задачи входит слово Задача, запись решения и ответа.

Слово Задача записывается с большой буквы посередине строки. Ориентировочно необходимо отступить от левого края страницы 10 клеток. Если запись слова Задача располагается на той же странице, что и дата, то учащимся удобно провести по воздуху линию от первой цифры даты вниз, так как первая буква слова будет расположена под первой цифрой даты. (См. образец 1.)

В I классе решение задачи записывается в виде числового выражения. Значение числового выражения (ответ задачи) подчёркивается. Полный ответ задачи проговаривается устно. (Образец 5.)

Со II класса пишутся слова Задача и Ответ. Второклассники учатся оформлять запись решения составной задачи. При записи решения задачи по действиям каждое действие пишется с новой строки. В начале строки ставится порядковый номер действия с круглой скобкой, отступается одна клетка и записывается действие. (Образец 6.)

Запись решения задачи может быть оформлена выражением. В этом случае порядковый номер в начале строки не ставится. (Образец 7.)

В III и IV классах решение может быть оформлено по действиям без пояснений, с полными или краткими пояснениями, с вопросами, с планом, а также выражением. Если решение задачи записывается выражением, то нет необходимости делать пояснения после действия. Результат поясняется только в ответе.

Решение задачи по действиям с краткими пояснениями

оформляется следующим образом. Пояснения к каждому из действий формулируются кратко (словосочетанием). Сразу после наименования ставится тире, и с маленькой буквы записывается пояснение, в котором заключается основной смысл ответа на поставленный вопрос. (Образец 8.)

Решение задачи по действиям с полными пояснениями оформляется следующим образом. (Образец 9.)

Решение задачи с вопросами предполагает постановку» вопросов к каждому из действий. Вопрос записывается с большой буквы с начала строки. После него ставится вопросительный знак, а затем с новой строки записывается действие. Порядковый номер действия в этом случае ставится один раз перед вопросом. (Образец 10.)

Решение этой же задачи можно оформить с планом. (Образец 11.)

При необходимости выполнить письменные вычисления решение задачи записывается сразу в столбик. (Образец 12.)

Если решение задачи записывается выражением, при этом необходимо произвести письменные вычисления, они располагаются под выражением. (Образец 13.)

Наименование пишется после каждого действия задачи или после выражения в скобках с маленькой буквы. В записи наименования допускаются сокращения (обязательно должно заканчиваться на согласный). После сокращения ставится точка, в случаях, если это сокращение не является общепринятым. Точка не ставится в наименованиях, обозначающих единицы измерения длины: мм, см, дм, м, км, единицы измерения веса: г, кг, т, ц, единицы измерения времени: суг, ч, мин, с.

Слово Ответ записывается с начала строки, после него ставится двоеточие. После двоеточия на первом месте желательно записать число (результат решения задачи), а после него с_ маленькой буквы пояснение к нему. Ответ задачи может записываться как целыми словами, так и с использованием общепринятых сокращений (километров — км, метров — м, километров в час — км/ч и т. п.). Ответ записывается к каждой задаче.

В случае если задача решается несколькими способами, делается пометка «1 способ, 2 способ» и ответ записывается один раз. Если решение задачи записано по действиям, а затем выражением, то ответ тоже записывается один раз. Если решение задачи выполнялось с полным пояснением, с записью вопросов по действиям, ответ может быть записан кратко. При этом записывается числовое значение и наименование либо число и словосочетание, отражающие ответ задачи. (См. образцы 9, 10, 11.) Если решение задачи записано выражением, по действиям с краткими пояснениями или без них, то ответ задачи должен быть полным (в виде числа и предложения). (См. образцы 6, 7, 8, 12, 13.)

К задаче может быть выполнена краткая запись. Она записывается после слова Задача. Между строками пропускается одна клетка. Буквы и цифры пишутся в соответствии с рассмотренными выше требованиями.

Запись нахождения значения математического выражения также оформляется единообразно. Если математическое выражение состоит из одного действия, которое решается устно, ученик записывает его в строку и рядом — его ответ. При записи нескольких таких выражений между столбиками рекомендуется пропускать в сторону 3 клетки, а вниз между столбиками — 2. (Образец 14.)

Если математическое выражение состоит из одного действия, и для его решения требуются письменные вычисления, то оно сразу записывается в столбик и вычисляется. В строке можно разместить несколько математических выражений с письменными вычислениями при условии, что вправо между ними необходимо пропускать не менее 3 клеток. (Образец 15.)

При письменном умножении на трёхзначное число следует рекомендовать учащимся размещать на одной строке только 2 примера, так как при записи происходит значительный сдвиг влево. При необходимости на строке размешается математическое выражение, а рядом проверка вычислений. (Образец 16.)

Учащийся вправе сам принять решение о рациональном размещении на странице выполненных заданий. К примеру, если необходимо выполнить несколько примеров на деление многозначных чисел и сделать к ним проверку, на одной строке можно разместить примеры на деление, а под ними проверку. В таких случаях рекомендуется отступать вниз 2 клетки. (Образец 17.)

Если математическое выражение состоит из нескольких действий, решение которых предполагает устные вычисления, то учащийся сначала определяет порядок действий (его можно надписать над выражением), затем производит устные вычисления и записывает ответ. Выполнять запись устных действий не нужно. (Образец 18.)

Если математическое выражение состоит из нескольких действий, решение которых предполагает письменные вычисления, то сначала оно записывается в строку. Определяется порядок выполнения действий. Затем каждое действие записывается под выражением и выполняется. Полученный конечный результат записывается в первоначальную запись после знака «равно». (Образец 19.)

Решение простейшего уравнения записывается в столбик: само уравнение, способ нахождения неизвестного, результат вычисления (значение неизвестного), проверка решения уравнения. Можно расположить решение двух уравнений в 2 столбика. При этом между уравнениями в сторону необходимо отступить 3 клетки. Слова Решение

и Проверка, которые используются в

образце оформления уравнения на страницах учебника, в тетрадях учащимися не записываются. (Образец 20.)

Решение уравнений в два действия также записывается в столбик. Расположение двух таких уравнений также допустимо на одной строке при условии, что их решение не требует письменных вычислений. (Образец 21.)

Если при решении уравнения необходимо выполнять письменные действия с многозначными числами, их следует располагать справа от записи решения уравнения. (Образец 22.)

Сравнение чисел, выражений, величин. При сравнении двух чисел они записываются на строке с интервалом в одну клетку. В ней учащийся ставит знак. (Образец 23.)

При сравнении многозначных чисел учащийся производит сравнение поразрядно. Достаточно обратить внимание на различающиеся цифры в разрядах, начиная с высшего, подчеркнуть их. Во второй строке можно записать только те цифры, которыми различаются числа. Это будет основанием для сравнения чисел. (Образец 24.)

Если число необходимо сравнить с выражением, то в записи между ними также оставляется клетка. Знак может быть вставлен только после нахождения значения выражения и сопоставления его с числом. (Образец 25.)

Если необходимо сравнить два выражения, то в записи между ними также оставляется клетка. Знак может быть вставлен только после нахождения значений обоих выражений. Найденные значения выражений целесообразно записать на следующей строке и после их сопоставления поставить знак сравнения между ними, а затем и на верхней строке в исходном выражении. (Образец 26.)

При сравнении величин обращается внимание на единицы их измерения. Если величины выражены в одинаковых единицах измерения, то сравнение производится так же, как и сравнение чисел. Знак ставится между величинами после установления их равенства или неравенства. (Образец 27.)

Если сравниваются величины, выраженные в разных единицах измерения, необходимо оценить возможность их сравнения без приведения их к единым единицам измерения; если это возможно, поставить требующийся знак. (Образец 28.)

При сравнении величин, выраженных в разных единицах измерения, чаще всего обязательным условием является приведение их к одинаковым единицам (меньшим или большим). Запись лучше зафиксировать на следующей строке. После сопоставления преобразованных величин можно поставить знак равенства или неравенства и затем перенести его в исходное выражение. (Образец 29.)

Задания геометрического характера могут включать только вычерчивание геометрических фигур, только нахождение параметров геометрических фигур, либо задание на нахождение параметров и вычерчивание фигур.

Если задание предполагает только вычерчивание фигуры (фигур), от предыдущего задания отступают две клетки и чертят заданную геометрическую фигуру.

Если задание предполагает только нахождение параметров геометрической фигуры, то ученик должен оформить выполнение задания как решение задачи: слово Задача, решение (нахождение параметров геометрической фигуры), ответ. Если в задаче не требуется вычерчивание фигуры, этого и не нужно делать. (Образец 30.)

Если задание предполагает нахождение параметров и вычерчивание фигуры, то оформляется это тоже как задача. Ученик должен привыкнуть к тому, что любые вычисления (даже устные) при нахождении параметров должны быть зафиксированы письменно. Сначала проводятся вычисления, затем вычерчивается фигура с полученными данными. (Образец 31.)

В задании может быть задана длина первого отрезка. Второй и третий отрезки необходимо найти, а затем начертить. В таком случае ребёнку удобно начертить данный отрезок, вычислить размер второго отрезка (с записью действия), начертить полученный отрезок, затем найти длину третьего отрезка (с записью действия) и тогда его начертить. (Образец 32.)

Это же задание учащийся может оформить иначе. (Образец 33.)

Если к заданию было записано слово Задача, значит, к нему предполагается и Ответ.

Если необходимо произвести сравнение отрезков, значит, за писывается слово Задача, после вычерчивания отрезков записывается математическое действие, с помощью которого производилось сравнение (вычитание, деление). Завершается выполнение задания записью ответа.

Отметим некоторые особенности вычерчивания отрезков.

• Чертим отрезки, отступая от левого края страницы 1 полную клетку.
• Все отрезки необходимо чертить друг под другом, при этом их начальные точки должны находиться на одном расстоянии от левого края страницы.
• Пропуски между отрезками вниз составляют 1 клетку.
• Края отрезков отмечаются небольшими штрихами.

Нахождение значения выражения с переменной записывается следующим образом. (Образец 34.)

Требования к оформлению контрольных работ. Оформление их производится так же, как и классных работ. Исправления делаются в случае необходимости аккуратно. Краткая запись к задаче, вопросы, пояснения, которые помогают при обучении решению задач, в контрольной работе не требуются, так как их использование часто влечёт множество орфографических ошибок, не отражающих реальные математические знания детей. Формулировки заданий контрольной работы учащимися не переписываются в тетрадь. Ставится лишь порядковый номер выполняемого задания.

Порядок выполнения заданий контрольной работы учащийся может выбрать сам. Записывая решения заданий, он должен ставить тот порядковый номер задания, под которым оно стоит в контрольной работе. (Образец 36.)

Хочется отметить, что далеко не все частные случаи оформления записей по математике удалось осветить в статье. Кроме того, прописанные в данной статье рекомендации являются примерными. Если учителем, методическим объединением учителей наработаны более рациональные приёмы обучения учащихся оформлению записей в тетрадях по математике без нарушения общепринятых норм, они имеют право внедрять их в свою деятельность. Важным остаётся требование единообразия оформления записей всеми учащимися.

Работа по формированию у младших школьников культуры оформления записей в тетрадях по математике кропотливая, требует терпения. Однако необходимо помнить, что эти условности, используемые школьниками, не отражают математической подготовки учащихся, поэтому не следует строго наказывать учащихся за то, что кто-то из них пропустил не 10, а 11 клеток при записи даты или допустил и прочие отклонения. Важно, чтобы записи были рациональными, единообразными, экономичными, лаконичными и при этом эстетично оформленными.

1. Н. Л. Ковалевская, учитель высшей категории, методист высшей категории,

г. Минск//Пачатковае навучанне: сям’я, дзіцячы сад, школа, 2012 г., № 10, стр. 5-12

Видео:Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Решение уравнений в начальной школе

Успешное усвоение правил решения уравнений в начальной школе зависит от того, насколько прочны знания ребенка о компонентах арифметических действий.

Когда мы знакомимся, например, со сложением, обязательно следует объяснить способы нахождения неизвестного компонента (одного из слагаемых).

Развитие умения находить неизвестные компоненты

Для тренировки этого навыка предлагаются выражения с одним отсутствующим слагаемым, вместо
которого используются любые графические знаки ( кружки, квадратики), многоточие или вопросительный знак.

Например, ? + 4 = 7. Как найти неизвестное слагаемое?

По правилам, для этого из суммы следует вычесть известное слагаемое. 7 — 4 = 3. ? = 3

Проверку сложения выполняем вычитанием по этому же правилу::

8 + 2 = 10 Проверка 10 — 8 = 2 10 — 2 = 8

При изучении вычитания нужно обратить внимание на первый компонент выражения — уменьшаемое. Это самое большое число, поэтому, чтобы его найти, следует сложить известные компоненты —
вычитаемое + разность.

Пример ? — 6 = 2 Находим уменьшаемое 6 + 2 = 8. Проверяем правильность нахождения неизвестного компонента. Вместо ? вставляем найденное число 8. 8 — 6 = 2. Уменьшаемое найдено правильно.

Но при нахождении неизвестного второго компонента вычитания (вычитаемого) мы не можем применить сложение известных компонентов. Тогда сумма будет больше уменьшаемого, что недопустимо.

Поэтому, чтобы найти неизвестное вычитаемое, из самого большого числа — уменьшаемого — мы вычитаем разность:

10 — ? = 6 ? = 10 — 6 = 4 ? = 4 Проверяем правильность нахождения вычитаемого 10 — 4 = 6 Вычитаемое найдено верно.

После изучения умножения и деления таким же способом мы учимся находить неизвестные компоненты этих действий.

Компоненты умножения: множитель х множитель = произведение. Если неизвестен один из множителей, мы находим его, разделив произведение на известный множитель.

? х 4 = 8 8 : 4 = 2 Неизвестный множитель = 2 . Проверяем 2 х 4 = 8.

2 х ? = 8 8 : 2 = 4 Неизвестный множитель = 4. Проверяем 2 х 4 = 8. Неизвестные множители найдены верно.

При делении, как и при вычитании, первый компонент ( делимое) — самое большое число. Поэтому, если неизвестен именно он, то делимое находим, перемножив делитель (второй компонент
деления) на частное (результат деления).

? : 3 = 2 3 х 2 = 6 Уменьшаемое = 6. Проверка: 6 : 3 = 2. Уменьшаемое найдено верно.

Но если неизвестен второй компонент деления ( делитель), то для его нахождения применять умножение нельзя.

Для того, чтобы найти неизвестный делитель, следует первый компонент деления
(делимое) разделить на результат (частное)

6 : ? = 2 Находим делитель 6 : 2 = 3. Проверяем 6 : 2 = 3. Делитель найден верно.

Уравнения и их решение

В математике уравнениями называются выражения, в которых неизвестные компоненты обозначены латинской буквой:

x + 5 = 10, 8 — y = 5, a x 3 = 9, 8 : b = 2

Следовательно, выражения 3 + 5 = 8 , 10 — 6

Видео:Простые уравнения. Как решать простые уравнения?Скачать

Начальные классы. Уравнения.

С уравнениями ученики знакомятся в 1 классе. Сначала решают примеры с окошком: выполняют действия с числами и задания на нахождение неизвестного числа, например было равенство:

И одно число решили спрятать:

Нам нужно догадаться, что за число спрятали?
Здесь прекрасно видно, чтобы найти неизвестное число, нужно из 9 — 2
Искомое число – 7.

В нашем равенстве – искомое число называют неизвестным числом.
А равенство, в котором одно число стало неизвестным, называется УРАВНЕНИЕМ.
Никто из вас никогда не видел, чтобы уравнения делали с «окошком». Это неудобно. Гораздо проще неизвестное обозначать буквами.

Неизвестное число обозначают маленькими латинскими буквами

или любой другой буквой.

И этому числу дают имя – корень уравнения.
Давайте посмотрим записи:
8+х
8+х>5
8+х =10
Только третья запись — уравнение. Потому что здесь есть неизвестное число и знак =.
Нам необходимо узнать это число.
Найти все значения х, при котором равенство будет верным — значит, решить уравнение, т.е. найти его корень.

При решении уравнения учитываем взаимосвязи между целым и частью:
— чтобы найти целое, надо сложить части;
— чтобы найти часть, надо из целого вычесть другую часть.

Если вы хотите более подробно узнать, как связаны целое и части, читайте тут.

Решение записывается так:

Корень пишем на следующей строке и подчеркиваем прямой линией.

Корень уравнения = 7, следовательно, наше уравнение решено.
Нам обязательно нужно проверить правильно мы нашли корень уравнения или нет.
Уравнение без проверки – это не уравнение.
Итак, в нашем уравнении корень –7, мы его подчеркнули, а теперь сделаем проверку. Для этого мы переписываем первую строку уравнения, но вместо неизвестного поставим значение корня.
Теперь: знак = пишем под знаком =. Число, записанное справа от знака равно: 9 – переписываем. Выражение, которое находится слева от знака равно: 7 + 2 – считаем. Получится 9. Это число 9 записываем слева от знака =.
Читаем выражение: 9 = 9. Значит, уравнение решили правильно.

Решим еще одно уравнение:

Ученикам начальной школы нужно обязательно овладеть математической речью. Для этого нужно знать, как называются компоненты при различных действиях, и как находится неизвестный компонент:

Если из суммы вычесть одно из слагаемых, то получится другое слагаемое.
Если к разности прибавить вычитаемое, то получится уменьшаемое.
Если из уменьшаемого вычесть разность, то получится вычитаемое.

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 5 / 5. Количество оценок: 66

📺 Видео

КАК РЕШАТЬ УРАВНЕНИЯ ЛЕГКО / ПРОСТОЕ ОБЪЯСНЕНИЕ / уравнение начальная школа #простыеуравненияСкачать

РЕШЕНИЕ УРАВНЕНИЙ |ПОДРОБНОЕ ОБЪЯСНЕНИЕ КАК РЕШИТЬ УРАВНЕНИЯ / ПРОСТЫЕ УРАВНЕНИЯ 2 КЛАСС МАТЕМАТИКАСкачать

РЕШЕНИЕ УРАВНЕНИЙ ЛЕГКО ! 1 КЛАСС МАТЕМАТИКА УРАВНЕНИЯ - ПЕТЕРСОН / ОБЪЯСНЕНИЕ КАК РЕШАТЬ УРАВНЕНИЯСкачать

Оформление тетради по математике. Как оформить классную и домашнюю работу по математике?Скачать

Как научить ребёнка решать уравнения без ошибокСкачать

Математика в начальной школе: основы решения уравненийСкачать

Как решают уравнения в России и СШАСкачать

Решение уравнений в начальной школеСкачать

УРАВНЕНИЕ 4 КЛАСС МАТЕМАТИКА УЧИМСЯ РЕШАТЬ УРАВНЕНИЯ МЕТОДИКА ОБУЧЕНИЯ РЕШАЕМ УРАВНЕНИЯ #уравнениеСкачать

Сложные уравнения. Как решить сложное уравнение?Скачать

Простые уравнения. Легко объясним детям, как решать уравнения. 1 класс.Скачать

Как сделать урок математики интересным? Урок математики в начальной школе. Школа молодого учителяСкачать

Начальная школа. Лысенкова С.Н. Формулы вычисления Р и S. Решение уравненийСкачать

Решение простых уравнений. Как решать уравнения в 5 классе, не зная правил. План решения уравнений.Скачать

Простые уравнения на умножение и деление. Легко объясняем детям, как решать уравнения.Скачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать